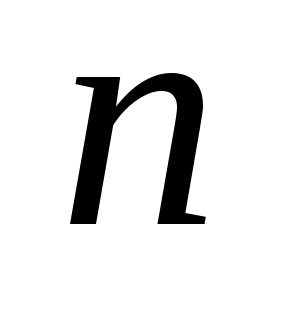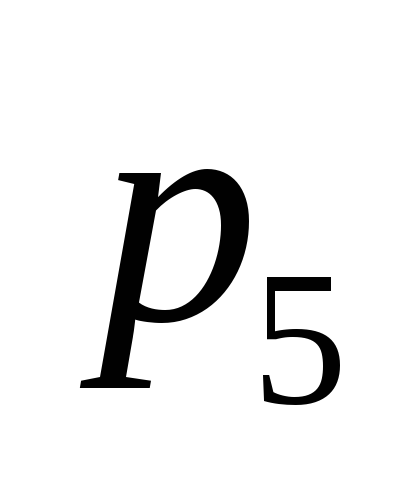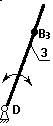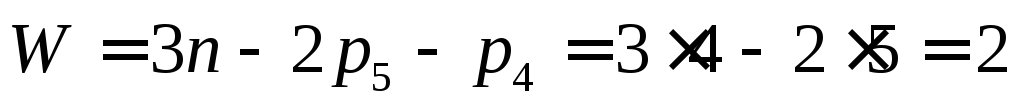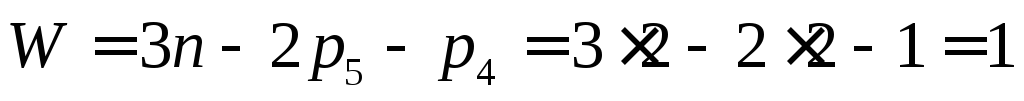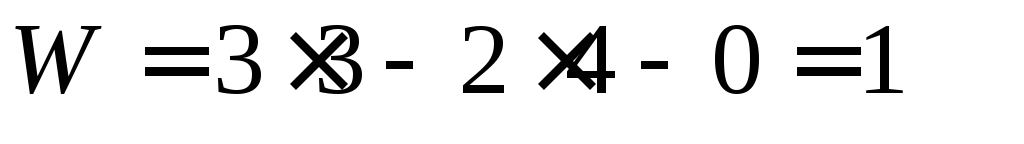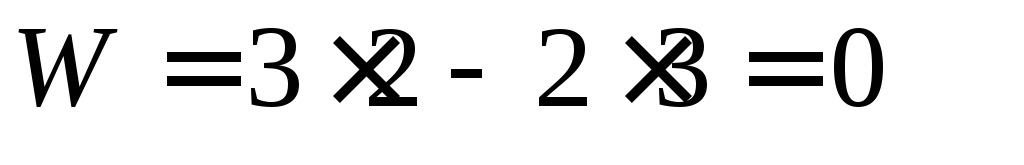Как сделать структурный анализ механизма
Как сделать структурный анализ механизма
Кинематические пары (КП) классифицируются по следующим признакам:
Классификация КП по числу подвижностей и по числу связей приведена в таблице 2.1.
Классификация кинематических пар по числу связей и по подвижности.
| Класс пары | Число связей | Подвижность | Пространственная схема (пример) | Условные обозначения |
| I | 1 | 5 | ||
| II | 2 | 4 | ||
| III | 3 | 3 | ||
| IV | 4 | 2 | ||
| V | 5 | 2 |
Примечание: Стрелки у координатных осей показывают возможные угловые и линейные относительные перемещения звеньев. Если стрелка перечеркнута, то данное движение в КП запрещено (т.е. на данное относительное движение наложена связь).
Понятие о структурном синтезе и анализе.
Основные понятия структурного синтеза и анализа.
Основные структурные формулы.
Для расчета избыточных связей, согласно второму определению, используется следующая зависимость:
Пример структурного анализа механизма.
Функциональная схема на уровне типовых механизмов.
т. е. как пространственный данный механизм не имеет подвижности, так как число связей в нем существенно (на пять) превышает суммарную подвижность всех его звеньев. Однако от рассмотренного ранее плоского варианта пространственный механизм ничем не отличается, то есть он имеет две подвижности основную и местную. Как отмечено, выше связи, не изменяющие подвижности механизма, являются пассивными или избыточными. Для нашего механизма чилсло избыточных связей:
Структурная классификация механизмов по Ассуру Л.В.
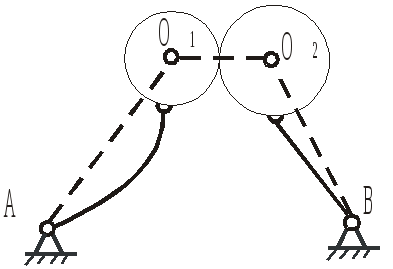
Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура (см. рис. 2.6).
Под первичным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной W пм =1 или несколькими W пм = 1 подвижностями. Примеры первичных механизмов даны на рис. 2.7.
Структурной группой Ассура (или гуппой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю ( W гр = 0).
| Класс и порядок по Ассуру | 1 кл. 2 пор. | 1 кл. 3 пор. | |
| Число звеньев группы n гр | 2 | 4 | и т. д. |
| Число кинематических пар p 1 | 3 | 6 | |
| Класс и порядок по Артоболевскому | 2 кл. 2 пор. | 3 кл. 3 пор. |
Дальнейшее развитие эта структурная классификация получила в работе [6], где была распространена на механизмы с высшими кинематическими парами.
| группа звеньев 5-6 |
| группа звеньев 3-4 |
| группа звеньев 7-8 звено 2 |
| Рис. 2.9 |
После таких изменений классов КП подвижность механизма
Контрольные вопросы к лекции 2.
Структурный анализ механизма.
Основные виды рычажных механизмов.
1. Кривошипно-ползунный механизм.
а) центральный (рис.1);
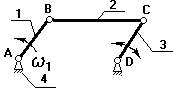
б) внеосный (дезоксиальный) (рис.2);
Рис. 2
1-кривошип, т.к. звено совершает полный оборот вокруг своей оси;
2-шатун, не связан со стойкой, совершает плоское движение;
3-ползун (поршень), совершает поступательное движение;
 |
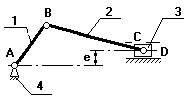
2. Четырехшарнирный механизм.
Звенья 1,3 могут быть кривошипами.
Если зв.1,3 – кривошипы, то механизм двукривошипный.
Если зв.1 – кривошип (совершает полный оборот), а зв.3 – коромысло (совершает неполный оборот), то механизм кривошипно-коромысловый.
Если зв.1,3 – коромысла, то механизм двукоромысловый.
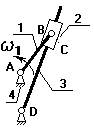
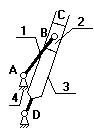
3. Кулисный механизм.
 |
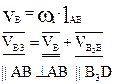 |
на зв.3 выбирают точку В3 и выбирают в данный момент так, чтобы она совпадала с точкой В.
(в кинематическом отношении подобен кулисному механизму).
 |
В процессе проектирования конструктор решает две задачи:
· анализа (исследует готовый механизм);
· синтеза (проектируется новый механизм по требуемым параметрам);
Анализ рычажных механизмов.
В данной главе будут рассмотрены вопросы:
1. структурный анализ механизма (изучение строения механизма);
2. изучение классов и видов кинематических пар.
3. определение числа степеней свободы механизма и определение наличия или отсутствия избыточных связей; в случае наличия – дать рекомендации по способу их устранения;
4. кинематический анализ механизма.
Структурный анализ механизма.
Примечание:
Кинематическая пара существует, если не происходит деформации звеньев, образующих эту пару, и не должно происходить отрыва звеньев одно от другого, образующих кинематическую пару.
Примечание:
Ограничения, накладываемые на независимые движения звеньев, образующих кинематическую пару, называются – условия связи S.
Число степеней свободы механизма
где Н – подвижность.
Любое незакрепленное тело в пространстве имеет 6 степеней свободы, на плоскости – 3.
Классификация кинематических пар проводят либо числу связей, либо по числу подвижностей:
Число связей Класс КП Число подвижностей
S=1 PI H=5
S=2 PII H=4
S=3 PIII H=3
S=4 PIVH=2
S=5 PVH=1
Существует 5 классов кинематических пар.
Примеры различных КП смотри рис. 4-95.
Кинематические пары по характеру контакта звеньев, образующих КП, разделяют на:
Контакт звеньев в низшей КП осуществляется по поверхности. Контакт звеньев в высшей КП – либо по линии, либо в точке.
§1.2 Определение числа степеней свободы рычажных механизмов.
1.2.1 Плоские механизмы.
В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма.
Где n – число подвижных звеньев механизма, рн – число низших КП, рв – число высших КП.
Структурный анализ механизмов
Механизм. Структурная и кинематическая схемы. Масштабные коэффициенты в ТММ. Обобщенная координата. ([1], §6; [2], §2.3)
Структурные формулы для пространственного и плоского механизмов. ([1], §7-8; [2], §2.4)
Замена высших кинематических пар низшими. ([1], §10; [2], §3.5)
Структурные группы Л.В.Ассура. Классификация структурных групп. ([1], §12-13; [2], §2.5)
Принцип образования механизмов. Класс механизма. Формула строения механизма. ([1], §12-13; [2], §2.5)
Порядок структурного анализа. ([1], §12-13; [2], §2.5)
Механизм. Структурная и кинематическая схемы. Масштабные коэффициенты в ТММ. Обобщенная координата.
Используя понятие «кинематическая цепь» можно дать другое определение понятию «механизм».
Механизм – это кинематическая цепь, в которой по заданному положению (или закону движения) относительно стойки одного входного звена (или нескольких входных звеньев) однозначно определяется положение (или закон движения) относительно стойки всех других звеньев [1].
Для изучения структуры или кинематики движения, механизмы изображают в виде абстрактных схем. Эти схемы называют соответственно структурными и кинематическими.
Структурная схема – это условное изображение механизма в виде кинематической цепи с использованием общепринятых обозначений звеньев и кинематических пар. Структурная схема строится без учета масштаба. Она показывает, из каких звеньев состоит механизм (входное, выходное, промежуточные) и определяет последовательность и способ их соединения. Структурная схема задается при структурном анализе и является целью структурного синтеза механизма. Структурную схему часто еще называют принципиальной [2].
Кинематическая схема – условное изображение механизма с использованием стандартных обозначений звеньев и кинематических пар, выполненное с учетом реальных пропорций механизма, т.е. в масштабе. Используется для кинематического исследования механизма (определения положений звеньев, определения перемещений отдельных точек и звеньев, траекторий движения точек, их скоростей, ускорений, угловых скоростей и угловых ускорений звеньев).
На рис.2.1 изображены примеры структурных схем простых плоских механизмов: кривошипно-ползунного (а), кривошипно-коромыслового (б) и криво- шипно-кулисного (в). Не трудно догадаться, что механизмы названы по названиям входного и выходного звеньев.
2 – кулисный камень;
Масштабы и масштабные коэффициенты.
При использовании графических методов решения задач ТММ, физические величины изображают на чертеже в виде отрезков той или иной длины. Для этого используется понятия «масштаба» или «масштабного коэффициента» изображения физической величины. Эти понятия не тождественны, как может показаться на первый взгляд. Кроме того, они не похожи на масштабы географических карт, генеральных планов предприятий и т.д.
Масштаб в ТММ показывает длину отрезка в мм, изображающую единицу физической величины [3]. Масштабным коэффициентом физической величины называют величину, обратную масштабу.
Масштабный коэффициент определяется отношением числового значения физической величины в свойственных ей единицах к длине отрезка в мм, изображающего эту величину. Отсюда получают ту или иную размерность масштабных коэффициентов.
Приведем несколько примеров масштабных коэффициентов, указав их характерные размерности:
Понятие масштаба физической величины используется в ТММ не так часто. Гораздо чаще имеют дело с масштабными коэффициентами.
Если механизм имеет одну степень подвижности, то для определения положения всех его звеньев (при известной их форме и размерах) достаточно знать положение относительно стойки одного звена. Угловую или линейную координату положения этого звена называют обобщенной координатой для всего механизма.
Обобщенная координата – это независимая координата (линейная или угловая), определяющая положение относительно стойки одного из звеньев механизма и позволяющая определить положение (относительно стойки) всех других звеньев. Для кинематического исследования механизму присваивают одну или несколько обобщенных координат. Число обобщенных координат для конкретного механизма определяется числом его степеней подвижности.
Звено, которому приписывается обобщенная координата, называют начальным. Часто за начальное принимают входное звено механизма. В то же время, если это удобно для последующего анализа механизма, за начальное может быть принято выходное звено или одно из промежуточных.
Если механизм имеет несколько степеней подвижности – назначается несколько начальных звеньев и соответствующих им обобщенных координат.
Структурные формулы для пространственного и плоского механизмов.
Структурная формула – это формула, по которой определяется степень подвижности механизма в зависимости от числа подвижных звеньев и количества и вида кинематических пар.
Для вывода структурной формулы пространственного механизма рассмотрим механизм с 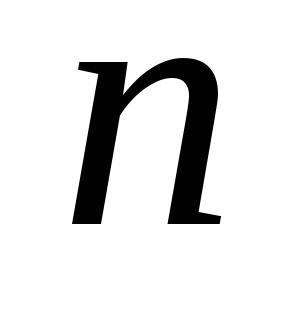
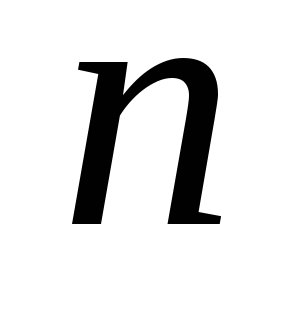
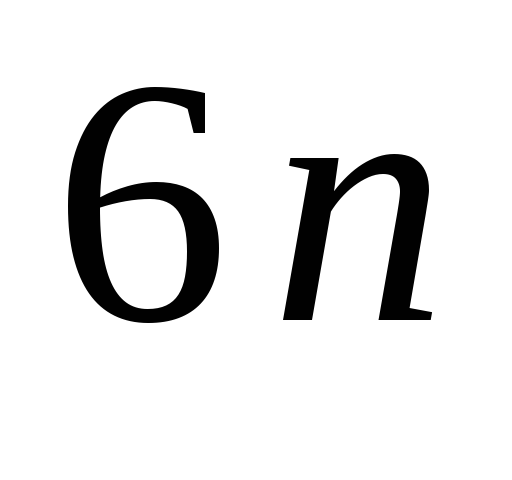
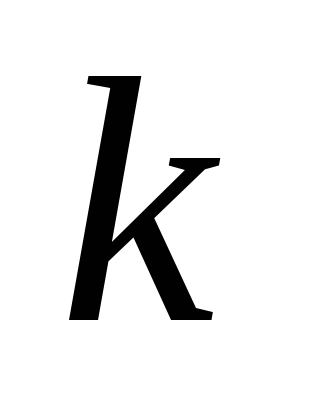
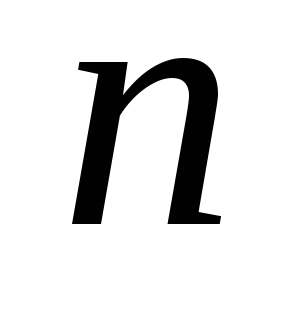
— кинематических пар 5 класса ………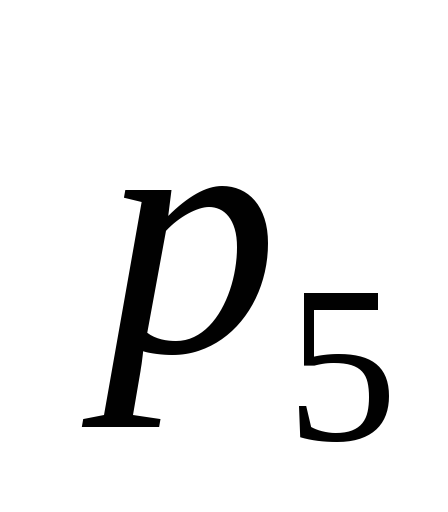
— кинематических пар 4 класса ………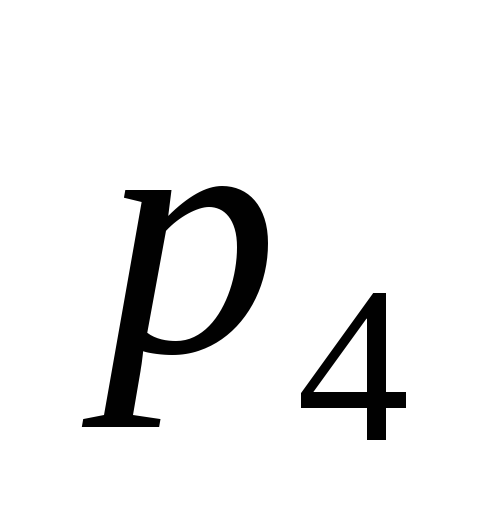
— кинематических пар 3 класса ………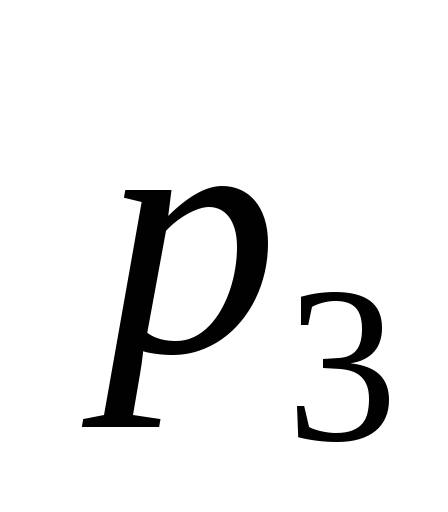
— кинематических пар 2 класса ………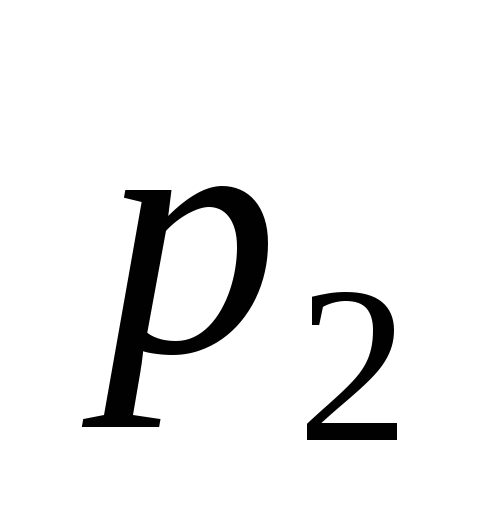
— кинематических пар 1 класса ………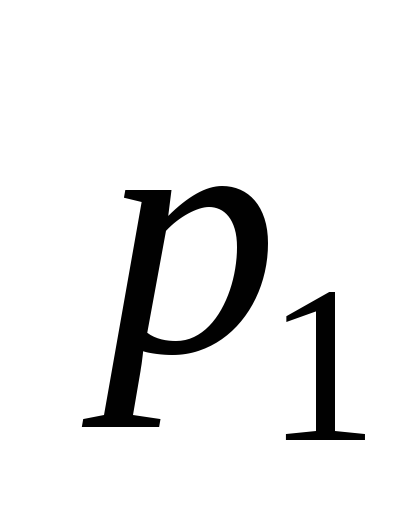
имеет степень подвижности, определяемую выражением (2.1):
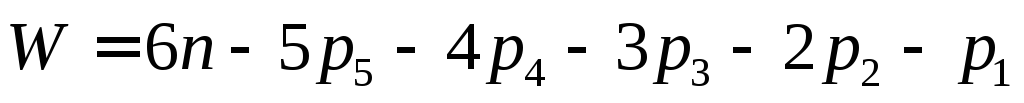
Применив аналогичные рассуждения для плоского механизма, и учитывая число степеней свободы в плоскости (не более 3), получим структурную формулу П.Л.Чебышева 1 для плоских механизмов 2 :
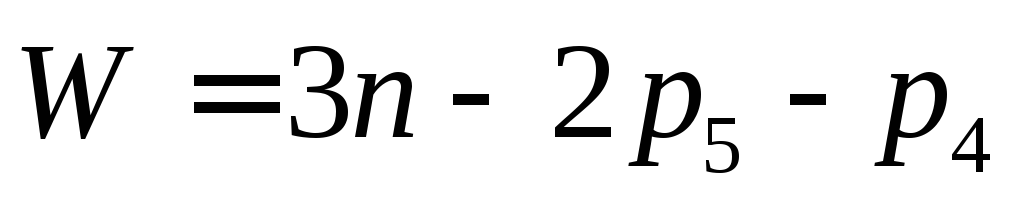
Для плоских механизмов с поступательными парами структурную формулу можно получить из (2.2), уменьшив степени подвижности каждого из слагаемых на единицу (в механизмах с поступательными парами отсутствует поворот звеньев).
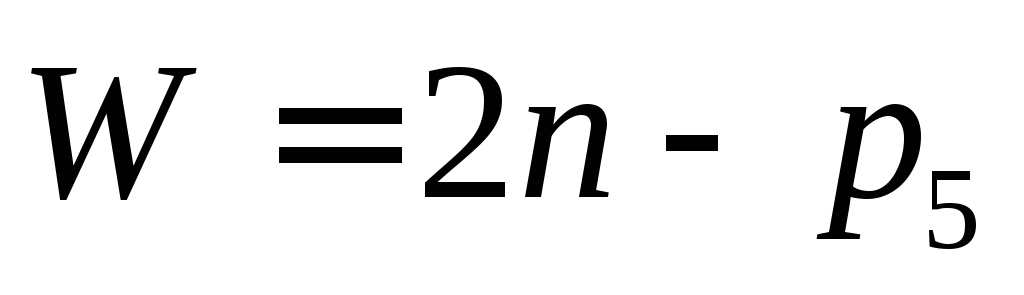
Эта формула предложена В.В.Добровольским в 1937 г. и носит его имя.
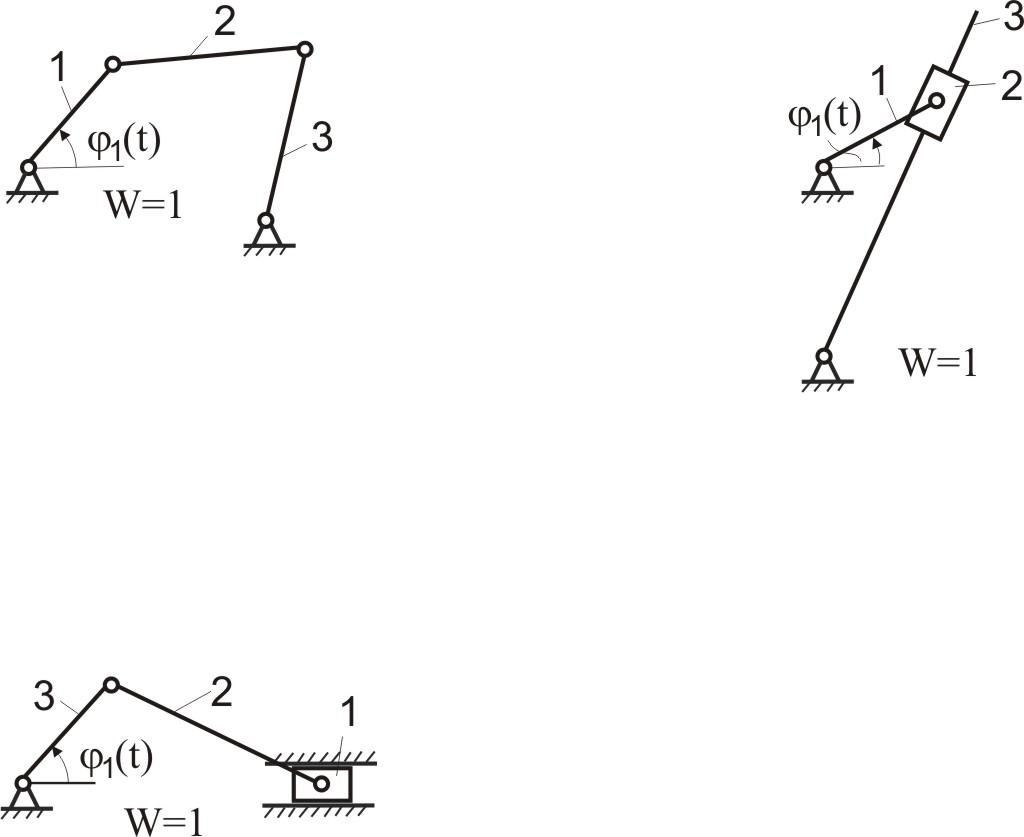
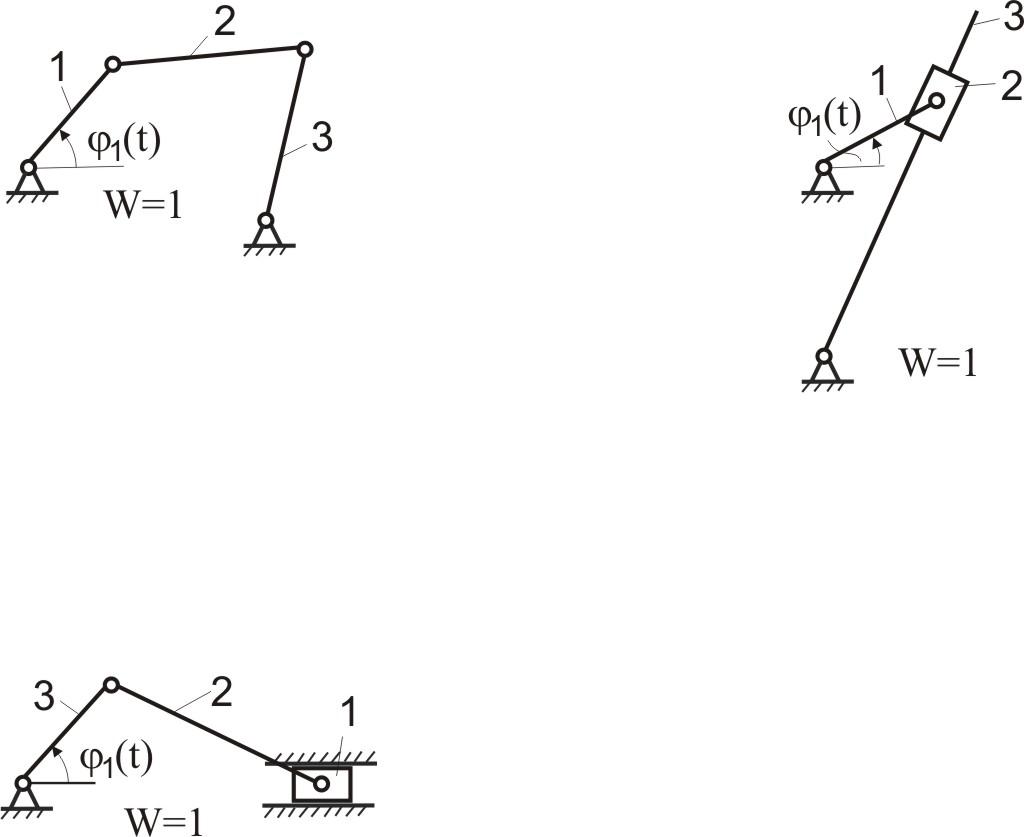
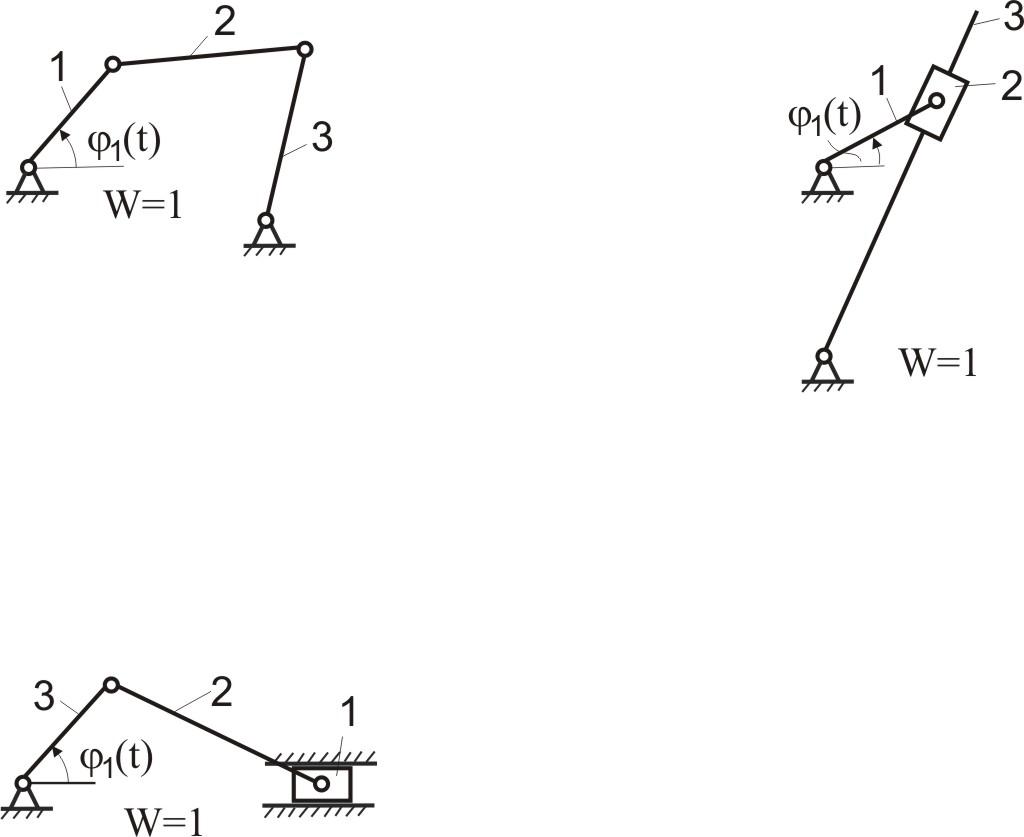
Для примера и закрепления материала, определим степень подвижности плоского механизма, изображенного на рис.2.2.
П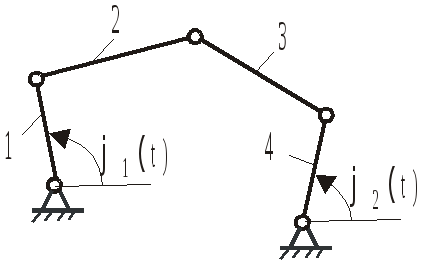
Таким образом, однозначное движение ведомых звеньев 2 и 3 можно получить, введя две обобщенные координаты (т.е. задавая движение двум начальным звеньям 1 и 4 ).
Степень подвижности плоских механизмов, показанных на рис.2.1, предлагаем определить самостоятельно.
Замена высших кинематических пар низшими.
В плоских механизмах, содержащих кинематические пары 4-го класса, для структурной классификации и кинематического исследования целесообразно заменять высшие пары низшими. 1
Замена пар является корректной, если после замены исходного механизма заменяющим степень подвижности и кинематика движения характерных точек в заменяемом и заменяющем механизмах становятся одинаковыми.
Определим степень подвижности этого механизма по формуле Чебышева:
Несмотря на то, что механизм достаточно простой, кинематика движения его звеньев выглядит не вполне понятной. Причиной тому является наличие двухподвижной пары 4-го класса.
Преобразуем механизм в кинематически эквивалентный заменяющий. Учитывая, что расстояния 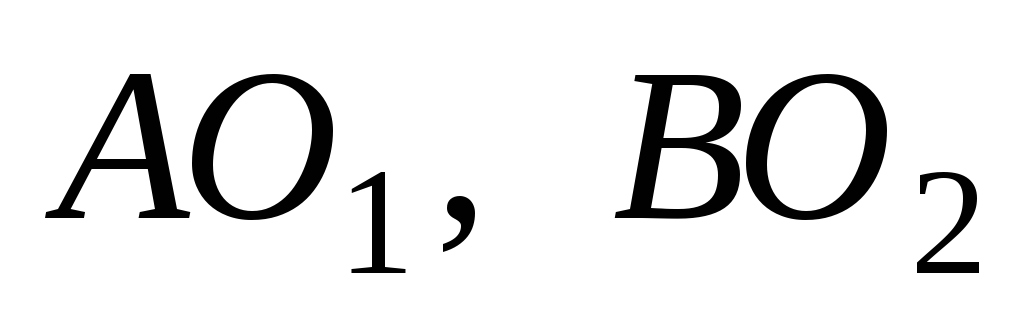
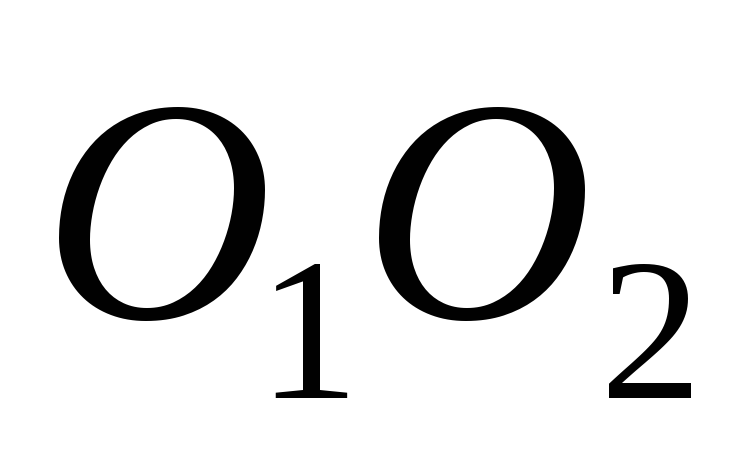
Рис.2.3 можно заменить кинематической цепью 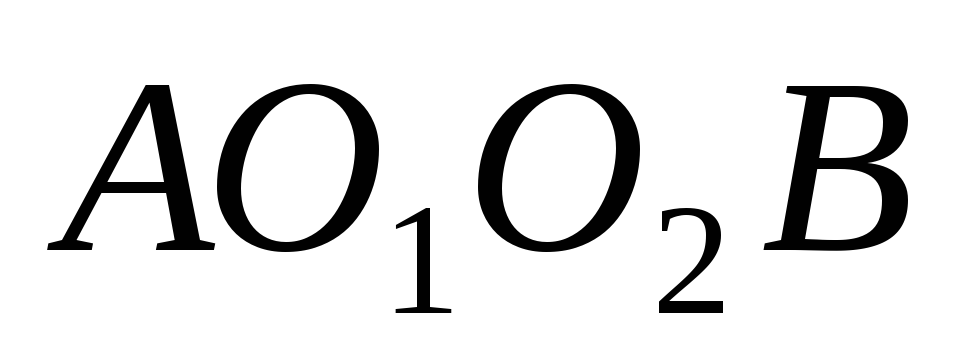
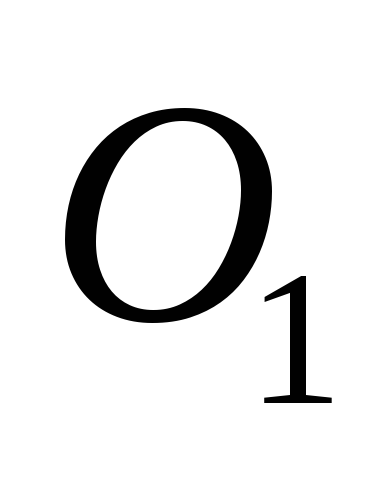
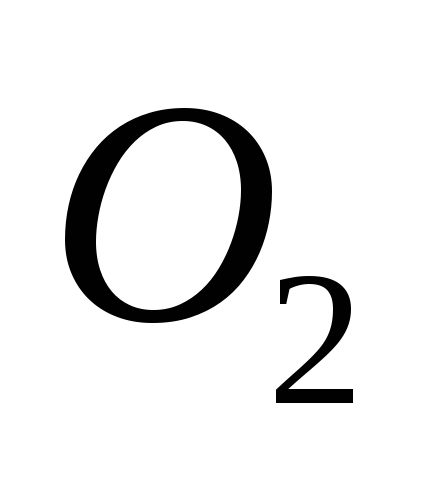
Н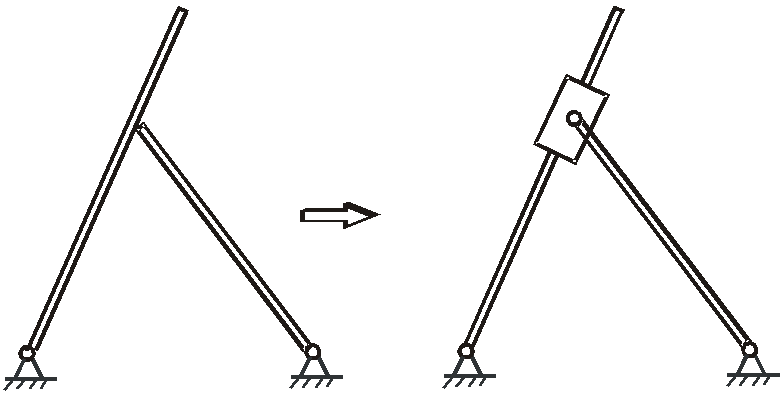
Таким образом, любой плоский механизм, содержащий кинематические пары 4-го класса может быть заменен на кинематически эквивалентный заменяющий механизм с низшими парами 5-го класса. Вид заменяющего механизма определяют по правилам, изложенным в книге [1], §10.
Следует знать, что кинематическая эквивалентность обеспечивается только для конкретных положений заменяемого и заменяющего механизмов. Поэтому такие механизмы еще называют мгновенно кинематически эквивалентными.
Как видно из приведенных примеров, полученный при замене кинематически эквивалентный механизм не является эквивалентным по структуре. Структурные изменения, происходящие в заменяющем механизме, подчиняются закону (2.4):
1 к/п 4-го класса → 2 к/п 5-го класса + 1 звено (2.4)
Структурные группы Л.В.Ассура. Классификация структурных групп
Как было показано в п.2.3, плоский механизм с высшими парами 4-го класса может быть преобразован в кинематически эквивалентный механизм с парами 5-го класса. Структурная формула для заменяющего механизма получит вид:
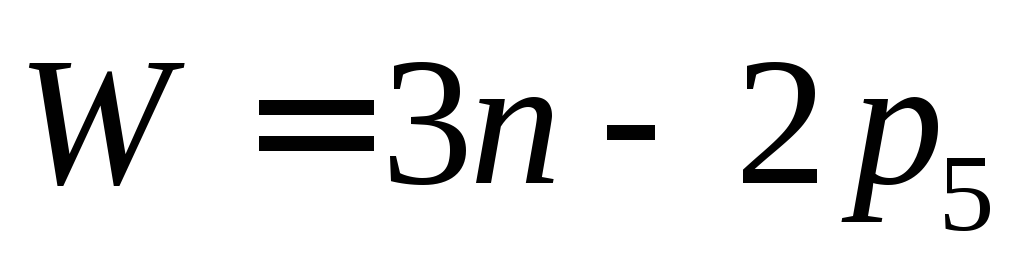
Присутствие в механизме однотипных кинематических пар 5-го класса позволяет создать общую идеологию построения и структурной классификации всех плоских механизмов. Данная задача была выполнена Л.В.Ассуром 1 в классическом труде «Исследование плоских стержневых механизмов с низшими парами с точки зрения их структуры и классификации». 2
Для понимания принципов классификации механизмов введем понятие «структурная группа».
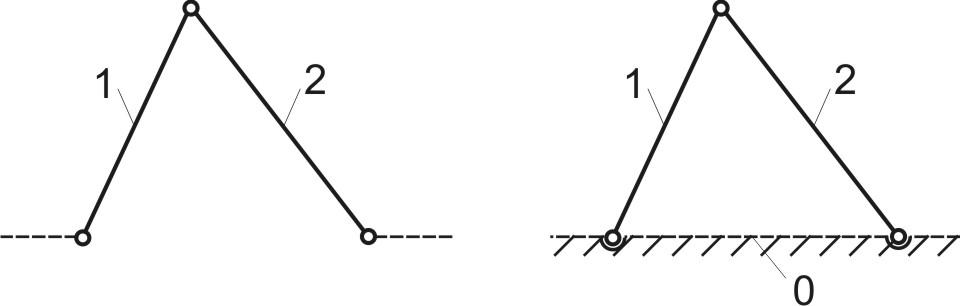
Рассмотрим кинематическую цепь, изображенную на рис.2.5,а. Цепь состоит из звеньев 1 и 2, образующих между собой вращательную кинематическую пару. Эту кинематическую пару будем называть внутренней. Свободными концами звенья входят в кинематические пары с другими звеньями механизма (показаны пунктиром). Эти пары для рассматриваемой цепи будем считать внешними. Все кинематические пары – вращательные пары 5-го класса.
Требуется определить степень подвижности данной кинематической цепи.
Один из способов решения задачи заключается в мысленном присоединении рассматриваемой цепи к механизму с известной степенью подвижности (рекомендуется в 3). Присоединение осуществляется элементами внешних кинематических пар. Степень подвижности вновь образованного механизма должна увеличиться на величину, равную степени подвижности исследуемой цепи звеньев.
Применяя второй из описанных способов, мысленно присоединим исследуемую кинематическую цепь к стойке 0 (Рис.2.5,б) и вычислим степень подвижности полученной замкнутой цепи звеньев по формуле Чебышева:
Результат свидетельствует о том, что при показанном соединении со стойкой кинематическая цепь звеньев 1 и 2, двигаться относительно стойки не может, т.е. обладает относительно нее нулевой степенью подвижности. 3
Структурной группой (группой Ассура) называют кинематическую цепь с нулевой степенью подвижности относительно звеньев, к которым она присоединена, и которая не может быть разделена на более простые кинематические цепи с нулевой степенью подвижности [1, 2].
В литературе можно встретить и другое определение, близкое по своей сути к первому.
Структурной группойназывается кинематическая цепь, присоединение которой к механизму не изменяет число его степеней подвижности, причем группа не должна распадаться на более простые кинематические цепи, удовлетворяющие этому условию [2, 3].
Таким образом, при структурном анализе механизмов и выявлении структурных групп должны быть проверены два условия:
Степень подвижности выделенной кинематической цепи (предположительно – структурной группы) после присоединения к стойке элементами внешних пар должна быть W=0.
Выделенная кинематическая цепь (предположительно – структурная группа) не должна распадаться на более простые цепи с W=0.
Структурной группой (группой Ассура) считают кинематическую цепь, удовлетворяющую обоим условиям одновременно.
Для иллюстрации важности второго условия приведем пример (см. Задачу ниже).
Дано: На рис.2.6,а изображена кинематическая цепь, состоящая из 4-х звеньев.
Требуется: Выяснить, является ли данная цепь структурной группой Ассура?
1. Проверяем степень подвижности цепи. Для этого мысленно присоединим цепь к стойке элементами внешних кинематических пар и применим формулу Чебышева.
Первое условие существования группы Ассура выполнено.
2. Проверяем возможность разделения исследуемой цепи на более простые цепи с W=0.
Такая возможность существует. Исходная цепь может быть разобрана на две цепи с W = 0 (Рис.2.6,б).
Ответ. Исходная кинематическая цепь не является структурной группой.
Для выявления и классификации структурных групп выясним вопрос о вероятных сочетаниях числа звеньев и числа кинематических пар в различных структурных группах. Для этого используем формулу Чебышева для механизмов с парами 5-го класса, подставив в нее условие W=0.
Получим: 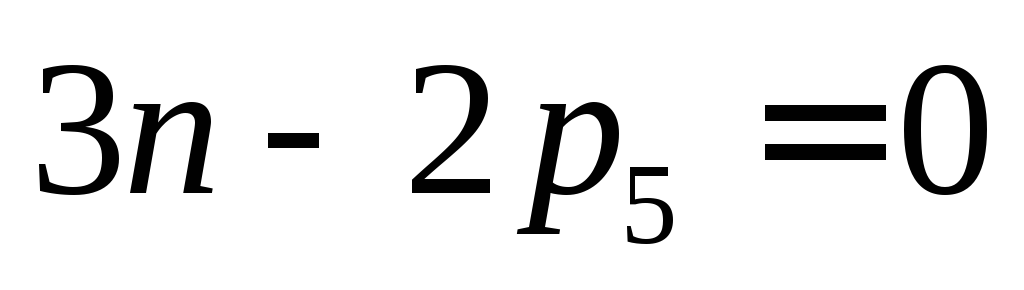
Отсюда следует: 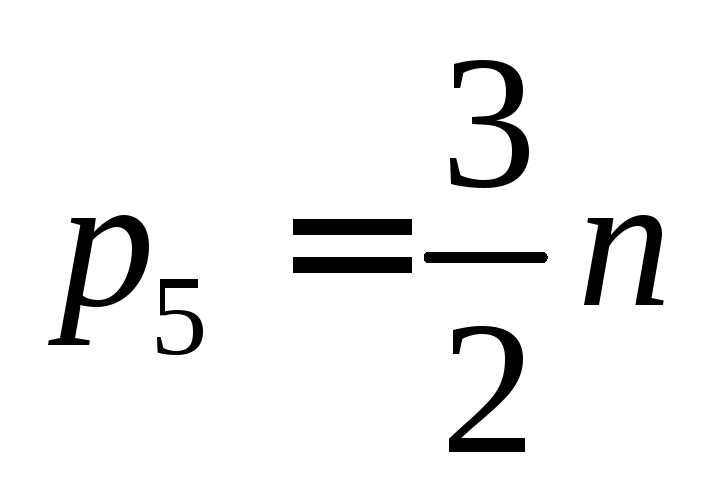
и возможные сочетания