Как сделать ступени пенроуза
На вершину спуска
Существует множество так называемых невозможных фигур, то есть объектов, существование которых кажется недопустимым в трехмерном мире. Однако из-за оптических иллюзий возникает чувство, что они есть на самом деле. Среди них есть и такая интересная математическая загадка, как лестница Пенроуза, которая, казалось бы, не может существовать в реальности. Тем не менее, существует множество видео в интернете, подтверждающих существование невозможных фигур.
Лестница Пенроуза — одна из самых больших загадок-иллюзий нашего времени
Невозможная бесконечная лестница
Одной из, пожалуй, самых известных фигур является лестница Пенроуза. Лайонел и Роджер Пенроузы не открыли эту удивительную модель, но разработали её образец, если можно так выразиться, проект, отображённый на бумаге, воплотив в жизнь идею Оскара Рутерсварда. Являясь одной из пространственно-математических загадок, лестница, выдуманная Пенроузами и Рутерсвардом, до сих пор будоражит умы, заставляя нестандартно мыслящих людей снова и снова пытаться открывать новые грани этого феномена на практике. Модель была впервые опубликована в известном журнале в середине двадцатого века и в скором времени завоевала сердца людей. Ее упоминание можно найти в различных головоломках, играх и даже учебниках психологии. Воздействие подобных загадок на разум человека может быть непредсказуемо.
Кто-то, увидев лестницу без начала и конца, просто восхитится мощью человеческой мысли, кто-то ощутит озарение и создаст шедевр, а кому-то такое просвещение будет только во вред и отрицательно скажется на эмоционально-психологическом состоянии, вызвав помрачение рассудка.
В чем же заключается идея самой лестницы?
Идея проста. При движении объекта по часовой стрелке будет происходить постоянный подъем вверх, а при перемещении в другую сторону – спуск. Самое необычное в том, что после определенного времени движения, объект окажется в той же точке, с которой и начинал путь.
Водопад Эшера — еще одна сложная загадка для пытливых умов
Некоторые люди видят в этом сооружении глубокий философский подтекст, выражающийся в бесконечных попытках убежать от предначертанной судьбы. Нельзя отрицать чужие желания внести подтекст в математические загадки, тем более что чем больше изучаешь математику, тем пристальнее наблюдаешь её связь с философией. Строгие и красивые функции заставляют людей задуматься о вечности и смысле жизни.
Лестница без начала и конца – вымысел или реальность?
Лестница, позволяющая бесконечно подниматься, да ещё и в сравнительно ограниченном пространстве – насколько осуществимо такое явление? Если не принимать во внимание некоторые факторы, и учитывать относительность и субъективность человеческих ощущений – вполне возможно соорудить лестницу в реальности. Само собой, бесконечный подъём или спуск – это просто обман чувств, в вертикальном направлении участник движения по этой лестнице перемещаться не будет, но ощущение бесконечного движения вверх или вниз у человека создастся. На чём и основано создание видео на эту тему, в видеоматериалах ещё проще создать иллюзию.
Всё дело в стереотипическом мышлении и нашей готовности обмануться.
В некоторых местах гор Тибета есть аномальные, по слухам, участки, где вода, если пролить её на скалу течёт вверх – это тот же эффект. Мы видим характерную форму ступеней или разломов породы и готовы, несмотря на их небольшой наклон поверить, что поднимаемся хотя на самом деле передвигаемся в горизонтальной плоскости, а иногда и спускаемся вниз.
Есть ли другие фигуры, поражающие человеческое воображение?
Кроме лестницы, спроектированной Пенроузами и многократно повторяемой в рисунках и даже реальных моделях, есть ещё некоторое количество фигур, которые, как кажется на первый взгляд, не имеют права на существование в реальном мире.
Лестница Пенроуза впечатлила одного немецкого художника, по которой он создал эту лестницу
Вот примеры таких фигур:
Далеко не все из них можно также изящно воплотить в жизнь, как бесконечную лестницу, но надежда ещё не потеряна, может быть, гениальное решение задачи находится где-то рядом.
Надеемся, что предоставленная информация была интересна и познавательна. Если вы знаете о невозможных фигурах что-нибудь кроме вышеописанного – милости просим в обсуждение. А вдруг вы именно тот человек, который раскрыл очередную математическую загадку?
Что такое ступени Пенроуза?
Ступени Пенроуза, или по-другому — «вечная лестница», «бесконечная лестница», «непрерывное восхождение» — одна из самых знаменитых базовых невозможных фигур.
Что такое ступени Пенроуза
Их необычная конструкция, которая не имеет ни конца, ни края, была придумана биологом Лейонелем Пенроузом и его сыном-математиком Роджером Пенроузом.
Впервые модель была опубликована в 1958 г., после чего идея бесконечной лестницы получила большую популярность, стала классической невозможной фигурой, а ее основная концепция нашла применение в живописи, архитектуре, психологии. Модель ступеней Пенроуза обрела самую большую популярность по сравнению с остальными нереальными фигурами в сфере компьютерных игр, головоломках, оптических иллюзиях.

А значит, всего через четыре лестничных марша путник оказывается там же, откуда начал движение.
Соответственно, спускаться или подниматься по ступеням Пенроуза можно бесконечно. Многие находят в этом скрытый глубинный смысл, поэтому вечная лестница крайне популярна в психологии и философии.
Что представляют собой ступени Пенроуза
Главный ключ к разгадке парадокса кроется в понимании явления оптических иллюзий. Известно, что оптические иллюзии — это не что иное, как ошибка в визуальном восприятии.

Рассматривая необычный объект, формы которого не вкладываются в стандартное понимание реальности, мозг адаптирует полученную информацию и формирует ощущение целостности там, где ее нет. Другими словами, создает иллюзию.
Характерной чертой всех невозможных фигур является то, что, на первый взгляд, они похожи на обычные объекты, однако при более детальном рассмотрении видны противоречия в соединениях элементов.
Парадокс заключается в том, что невозможные фигуры кажутся нереальными, однако это заблуждение. Невозможные фигуры могут существовать, ведь любой объект, изображенный на бумаге, можно спроектировать в трехмерном пространстве.
Ключевой нюанс в точке обзора: с одного ракурса невозможная фигура будет выглядеть нереально, с другого — этот эффект будет утерян, фигура визуально приобретет более понятные и привычные формы.
В модели лестницы Пенроуза с целью создания визуальной перспективы использован прием крайней асимметрии: два марша состоят из трех ступеней, а другие два — из семи.

Публикация информации с моделью ступеней Пенроуза стала толчком к развитию в живописи направления импоссибилизма и популяризации картин в стиле имп-арта. Это направление искусства основано на изображении невозможных фигур. Изображения в стиле имп-арт выглядят парадоксально, вызывают интерес и желание их расшифровать, поэтому есть опыт применения таких картин во врачебной практике в целях отвлечения пациента от неприятных медицинских процедур.
Идеи невозможных фигур также вдохновляют многих специалистов в сфере архитектуры на необычные конструкции, будоражащие воображение обывателей. Каждому креативному творцу хочется прикоснуться к нереальному и изменить стандартный образ мыслей, выйти за рамки возможного. Так идея бесконечности ступеней Пенроуза стала прообразом знаменитой лестницы «Перезагрузка» в Мюнхене.
Конструкция представляет собой девятиметровую металлическую спиралевидную лестницу с замкнутыми краями, ходить по ступеням которой можно бесконечное количество раз.
В данном видео наглядно продемонстрировано рисование оптической иллюзии «Бесконечная лестница».
Сооружение не несет никакой практической пользы, однако меняет представление о пространстве, является воплощением нереальности в реальность и напоминанием о том, что все невозможное возможно.
Бесконечная лестница Пенроуза и многое другое
Мир способен удивлять нас снова и снова. Существуют явления, которые не поддаются рациональному объяснению, например, оптические иллюзии или непонятные геометрические фигуры. Сколько бы на них человек не смотрел, разум не может объяснить происходящее. Разве может существовать бесконечная лестница или треугольник, у которого все углы равны 90º? Да, может, и авторами этих гениальных идей являются отец и сын Пенроузы. Но начнем с начала.
Невозможные фигуры
Первая фигура получилась случайно. Однажды в 1934 году 19-летний гимназист Оскар Рутерсвард на уроке латинской грамматики откровенно скучал. От нечего делать он чиркал карандашом в учебнике кубы, которые неожиданно сложились в треугольник. Рисунок был необычным, потому как в трехмерном пространстве и перспективе такие геометрические фигуры не существуют.
Оскар Рутерсвард, став художником, нарисует еще 2500 таких изображений, которые будут притягивать внимание и удивлять людей. С этого момента запускается новое направление в искусстве и науке, которое ломает представления о пространстве и экспериментирует с перспективой.
Пенроузы, отец и сын
Через несколько лет в другой стране, другой молодой человек напечатает статью в психологическом журнале о бесконечной лестнице. Он и не подозревал о существовании Оскара Рутерсварда с его невозможными фигурами. Но гениальные идеи витают в воздухе, ожидая своего часа, и вот, рисунок лестницы из журнала станет знаменитым на весь мир, вместе с его авторами Лайонелом и Роджером Пенроузами.
Отец и сын: два гениальных человека, которые избрали целью своей жизни служение науке. Лайонел Пенроуз был генетиком, увлекающимся математикой. А его сын, Роджер Пенроуз, стал математиком, который увлекся физикой. Однако в чем гениальность идеи? Почему до сих пор она вызывает восхищение?
Лестница Пенроуза
Особенность лестницы заключается в том, что она замкнута сама на себе. Словно мир Льюиса Кэрролла с его «Алисой в зазеркалье» стал реальным. Двигаясь в любом направлении, человек оказывается в исходной точке.
Чудеса лестницы Пенроуза на этом не заканчиваются: если идти по часовой стрелке, то будешь постоянно спускаться вниз, неизменно оказываясь на ступеньке, с которой начал. И наоборот, если идти против часовой стрелки, то будешь подниматься все время вверх и вновь оказываться в исходной позиции. Это движение своей бесконечностью вызывает восторг и недоумение: как это происходит? Какова тайна невозможной лестницы?
Как такое возможно?
Как объясняли сами авторы, все дело в особенностях восприятия и мышления человека.
Нет никакой возможности обойти и посмотреть с другой стороны. В этом вся прелесть. Словно сидишь в зрительном зале театра на пятом ряду с краю и видишь сцену с определенной точки. С этого места часть декораций скрыта кулисами, но если пересесть в центр ряда, то видение поменяется.
На этом эффекте построены изображения невозможных фигур. Само название говорит о том, что реальное существование треугольника, у которого все углы равны 90º, невозможно. Но нарисовать такую фигуру можно. Более того, скульптура невозможного треугольника Пенроуза появилась в 1999 году в городе Перт в Австралии. И здесь начинается самое интересное: как существует то, что в принципе существовать не может?
Иллюзия или реальность
Получается так, что фигура считается невозможной только на рисунке или с определенной точки зрения. Это происходит потому, что когда человек смотрит двумя глазами на один объект, то мозг получает два изображения одного предмета и фокусирует в одну картинку. Это значит, что глаза, находясь на определенном расстоянии друг от друга, воспринимают объект с разных точек. Благодаря этому видны разрывы в фигурах, и поэтому они теряют свою загадочность.
На фотографии за фигурой невозможного треугольника стоит зеркало. Мы смотрим на треугольник, и он кажется целым, но зеркало показывает нам реальную картину. Также и с лестницей Пенроуза. Чтобы она существовала в реальности, необходим разрыв в правом углу.
Мир невозможных фигур
Дизайнер Крис Даффи разработал невозможный стул. Для любителей подшутить над гостями лучше не придумаешь. Кажется, будто стул стоит на двух передних ножках, что в принципе нереально. Секрет заключается в тени от стула, которая является прочной основой.
С удовольствием оптическими иллюзиями пользуются не только модельеры и декораторы, но и психологи. Метод обмана восприятия диагностирует многие психологические проблемы. Например, японский психиатр Акиоша Китаока предложил применять оптические иллюзии для диагностики уровня стресса.
Невозможные фигуры, стирая грань между иллюзией и реальностью, показывают наше несовершенное видение мира. Это является важным аспектом для человека, который хочет понять себя и окружающих.
Принципы построения иллюзий
Дональд Е. Симанек (Donald E. Simanek)
Почему иллюзии так интересны? Почему так много художников используют их в своих произведениях? Возможно, потому что они показывают не то, что нарисовано на самом деле.
Все отмечают литографию «Водопад» («Waterfall») Мориса Эшера (Maurits C. Escher). Вода здесь циркулирует бесконечно, после вращения колеса она течет дальше и попадает обратно в исходную точку. Если бы такую конструкцию можно было бы построить, то был бы вечный двигатель! Но при более внимательном рассмотрении картины мы видим, что художник обманывает нас, и любая попытка построить эту конструкцию обречена на неудачу.
Изометрические рисунки
Классическая перспектива эффективна при имитировании действительности в виде «фотографического» изображения. Это представление неполно по нескольким причинам. Оно не позволяет нам видеть сцену с различных точек зрения, приблизиться к нему или рассмотреть объект со всех сторон. Оно не дает нам и эффекта глубины, которую реальный объект имел бы. Эффект глубины возникает из-за того, что наши глаза смотрят на объект с двух разных точек зрения, и наш мозг их совмещает в одно изображение. Плоский рисунок представляет сцену только с одной определенной точки зрения. Примером такого рисунка может быть фотография, сделанная при помощи обычного монокулярного фотоаппарта.
При использовании этого класса иллюзий, рисунок кажется на первый взгляд обычным представлением твердого тела в перспективе. Но при более близком рассмотрении становятся видны внутренние противоречия такого объекта. И становится ясно, что такой объект не может существовать в действительности.
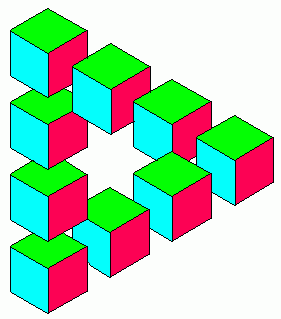
Иллюзия Пенроуза
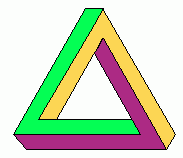
Кажется, что мы видим три бруска квадратного сечения соединенных в треугольник. Если Вы закроете любой угол этой фигуры, то увидите, что все три бруска соединены правильно. Но когда Вы уберете руку с закрытого угла, то станет очевиден обман. Те два бруска, которые соединятся в этом угле, не должны быть даже вблизи друг друга.
В иллюзии Пенроуза используется «ложная перспектива». «Ложная переспектива» используется также и при построении изометрических изображений. Иногда такая перспектива называется китайской (прим. переводчика: Реутерсвард называл такую перспективу японской). Такой способ рисования часто использовался в китайском изобразительном искусстве. При таком способе рисования глубина рисунка двусмысленна.
Фигура Тьери (Thiery) иллюстрирует ту же двойственность.
Иллюзия может быть усилена, если на ней расположить, например, фигуры людей.
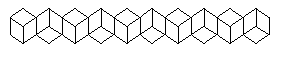
Этот простой рисунок напоминает линию кубиков, показанных то снаружи то изнутри. С другой стороны этот рисунок напоминает линию кубиков, показанных то сверху, то снизу. Но очень трудно воспринять этот рисунок как просто набор параллелограммов.
Закрасим некоторые области черным. Черные параллелограммы могут выглядеть так, как будто мы на них смотрим или снизу или сверху. Попробуйте, если сможете, увидеть эту картину по-другому, как будто на один параллелограмм мы смотрим снизу, а на другой сверху, чередуя их. Большинство людей не может воспринять таким образом эту картину. Почему мы не способны воспринять картину таким образом? Я считаю, что это наиболее сложная из простых иллюзий.
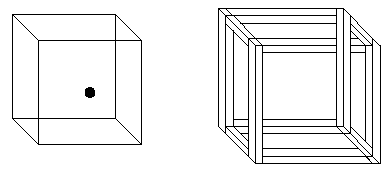
Изометрический рисунок проволочной конструкции куба показывает изометрическую двусмысленность. Эта фигура иногда называется кубом Некера (Necker cube). Если черная точка находится в центре одной сторон куба, то является ли эта сторона лицевой стороной или задней? Вы также можете представить, что точка находится около правого нижнего угла стороны, но вы все равно не сможете сказать, является ли эта сторона лицевой или нет. У вас также не может быть причин предполагать, что точка находится на поверхности куба или внутри него, она с тем же успехом может быть и перед кубом и за ним, так как мы не имеем никакой информации о реальных размерах точки.
Фотографирование иллюзий
Для получения фотографии подобного объекта, необходимо прибегать к различным хитростям. Если используется обычная камера, то наиболее удаленные деревянные блоки захватывают меньший угол обзора, чем ближние блоки. Таким образом наиболее удаленные блоки должны быть изготовлены физически большего размера, чем ближние, а блоки, находящиеся одним краем вблизи, а другим позади должны изготавливаться клиновидными.
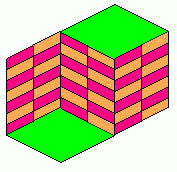
Другой способ применим к фотографированию объектов небольшого размера. Маленькая модель на (см. ниже) сделана из пластиковых брусков Quobo® высотой 1 см. Вся модель имеет размер порядка 7 см. Отметим, что на левом снимке в месте стыковки желтой перекладины с наиболее удаленным красным бруском имеется несоответсвие размеров. Но на правом снимке этой разницы не видно. Отметим также, что на фотографии справа все бруски наклонены под одним и тем же углом, противопложные стороны зеленого основания параллельны, и все остальные линии модели также выглядят параллельными на снимке. Это изометрическая фотография.

На обычной фотографии слева видны кресло и лампа позади модели. Эта фотография была получена при помощи цифрового фотоаппарата с расстояния около 30 см.
Фотография справа была сделана тем же самым фотоаппаратом с такого же расстояния, но с применением телецентрической оптической системы, состоящей из линзы 13 см в диаметре, расположенной таким образом, чтобы ее фокальная точка находилась как можно ближе к линзам фотокамеры. Большая линза была не очень хорошего качества (полученная прессовкой, без шлифовки), поэтому качество фотографии слева хуже. Подобные системы имеют такой недостаток, что пыль, царапины или другие дефекты линзы могут проявиться на финальном изображении. Использование лишь одной линзы вызывает «подушечную» деформацию изображения, при которой изначально прямые линии выглядят немного изогнутыми.
Телецентрические системы высокого качества используются в прозводстве для контроля продукции и в микроскопах для увеличения глубины фокуса. Они ограничены фотографированием объектов меньших диаметра фронтальной поверхности линзы. См. также «Телецентрические системы».
Неоднозначные соединения
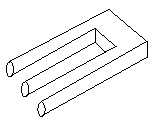
На чем основывается эта иллюзия? Является ли она разновидностью книги Мача?
 Иллюзии положения
Иллюзии положения
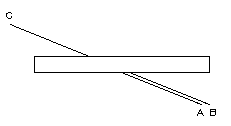
Иллюзия Поггендорфа (Poggendorf), или «пересеченный прямоугольник», вводит нас в заблуждение, какая из линий A или B является продолжением линии C. Однозначный ответ можно дать только, приложив линейку к линии C, и проследив, какая из линий с ней совпадает.
Иллюзии формы
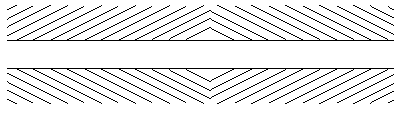
В этих иллюзиях используется особенность нашего мозга обрабатывать видимую информацию, в том числе штрихованные поверхности. Один образец штриховки может доминировать настолько сильно, что другие элементы рисунка кажутся искаженными.
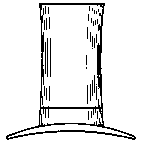
Если круги закрасить черным цветом круги и области, ограничиваемые линиями, то иллюзия будет слабее.
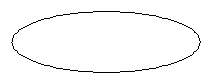
Неоднозначные эллипсы
Наклоненные круги проецируются на плоскость эллипсами, и эти эллипсы имеют двусмысленность глубины. Если фигура (выше) представляет собой наклоненный круг, то не нет способа узнать, находится ли верхняя дуга ближе к нам или дальше от нас, чем нижняя дуга.
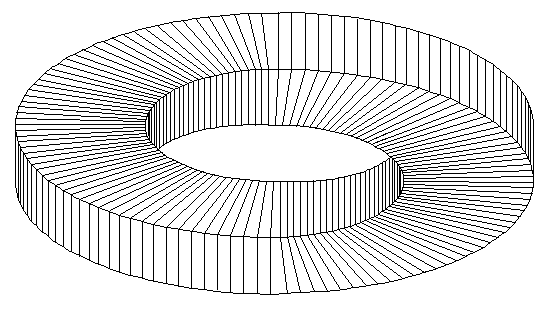
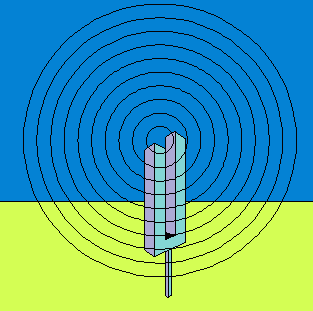
Неоднозначное соединение линий является существенным элементом в иллюзии неоднозначного кольца:
Неоднозначное кольцо, © Дональд Е. Симанек, 1996.

Когда я придумал эту фигуру, я думал, что это она могла бы стать оригинальной иллюзией. Но позже я увидел рекламу с эмблемой корпорации, выпускающей оптоволокно, Canstar. Хотя эмблема Canstar моей, их можно отнести к одному классу иллюзий. Таким образом, я и корпорация разработали независимо друг от друга фигуру невозможного колеса. Думаю, если капнуть глубже, то, вероятно, можно найти и более ранние примеры невозможного колеса.
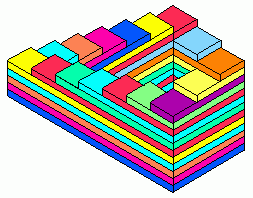
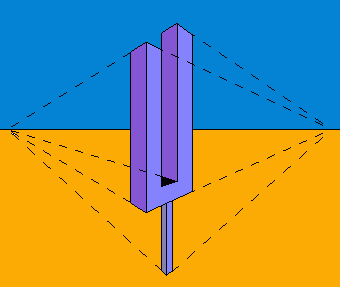
Бесконечная лестница
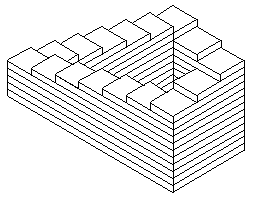
Она также может быть изображена и в перспективе, как это сделано на литографии М. К. Эшера.
Обман на литографии «Восхождение и спуск» строится несколько иным способом. Эшер поместил лестницу на крышу здания и изобразил здание ниже таким образом, чтобы передать впечатление перспективы.
Художник изобразил бесконечную лестницу с тенью. Как и штриховка, тень могла бы уничтожить иллюзию. Но художник поместил источник света в таком месте, что тень хорошо сочетается с другими частями картины. Возможно, тень от лестницы является иллюзией сама по себе.
Заключение
Другие могут увидеть, что с картиной «что-то неправильно», но они и не подумают спросить, каким образом получается обман. У этих людей никогда не возникает потребности понять, как работает природа, они не могут сосредоточиться на деталях за недостатком элементарного интеллектуального любопытства.
Возможно, понимание визуальных парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Среди работ М. К. Эшера (M.C. Escher) есть очень много картин-иллюзий, а также сложных геометрических картин, которые можно отнести скорее к «интеллектуальным математическим играм», чем к искусству. Однако, они производят впечатление на математиков и ученых.
Художники начали использовать геометрическую перспективу в своих работах значительно раньше изобретения фотографии. Но они не могли изучить ее без помощи от науки. Линзы стали общедоступными только в XIV столетии. В то время они использовались в экспериментах с затемненными камерами. Большая линза помещалась в отверстие в стенке затемненной камеры так, чтобы перевернутое изображение отображалось на противоположной стенке. Добавление зеркала позволяло отбрасывать изображение пол потолок камеры. Это устройство часто использовалось художниками, которые экспериментировали с новым «европейским» перспективным стилем в художественном искусстве. К тому времени математика уже была достаточно сложной наукой, чтобы дать теоретическое обоснование перспективы, и эти теоретические принципы были опубликованы в книгах для художников.
Только самостоятельно пробуя рисовать иллюзорные картины можно оценить все тонкости необходимые для создания подобных обманов. Очень часто природа иллюзии накладывает свои ограничения, навязывая свою «логику» художнику. В итоге, создание картины становится сражением остроумия художника со странностями нелогичной иллюзии.
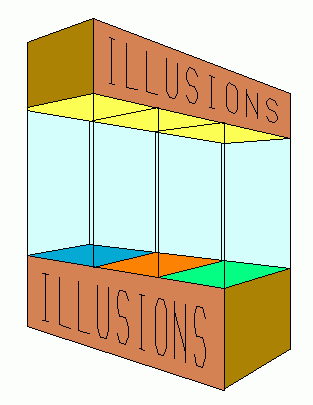
Теперь, когда мы обсудили суть некоторых иллюзий, вы можете использовать их, чтобы создавать собственные иллюзии, а также классифицировать любые иллюзии, которые вам встретятся. Через некоторое время вы будете иметь большую коллекцию иллюзий, и вам необходимо будет каким-то образом демонтрировать их. Я разработал для этого стеклянную витрину.
Витрина иллюзий. © Дональд Е. Симанек, 1996.
Вы можете проверить сходимость линий в перспективе и другие аспекты геометрии этого рисунка. Анализируя такие картины, и пробуя рисовать их, можно узнать суть обманов, используемых в картине. М. К. Эшер (М. C. Escher) использовал подобные уловки в своей картине «Бельведер» (ниже).






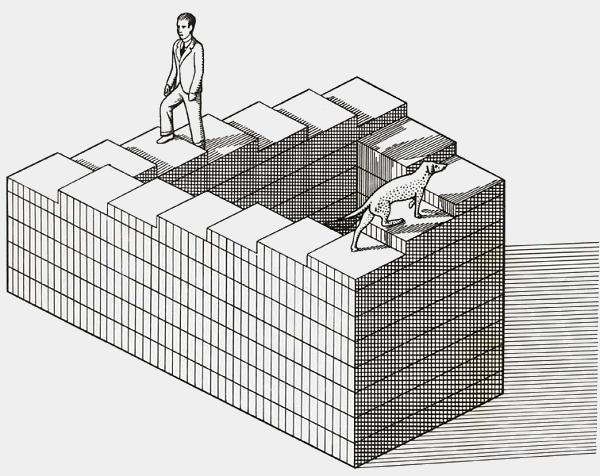





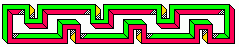



 Иллюзии положения
Иллюзии положения