Как составить таблицу истинности
Как составить таблицу истинности
Как составить таблицу истинности
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
| Переменные | Промежуточные логические формулы | Формула | |||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
2. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
3. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Таблица истинности
Что такое таблицы истинности
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логические выражения
Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».
Их можно разделить на два типа:
Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Унарной в данном случае называется операция, которая используется относительно одной величины.
Конъюнкция
Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
Дизъюнкция
Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
Примеры построения таблицы истинности
Задача
Решение
| А | В | \(А \vee В\) | ¬А | ¬В | \(¬А \vee ¬В\) | \((A \vee B) \wedge (¬A \vee ¬B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)
Решение
| X | Y | Z | ¬ Z | \(Y \wedge ¬Z\) | \(X \vee Y \wedge ¬Z\) |
| 0 | 0 | 0 | q | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.
Построение таблиц истинности
Вы будете перенаправлены на Автор24
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
Готовые работы на аналогичную тему
Решение:
Определим количество строк:
Определим количество столбцов:
Количество логических операций и их последовательность:
Заполним таблицу, учитывая таблицы истинности логических операций.
По данному логическому выражению построить таблицу истинности:
Решение:
Определим количество строк:
Определим количество столбцов:
Количество логических операций и их последовательность:
Заполним таблицу, учитывая таблицу истинности логических операций.
Алгоритм построения логической функции по ее таблице истинности
Решение:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата написания статьи: 12.04.2016
Построение таблиц истинности
В данном методическом пособии предлагаются материалы для самостоятельного изучения правил построения таблиц истинности в алгебре логики студентами заочного отделения. Пособие включает теоретическую часть, примеры и задания.
Просмотр содержимого документа
«Построение таблиц истинности»
Департамент образования Ивановской области
ОГБПОУ «Кинешемский педколледж»
Построение таблиц истинности
Подготовила: Совина М.В.
преподаватель высшей категории
Методическое пособие «Построение таблиц истинности»- Кинешма, 2015
В данном методическом пособии предлагаются материалы для самостоятельного изучения правил построения таблиц истинности в алгебре логики студентами заочного отделения. Пособие включает теоретическую часть, примеры и задания.
Этапы построения таблиц истинности………………………………………
Пример построения таблиц истинности…………………………………….
Логика — это наука о формах и способах мышления. Логика позволяет строить формальные модели окружающего мира.
Первые учения о формах и способах рассуждений возникли
в странах Древнего Востока (Китай, Индия), но в основе
современной логики лежат учения, созданные древнегреческими
мыслителями.
Основными формами мышления являются: понятие, высказывание, умозаключение.
Основы формальной логики заложил Аристотель.
Алгебра логики была разработана для того, чтобы можно было
оперировать высказываниями, не вникая в их содержание.
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй.
Простые высказывания обозначаются латинскими буквами: А, В, С …
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Пусть через А обозначено высказывание “Тимур поедет летом на море”,
а через В — высказывание “Тимур летом отправится в горы”.
А, В — логические переменные, каждое из которых мoжет принимать только два значения — “истина” или “ложь”, обозначаемые, соответственно, “1” или “0”.
Составное высказывание “Тимур летом побывает на море и в горах” можно кратко записать как А и В.
Здесь “и” — логическая связка.
Составное высказывание “Тимур летом побывает на море или в горах” можно кратко записать как А или В.
Здесь “или” — логическая связка.
Истинность или ложность получаемых составных высказываний зависит от истинности или ложности элементарных высказываний.
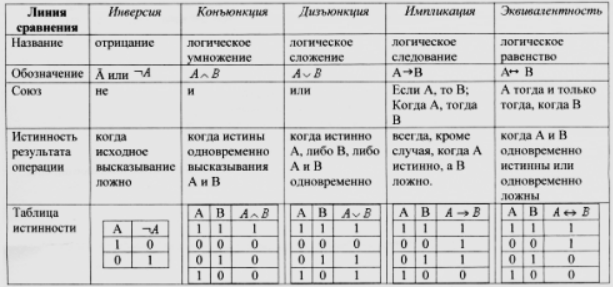
В алгебре логики в соответствии с логическими связками используют 5 базовых логические операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность. Для каждой из операций составлены таблицы истинности
Таблица истинности логической операции выражает соответствие между всевозможными наборами значений исходных данных, переменными и значениями, получаемыми в результате выполнения операции.
Приоритеты логических операций:
конъюнкция (логическое умножение),
дизъюнкция (логическое сложение),
Изменить последовательность выполнения логических операций можно с помощью скобок.
Этапы построения таблиц истинности
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо:
Выяснить количество строк в таблице. Оно равно 2 n +1, где n-количество переменных.
Выяснить количество столбцов. Оно равно количество переменных плюс количество логических операций.
Установить последовательность выполнения логических операций с учетом скобок и приоритетов.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Заполнение столбцов значений переменных таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Заполнение столбцов, содержащих логические операции, выполняется в соответствии с таблицами истинности этих логических операций
Примеры построения таблиц истинности
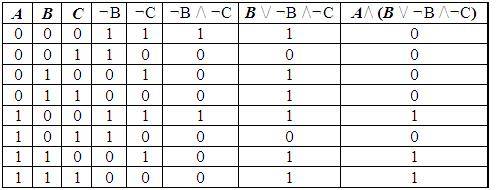
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
1. В выражении две переменные А и В (n=2).
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А
В
А\/ В
¬А
¬В
¬А\/¬В
F
0
1
1
0
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
А
В
С
A\/B
(A\/B) /\ ¬С
0
0
1
0
1
0
1
0
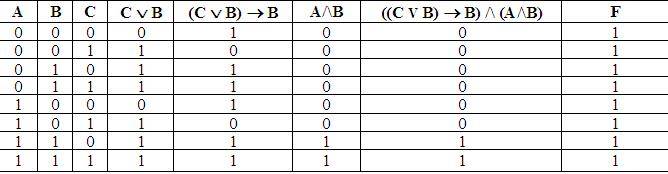
Пример 4. Определите истинность формулы: F = ((С \/В) => В) /\ (А /\ В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
X
Y
Z
F
¬X/\¬Y/\Z
¬X\/¬Y\/Z
X\/Y\/¬Z
X\/Y\/Z
1
1
0
0
1
1
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Информатика
План урока:
Способы решения задач по логике
Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:
Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.
Этапы решения логических задач:
Табличный способ – этапы, особенности
Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.
Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.
Метод таблиц
Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.
Существует общий алгоритм построения таблиц:
Если необходимо перебрать все значения простых выражений, то для задач:
Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.
Обязательно учитывают приоритет операций:
Обозначение логических операций:
Сравнение методов решения
Метод рассуждений
Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.
Пример №1.
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.
Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:
Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:
Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.
Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.
Такой подход лучше не использовать, если условие сложное или много данных.
Табличный метод
Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).
Чтобы построить таблицу истинности логических выражений, следует:
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:
Рассмотрим тот же пример.
Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:
Метод компактнее, для некоторых задач нагляднее.
Построение таблиц истинности для различных типов задач
Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.
Пример 2.
Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.
Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:
А — «Первый студент летал в Англию»;
В — «Второй студент летал в Англию»;
С — «Третий студент летал в Англию».
Запишем выясненные данные при помощи логических операций:
Пример 3.
Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:
По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.
Выясним, какие же классы добились высшего бала.
Разбиваем условие задачи на элементарные высказывания:
А – «А добьется высшего бала»;
В – «В добьется высшего бала»;
С – «С добьется высшего бала».
Запишем логические операции, описанные в примере:
Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.
Пример 4.
Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:
Предложенные имена: Арина, Артур, Кэтрин, София.
Решим задачу, используя таблицу.
Сначала решим пошагово, выполняя операции по приоритету:
Указанному условию соответствует первое имя.
Пример 5.
Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.
Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.
Маша Марина: «Саша заняла второе место, а Света – первое».
Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».
Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».
Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».
Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.
Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором
Рассмотрим все варианты:
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
Рассмотрим этот вид электрической цепочки:
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
Обозначение логических элементов
Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Построено таблиц, форм:
Как пользоваться калькулятором
Видеоинструкция к калькулятору
Используемые символы
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
Что умеет калькулятор
Что такое булева функция
Что такое таблица истинности?
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
| a | b | a ∧ b | a ∨ b | ¬a | ¬b | a → b | a = b | a ⊕ b |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Как задать логическую функцию
Есть множество способов задать булеву функцию:
Рассмотрим некоторые из них:
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬a bc ∨ ¬a ¬b c ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
Алгоритм построения СКНФ для булевой функции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬a b∨ ¬b c∨ca
1. Построим таблицу истинности для функции
| a | b | c | ¬a | ¬a ∧b | ¬b | ¬b ∧c | ¬a ∧b∨ ¬b ∧c | c∧a | ¬a ∧b∨ ¬b ∧c∨c∧a |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: < 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 1 >
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: < 0, 0, 0 > < 1, 0, 0 >
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
| a | b | c | F | 1 | |
| 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 0 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 1 | 1 | 0 | 0 | → | 0 |
| 1 | 1 | 1 | 1 | ⊕ 0 | 1 |
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
| a | b | c | F | 1 | 2 | |
| 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | 1 | → | 1 |
| 1 | 1 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
| a | b | c | F | 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | → | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | ⊕ 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
Окончательно получим такую таблицу:
| a | b | c | F | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Разбор 2 задания ЕГЭ по информатике про таблицы истинности
Объяснение задания 2 ЕГЭ по информатике
2-е задание: «Таблицы истинности»
Уровень сложности — базовый,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
Таблицы истинности и порядок выполнения логических операций
Таблица истинности операции НЕ
Таблица истинности операции И (конъюнкция)
Таблица истинности операции ИЛИ (дизъюнкция)
Таблица истинности операции Импликация (если…, то…)
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
О преобразованиях логических операций читайте здесь.
Решение заданий 2 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- ✎ Способ 2. Программирование:
Язык python:
print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
Язык pascalAbc.net:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
Ответ:
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Результат: ywxz
✎ Способ 2. Программирование:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) false = 0, True = 1
Сопоставив их с исходной таблицей, получим результат: ywxz
print (‘x y z w’) for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y)) F=0 :
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
Результат: cbad
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
✍ Решение:
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln(‘x ‘,’y ‘,’z ‘,’w ‘); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
✍ Решение:
Результат: 31
Подробное объяснение данного задания смотрите на видео:
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
✍ Решение:
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
Результат: 2
Подробное решение задания смотрите в видеоуроке:
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
✍ Решение:
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| . | . | . | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Таблицы истинности
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 19. Таблицы истинности
19.1. Построение таблиц истинности
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
Для того чтобы построить таблицу истинности логического выражения, достаточно:
Пример 1. Построим таблицу истинности для логического выражения
В этом выражении две логические переменные и пять логических операций. Всего в таблице истинности будет пять строк (22 плюс строка заголовков) и 7 столбцов.
Начнём заполнять таблицу истинности с учётом следующего порядка выполнения логических операций: сначала выполняются операции отрицания (в порядке следования), затем операции конъюнкции (в порядке следования), последней выполняется дизъюнкция.

Обратите внимание на последний столбец, содержащий конечный результат. Какой из рассмотренных логических операций он соответствует?
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают.
Таблица истинности, построенная в предыдущем примере, доказывает равносильность выражений
С помощью таблиц истинности докажите равносильность выражений
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
19.2. Анализ таблиц истинности
Рассмотрим несколько примеров.
Пример 2. Известен фрагмент таблицы истинности для логического выражения F, содержащего логические переменные А, В и С.
Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Ответить на поставленный вопрос можно, вычислив значение каждого логического выражения на каждом заданном наборе переменных и сравнив его с имеющимся значением F.
1) Логическое выражение (A v С) & В соответствует данному фрагменту таблицы истинности:
Итак, имеется два логических выражения, соответствующих заданному фрагменту таблицы истинности.
Можно ли утверждать, что в результате решения задачи мы нашли логическое выражение F?
Пример 3. Логическая функция F задаётся выражением:
Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна.
Определим, какому столбцу таблицы истинности функции F соответствует каждая из переменных х, y > z.
В исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (2 3 ) строк.
Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7.
Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110). Построим по этим данным вторую часть таблицы истинности:
Теперь выясним, при каких значениях х, у, z логическое выражение ложно:
Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:
Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, а z может быть и 0, и 1.
Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.
Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, а z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:
САМОЕ ГЛАВНОЕ
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
Истинность логического выражения можно доказать путём построения его таблицы истинности.
Функцию от п переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
Вопросы и задания
1) n = 6, m = 15;
2) n = 7, m = 100;
3) n = 10, m = 500.
4. Рассмотрите два составных высказывания:
• F1 = «Если одно слагаемое делится на 3 и сумма делится на 3, то и другое слагаемое делится на 3»;
• F2 = «Если одно слагаемое делится на 3, а другое слагаемое не делится на 3, то сумма не делится на 3».
Формализуйте эти высказывания, постройте таблицы истинности для каждого из полученных выражений и убедитесь, что результирующие столбцы совпадают.
Какое из приведённых далее логических выражений соответствуют этому фрагменту?
Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F ложна.
Какому столбцу таблицы истинности функции F соответствует каждая из переменных А, В, С?
Как составить таблицу истинности
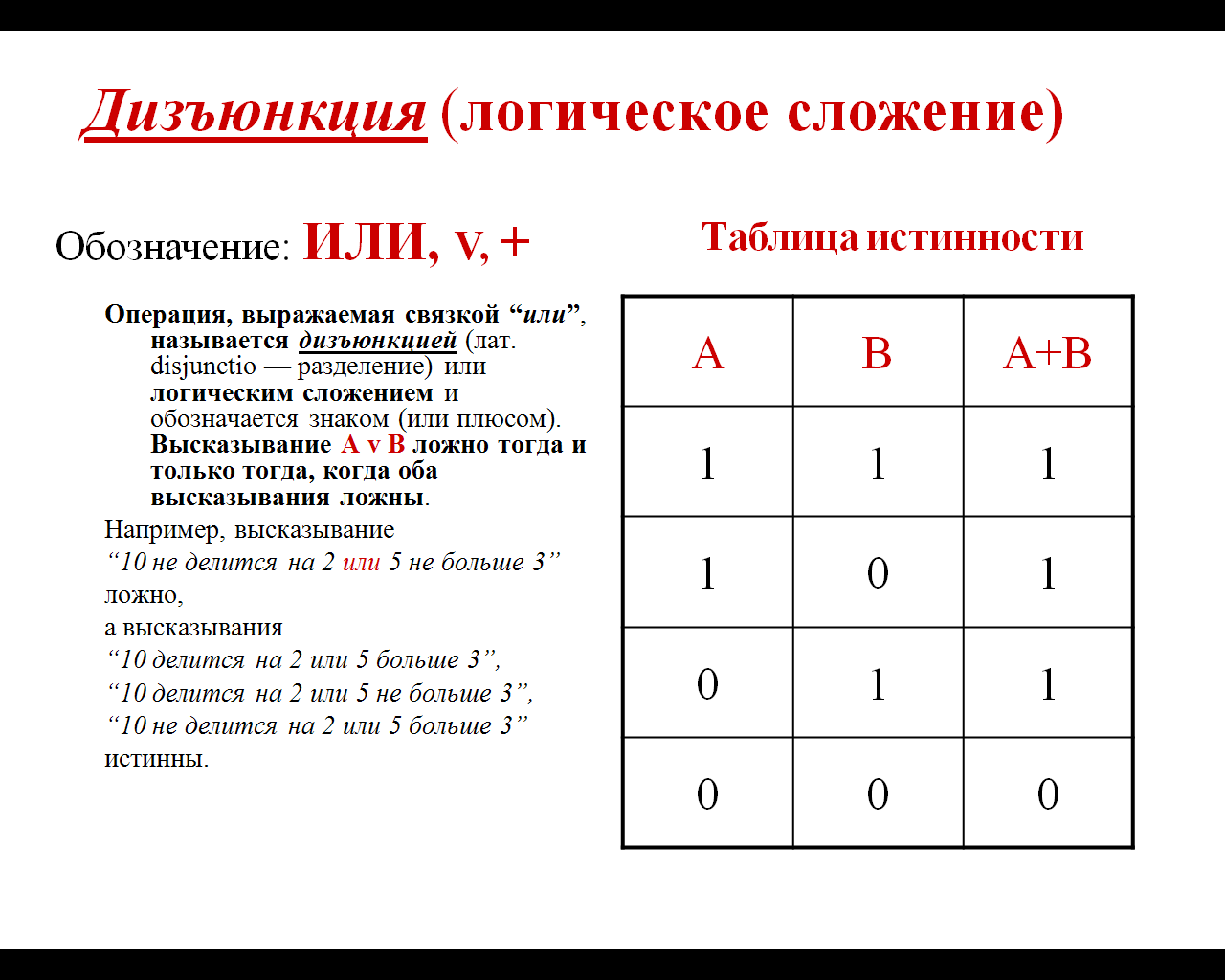
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
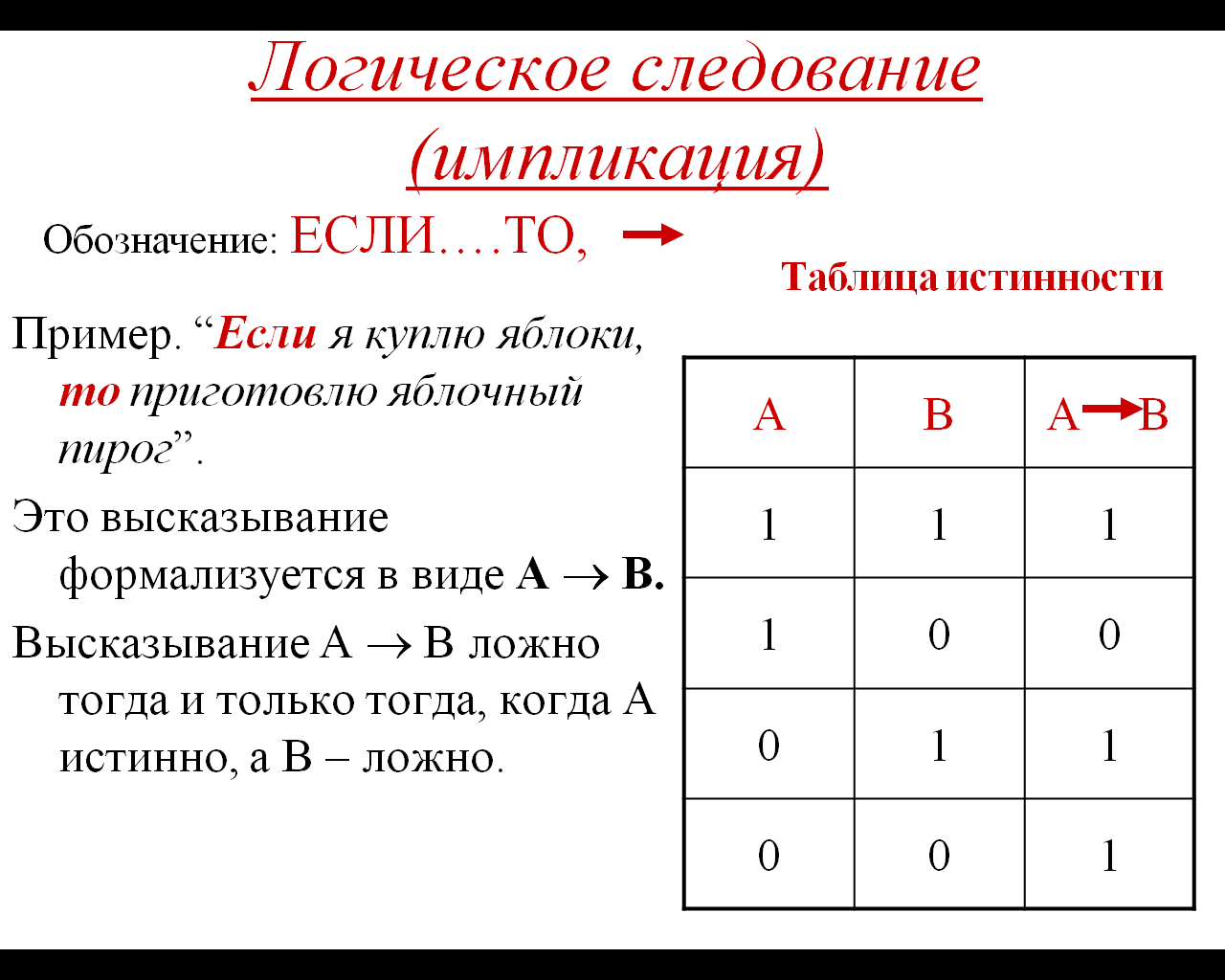
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
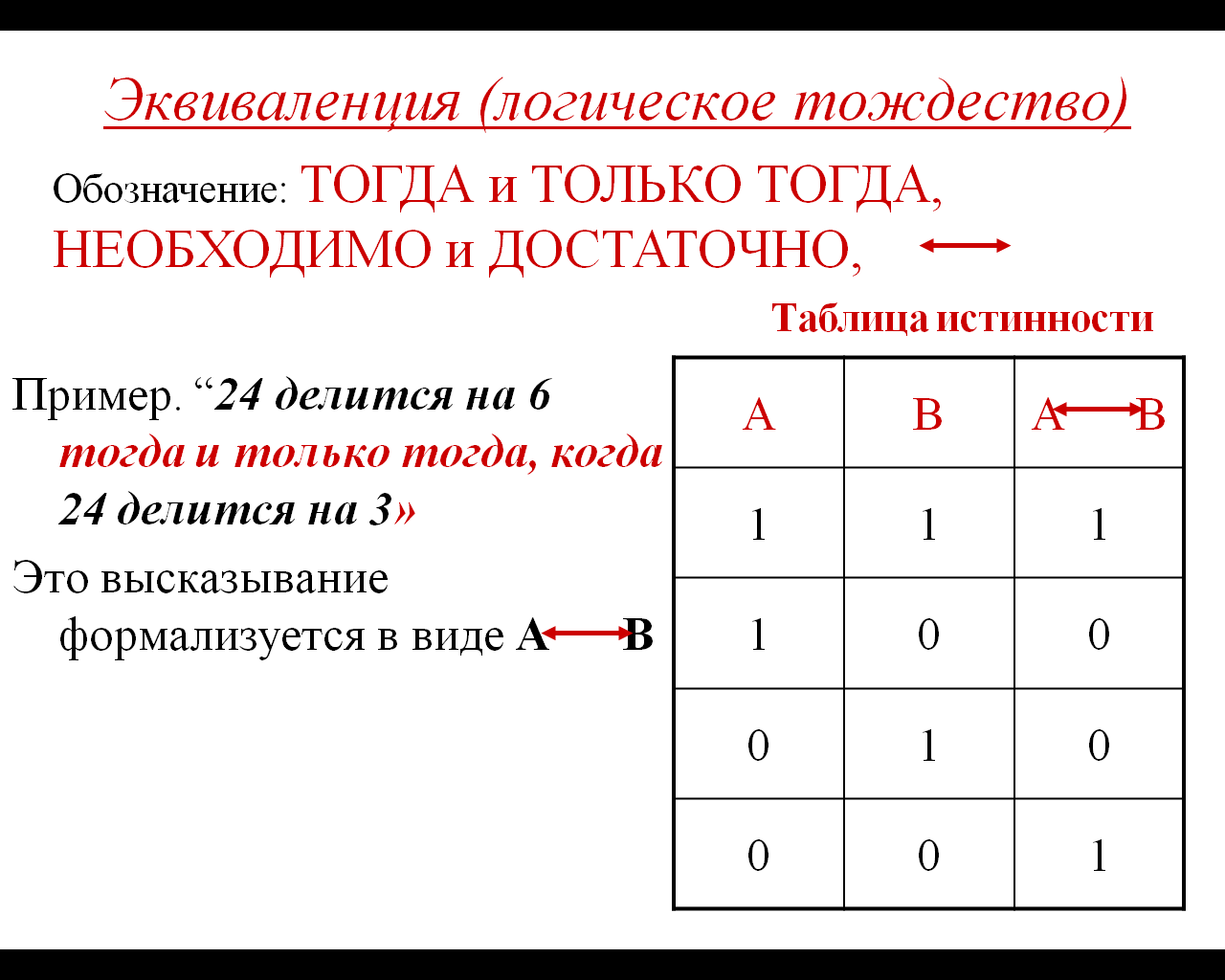
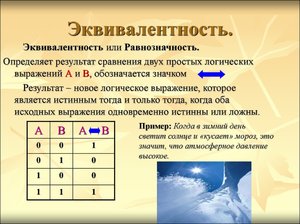
5) Логическая равнозначность или эквивалентность:
5.10. Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0), (0,1), (1,0), (1,1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Примеры.
| Переменные | Промежуточные логические формулы | Формула | |||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Построить таблицу истинности следующих логических выражений
Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.
Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.
Алгебраические преобразования логических выражений
Отрицание
Таблица истинности для отрицания будет такова:
| А | не А |
| Л | И |
| И | Л |
Конъюнкция
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| И | Л | Л |
| И | И | И |
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
Построение таблиц истинности
Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:
В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.
Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:
Примеры
Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:
Штрих Шеффера
| А | Б | А и Б | не (А и Б) |
| Л | Л | Л | И |
| Л | И | Л | И |
| И | Л | Л | И |
| И | И | И | Л |
Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
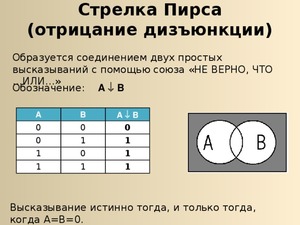
Стрелка Пирса
Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:
| А | Б | А или Б | не (А или Б) |
| Л | Л | Л | И |
| Л | И | И | Л |
| И | Л | И | И |
| И | И | И | Л |
| А | Б | не А | не Б | не А и не Б |
| Л | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | И |
| И | И | Л | Л | Л |
Определение эквивалентности
Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».
Здесь две переменных и пять действий. Строим таблицу:
| А | Б | В = (из А следует Б) | Г = (из Б следует А) | Д = А эквивалентно Б | Е = В и Г | Д эквивалентно Е |
| Л | Л | И | И | И | И | И |
| Л | И | И | Л | Л | Л | И |
| И | Л | Л | И | Л | Л | И |
| И | И | И | И | И | И | И |
В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
Таблицы истинности и логические схемы
Теория к заданию 2 из ЕГЭ по информатике
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
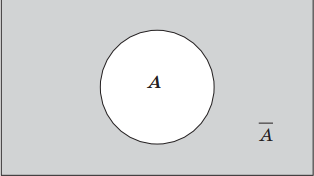
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖<->$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖<->$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
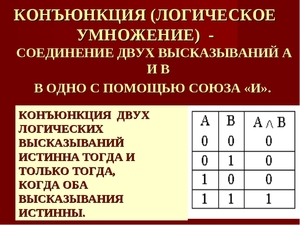
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
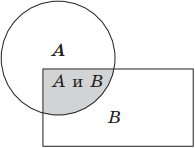
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если. то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ <->∧B) ∧ (A ∧ B↖<->)$ |
| Импликация | А → В | $A↖ <->∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ <->∧ B↖<->) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Таким образом, получена запись логической функции в КНФ.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $ |
| 0 | 0 | 0 |
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
Формула достаточно громоздка, и ее следует упростить:
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.