Как сравнить дроби
Как сравнить дроби
Сравнение обыкновенных дробей
Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Пример. Дробь 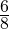

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь 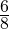

Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Пример. Дробь 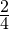

Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь 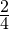

Сравнение дробей с разными знаменателями и числителями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Пример. Сравните дроби: 

Решение: приводим данные дроби к общему знаменателю:
Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как 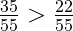

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.
Пример. Сравним дроби 
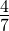
Решение: приводим данные дроби к общему знаменателю:
Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений
Так как 2 · 7 = 14, а 4 · 3 = 12, то
Значит, 
Теперь решим эту же задачу в общем виде, используя буквенную запись.
Пример. Пусть даны дроби 

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Пример. Сравните дробь 
Решение: представим число 5 в виде дроби со знаменателем 1:
Приводим дроби к общему знаменателю:
Сравниваем числители, так как 11 Пример.
Онлайн калькулятор сравнения дробей
Сравнение дробей
Содержание
 Сравнение дробей с одинаковыми знаменателями Сравнение дробей с одинаковыми знаменателями |
 Сравнение дробей с одинаковыми числителями Сравнение дробей с одинаковыми числителями |
 Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю |
 Приведение дробей к наименьшему общему знаменателю. Дополнительные множители Приведение дробей к наименьшему общему знаменателю. Дополнительные множители |
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Например, из двух дробей
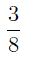
большей является дробь с числителем 5.
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Например, из двух дробей
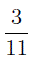
Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю
Для того, чтобы сравнить дроби с разными числителями и знаменателями, нужно сначала, пользуясь основным свойством дробей, привести их к соответственно равным дробям с одинаковыми знаменателями (привести к общему знаменателю), а затем сравнить полученные дроби, пользуясь методом сравнения дробей с одинаковыми знаменателями. Например, для того, чтобы сравнить дроби
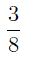
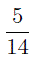
приведем их к дробям с общим знаменателем, равным произведению знаменателей этих дробей:
Приведение дробей к наименьшему общему знаменателю. Дополнительные множители
В разделе «Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю» мы сравнивали дроби при помощи их приведения к общему знаменателю, равному произведению знаменателей. Однако этот способ часто приводит к большим вычислениям. Иногда удается сократить вычисления, приводя дроби не просто к общему знаменателю, а к наименьшему общему знаменателю.
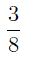
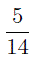
приведем их к дробям с наименьшим общим знаменателем, равным наименьшему общему кратному знаменателей этих дробей.
что и требовалось показать.
называют дополнительными множителями.
Сравнение дробей онлайн
Сравнить дроби это значит понять какая из них больше.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та у которой числитель больше
Сравним дроби 5/7 и 6/7
В первой дроби мы берём 5 частей из 7 а во второй 6 частей из 7. Соответственно 6 частей больше чем 5.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями нужно привести дроби к общему знаменателю а потом сравнить числители.
Сравним дроби 3/4 и 2/3
Для начала нужно найти наименьшее общее кратное знаменателей. НОК(4,3) = 12
Домножим первую дробь на 3, а вторую на 4.
Получится 9/12 > 8/12
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот
К примеру у нас есть яблоко. Пол яблока это 1/2. Треть яблока это 1/3. Лучше съесть пол яблока чем треть.
Сравнение смешанных дробей
Для сравнения смешанных дробей нужно преобразовать смешанную дробь в неправильную. Если знаменатели будут разными то привести дроби к общему знаменателю. Если одинаковыми то сравнить числители.
Сравнение дробей. Как сравнивать дроби с разными знаменателями?
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
Если мы до решаем эти дроби, то получим числа \(\frac<20> <4>= 5\) и \(\frac<20> <10>= 2\). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac<5> <10>\).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac<3> <5>\).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
Сравнение дробей: правила, примеры, решения
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
Рассмотрим данные действия на примере.
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Решение
Сравнение дроби с натуральным числом
Сравнение дробей: как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: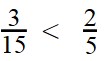
Сравнение дробей
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше ( )
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. 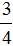

Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби 
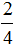

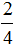

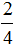
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. 
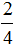
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби 

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби 
Умножим дроби на свои дополнительные множители:
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему 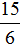

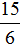

После выделения целой части в дроби 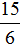
Теперь можно легко понять, почему 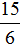

2 целые пиццы и 

Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10 − 8 = 2
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример 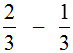
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. 
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения 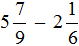
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби 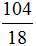
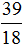
У дроби 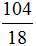
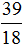
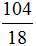
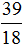
А это значит что уменьшаемое 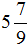
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Теперь сравним дроби 
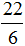

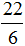

А это значит, что и уменьшаемое 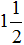
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
Теперь нужно сравнить дроби 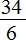

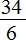

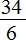

А это значит, что уменьшаемое 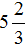
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ 
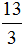

Сравнение дробей
Также как и натуральные числа обыкновенные дроби можно сравнивать.
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.
Равные дроби соответствует одной и той же точке на числовой оси.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2 ), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.
Любая неправильная дробь больше любой правильной.
Сравнение неправильных дробей правила и примеры.
Неправильные дроби сравниваем по тем же правилам, что и обыкновенные дроби или правильные дроби. Рассмотрим подробно эти правила.
Сравнение неправильных дробей с одинаковыми знаменателями.
Есть несколько правил сравнения неправильных дробей с одинаковыми знаменателями:
Рассмотрим пример:
Выполните сравнение неправильных дробей с одинаковыми знаменателями: а) \(\frac<20><13>\) и \(\frac<15><13>\) б) \(\frac<-161><57>\) и \(\frac<-98><57>\) г) \(\frac<17><3>\) и \(\frac<-11><3>\)
Решение:
а) Раз у дробей \(\frac<20><13>\) и \(\frac<15><13>\) одинаковые знаменатели переходим к сравнению числителей 20>15,
Сравнение неправильных дробей с одинаковыми числителями.
Пример:
Выполните сравнение неправильных дробей с одинаковыми числителями: а) \(\frac<21><9>\) и \(\frac<21><10>\) б) \(\frac<-15><3>\) и \(\frac<-15><4>\)
Решение:
а) У неправильных дробей с одинаковыми положительными числителями \(\frac<21><9>\) и \(\frac<21><10>\), та дробь больше, где знаменатель меньше 9 \frac<21><10>\)
б) У неправильных дробей с одинаковыми отрицательными числителями \(\frac<-15><3>\) и \(\frac<-15><4>\), та дробь больше где знаменатель больше 3 44, следовательно,
Сравнение неправильной дроби с правильной дробью.
Пример:
Сравните правильную дробь и неправильную дробь: а) \(\frac<14><13>\) и \(\frac<13><14>\) б) \(-\frac<27><6>\) и \(-\frac<17><18>\)
Решение:
а) Правильная и неправильная дробь положительны, поэтому неправильная дробь больше правильной дроби.
б) Правильная и неправильная дробь отрицательны, поэтому неправильная дробь меньше правильной дроби.
б) Неправильная дробь \(-\frac<4><3>\) отрицательна, поэтому \(0 1\)
Равные неправильные дроби.
Правило равных неправильных дробей:
Неправильные дроби равны тогда, когда при одинаковых знаменателях равны их числители. Например:
You may also like:
Сравнение рациональных чисел, определения и примеры.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов
— сравнение дробей с равными числителями;
— сравнение дробей с равными знаменателями;
— сравнение дробей с разными знаменателями.
Теоретический материал для самостоятельного изучения
На прошлых уроках мы научились приводить дробь к общему знаменателю и сокращать дробь.
Вспомним алгоритм приведения дробей к наименьшему общему знаменателю. Он предполагает следующие действия:
1. разложить на простые множители знаменатели дробей;
2. найти наименьшее общее кратное (НОК) для знаменателей данных дробей;
3. привести дроби к общему знаменателю, то есть умножить и числитель, и знаменатель дроби на множитель.
Также существует алгоритм сокращения дробей. Применяя его, например, для решения задачи, следует:
1. найти наибольший общий делитель (НОД) числителя и знаменателя;
2. разделить числитель и знаменатель на их НОД.
Используя полученные знания, мы научимся сегодня сравнивать обыкновенные дроби.
Чтобы сравнить дроби с разными знаменателями, необходимо привести дроби к общему знаменателю, а затем применить правило сравнения дробей с общим знаменателем.
Подведём итог. Чтобы сравнить две дроби, нужно выяснить, равны ли их знаменатели. Если да, то из двух дробей с общим знаменателем больше та дробь, у которой числитель больше. Если нет, то нужно привести дроби к общему знаменателю, а затем сравнить числители.
№ 1. Выберите пары дробей со знаком равно.
Чтобы сравнить вторую пару дробей, сократим их:
Сравнение дробей
Время чтения: 10 минут
Когда дело доходит до дробей, мы обычно сравниваем две или более. На самом деле, мы сталкиваемся с дробями в нашей повседневной жизни. Простой пример: если вы разрезаете яблоко на две части, оно тоже будет дробью. В принципе, сравнение двух дробей означает определение большей и меньшей части среди них.
Понятие сравнения дробей
Такие числа, как \[\frac<1><2>, \frac<2><3>, \frac<3><4>, \frac<1><17>\] известны как дроби.
Число под линией деления называется знаменателем. Оно описывает нам, на сколько равных частей делится целое. Число над строкой называется числителем. Оно говорит нам, сколько равных частей взято.
Пример: \[\frac<3><7>, \frac<5><19>, \frac<3><116>\] и т.д. являются дробями.
Сравнить две дроби – это значит понять, какая из них больше, а какая меньше. Из двух дробей с равными знаменателями больше будет та, у которой числитель больше, и меньше та, у которой числитель меньше. Примеры сравнения дробей в реальном времени включают различные действия, такие как проверка сниженных цен во время покупок, достижение продаж определенного продукта, медицинские рецепты врача, результаты тестов и экзаменов и т.д. Опять же, сравнение дробей – это то, что мы испытываем или с чем сталкиваемся в своей повседневной жизни. Если достаточно сосредоточиться, то можно легко получить практическое представление об одном и том же каждый день, выполняя обычные домашние дела и математические вычисления.
Правила сравнения дробей
Есть несколько правил, которым мы должны следовать при сравнении дробей:
Сравнение дробей с одинаковыми знаменателями
Подобные дроби — это две или более фракции, имеющие один и тот же знаменатель.
Пример: \[\frac<3><7>, \frac<5><7>, \frac<6><7>\] являются «подобными дробям».
Сравнение подобных дробей
В этом методе необходимо проверить, совпадают ли знаменатели или нет. Если знаменатели одинаковы, то дробь с большим числителем является более значительной дробью. Дробь с меньшим числителем – это меньшая дробь. Если и числители, и знаменатели равны, то дроби также идентичны. Пример: Давайте сравним \[\frac<6><17>\] и \[\frac<16><17>\].
Сравнение дробей с разными знаменателями
Неподобные дроби — это две или более дроби имеющие разные знаменатели.
Пример: \[\frac<5><17>\] и \[\frac<3><14>\] являются неподобными дробями.
Сравнение неподобных дробей
Чтобы сравнить дроби с разными знаменателями, следует начать с поиска наименьшего общего знаменателя, чтобы сделать их значения одинаковыми. Когда знаменатели преобразуются в одни и те же знаменатели, то дробь с большим числителем является более значимой — например, \[\frac<1><2>\] и \[\frac<2><5>\].
Если знаменатели разные, а числители одинаковые, то можно легко сравнить дроби, посмотрев на их знаменатели. Дробь с меньшим знаменателем имеет большее значение. Дробь с большим знаменателем имеет меньшее значение.
Десятичный метод сравнения дробей
В этом методе необходимо сравнить десятичные значения дробей. Сначала числитель делится на знаменатель, а затем дробь преобразуется в десятичную дробь. Затем сравниваются десятичные значения.
Сравнение дробей с помощью перекрестного умножения
В этом методе числитель одной дроби перекрестно умножается на знаменатель другой дроби.
Пример: \[\frac<1> <2>\text < и >\frac<3><4>\], когда мы перекрестно умножаем, мы получаем 1×4=4 и 2×3=6.
Решение примеров на сравнение дробей
1. Сравните две дроби \[\frac<4><7>\] и \[\frac<2><7>\].
Ответ: Мы видим, что знаменатели в данных дробях одинаковы. Здесь мы будем следовать правилу, согласно которому, когда знаменатели дроби одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем считается большей дробью.
Итак, сравните числители 4>2
2. Сравните две заданные дроби: \[\frac<6><13>\] и \[\frac<6><20>\].
Ответ: Мы видим, что числители в данных дробях одинаковы. Здесь мы будем следовать правилу, что, когда дроби имеют одинаковый числитель, чем меньше знаменатель, тем больше дробь.
Итак, сравните знаменатели 13>20
3. Сравните данные дроби, используя метод перекрестного умножения: \[\frac<3><8>\] и \[\frac<5><10>\].
Ответ: Мы будем использовать метод перекрестного умножения, поэтому это означает, что необходимо умножить 3×10=30 и 5×8=40.
Как правильно сравнивать дроби с разными знаменателями
Что такое дробь
Дробь является числом, в состав которого входит одна, либо несколько равных частей (долей) единицы.
Исходя из метода записи, дроби подразделяют на следующие виды:
Здесь над чертой расположен числитель, а под чертой находится знаменатель. Числитель является делимым, а знаменатель обозначает делитель.
В процессе сравнения пары обыкновенных дробей необходимо определить их общий знаменатель. После того как дроби приведены к единому знаменателю, их достаточно просто сравнить. Если числитель одной дроби больше по сравнению с числителем другой дроби, то первая дробь соответственно будет больше, чем вторая.
Попробуем выполнить самостоятельную работу по сравнению дробей. Предположим, что имеется пара дробей, которые нужно сравнить:
Найдем общий знаменатель:
Далее по алгоритму можно привести дроби к данному знаменателю 20:
3 4 = 15 20 ; 4 5 = 16 20
Сравнение обыкновенных дробных выражений
Нередко при решении различных задач в средних классах требуется сравнить неодинаковые дроби и описать ход решения. Наиболее простым случаем является условие, при котором дроби, в том числе смешанные, обладают одинаковыми знаменателями и разными числителями. Тогда следует руководствоваться правилом.
Если две дроби имеют идентичные знаменатели, то больше из них та, которая обладает большим числителем по сравнению со второй дробью. С другой стороны, меньше будет та дробь, которая имеет меньший числитель.
Рассмотрим, как пример, две дроби, которые необходимо сравнить:
Наглядно рассмотреть задачу можно на примере пиццы. Представим, что она разделена на 4 части. Из рисунка видно, что 3 4 пиццы больше по сравнению с 2 4 пиццы.
Сравнение дробей с разными знаменателями
Более сложным вариантом заданий являются такие, которые предполагают сравнение дробей с одинаковыми числителями и разными знаменателями. При этом целесообразно обратиться к правилу.
Когда дроби имеют одинаковые числители, то большей считается та дробь, которая обладает меньшим знаменателем. С другой стороны, из дробей с идентичными числителями будет меньше та, которая имеет больший знаменатель.
В качестве примера рассмотрим две дроби, которые нужно сравнить:
Возникает вопрос, как сравнить дроби, которые обладают не только разными знаменателями, но и отличаются своими числителями. Разобрать метод сравнения в этом случае следует на примере двух дробей, которые не являются отрицательными:
В первую очередь определим общий знаменатель для этих дробей. Заметим, что наименьшим общим кратным знаменателей и в том и в другом случае является число 6. Зная НОК, определим дополнительные множители для каждой из дробей путем деления наименьшего общего кратного на знаменатель:
Затем следует выполнить умножение дробей и их дополнительных множителей:
В результате получились дроби, имеющие одинаковые знаменатели. Вспомним, что, если две дроби имеют идентичные знаменатели, то больше из них та, которая обладает большим числителем по сравнению со второй дробью.
Применимо к нашей задаче:
Визуально сравнить эти дроби можно с помощью изображения пиццы:
Пояснение на примерах
Даны две дроби, которые требуется сравнить:
Заметим, что данные дроби обладают идентичными знаменателями. Они равны 26. В таком случае остается лишь сравнить числители. Получим:
Ответ: 7 26 13 26
На столе стоит торт. К столу присоединятся 5 или 11 гостей. В том случае, если придут 5 гостей, то торт необходимо будет поделить на 5 одинаковых частей. Для 11 гостей требуется разрезать торт на 11 равных кусков. Нужно определить, в каком случае гости получат по куску большего размера.
Вспомним правило: когда дроби имеют одинаковые числители, то большей считается та дробь, которая обладает меньшим знаменателем. С другой стороны, из дробей с идентичными числителями будет меньше та, которая имеет больший знаменатель.
Ответ: когда придут 5 гостей, каждый из них получит кусок торта большего размера по сравнению с частями торта, поделенного на 11 человек.
У девочки есть 20 карамелек. Она может угостить 4 или 10 друзей, разделив между ними конфеты поровну. Нужно определить, в каком случае каждый из друзей получит большее количество карамелек.
Ответ: если поделить конфеты между 4 друзьями, то каждому из них достанется карамелек больше, чем в том случае, когда эти конфеты раздали 11 друзьям.
Имеются дроби, которые нужно сравнить:
Заметим, что эти дроби имеют одинаковые числители. Поэтому дробь с меньшим знаменателем больше:
Ответ: 1 17 1 15
Требуется сравнить две дроби:
Приведем записанные дроби к общему знаменателю. Единым знаменателем в данном случае является число 21. Выполним преобразования:
2 3 = 2 × 7 3 × 7 = 14 21
5 7 = 5 × 3 7 × 3 = 15 21
Далее необходимо сравнить между собой числители, исходя из правила сравнения дробей с идентичными знаменателями:
Имеются две дроби, которые нужно сравнить:
Заметим, что дробь 8 7 является неправильной и больше, чем единица:
С другой стороны, дробь 11 13 является правильной и меньше, чем единица:
Ответ: 11 13 8 7
Нужно сравнить две дроби:
Отсутствие идентичных числителей и знаменателей говорит о необходимости использовать в решении задания правило, по которому сравнивают дроби с разными знаменателями.
В первую очередь требуется вычислить общий знаменатель. Он равен 96. Далее следует привести дроби к этому знаменателю. Для этого первую из дробей нужно умножить на 8, а вторую — умножить на 6.
11 12 = 11 × 8 12 × 8 = 88 96
13 16 = 13 × 6 16 × 6 = 78 96
Сравним числители полученных в результате преобразования дробей. Если у дроби числитель больше, то и сама она больше по сравнению с той, числитель которой меньше.
Ответ: 11 12 > 13 16
Папа и сын играли в футбол. Мальчик сделал 10 подходов, из которых забил 5 раз гол. Отец сделал 5 подходов, из которых 3 были успешными. Нужно оценить, у кого результат игры был лучше.
Запишем условия задачи в виде дробей:
Выполним сравнение этих дробей путем приведения их к единому знаменателю, который равен в данном случае 10.
3 5 = 3 × 2 5 × 2 = 6 10
Ответ: папа показал лучший результат игры в футбол.
Сравнение дробей
Равные дроби
Две дроби называются равными, если равны их числители и знаменатели соответственно.
Две дроби считаются равным, если величины, выражаемые этими числами при одной и той же единице измерения, равны между собой.
Принципы сравнения дробей
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Любая правильная дробь меньше произвольной неправильной дроби.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю. Для этого приводят либо к общему знаменателю, либо числитель и знаменатель первой дроби домножают на знаменатель второй и наоборот, числитель и знаменатель второй дроби на знаменатель первой. И далее дроби сравнивать как дроби с одинаковым знаменателем (описано выше).
Дроби. Сравнение дробей.
Правила сравнения обыкновенных дробей зависят от вида дроби (правильная, неправильная, смешанная дробь) и от знаменателей (одинаковые или разные) у сравниваемых дробей. Правило. Чтобы сравнить две дроби с одинаковыми знаменателями, надо сравнить их числители. Больше (меньше) та дробь, у которой числитель больше (меньше). Например, сравнить дроби:
Сравнение правильных, неправильных и смешанных дробей между собой.
Правило. Неправильная и смешанная дроби всегда больше любой правильной дроби. Правильная дробь по определению меньше 1, поэтому неправильная и смешанная дроби (имеющие в своем составе число, равное или больше 1) больше правильной дроби.
Правило. Из двух смешанных дробей больше (меньше) та, у которой целая часть дроби больше (меньше). При равенстве целых частей смешанных дробей больше (меньше) та дробь, у которой больше (меньше) дробная часть.
Например, сравнить дроби:
Аналогично сравнению натуральных чисел на числовой оси большая дробь стоит правее меньшей дроби.
Как сравнить дроби
На данной странице калькулятор онлайн для сравнения дробей. Этот калькулятор сравнивает обычные дроби и десятичные. При сравнении выводится описание.
Сравнить дроби
Как сравнить дроби с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Как сравнить дроби с одинаковыми числителями
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
Как сравнить дроби с разными знаменателями
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Когда дроби будут приведены к общему знаменателю, то их сравнивают по правилу, когда знаменатели равны.
Неправильная дробь всегда больше правильной дроби.
Неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Сравнение дробей: правила, примеры, решения.
В центре внимания данной статьи стоит сравнение дробей. Мы уже знаем про равные и неравные дроби. Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.
Навигация по странице.
Сравнение дробей с одинаковыми знаменателями
Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.
Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.
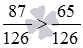
Сравнение дробей с разными знаменателями
Сравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю.
Разберем решение примера.
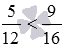
Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом.
Рассмотрим сравнение дробей с разными знаменателями этим способом.
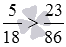
Сравнение дробей с одинаковыми числителями
Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.
Существует такое правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.
Рассмотрим решение примера.
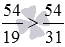
В заключение этого пункта приведем пример, хорошо иллюстрирующий основную суть озвученного правила сравнения дробей с одинаковыми числителями. Пусть перед нами две тарелки, на одной из них 1/2 пирога, а на другой 1/16 этого же пирога. Понятно, что скушав половину пирога, мы будем куда больше сыты, чем съев 1/16 его часть.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом сводится к сравнению двух дробей, если число записать в виде дроби со знаменателем 1 (смотрите натуральное число как дробь со знаменателем 1). Рассмотрим решение примера.
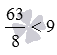
Сравнение дробей
2 сентября 2011
В этом уроке мы научимся сравнивать дроби между собой. Это очень полезный навык, который необходим для решения целого класса более сложных задач.
Для начала напомню определение равенства дробей:
Во всех остальных случаях дроби являются неравными, и для них справедливо одно из следующих утверждений:
Конечно, в приведенных примерах с нулями был явный перебор, но смысл именно такой: заполнить недостающие разряды слева, а затем сравнить.
По определению имеем:
К сожалению, приведенная схема сравнения десятичных дробей не универсальна. Этим методом можно сравнивать только положительные числа. В общем же случае алгоритм работы следующий:
Ну как, неслабо? Сейчас рассмотрим конкретные примеры — и все станет понятно.
Урок 11 Бесплатно Сравнение дробей с разными знаменателями
На этом уроке мы научимся сравнивать дроби с одинаковыми знаменателями, с одинаковыми числителями, с разными числителями и знаменателями. А также закрепим навыки, решив несколько примеров и упражнений.
Сравнение дробей с одинаковыми числителями
Дробная черта заменяет знак деления.
Представьте, что торт разделили в первом случае на пять частей, а во втором случае на семь.
Понятно, что если пришло пятеро гостей, то в первом случае каждому гостю достанется больший кусок торта, чем во втором случае.
Если дроби имеют одинаковые числители, то больше та дробь, у которой меньше знаменатель.
Пример 1
Решение:
Любая правильная дробь всегда меньше 1.
Если дробь неправильная, то она больше единицы.
Например, \(\mathbf<\frac<2> <3>1>\), потому что дробь \(\mathbf<\frac<5><3>>\)- неправильная.
Error: /home/l/ladle/public_html/system/cache/templates_c/8d07a1dd7ab308e05d7a9da903f0510e.php does not exists!
Сравнение дробей с разными числителями и знаменателями
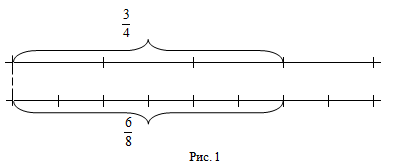
По иллюстрации видно, что \(\mathbf<\frac<1><8>>\) меньше половины, а \(\mathbf<\frac<4><7>>\)- больше половины. Следовательно, \(\mathbf<\frac<1><8>>\) \(\mathbf<\frac<2><4>>\), следовательно, и \(\mathbf<\frac<3><4>>\) > \(\mathbf<\frac<1><2>>\)
Пример 1
Решение:
Сравнение дробей с помощью числового луча
Разделим пиццу на 8 равных частей. 4 части вместе составляют половину пиццы.
Значит, \(\mathbf<\frac<4><8>>\) пиццы равны \(\mathbf<\frac<1><2>>\)пиццы. Поэтому говорят, что дроби \(\mathbf<\frac<4><8>>\) и \(\mathbf<\frac<1><2>>\) равны, и пишут: \(\mathbf<\frac<4> <8>= \frac<1><2>>\)
На координатном луче равные дроби соответствуют одной и той же точке.
Две равные дроби обозначают одно и то же дробное число.
Сравним две разные дроби с помощью числового луча.
Точка M(\(\mathbf<\frac<5><7>>\)) лежит справа от точки K(\(\mathbf<\frac<2><7>>\))
Точка на координатном луче, имеющая большую координату, лежит справа от точки, имеющей меньшую координату.
Мы рассмотрели все возможные способы сравнения обыкновенных дробей, познакомились с универсальным способом сравнения дробей с разными знаменателями: приведением дробей к общему знаменателю.
В качестве дополнительного множителя всегда подойдет знаменатель другой дроби.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня мы с вами занимались сравнением дробей. Например, мы сравнивали дроби с одинаковыми числителями. Особое место среди них занимают египетские дроби. Их свойство заключается в том, что они записываются в виде суммы нескольких дробей, у которых в числителе стоит 1.
Из названия понятно, что изобрели их в Египте в глубокой древности. Из старых свитков и математических папирусов современники узнали, что египтяне пользовались своей таблицей дробей для чисел вида \(\mathbf<\frac<2>
Кроме самой таблицы были обнаружены 64 задачи, решённые с помощью них.
Для обозначения единицы египтяне использовали значок, похожий на глаз. Он назывался ер (один из) или рот. Довольно интересную запись привычных нам дробей можно увидеть на рисунке ниже.
Разложенные таким образом дроби не всегда удобно будет сравнивать. В сумме может быть много слагаемых и можно легко запутаться, поэтому проще пользоваться посчитанными суммами.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Урок 34 Бесплатно Сравнение дробей
Ранее нами были изучены обыкновенные дроби, а также основное свойство дроби.
Также, вам, наверное, известно, что натуральные числа можно сравнивать, и вы возможно уже задавались таким вопросом.
Если обыкновенные дроби, как и натуральные числа, представляют собой оценку количества чего-либо, можно ли их сравнивать?
За время этого урока мы узнаем, как сравнивать обыкновенные дроби.
Познакомится со способам сравнения дробей с одинаковым знаменателем.
Познакомимся со способом сравнения дробей с одинаковым числителем.
А также мы рассмотрим универсальные способы сравнения обыкновенных дробей.
Сравнение дробей с одинаковым знаменателем
Рассмотрим, как можно сравнивать дроби с одинаковым знаменателем на примере.
Давайте сравним следующие дроби с одинаковым знаменателем \(\mathbf<\frac<3><7>>\), \(\mathbf<\frac<5><7>>\), \(\mathbf<\frac<1><7>>\), разделив отрезок на 7 равных частей.
Теперь, если мы будем сравнивать наши дроби как длины частей отрезка, то мы увидим, что:
Подобные рассуждения верны не только в случае деления отрезка на равные части и сравнения длин.
Если представить, что у нас есть торт, и мы разделили его на несколько равных частей, то чем больше частей торта мы возьмем, тем больше торта нам достанется.
Для любых других примеров подобные рассуждения будут приводить к одному и тому же результату.
Сформулируем его в виде правила.
Из двух дробей с одинаковым знаменателем меньше та дробь, у которой числитель меньше.
И наоборот, из двух дробей с одинаковым знаменателем больше та дробь, у которой числитель больше.
В случае если у дробей с одинаковым знаменателем числители равны, то и дроби считаются равными.
Сравнение дробей с одинаковым числителем
Не составляет труда и сравнение дробей с одинаковым числителем.
Представьте, что вы на свой день рождения приготовили 3 пиццы и поровну делите их между своими гостями.
Чем больше гостей на вашем празднике, тем меньше кусков пиццы им достанется.
Так если к вам пришло 6 гостей, то каждый получит по \(\mathbf<\frac<3><6>>\) от всех пицц, а если пришло 7 гостей, то каждый получит по \(\mathbf<\frac<3><7>>\) от всех пицц.
Аналогичные рассуждения верны и для других дробей с одинаковым числителем.
Давайте разрежем один и тот же круг на разное число одинаковых частей и раскрасим в каждом случае ровно 2 части.
Видно, что чем больше разрезов мы сделали, тем меньше получаются кусочки, а значит, и два кусочка вместе будут составлять меньшею часть круга.
Из таких наблюдений можно сделать вывод, что:
Из двух дробей с одинаковым числителем меньше та дробь, у которой знаменатель больше.
И наоборот, из двух дробей с одинаковым числителем больше та дробь, у которой знаменатель меньше.
В случае если у дробей с одинаковым числителем знаменатели равны, то и дроби считаются равными.
Пройти тест и получить оценку можно после входа или регистрации
Универсальный способ сравнения дробей. Приведение к общему знаменателю
Возникает вопрос, как сравнивать дроби, у которых разные и числители, и знаменатели.
Предположим нам надо сравнить \(\mathbf<\frac<3><4>>\) и \(\mathbf<\frac<2><3>>\)
Давайте разделим круг на 12 равных частей.
Заметим, что теперь четверть круга состоит из 3 частей, а значит, взять \(\mathbf<\frac<3><4>>\) круга это все равно что взять \(\mathbf<\frac<9><12>>\) круга.
Также, заметим, что теперь треть круга состоит из 4 частей, а значит, взять \(\mathbf<\frac<2><3>>\) все равно что взять \(\mathbf<\frac<8><12>>\) круга.
Описанный выше пример является иллюстрацией к правилу сравнения дробей приведением к общему знаменателю.
Метод заключается в том, что нам нужно, воспользовавшись основным свойством дроби, домножить числитель и знаменатель каждой из двух дробей таким образом, чтобы их знаменатели совпали.
После этого мы сможем сравнить дроби, воспользовавшись уже известным нам правилом сравнения дробей с одинаковым знаменателем.
Еще один пример:
Пройти тест и получить оценку можно после входа или регистрации
Универсальный способ сравнения дробей. Приведение к наименьшему общему знаменателю
До этого мы рассмотрели наивный способ приведения дробей к общему знаменателю.
В нем мы в качестве общего знаменателя выбирали произведение знаменателей двух дробей.
Этот способ рабочий, но иногда приводит к громоздким вычислениям.
Так, например, если нам надо сравнить дроби \(\mathbf<\frac<3><24>>\) и \(\mathbf<\frac<7><48>>\), мы можем в качестве общего знаменателя выбрать \(\mathbf<24\cdot48>\), а можем просто домножить числитель и знаменатель первой дроби на 2, приведя таким образом дроби к общему знаменателю 48.
Рассмотрим снова сравнение дробей \(\mathbf<\frac<3><8>>\) и \(\mathbf<\frac<5><6>>\).
Ранее для сравнения этих дробей, мы приводили их к общему знаменателю \(\mathbf<6\cdot8=48>\), однако, гораздо проще привести их к наименьшему общему знаменателю 24.
Такой способ сравнения дробей называется приведение к наименьшему общему знаменателю.
У меня есть дополнительная информация к этой части урока!
Наименьший общий знаменатель двух дробей равен наименьшему общему кратному знаменателей этих дробей.
Для нахождения наименьшего общего кратного нужно разложить каждое из двух чисел в произведение простых множителей.
Затем нужно выделить общую часть в разложении на простые множители.
Тогда наименьшим общим кратным двух чисел будет частное произведения исходных чисел и общей части в разложении на простые множители.
Рассмотрим на примере:
Найдем наименьшее общее кратное чисел 12 и 8.
Разложим каждое из них в произведение простых множителей.
Общая часть в разложении:
Тогда наименьшее общее кратное:
Таким действием мы по сути избавляемся от дублирования общей части.
В итоге мы получаем число, являющееся произведением общей части на каждую из двух уникальных частей в разложении на простые множители, а значит, найденное таким образом число действительно будет делится на каждое из двух исходных чисел.
Пройти тест и получить оценку можно после входа или регистрации
5.4.6. Сравнение обыкновенных дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше. На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.
Получается, что делили каждый целый круг на одно и то же число 5, а брали разное количество частей: больше взяли — большая дробь и получилась.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?
Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.
Примеры. Сравнить обыкновенные дроби:
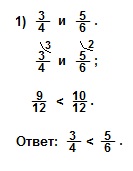
Правила сравнения обыкновенных дробей
В данной публикации мы рассмотрим, какие дроби являются равными, а также как сравнить две дроби с одинаковыми числителями/знаменателями или с разными знаменателями.
Равные дроби
Две дроби являются равными, если их числители и знаменатели соответственно равны (пропорционально равны).
равны, т.к. числитель и знаменатель первой дроби в два раза меньше числителя и знаменателя второй дроби.
Равные дроби соответствует:
Сравнение простых дробей
С одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, больше та, у которой числитель больше.
С одинаковыми числителями
Из двух дробей с одинаковыми числителями, больше та, у которой знаменатель меньше.
, т.к. 4 С разными знаменателями
Для того, чтобы иметь возможность сравнить дроби с разными знаменателями, для начала их нужно привести к общему знаменателю, после чего их уже можно сравнить по одинаковому знаменателю.
В данном случае нам нужно представить первую дробь со знаменателем 16 путем умножения числителя и знаменателя на число 2.
Теперь у нас имеются две дроби с одинаковыми знаменателями, которые мы можем сравнить по соответствующему правилу, рассмотренному выше.
Сравнение дробей онлайн
Сравнить дроби это значит понять какая из них больше.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та у которой числитель больше
Сравним дроби 5/7 и 6/7
В первой дроби мы берём 5 частей из 7 а во второй 6 частей из 7. Соответственно 6 частей больше чем 5.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями нужно привести дроби к общему знаменателю а потом сравнить числители.
Сравним дроби 3/4 и 2/3
Для начала нужно найти наименьшее общее кратное знаменателей. НОК(4,3) = 12
Домножим первую дробь на 3, а вторую на 4.
Получится 9/12 > 8/12
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот
К примеру у нас есть яблоко. Пол яблока это 1/2. Треть яблока это 1/3. Лучше съесть пол яблока чем треть.
Сравнение смешанных дробей
Для сравнения смешанных дробей нужно преобразовать смешанную дробь в неправильную. Если знаменатели будут разными то привести дроби к общему знаменателю. Если одинаковыми то сравнить числители.
Сравнение десятичных дробей
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Сотые с сотыми: 0
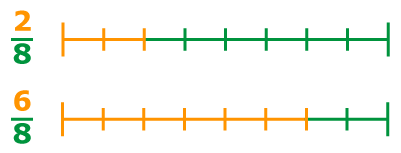



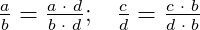

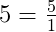



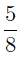
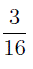
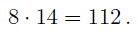
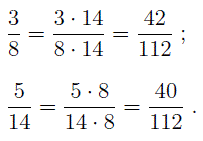
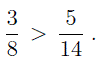
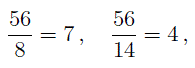
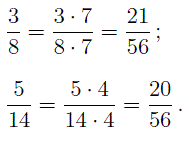


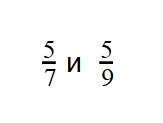
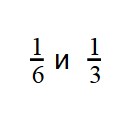
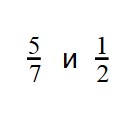
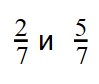
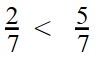
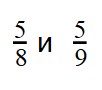
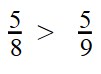
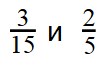

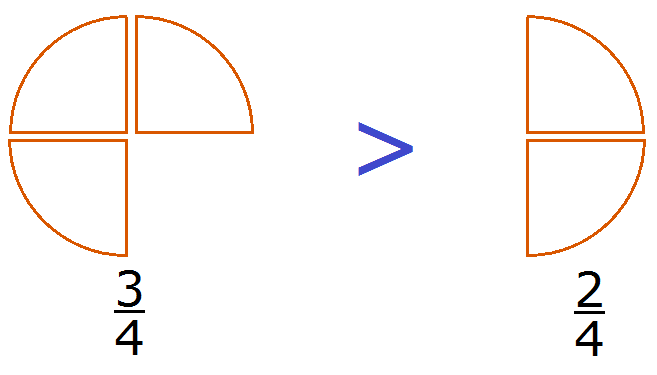
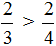

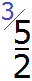

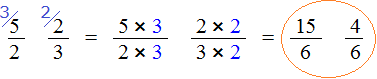
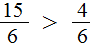
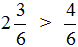
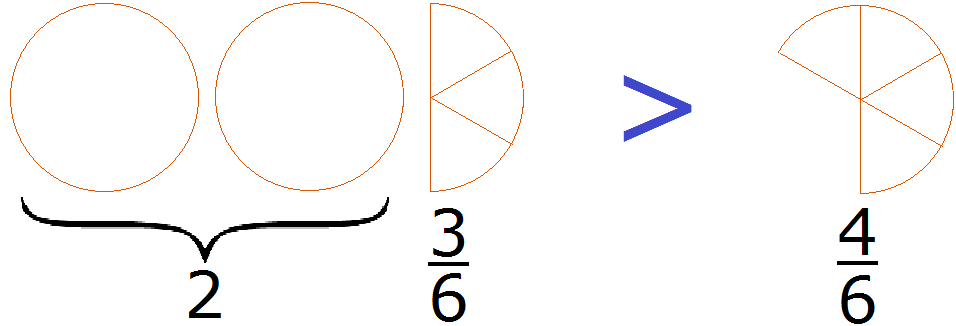

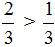
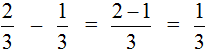
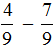
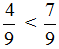
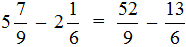
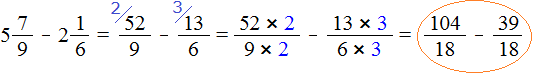
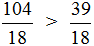

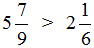
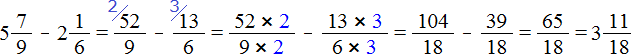
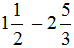
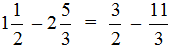
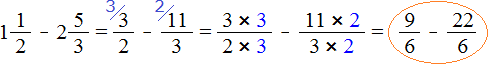
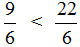
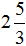
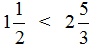


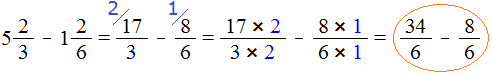
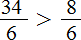
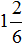
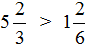
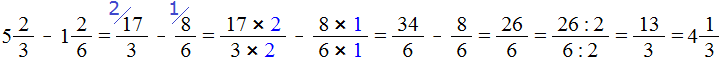











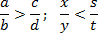
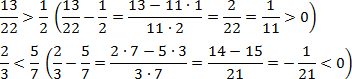











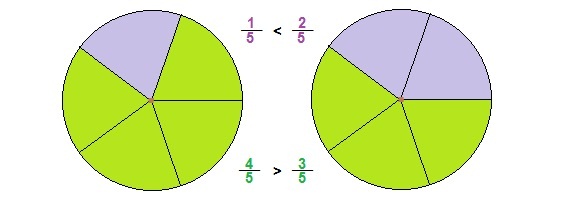
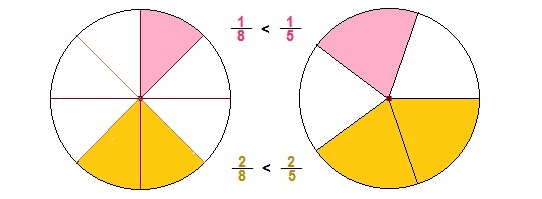
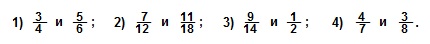

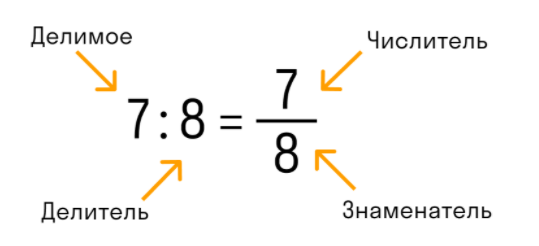

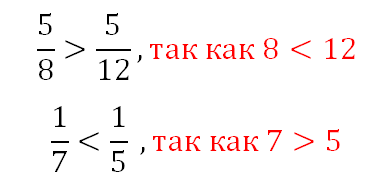




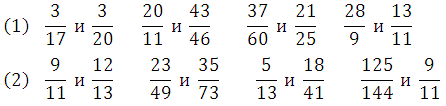







 Видно, что первая дробь меньше 0,5. Почему? Если выразить подробно, то:
Видно, что первая дробь меньше 0,5. Почему? Если выразить подробно, то: а вторая больше 0,5:
а вторая больше 0,5:







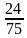 и
и 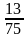 ; 3)
; 3)  и
и 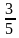 ; 5)
; 5) 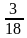 и
и 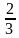 ;
;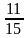 и
и  4)
4) 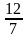 и
и 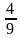 ; 6)
; 6) 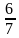 и
и  ;
;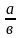
 , если а с
, если а с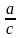 , если в
, если в ;
; 
 и ; и ; и
и ; и ; и