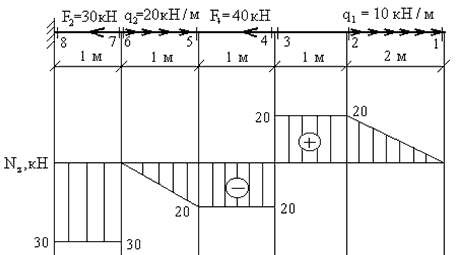
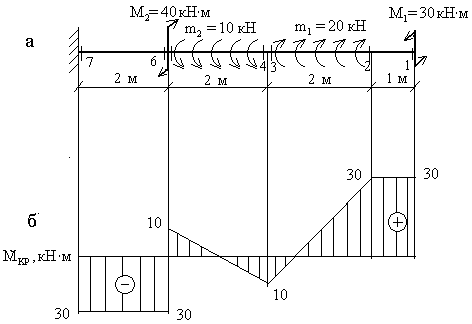
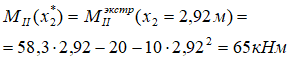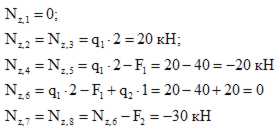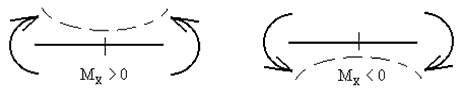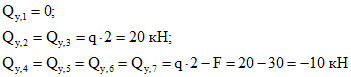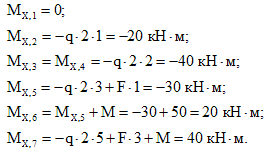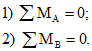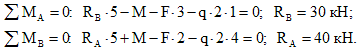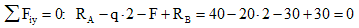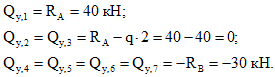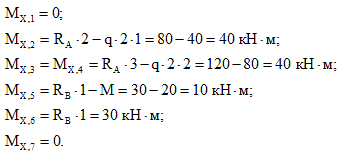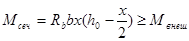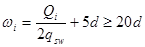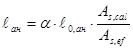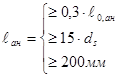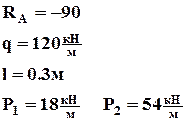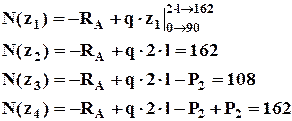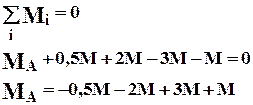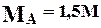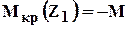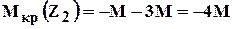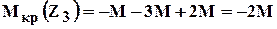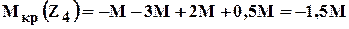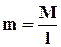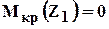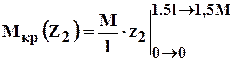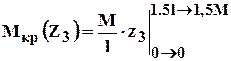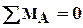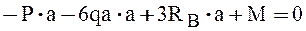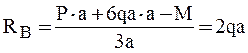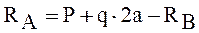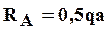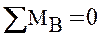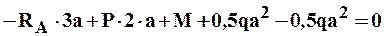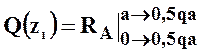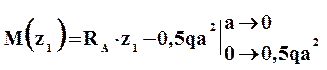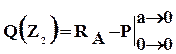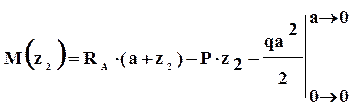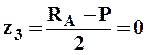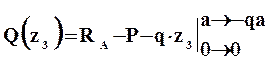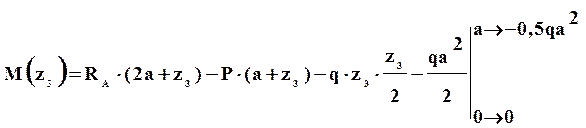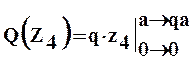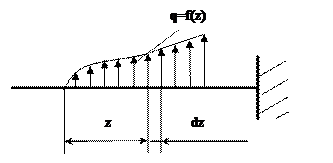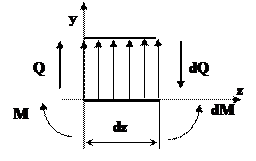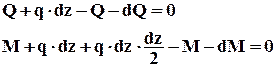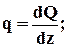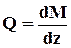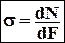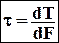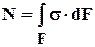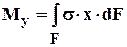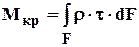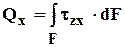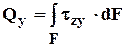Как строить эпюры

iSopromat.ru

Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

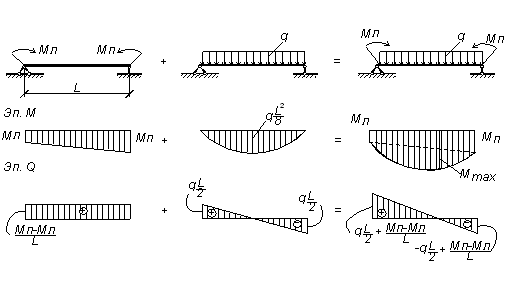
Эпюры при чистом изгибе

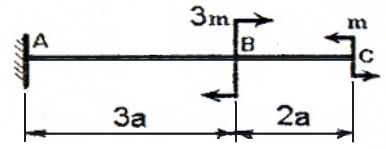
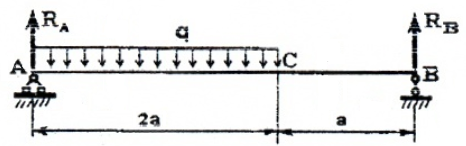
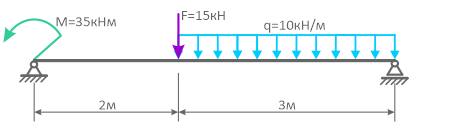
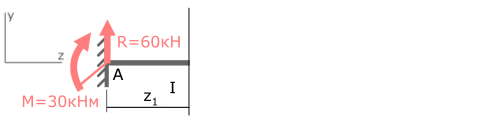
Для консольной балки:

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z₁ ≥ 2a (рис. 2 а,г)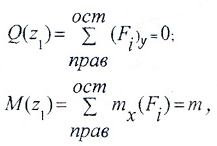

т.е. Q(z₁)=0 на всем участке, а M(z₁)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z₂ ≥ 5a (рис. 2 а,д)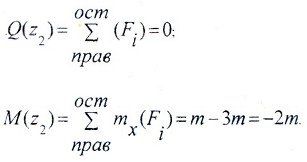

Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: M_max=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

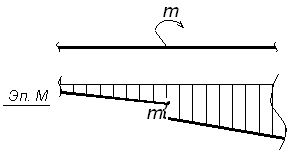
Эпюры при поперечном изгибе

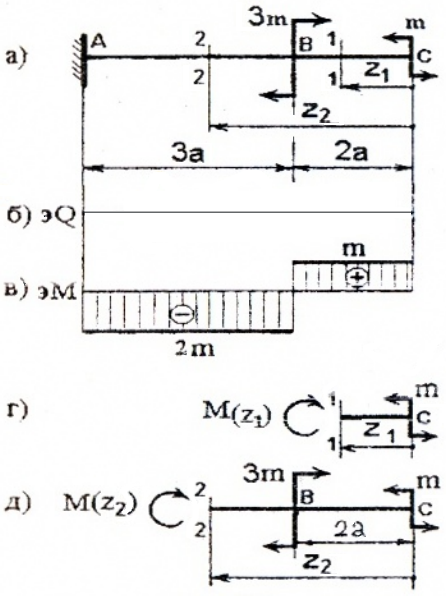
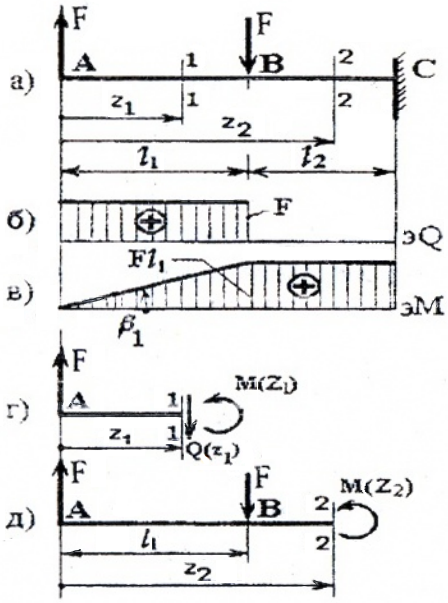
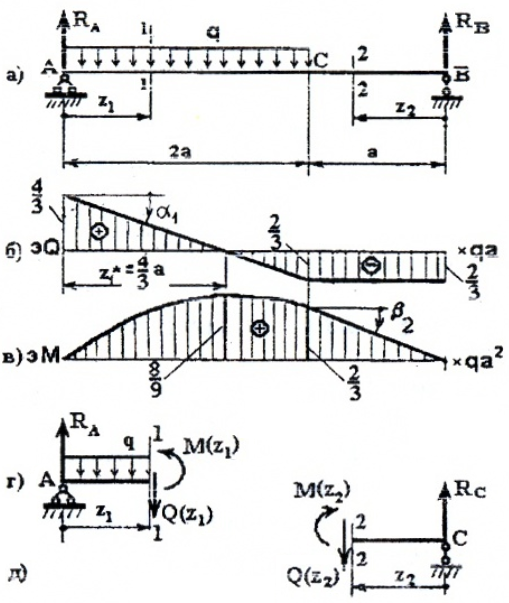
Построение эпюр Q и M для балки, изображенной на рис. 3

проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.

I силовой участок (AB): 0 ≥ z₁ ≥ l₁ (рис. 4, а, г)
Q(z₁)= F=const, на всем участке постоянная величина,
M(z₁)=F×z₁, уравнение прямой, график строим по двум граничным точкам:
M(z₁=0)=F×0=0 – в сечении A;
M(z₁=l₁)=F× l₁ — в сечении B.

Опасным является сечение B, в котором действуют Q_max=F, M_max=Fl₁.

Геометрическая проверка эпюр

Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим: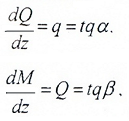

где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α₁=0 (линия эпюры Q горизонтальна), следовательно,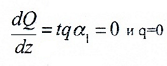

распределенная нагрузка отсутствует;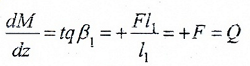

функция M (z₁) – возрастающая.

На участке “BC”: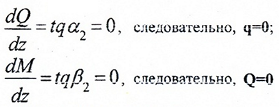

Так как все дифференциальные проверки выполняются, эпюры построены верно.

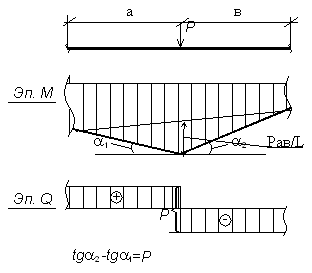
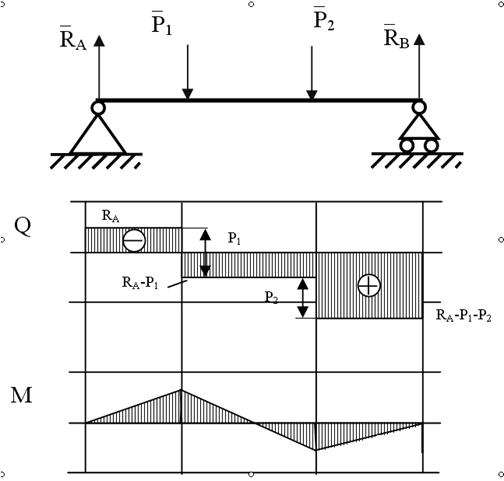
Эпюры для двухопорных балок

Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),

необходимо вначале найти опорные реакции и только потом строить эпюры.

Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑M_A=0 и ∑M_B=0.

Записываем уравнения и находим значения реакций: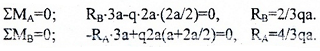

Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑F_Y=0 или ∑M_С=0.

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).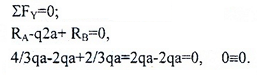

Для построения эпюр рассмотрим два силовых участка:

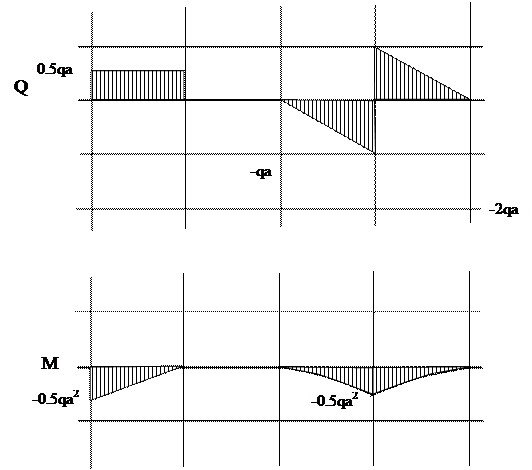
I участок (AC): 0 ≥ z₁ ≥2a (рис. 6, а, г)
Q(z₁)=R_A-qz₁ — прямая, которую строим по двум граничным точкам: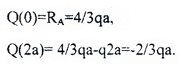

M(z₁)=R_Az₁-qz₁(z₁/2)= R_Az₁-qz₁ 2 /2 – парабола.

II силовой участок: 0 ≥ z₂ ≥ a.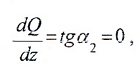

следовательно, q=0.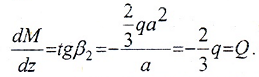

функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z₁*=4/3a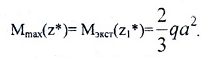

По силе в сечении «A»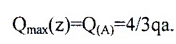

После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

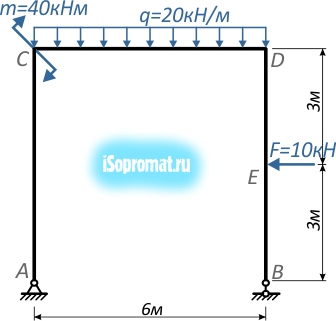
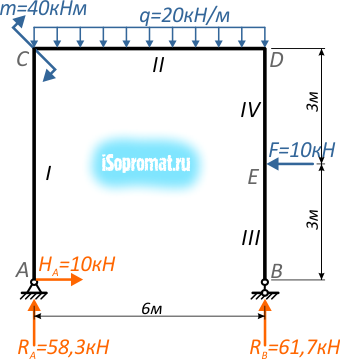
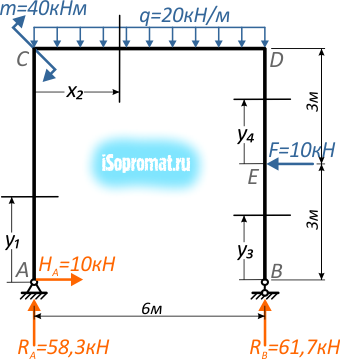
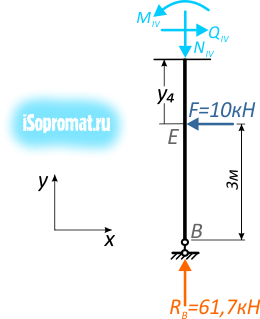
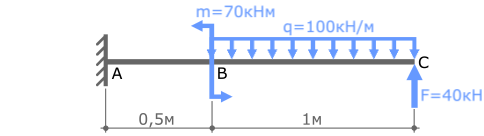
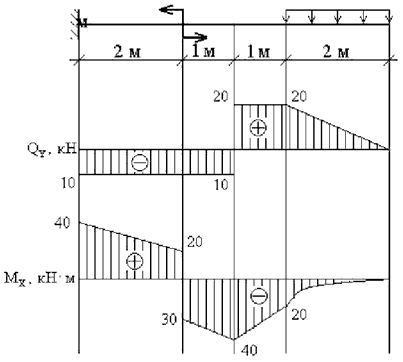
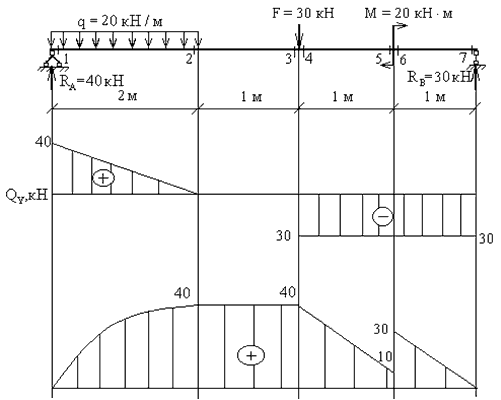
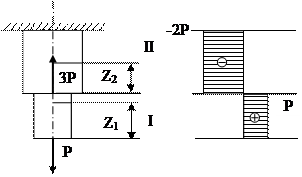
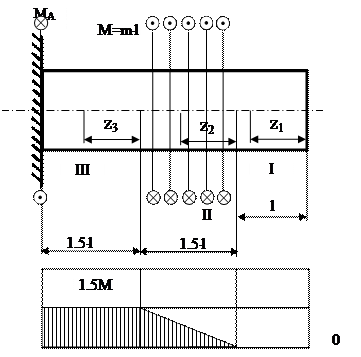
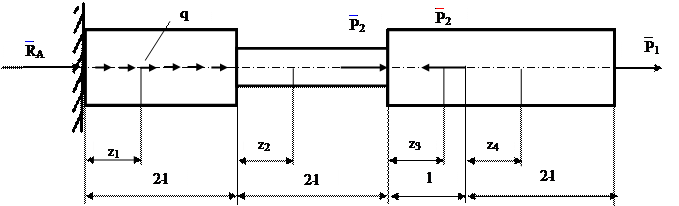
Рассмотрим пример построения эпюр внутренних силовых факторов для плоской рамы, нагруженной сосредоточенной силой, моментом и равномерно распределенной нагрузкой.

Задача
Построить эпюры внутренних продольных и поперечных усилий и изгибающих моментов для плоской П-образной рамы, нагруженной силой F, моментом m и распределенной нагрузкой q:

Решение
Рама состоит из трех частей (левая и правая вертикальные стойки соединенные горизонтальным ригелем), но при этом имеет четыре силовых участка – AC, CD, BE и DE, на каждом из которых нам потребуется определить величину и направление внутренних усилий.

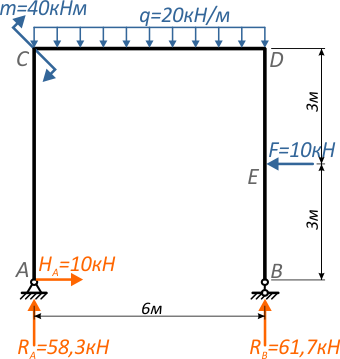
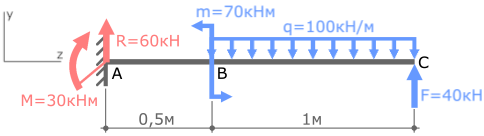
Для заданной расчетной схемы рамы ранее мы уже определили опорные реакции.

Расчет значений

Обозначим силовые участки римскими цифрами.

Для расчета значений, необходимых для построения эпюр, будем пользоваться методом сечений и соответствующими правилами знаков.

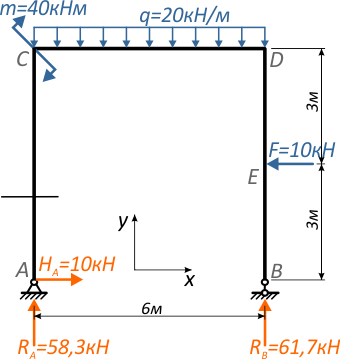
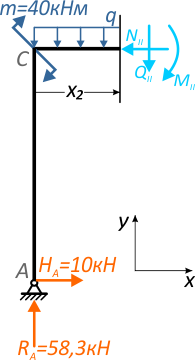
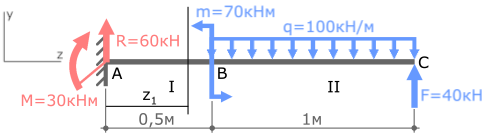
Начинаем с первого силового участка AC.

Мысленно рассекаем его в любом месте между крайними точками участка.

Это сечение делит раму на две части:

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Можно рассмотреть любую из них, но для упрощения расчетов рекомендуется выбирать менее нагруженную часть конструкции.

Очевидно, что в данном случае проще рассматривать нижнюю часть стойки.

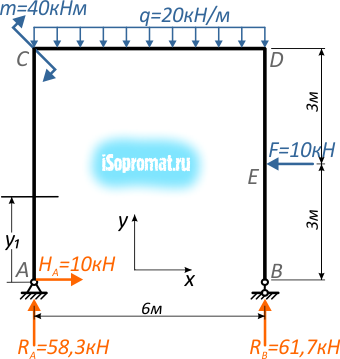
Расстояние от границы участка до сечения обозначим переменной y₁, возможные значения которой находятся в пределах от нуля до длины участка.

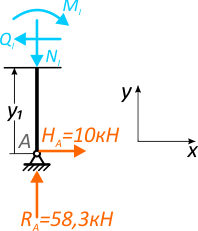
Действие отброшенной части рамы заменим внутренними усилиями N_I, Q_I и M_I.

Рассчитаем их: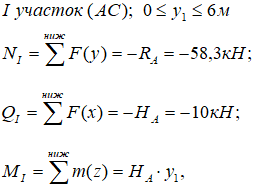

В выражении для M_I переменная y₁ в первой степени, а значит, эпюра на этом участке будет изображаться прямой. Для ее построения необходимы значения в двух точках.
Рассчитаем их на границах участка, в точках A и C: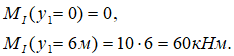

В записанных выражениях:
N_I – по правилу знаков для внутренних продольных сил – отрицательна, т.к. на участке имеет место сжатие;
Q_I – отрицательна, т.к. стремится повернуть рассматриваемую часть рамы против хода часовой стрелки;
Для изгибающих моментов M будем отмечать то, какие слои они стремятся сжать. В данном случае момент M_I сжимает правую сторону стойки.

Расчет значений внутренних силовых факторов для остальных участков рамы выполняется аналогично.

На втором участке, проведя сечение (рис. 7), выберем для рассмотрения левую часть рамы (левая часть ригеля со стойкой AC).

Продольную силу N_II здесь вызывает горизонтальная реакция H_A, которая сжимает ригель.
Поперечную силу Q_II в сечении дают реакция R_A и распределенная нагрузка q.
Изгибающий момент M_II создается всеми нагрузками расположенными слева от рассматриваемого сечения.
Опорные реакции R_A и H_A создают момент силы. Для момента создаваемого силой H_A плечо одинаково для любого положения сечения, и равно длине стойки AC, для момента реакции R_A плечо переменное (y₂).
О том, как рассчитать момент, создаваемый распределенной нагрузкой q можно прочитать здесь.

Записываем выражения: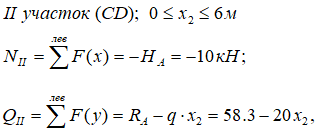

это уравнение прямой, поэтому рассчитаем значения на границах участка: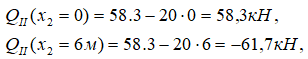

Сразу следует обратить внимание, что значения на границах участка имеют противоположные знаки, т.е. эпюра Q на данном участке пересекает базовую (нулевую) линию, следовательно, на эпюре моментов M_II в этом сечении будет экстремум (эпюры Q и M дифференциально зависимы).

Запишем выражение для изгибающих моментов: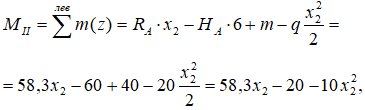

получили уравнение параболы, для построения которой требуется минимум три точки.

Двумя из них будут граничные значения момента: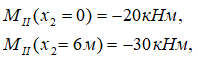

Третьей станет значение экстремума эпюры M на участке.

Короткое видео про расчёт экстремума эпюры изгибающих моментов:

Рассчитаем его:
Выражение для Q_II приравниваем к нулю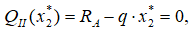

откуда находим координату сечения рамы, где Q пересекает базовую линию.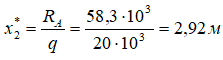

подставляем ее в выражение для M_II и находим значение экстремума.

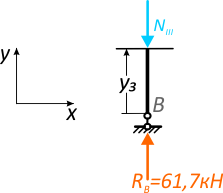
Для третьего участка рамы выбираем нижнюю часть (рис. 7):

Записываем выражения: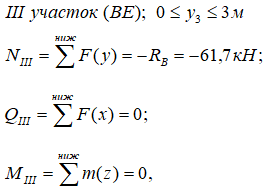

Здесь имеется только продольная сжимающая сила.

На четвертом участке (рис. 7) тоже рассмотрим нижнюю часть стойки

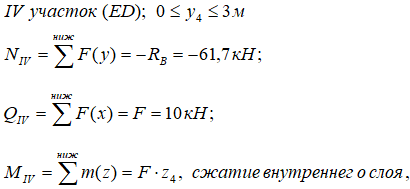
Граничные значения изгибающего момента

Расчет значений окончен, переходим к графическим построениям.

Построение эпюр

Для горизонтальных и вертикальных участков рамы положительные значения эпюр продольных N и поперечных сил Q будем откладывать соответственно вверх и вправо.

Как строить эпюры по рассчитанным значениям показано в нашем видео:

Эпюра внутренних продольных сил N:
Эпюра внутренних продольных сил N рамы

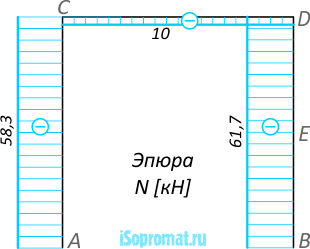
Эпюра внутренних поперечных сил Q:
Эпюра внутренних поперечных сил Q рамы

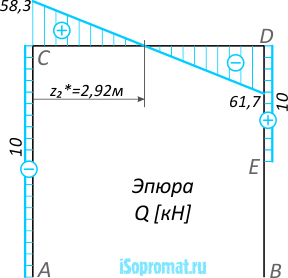
Эпюра изгибающих моментов M строится на сжатых волокнах рамы:
Эпюра внутренних изгибающих моментов M рамы

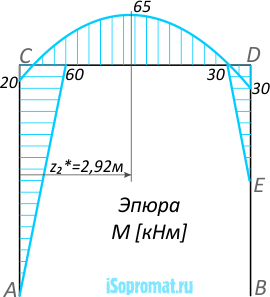
Эпюры внутренних силовых факторов для рамы построены.
Теперь необходимо выполнить их проверку.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Построение эпюр

Вы будете перенаправлены на Автор24

Эпюру можно построить на основании следующих параметров: внутренних сил (продольных и поперечных), крутящих и изгибающих моментов, напряжений (нормальных и касательных) и перемещений.

Процесс построения эпюр

Процесс построения эпюры стандартизирован и осуществляется по определенным правилам. Это сделано для общего понимания графиков всеми участниками производственного процесса.

Затем определяются границы силовых участков, то есть таких участков, где силовой фактор (деформация) остается постоянным или изменяется в рамках одной закономерности. Зачастую, границы силовых участков представляют собой сечения с приложенной внешней нагрузкой. Обозначение границ на эпюре реализуется в виде тонких вертикальных линий.

Если брус обладает сложной объемной формой, то границы определяют аналитически.

Далее эпюра масштабируется. Масштаб выбирается в соответствии с предварительным просчетом отображаемого фактора по всем контрольным сечениям (КС) бруса.

После выбора масштаба и построения внешнего контура эпюры КС присваиваются значения фактора без указания знака (“$+$” и “$–$”). Факторы с положительными значениями чертятся над нулевой линией, а с отрицательными под.

В области с положительными значениями на самом широком участке пишется знак “$+$” и обводится кружком, а с отрицательными выполняется также операция, но указывается знак “$–$”. Можно поставить знаки справа и слева от “$0$”, при этом кружками они обводится не будут.

Готовые работы на аналогичную тему

Определение знака фактора

Знак фактора определяется направлением внутренних силовых факторов и действием деформации. Например, нагрузке продольного типа, направленной на сжатие присваивается знак “$–$”, а на растяжение “$+$”.

Пример построения

Начертим расчетную схему и укажем все нагрузки и значения:

Рисунок 1. Расчетная схема двухопорной балки. Автор24 — интернет-биржа студенческих работ

Определим реакции опор ($R$) в данном случае реакция для каждой точки будет равна половине приложенной, силы, так части балки равны по длине (нагрузка распределена).

Обозначаем границы участков балки.

Рисунок 3. Границы участков балки. Автор24 — интернет-биржа студенческих работ

Рисунок 4. Произвольное сечение D. Автор24 — интернет-биржа студенческих работ

$Qy_1 = Ra = 10 кН$

Обозначим границы, указав значение поперечной силы на графике, и начертим эпюру.

Рисунок 5. Эпюра поперечной силы. Автор24 — интернет-биржа студенческих работ

Запишем уравнение для изгибающего момента. В данном случае момент силы направлен на растяжение, поэтому укажем знак “$+$”, поэтому уравнение имеет вид:

Изображение эпюров со стороны растянутых волокон (показано в примере) характерно для инженерно-строительной практики. В механике эпюра чертится со стороны сжатых волокон.

$Mx_1(z_1 = 0) = Ra • z_1 = 5 • 0 = 0$

$Mx_1 (z_1 = 4) = Ra • z_1 = 5 • 4 = 20$

Рисунок 6. Эпюра изгибающего момента. Автор24 — интернет-биржа студенческих работ

Выполним расчеты для второго участка балки:

$Qy_2 = – Rb = –10 кН$

$Mx_2 (z_2 = 0) = Rb • z_2 = 5 • 0 = 0$

$Mx_2 (z_2 = 4) = Rb • z_2 = 5 • 4 = 20$

Начертим окончательную версию эпюры.

Рисунок 7. Полноценная эпюра рассматриваемой балки. Автор24 — интернет-биржа студенческих работ

Нужны еще материалы по теме статьи?

Воспользуйся новым поиском!

Найди больше статей и в один клик создай свой список литературы по ГОСТу

Автор этой статьи Дата последнего обновления статьи: 27.03.2022

Виктория Валерьевна Колесникова

Эксперт по предмету «Сопротивление материалов»

Источник

iSopromat.ru

Построение эпюр

Примеры построения эпюр для решения задач сопротивления материалов, строительной и технической механики со всеми расчетами, подробными пояснениями и видеоуроками.

Примечание: студентам строительных специальностей эпюры изгибающих моментов надо строить на растянутых слоях балки, поэтому положительные значения Mx необходимо откладывать вниз, а отрицательные — вверх от базовой линии.

Рассмотрим пару упрощенных и несколько максимально подробных примеров построения эпюр внутренних силовых факторов, напряжений и перемещений для всех способов закрепления и нагружения балок, стержней и валов.

Построение эпюр Q_y и M_x для консольной балки

Для заданной консольной балки требуется построить эпюры внутренних силовых факторов Q_y и M_x.

Решение

Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.

Показываем оси системы координат y-z и обозначаем характерные сечения балки.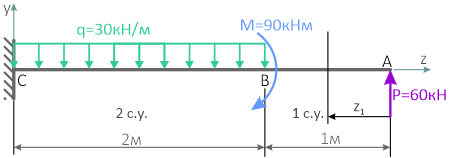

Для построения эпюр внутренних силовых факторов консольных балок, опорные реакции можно не определять.

Тогда для расчета значений Q_y и M_x необходимо рассматривать противоположную от заделки часть балки, где все внешние усилия известны.

Балка имеет 2 силовых участка.

Рассчитаем, с учетом правил знаков при изгибе, значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.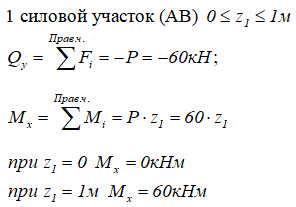

На первом участке оба силовых фактора рассчитаны.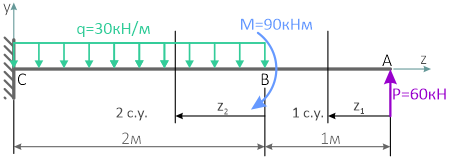

Переходим ко второму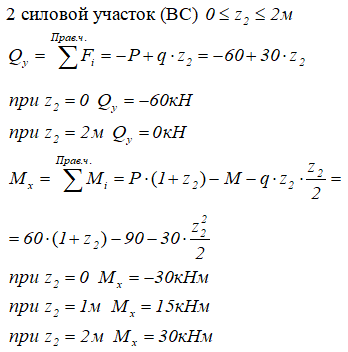

Так как эпюра Q_y на втором силовом участке не пересекает базовую линию, экстремума на эпюре M_x не будет.

По полученным данным строим эпюры внутренних поперечных сил Q_y и изгибающих моментов M_x.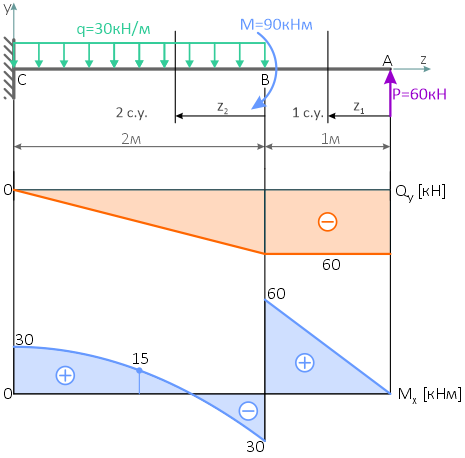

При ручном оформлении решения, эпюры заштриховываются тонкими линиями перпендикулярно базовой (нулевой) линии.

Оформление в электронном виде допускает сплошную однородную заливку площади эпюры.

Проверка построенных эпюр:

Все условия выполнены, следовательно, эпюры построены верно.

Построение эпюр для балки на двух опорах

Для заданной расчетной схемы балки на двух шарнирных опорах требуется построить эпюры внутренних поперечных сил и изгибающих моментов.

Решение

При построении эпюр для участков балки расположенных между опорами необходимо знать величину хотя бы одной из реакций.

Определение реакций в шарнирных опорах балки

Направим реакции опор, например, вверх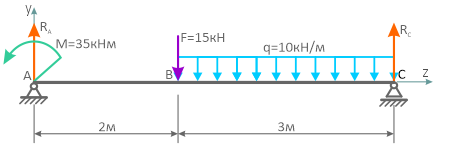

и запишем, с учетом правила знаков, суммы моментов нагрузок приложенных к балке относительно точек на опорах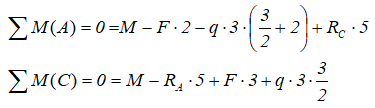

Из составленных уравнений выражаем и находим реакции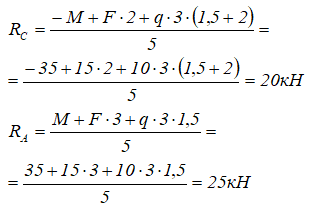

Положительные значения указывают на то, что произвольно заданное направление реакций оказалось верным.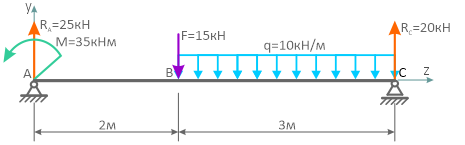

Расчет и построение эпюр

Используя метод сечений и соответствующие правила знаков, рассчитаем по каждому участку значения для построения эпюр.

Балка имеет 2 силовых участка.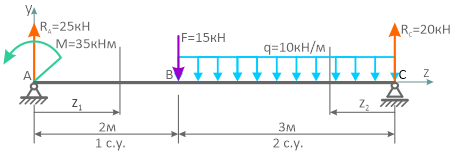

На первом участке расчет произведем, рассматривая левую отсеченную часть балки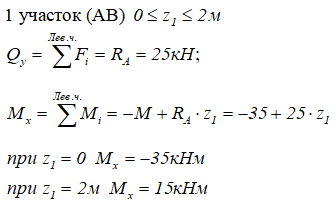

На втором — правую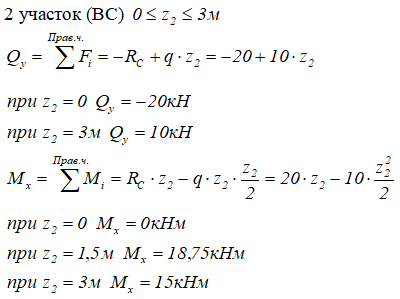

Значения поперечной силы Q_y на границах участка имеют разные знаки, следовательно, на этом участке, на эпюре M_x будет экстремум.

Определим его: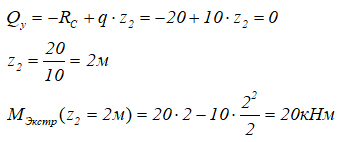

По полученным данным строим эпюры внутренних поперечных сил и изгибающих моментов.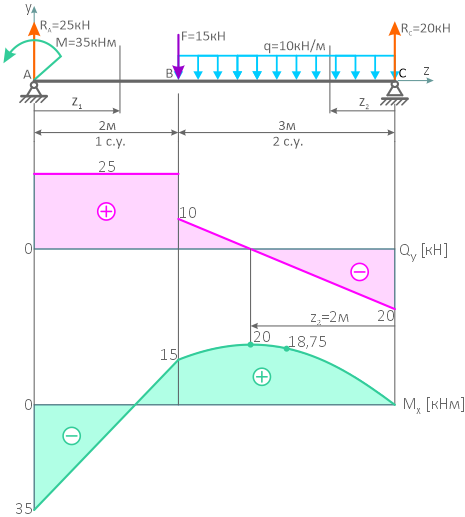

Алгоритм проверки эпюр показан в решении предыдущей задачи.

Более подробно ход расчетов и построения эпюр для балки с тремя силовыми участками рассмотрен в следующих задачах.

Подробные примеры построения эпюр

При растяжении-сжатии

Примеры построения эпюр внутренних продольных сил, нормальных напряжений и линейных перемещений для стержней при их растяжении и сжатии.

При кручении

Примеры построения эпюр внутренних крутящих моментов и угловых перемещений сечений вала при кручении.

Построение эпюр при изгибе

Примеры построения эпюр внутренних поперечных сил и изгибающих моментов, нормальных и касательных напряжений для балок и рам при изгибе.

Эпюры внутренних силовых факторов

Эпюры напряжений

Видеоурок расчетов для построения эпюр внутренних силовых факторов для балки:

Порядок построения эпюр

В рассмотренных выше примерах для построения эпюр выполняется следующая последовательность действий:

После построения эпюр желательно выполнять их проверку.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Эпюры: поперечных сил и изгибающих моментов

В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.

В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.

Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.

Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.

Поперечные силы и изгибающие моменты

При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (M_изг).

Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.

Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.

Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!

Обозначения поперечных сил и изгибающих моментов

Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.

Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Q_y (параллельна оси y), а изгибающий момент, как M_x (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Q_y, M_z или Q_z, M_x. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – M_изг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.

Расчётная схема балки

Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.

К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.

Правила знаков для поперечных сил и изгибающих моментов

В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).

Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и М_изг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).

Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.

Правило знаков для поперечных сил

Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:

Правило знаков для изгибающих моментов

Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.

На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.

Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:

Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:

Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:

В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.

Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉

Построение эпюр для консольной балки

В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.

Рассмотрим первый участок

Обозначим некоторое сечение 1-1 на расстоянии x₁, от свободного торца балки, при этом x₁ будет находиться в диапазоне: 0 ≤ x₁ ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.

Поперечные силы на первом участке

Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:

Как видишь, поперечная сила будет постоянна на первом участке:

Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке

Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:

Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка

Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x₂ от начала участка (0 ≤ x₂ ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке

Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:

Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке

Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:

Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр

Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.

Определение реакций в жёсткой заделке

Расчёт эпюр поперечных сил и изгибающих моментов

Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.

Эпюра моментов со стороны растянутых или сжатых волокон

По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.

Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.

Учёт распределённой нагрузки

Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.

Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A

Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.

После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила Q_A будет равна:

Изгибающий момент M_{изг, A} будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов

Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:

Рассчитаем значения на эпюре поперечных сил:

Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:

На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.

Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

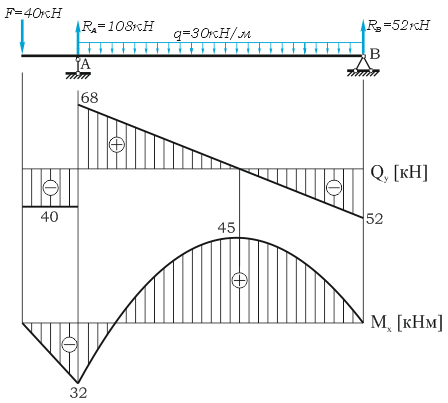
Построение эпюр для двухопорной балки

А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:

Строим эпюры на первом участке:

Определение экстремума на эпюре моментов

Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.

Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:

Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках

Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:

Оценка правильности построенных эпюр поперечных сил и изгибающих моментов

И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.

Вот несколько признаков, правильно построенных эпюр:

1 комментарий

Опубликовал новую статью по построению эпюр для балок. Позднее планирую добавить в статью примеры по построению эпюр для плоских рам. Если будут какие-нибудь вопросы по уроку, можешь спросить здесь.

Источник

Техническая механика

Сопротивление материалов

Построение эпюр в сопромате

Прикладное значение науки сопротивление материалов заключается в возможности определения основных критериев работоспособности деталей машин и различных конструкций – прочности, деформации и устойчивости.
Применяя метод сечений в сочетании с приемами статики и других разделов прикладной механики, можно определить напряжения, возникающие в том или ином сечении бруса (детали, элемента конструкции), и, исходя из анализа полученного результата, сделать выводы о работоспособности этого бруса при приложении к нему расчетных нагрузок.
Именно напряжение является основным фактором, влияющим на прочностные характеристики элемента конструкции, а также его способность противостоять деформации. По этой причине в сопромате главной задачей, чаще всего, является определение напряжений, возникающих в том или ином сечении детали или элемента конструкции.

Для удобства анализа напряженности отдельных участков и сечений конструкции (бруса) используют графическое изображение нагрузок и напряжений в каждом сечении. Это позволяет визуально анализировать распределение нагрузок и напряжений по всей длине бруса, определять при этом наиболее нагруженные (критические) участки и сечения. Такие графические изображения нагрузок, напряжений, а также деформаций элементов конструкций называют эпюрами.

При анализе степени напряженности и деформирования элемента конструкции (детали, бруса) наиболее часто производят построение следующих типов эпюр:

Иногда на одной эпюре показываются несколько внутренних силовых факторов (эпюра продольных и поперечных сил, эпюра изгибающего и вращающего моментов), но такие эпюры при сложных нагрузках и переменных сечениях бруса сложны для чтения.

Как упоминалось выше, наиболее важную информацию о прочностных характеристиках элемента конструкции (бруса), т. е. способности противостоять разрушению, можно получить, используя эпюры напряжений, а информацию о степени деформации под действием расчетной нагрузки – по эпюрам перемещений.
Эпюры внутренних усилий и моментов в большинстве случаев не дают полной информации о степени напряженности и деформирования отдельных сечений и участков бруса, а являются промежуточным звеном при построении эпюр напряжений и перемещений, особенно если брус имеет ступенчатую форму или переменное поперечное сечение по длине.

Правила построения эпюр

При построении эпюр придерживаются определенных стандартных правил, позволяющих одинаково читать, истолковывать и анализировать эпюру всем участникам процесса конструирования изделия.

Построение эпюры начинают с изображения нулевой линии, которая символизирует линию бруса в ненапряженном состоянии. При этом, если брус имеет сложную пространственную форму, нулевая линия эпюры повторяет контуры центральной (осевой) линии бруса, и имеет такую же пространственную форму.

Нулевую линию эпюры обозначают названием и нулевым символом. Слева от нулевой линии указывается название эпюры (эпюра сил, моментов, напряжений и т. п.), справа от нулевой линии ставится цифра « 0 ». При указании называния эпюры обычно используют символ изображаемой нагрузки, например, внутренние продольные силы чаще всего обозначаются буквой « N », поперечные – буквой « Q », эпюры изгибающих моментов – буквами « M_из », эпюры вращающих моментов – буквами « Т » или « M_кр », эпюры напряжений – буквами « σ » или « τ » и т. п. Рядом с буквенным названием эпюры (или под ним) указывается единица измерения (ньютон, мегапаскаль, мм и т. п.).

Следующий этап построения эпюры – определение границ силовых участков бруса, т. е. таких участков, где внутренний силовой фактор в сечениях или деформация бруса изменяются по одной закономерности (или остаются постоянными). Как правило, границами силовых участков являются сечения, где приложена внешняя нагрузка или (и) площадь поперечного сечения бруса изменяется. В некоторых случаях, при построении эпюр брусьев сложной объемной формы, границы участков определяют аналитически. Границы силовых участков обозначаются тонкими вертикальными линиями, проведенными от изображения бруса через все эпюры.

Для оптимальной наглядности графика эпюры важно правильно выбрать масштаб изображаемого силового фактора, напряжения или деформации. Если масштаб окажется слишком мелким – эпюра будет трудна для чтения и анализа, если слишком крупным – она займет много места на чертеже.
Если учесть, что для одного бруса выполняют, как правило, несколько эпюр, расположенных одна под другой, то крупный масштаб не позволит выполнить построение эпюр на одном листе.
Для правильного выбора масштаба эпюры предварительно следует просчитать значение отображаемого фактора по всем контрольным сечениям бруса, и после этого определиться с масштабом.
Если, например, в результате расчетов окажется, что вся эпюра займет положительную область (над нулевой линией), то при построении графика эпюры это следует учесть.

Положительные значения фактора откладываются вверх от нулевой линии, отрицательные – вниз. Если на каком-либо участке силовой фактор равен нулю, эпюра совпадает с нулевой линией по всей длине этого участка. После построение внешнего контура эпюры на контрольных сечениях проставляются значения фактора (обычно на внешних углах эпюры), при этом знак фактора (плюс или минус) не указываются.
На положительной области (в самой широкой части) ставится знак «+» в кружке, а на отрицательной области – знак «—» в кружке (см. примеры построения эпюр). Иногда знаки «+» и «—» на эпюре указываются сверху и снизу цифры « 0 » (справа нулевой линии), тогда на площади графика эпюры эти знаки (в кружках) не ставятся.

По окончании построения эпюры по ее площади проводят тонкие вертикальные линии через равные промежутки. Эти линии символизируют сечения бруса. Иногда, в случае построения сложной пространственной эпюры, линии выполняют не вертикально, а в соответствии с проекционным направлением участка на графике эпюры.

Определение знака фактора на эпюре

При построении эпюр внутренних силовых факторов или деформаций необходимо правильно определять знак фактора на данном силовом участке бруса. Для этого следует пользоваться следующими общепринятыми правилами:

Особенности построения эпюр поперечных сил и изгибающих моментов

Для облегчения построения эпюр и контроля правильности графика следует запомнить ряд правил, вытекающих из теоремы Журавского:

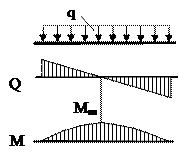
На участке, где равномерно распределенная нагрузка q отсутствует, эпюра поперечных сил Q представляет собой прямую линию, параллельную нулевой линии (оси бруса), а эпюра изгибающих моментов M_из – наклонную прямую.

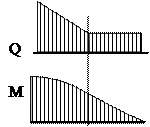
В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть ступенчатый скачок на величину этой силы, а на эпюре M_из – излом (изменение направления графика).

На участке действия равномерно распределенной нагрузки q эпюра Q представляет собой наклонную прямую, а эпюра M_из – параболу, обращенную выпуклостью навстречу стрелкам, изображающим направление распределенной нагрузки.

Если эпюра Q на наклонном участке в каком-либо сечении пересекает нулевую линию эпюры, то в этом сечении на эпюре изгибающих моментов M_из будет иметь экстремальное значение (минимальное или максимальное).

Если на границе действия распределенной нагрузки нет сосредоточенных сил, то наклонный участок эпюры Q соединяется с горизонтальным без «ступеньки», а параболический участок эпюры M_из соединяется с наклонным участком плавно, без излома.

В сечениях, где к брусу приложены сосредоченные пары сил, на эпюре M_из будут иметь место ступенчатые скачки на величину действующих внешних моментов, а эпюра Q изменения не претерпевает (приложенные к брусу изгибающие моменты не влияют на эпюру поперечных сил).

Примеры построения эпюр

Материалы раздела «Сопротивление материалов»:

Источник

iSopromat.ru

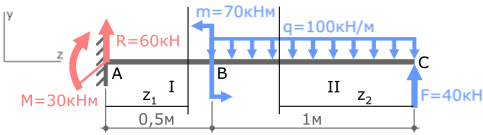
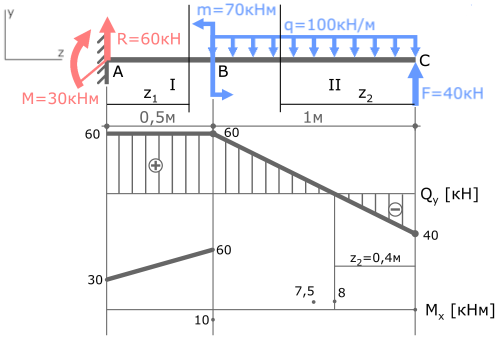
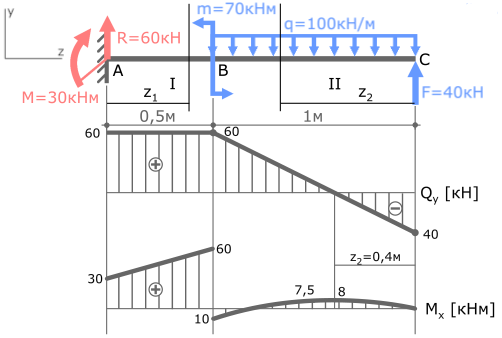
Пример решения задачи на построение эпюры внутренних изгибающих моментов M_x для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Пример решения

Покажем найденные опорные реакции и выбранную систему координат.

Для построения эпюры изгибающих моментов M_x запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

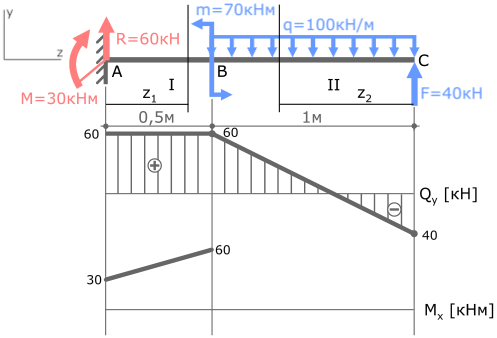
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Q_y.

Рассмотрим I силовой участок:

Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.

Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.

Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.

По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:

В выражении переменная z₁ в первой степени, поэтому эпюра M_x на первом участке будет иметь вид прямой линии.

Рассчитаем значения M_xI на границах участка, т.е. при z₁=0 и при z₁=0,5м

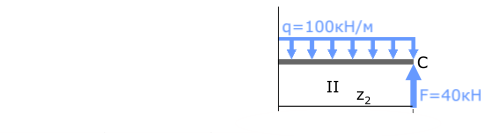
Переходим на второй силовой участок:

Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.

Получено выражение с переменной z₂ во второй степени, значит, эпюра M_x на втором участке будет иметь вид параболы.

Видео про построение эпюр:

Для построения параболы требуется как минимум три точки. Этими точками будут значения M_x на границах и в середине II силового участка, то есть при z₂=0, z₂=1м и z₂=0,5м.

По полученным данным строим эпюру изгибающих моментов M_x (готовую эпюру Q_y перенесем из ранее рассмотренной задачи)

Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Q_y.

Q_y — первая производная от M_x. Поэтому в том месте, где Q_y пересекает базовую линию (т.е. Q_y=0) на эпюре M_x будет экстремум.

Видео про расчет экстремума эпюры:

Рассчитаем значение экстремума эпюры M_x на II участке балки.

Отметив эту точку в области эпюры где Q_y=0 соединим ее с тремя другими параболой.

Эпюра изгибающих моментов построена. Проверка эпюры M_x.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

iSopromat.ru

Эпюрами в сопротивлении материалов называют графическое представление данных о распределении соответствующих факторов по длине либо сечению рассматриваемого бруса.

а также напряжений и перемещений.

Они наглядно показывают нагруженность участков бруса, положение опасных, с точки зрения прочности, точек сечения, а также направление и величину перемещения сечений.

Для их построения используется метод сечений:

Полученные значения откладываются в виде точек от базовой (нулевой) линии в соответствии с их знаком, затем точки соединяются согласно функции определяющей их величину на каждом участке.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Методика построения эпюр изгибающих моментов, поперечных и продольных сил

1. Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При решении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых

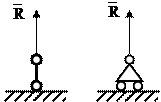
наиболее часто встречаются: шарнирно-подвижнаяопора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

2. Построение эпюр продольных сил N z

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Пример 1.Построить эпюру продольных сил для жестко защемленной балки (рис.2).

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.

По найденным значениям строимэпюру Мкр (рис.3,б).

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры Nz и Мкр всегда прямолинейные.

3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.

5. Построение эпюр поперечных сил Q y и изгибающих моментов M x в балках

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Схематически это правило знаков можно представить в виде

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.

6. Консольные балки

При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3.Построить эпюры Qy и Mx (рис.4).

1. Намечаем характерные сечения.

2. Определяем поперечную силу Qy в каждом характерном сечении.

По вычисленным значениям строим эпюру Qy.

3. Определяем изгибающий момент Mx в каждом характерном сечении.

По вычисленным значениям строим эпюру Mx, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

7. Балки на двух опорах

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:

Пример 4. Построить эпюры Qy, Mx для балки с шарнирным опиранием (рис.5).

1. Вычисляем реакции опор.

2. Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

Строим эпюру Qy.

4. Определяем изгибающие моменты в характерных сечениях.

Строим эпюру Mx.

8. Правила контроля эпюр Q у и M x

Дифференциальные зависимости между q, Qy, Mx определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.

Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.

Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy=0), то эпюра Mx в этом сечении имеет экстремум.

На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy>0 эпюра Mx возрастает слева направо; при Qy

Источник

iSopromat.ru

Эпюрами внутренних усилий в балках называют геометрические образы, применяемые для графического изображения изменения в элементе какого-либо силового фактора либо иных данных.

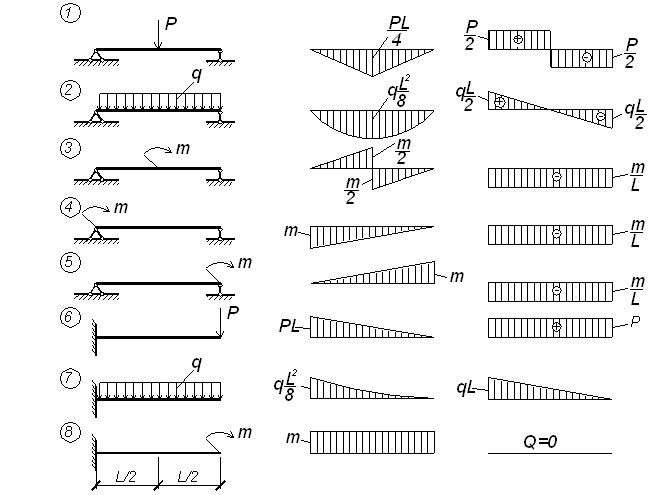
Эпюры внутренних усилий (поперечных сил и изгибающих моментов) для простейших систем показаны на рисунке 3.1.

Рисунок 3.1 – Эпюры внутренних усилий для простейших балок

Отметим, что в строительной механике, на эпюре изгибающих моментов знак, как правило, не ставится, и в отличие от сопромата, она строится со стороны растянутых волокон.

Эпюры для однопролетных балок с консолями строят в следующем порядке:

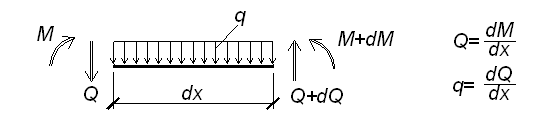
Между выражениями для изгибающего момента, поперечной силы и интенсивностью распределенной нагрузки в пределах расчетного силового участка существуют известные из курса «Сопротивление материалов» дифференциальные зависимости.

Они легко выводятся с помощью уравнений равновесия, составленных для вырезанного бесконечно малого элемента (рисунок 3.2):

Рисунок 3.2 – Определение значений поперечной силы

Внутренние силы в основных типах элементов систем:

Понятие о расчетном силовом участке

Расчетным силовым участком называется участок элемента системы с постоянным законом изменения всех внутренних силовых факторов.

В расчетной практике силовые участки определяются их границами.

Граница силового участка − это место приложения какой-либо сосредоточенной нагрузки (силы или момента), начало или конец распределенной нагрузки, место изменения геометрии, механических характеристик конструкции, интенсивности распределенной нагрузки.

В курсе «Строительная механика» принята следующая последовательность определения внутренних усилий (построения эпюр).

Первоначально с помощью уравнений статики в требуемых сечениях определяются изгибающие моменты.

Далее посредством дифференциальной зависимости осуществляется переход к поперечным силам. Последние дают возможность оценить и продольные силы.

Построение эпюры моментов производится по силовым участкам. При этом за расчетный модуль принимается консольная балка (рисунок 3.3).

За начало (В) принимается тот конец силового участка, на котором все внутренние и внешние воздействия определены.

Рисунок 3.3 – Консольная балка

Они (воздействия) легко (принцип независимости действия сил) приводятся к алгебраической сумме результатов простейших воздействий.

При построении эпюр внутренних усилий в многопролетных балках, рамах и других конструкциях используются эпюры М и Q в простых однопролетных и консольных балках, которые чаще всего называют табличными эпюрами моментов и поперечных сил (рисунок 3.1).

Последовательность построения эпюр внутренних усилий М, Q, N в статически определимых системах:

2) Определение опорных реакций и реакций связи. При этом используются уравнения равновесия, составленные как для всей системы в целом, так и для любого элемента или группы элементов.

По эпюре изгибающих моментов с помощью дифференциальной зависимости Журавского строится эпюра поперечных сил (Q).

На участке с линейной эпюрой изгибающих моментов величина поперечной силы равна тангенсу угла наклона эпюры М.

Q = |tga| — где a угол наклона касательной на эпюре М к оси балки.

Знак Q определяется по направлению кратчайшего совмещения оси участка с эпюрой. Если оно происходит по направлению движения часовой стрелки, поперечную силу считают положительной.

Если же против часовой стрелки, то отрицательной.

При построении эпюры поперечных сил для участков с криволинейной (изменяющейся только по закону квадратной параболы) эпюрой изгибающих моментов пользуются следующей зависимостью:

где Q_о − поперечная сила от внешней нагрузки, приложенной на рассматриваемый участок, определенная для балки на двух опорах пролета равного L;

М_п, М_л − алгебраические величины изгибающих моментов, соответственно на правом и левом торцах рассматриваемого участка.

Вышеуказанное выражение (3.1) легко получить самостоятельно (рисунок 3.4):

Рисунок 3.4 – Вывод выражения (3)

4) По эпюре поперечных сил строится эпюра продольных сил. При этом рассматривается равновесие всех узлов системы под действием внутренних (продольных и поперечных) и внешних (узловых) сил.

Правила для проверки правильности построенных эпюр внутренних усилий:

а) На прямолинейном ненагруженном участке эпюра моментов прямолинейна.

б) В сечении, где приложен сосредоточенный внешний момент, эпюра получает скачок на величину этого момента (рисунок 3.5), а линии эпюры моментов примыкающие к скачку идут параллельно друг другу.

Рисунок 3.5 – Эпюра М на участке с приложенным сосредоточенным моментом

в) В точке приложения сосредоточенной внешней силы Р, перпендикулярной оси стержня, эпюра моментов имеет перелом, направленный острием в сторону действия силы (рисунок 3.6).

Изменение тангенсов углов наклона эпюры в точке ее перелома равно силе Р. На эпюре Q в этой точке — скачок на величину Р в направлении ее действия.

Рисунок 3.6 – Эпюра М на участке с приложенной сосредоточенной силой Р

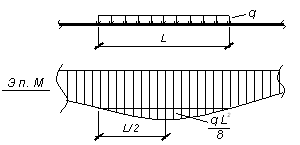
г) На участке, где приложена равномерно распределенная нагрузка, эпюра моментов очерчена по параболе второй степени с выпуклостью в сторону действия нагрузки и со стрелкой равной q×L 2 /8 (рисунок 3.7).

Рисунок 3.7 – Эпюра М на участке с равномерно распределенной нагрузкой

д) В сечениях, где нет сосредоточенной нагрузки, эпюра моментов не имеет перелома.
е) Поперечная сила в сечении стержня положительна, если она стремится вращать разделенные данным сечением части стержня по часовой стрелке (рисунок 3.8).

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

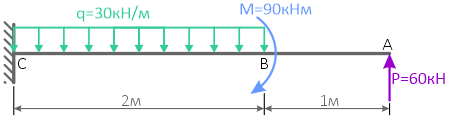
Построение эпюр поперечных сил и изгибающих моментов

Для расчета балки на прочность при изгибе необходимо знать наибольшие значения поперечной силы Q_y и изгибающего момента M_z и положение сечений, в которых они действуют. В связи с этим возникает необходимость определения законов изменения Q_y и M_z по длине балки. Для этой цели обычно строят эпюры поперечных сил и изгибающих моментов, которые представляют собой графическое изображение функций Q_y(x) и M_z(x).

Примем положительное направление оси Оу вниз. При этом на эпюре Q_y положительные ординаты будем откладывать вниз, а отрицательные — вверх. Ординаты эпюры M_z будем откладывать со стороны растянутых волокон балки. Согласно этому правилу для балок положительные значения изгибающих моментов откладываются вниз, так как эти моменты вызывают растяжение нижних волокон.

Рассмотрим примеры построения эпюр Q_y и M_z.

Пример 7. /. Построим эпюры Q_y и M_z для шарнирно опертой балки, показанной на рис. 7.14.

Из уравнений статики найдем опорные реакции:

Установим законы изменения Q_y и M_z на участках АС и СВ балки.

На участке АС (0 = 0 и J]М_В = 0 выполняются. Следовательно, узел В находится в равновесии.

Пример 7.11. Для стержня с криволинейным участком в виде четверти окружности (рис. 7.27, а) построим эпюры внутренних усилий N, Q и М.

Определим опорные реакции:

Определим с помощью метода сечений законы изменения внутренних усилий на криволинейном участке (рис. 7.26). Приравнивая к нулю сумму проекций всех сил по направлению нормали и касательной к сечению, а также сумму моментов относительно центра тяжести сечения, получим:

Вычислим значения внутренних усилий в характерных сечениях горизонтального участка АС.

Откладывая вычисленные значения в рассмотренных сечениях перпендикулярно к оси стержня и соединяя полученные точки, построим эпюры внутренних усилий N, Q и М. Эти эпюры приведены на рис. 7.27, б, в, г.

Поперечная сила Q на прямолинейном участке АС обращается в нуль в сечении на расстоянии х₀ от точки А. В этом сечении изгибающий момент принимает экстремальное значение. Из подобия треугольников на эпюре Q определим

Вычислим экстремальное значение изгибающего момента:

Пример 7.12. Для балки с наклонным участком (рис. 7.28, а) построим эпюры N, Qm М.

Определим опорные реакции:

При определении продольной и поперечной сил в пределах наклонного участка надо нагрузку и опорные реакции проектировать на ось стержня и на нормаль к оси.

Источник

Построение эпюры материалов

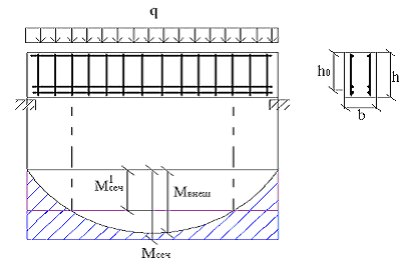
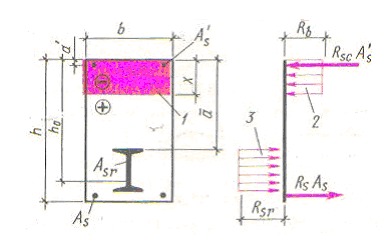
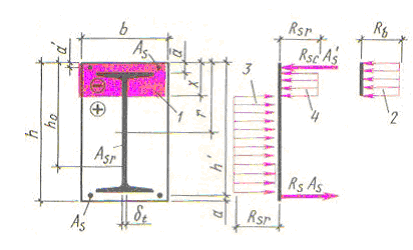
Эпюра материалов – это эпюра изгибающих моментов, выдерживаемых сечением элемента.

Эпюра материалов наглядно показывает для каждого сечения элемента превышение величины изгибающего момента, соответствующего площади сечения арматуры, по сравнению с его теоретическим значением.

Рис. 11.14. Построение эпюры материалов

Порядок определения места фактического обрыва продольных стержней в пролете следующий:

1. На эпюру моментов 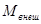от внешних нагрузок (см. рисунок 11.14.) наносят ординаты момента, воспринимаемого нормальным сечением элемента с продольной арматурой, которую доводят до торца элемента (т.е. несущая способность данного сечения).

2. Точки пересечения эпюры расчетных моментов с эпюрой обрываемой арматуры определяет места теоретического обрыва стержней. Места действительного обрыва стержней отстоят от теоретической точки на величину 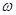, которая определяется как:

Рис. 11.19. Эпюра материалов

Чем ближе эпюра моментов фактически установленной продольной арматуры примыкает к теоретической огибающей эпюре моментов, тем большую получают экономию арматуры.

С этой целью рекомендуется в растянутой зоне изгибаемых элементов устанавливать не менее 4 стержней, чтобы 2 из них можно было оборвать в пролете. Высоту сжатой зоны определяют из условия равновесия проекций усилий в бетоне и арматуре наклонного сечения на продольную ось элемента, т.е.:

При наличии отгибов несущая способность будет следующей:

По СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры» по п.6.2.33. расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия 6.65

Расчет изгибаемых элементов по наклонному сечению на действие поперечных сил (п. 6.2.34) производят из условия 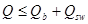, причем поперечную силу Q_b определяют по формуле 6.67

Усилие Q_sw для поперечной арматуры определяют по формуле 6.68

Расчет железобетонных элементов по наклонным сечениям на действие моментов производят по п. 6.2.35.

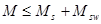
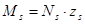
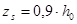
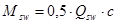
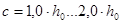
По формуле 6.73 , при этом (допускается принимать ), а ()

Конструктивные требования

1. Анкеровка ненапрягаемой арматуры

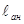
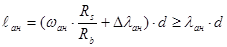
По п.5.14 СНиП 2.03.01-84* «Бетонные и железобетонные конструкции» продольные стержни растянутой и сжатой арматуры должны быть заведены за нормальное к продольной оси элемента сечение, в котором они учитываются с полным расчетным сопротивлением, на длину не менее , определяемую по формуле

(11.7)

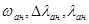
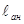
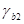
где значения , а также допускаемые минимальные величины определяются по табл. 37. При этом гладкие арматурные стержни должны оканчиваться крюками или иметь приваренную поперечную арматуру по длине заделки. К величине R_b допускается вводить коэффициенты условий рабо­ты бетона, кроме .

В случае, когда анкеруемые стержни поставлены с запасом по площади сечения против требуемой расчетом по прочности с полным расчетным сопротивлением, вычисленную по формуле (11.7) длину анкеровки 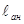допускается уменьшать, умножая на отношение необходимой по расчету и фактичес­кой площадей сечения арматуры.

Если по расчету вдоль анкеруемых стержней об­разуются трещины от растяжения бетона, то стерж­ни должны быть заделаны в сжатую зону бетона на длину 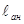, определяемую по формуле (11.7).

При невозможности выполнения указанных тре­бований должны быть приняты меры по анкеровке продольных стержней для обеспечения их работы с полным расчетным сопротивлением в рассматри­ваемом сечении (постановка косвенной арматуры, приварка к концам стержней анкерующих пластин или закладных деталей, отгиб анкерующих стерж­ней). При этом величина 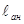должна быть не менее 10 d.

По п.5.15 для обеспечения анкеровки всех продоль­ных стержней арматуры, заводимых за грань опоры, на крайних свободных опорах изгибаемых элемен­тов должны выполняться следующие требования:

а) если соблюдаются условия 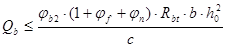, длина за­пуска растянутых стержней за внутреннюю грань свободной опоры должна составлять не менее 5 d;

б) если условия 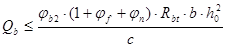не соблюдаются, длина запуска стержней за внутреннюю грань свободной опоры должна быть не менее 10 d.

По п.5.20 (а также по п.8.3.7 СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры») в балках шириной свыше 150 мм число про­дольных рабочих стержней, заводимых за грань опо­ры, должно быть не менее двух. В ребрах сборных панелей, настилов, часторебристых перекрытий и т. п. шириной 150 мм и менее допускается доведе­ние до опоры одного продольного рабочего стержня.

В плитах расстояния между стержнями, заводи­мыми за грань опоры, не должны превышать 400 мм, причем площадь сечения этих стержней на 1 м ширины плиты должна составлять не менее 1/3 площади сечения стержней в пролете, опреде­ленной расчетом по наибольшему изгибающему моменту (аналогично п. 8.3.8 7 СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры»).

По п.5.21 в изгибаемых элементах при высоте сече­ния свыше 700 мм у боковых граней должны ставится конструктивные продольные стержни с расстояниями между ними по высоте не более 400 мм, по ширине — половине ширины ребре элемента, но не более 200 мм.

Поперечная арматура в балочных и плитных конструкциях, устанавлива­ется:

— на приопорных участках, равных при равно­мерно распределенной нагрузке 1/4 пролета, а при сосредоточенных нагрузках — расстоянию от опоры до ближайшего груза, но не менее 1/4 проле­та, с шагом:

при высоте 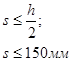, то же при

— на остальной части пролета при высоте сечения элемента h свыше 300 мм устанавливается попе­речная арматура с шагом не более 3/4 h и не бо­лее 500 мм.

Поперечная арматура, предусмотренная для восприятия поперечных сил, должна иметь на­дежную анкеровку по концам путем приварки или охвата продольной арматуры, обеспечивающую равнопрочность соединений и хомутов.

По СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры» по п.8.3.8 в балках до опоры следует доводить стрежни продольной рабочей арматуры с площадью сечения не менее ½ площади сечения стержней и не менее двух стержней.

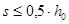
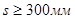
По п.8.3.11 в железобетонных элементах, в которых поперечная сила по расчету не может быть воспринята только бетоном, предусматривают установку арматуры с шагом и .

В балках и ребрах высотой 150 мм и более, а также в часторебристых плитах высотой 300 мм и более, на участках элемента, где поперечная сила по расчету воспринимается только бетоном, следует предусматривать установку поперечной арматуры с шагом 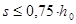и

Базовую длину анкеровки определяют по п. 8.3.21 по формулам 8.1-8.2.

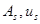
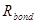
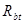
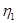
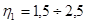
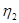
где – соответственно площадь поперечного сечения анкеруемого стержня арматуры и периметр его сечения, определяемые по номинальному диаметру стержня;

– расчетное сопротивление сцепления арматуры с бетоном, принимаемое равномерно распределенным по длине анкеровки и определяемое по формуле 8.2.

– расчетное сопротивление бетона осевому растяжению;

– коэффициент, учитывающий влияние вида поверхности арматуры ();

– коэффициент, учитывающий влияние размера диаметра арматуры.

Требуемую расчетную длину анкеровки арматуры с учетом конструктивного решения определяют по формуле 8.3

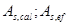
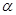
где – площади поперечного сечения арматуры соответственно требуемая по расчету и фактически установленная;

– коэффициент, учитывающий влияние на длину анкеровки напряженного состояния бетона и арматуры.

Допускается уменьшать длину анкеровки в зависимости от количества и диаметра арматуры, вида анкерующих устройств и величины поперечного обжатия бетона в зоне анкеровки, но не более чем на 30%.

Фактическую длину анкеровки принимают

ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ, АРМИРОВАННЫЕ ЖЕСТКОЙ АРМАТУРОЙ

Совместное деформирование жесткой арматуры и бетона сохраняется вплоть до разрушения элементов. В период разрушения несущая способность жесткой арматуры и бетона сжатой зоны используется полностью; при этом несущая способность элементов не зависит от первоначальных напряжений в арматуре, приобретенных ею в процессе возведения конструкций.

В элементах, армированных низкими профилями, для связи бетона сжатой зоны сечения с жесткой арматурой к последней приваривают специальные анкерные стержни или устанавливают хомуты. При отсутствии связи бетона сжатой зоны с жесткой арматурой разрушение элемента происходит от среза бетона сдвигающими силами по плоскости контакта с жесткой арматурой.

Рис. 11.20. Армирование элемента жесткой арматурой с низким профилем

1 – сжатая зона сечения;

2 – напряжения в бетоне сжатой зоны;

3 – напряжения растяжения в жесткой арматуре

В элементах, армированных высокими профилями (почти на всю высоту сечения), совместность деформирования обеспечивается и при отсутствии хомутов, т.к. сплошная металлическая стенка полностью воспринимает поперечную силу.

Рис. 11.21. Армирование элемента жесткой арматурой с высоким профилем

1 – сжатая зона сечения;

2 – напряжения в бетоне сжатой зоны;

3 – напряжения растяжения в жесткой арматуре;

4 – напряжения сжатия в сжатой арматуре

До бетонирования элементов жесткую арматуру рассчитывают по нормам проектирования стальных конструкций на воздействие нагрузок, возникающих в процессе возведения зданий (от бетона и опалубки, транспорта и т.д.)

Расчет сечений изгибаемых элементов с жесткой арматурой ведут по аналогии с расчетом изгибаемых элементов с гибкой арматурой, при этом учитывая сопротивление стального профиля.

Источник

Построение эпюр нормальных сил N

Правило знаков для N имеет физический смысл: нормальная сила является положительной, если вызывает растяжение бруса, отрицательной – если сжатие.

Пример 1 (рис. 1.3).

Если на стержень действуют силы, приложенные вдоль его оси, то он находится в условиях растяжения и остается только один внутренний фактор N.

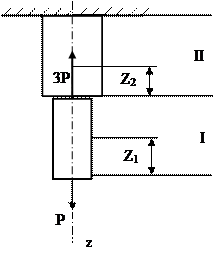Рис. 1.3 Стержень

Порядок построения эпюр:

1. Определяем реакции опор.

2. Разбиваем стержень на участки.

Участок – часть стержня между точками приложения сосредоточенных сил, включая опорные реакции.

3. Записываем аналитические выражения для внутренних силовых факторов.

4. Строим график (эпюру) (рис. 1.4).

Рис. 1.4 Построение эпюры нормальных сил

Эпюра – график, заштрихованный линиями, перпендикулярными оси.

Используя метод РОЗУ, отбрасывают ту часть, где больше нагрузки.

Внутренний фактор – равнодействующая внутренних сил.

Пример 2 (рис. 1.5).

Построить эпюру нормальных сил N.

q – интенсивность равномерно – распределенной нагрузки.

Опасное сечение в заделке, т.к. там самое большое значение N.

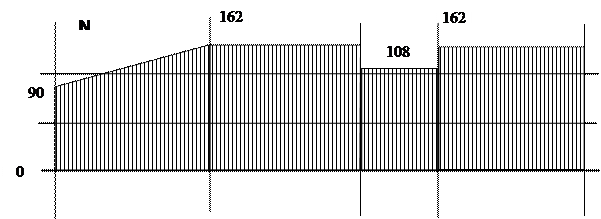Рис. 1.5 Построение эпюры нормальных сил

Построим эпюру нормальных сил

Построение эпюр крутящих моментов

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент, а прочие силовые факторы равны нулю. Для крутящего момента, независимо от формы сечения, принято следующее правило знаков.

Рис. 1.6 Правило знаков для крутящего момента

Если со стороны внешней нормали к сечению вращение осуществляется против часовой стрелки, то крутящий момент положительный (рис.1.6).

Правило знаков носит формальный характер (можно установить произвольно).

Стержень, в основном работающий на кручение, называется валом.

Рис.1.7 Схематичное изображение крутящего момента (против часовой стрелки).

Построить эпюру крутящих моментов (рис 1.9).

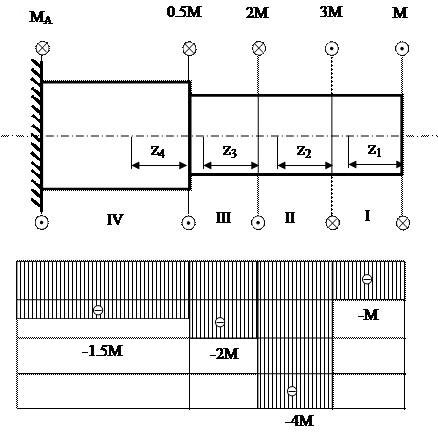Рис.1.9 Построение эпюры крутящих моментов

Пример на построение эпюры крутящих моментов (рис 1.10).

Рис. 1.10 Построение эпюры крутящих моментов

Построение эпюр поперечных сил Q и изгибающих моментов M для балок

Балка – стержень, в основном работающий на изгиб. При расчете балку принято заменять ее осью, все нагрузки приводятся к этой оси, а силовая плоскость будет совпадать с плоскостью чертежа.

Вал – стержень в основном работающий на кручение.

Виды опор:

Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).

Рис. 1.11 Шарнирно-подвижная опора

Шарнирно-неподвижная опора – опора, в которой могут возникать две составляющие реакции: вертикальная и горизонтальная (рис.1.12).

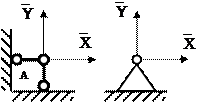Рис.1.12 Шарнирно-неподвижная опора

Заделка (жесткое защемление) – опора, в которой могут быть: вертикальная и горизонтальная реакции и опорный момент (рис.1.13).

Рис.1.13 Заделка

1.3.1 Правило знаков для Q

1.3.2 Правило знаков для М

Эпюру для М строят на сжатых волокнах.

Построить эпюры внутренних усилий Q и M для однопролетной балки (рис. 1.14).

Рис. 1.14 Расчетная схема

Вычислим реакции опор.

Освободим балку от связей и заменим их действие реакциями.

Составим уравнения равновесия:

Сумма моментов всех сил относительно точки А равна

Сумма моментов всех сил относительно точки В равна

Разделим балку на четыре участка. Применим метод сечений на каждом из участков и запишем выражения для внутренних усилий

Внутренние усилия на втором участке равны

На третьем участке

Внутренние усилия на четвертом участке равны

Строим эпюры для M и Q (рис 1.15). Для проверки правильности полученных эпюр могут быть использованы следствия из дифференциальных зависимостей между Q и M.

Рис. 1.15 Построение эпюр Q и M

Дифференциальные зависимости при изгибе

Пусть стержень закреплен произвольным образом и нагружен распределенной нагрузкой q = f(z), принятое направление q считать положительным (рис. 2.1).

Рис. 2.1 Стержень с распределенной нагрузкой

Выделим из стержня элемент длиной dz и в проведенных сечениях приложим моменты M и M + dM, а также поперечные силы Q и Q + dQ (рис. 2.2). В пределах малого отрезка dz нагрузку q можно считать равномерно распределенной.

Рис. 2.2 Элемент длиной dz стержня

Приравниваем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов относительно поперечной оси:

После упрощения получим:

Из полученных соотношений можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого стержня.

Правила проверки эпюр

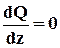
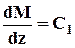
1. Если на участке отсутствует распределенная нагрузка, то есть q = 0, = > Q = const = C₁; => M = C₁ × z + D₁, то эпюра поперечных сил постоянна, а эпюра изгибающих моментов М изменяется по линейному закону (рис. 2.3).

Рис. 2.3 Эпюра поперечных сил и изгибающих моментов

2. Если в сечении приложена сосредоточенная сила, то на эпюре Q скачек на величину этой силы, от начала предыдущего, до начала следующего. А на эпюре М излом, направленный навстречу этой силе.

4.

Если в сечении приложен сосредоточенный момент М_i, то на эпюре Q нет никаких изменений, а на эпюре М скачек на величину этого момента (рис. 2.4).

Рис. 2.4 Эпюра поперечных сил и изгибающих моментов

5.

Если на участке приложена равномерно распределенная нагрузка q = const, то Q – наклонная прямая, а М – парабола, выпуклость которой направлена навстречу нагрузке (рис. 2.5).

Рис. 2.5 Эпюра поперечных сил и изгибающих моментов

6. Если на участке эпюра Q меняет знак и пересекает ось, то эпюра М имеет экстремум в точке пересечения Q с осью.

7. Если ветви эпюры Q сопрягаются без скачка на границах участка, то ветви эпюры М на границе этих же участков сопрягаются без изломов (рис. 2.6).

Рис. 2.6 Эпюра поперечных сил и изгибающих моментов

8. Если на участке стержня Q равна нулю, то 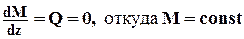(рис. 2.7)

Рис. 2.7 Эпюра поперечных сил и изгибающих моментов

3. Напряжения и деформации

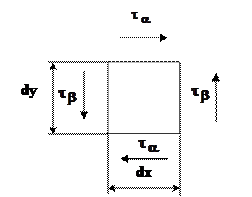
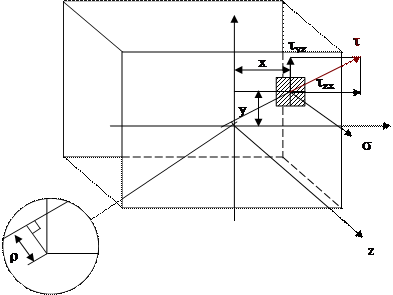
Введем оси координат Ox, Oy, Oz. Выделим элементарную площадку DF в плоскости поперечного сечения бруса (рис. 3.1). На нее действует произвольная сила, которая может быть разложена на составляющие DN (DNûëxOy) и DT (DTÎxOy).

z

Рис. 3.1 Поперечное сечение бруса

Введем понятие касательного и нормального напряжений:

нормальное напряжение

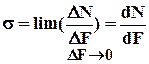
Нормальное напряжение – это предел отношения нормальной составляющей внутренних усилий DN, действующих на элементарную площадку DF при стремлении последней к нулю.

касательное напряжение

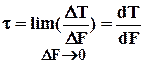
Касательное напряжение – это предел отношения тангенциальной составляющей внутренних усилий DT, действующих на элементарную площадку DF при стремлении последней к нулю.

Общий вид формул:

Закон парности касательных напряжений

«Вырежем» элементарную площадку dF бруса размером dx на dy (рис. 3.2).

Рис. 3.2 Площадка dF

На двух взаимно перпендикулярных площадках, имеющих общее ребро, касательные напряжения 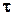равны по величине и направлены или оба к ребру или оба от ребра.

Интегральные зависимости между s и t и внутренними силовыми факторами

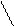
Рис. 3.3 Связь между напряжениями и внутренними усилиями

Деформации

Ни один из существующих в природе материалов не является абсолютно твердым; под действием внешних сил все тела в той или иной мере меняют свою форму(деформируются).

Изменение формы напряженного тела существенно влияет на распределение в нем внутренних сил, хотя само по себе это изменение формы является, как правило, незначительным и обнаруживается в большинстве случаев только при помощи чувствительных приборов.

Рассмотрим основные виды деформации, которые учитываются при решении задач в сопротивлении материалов.

Источник