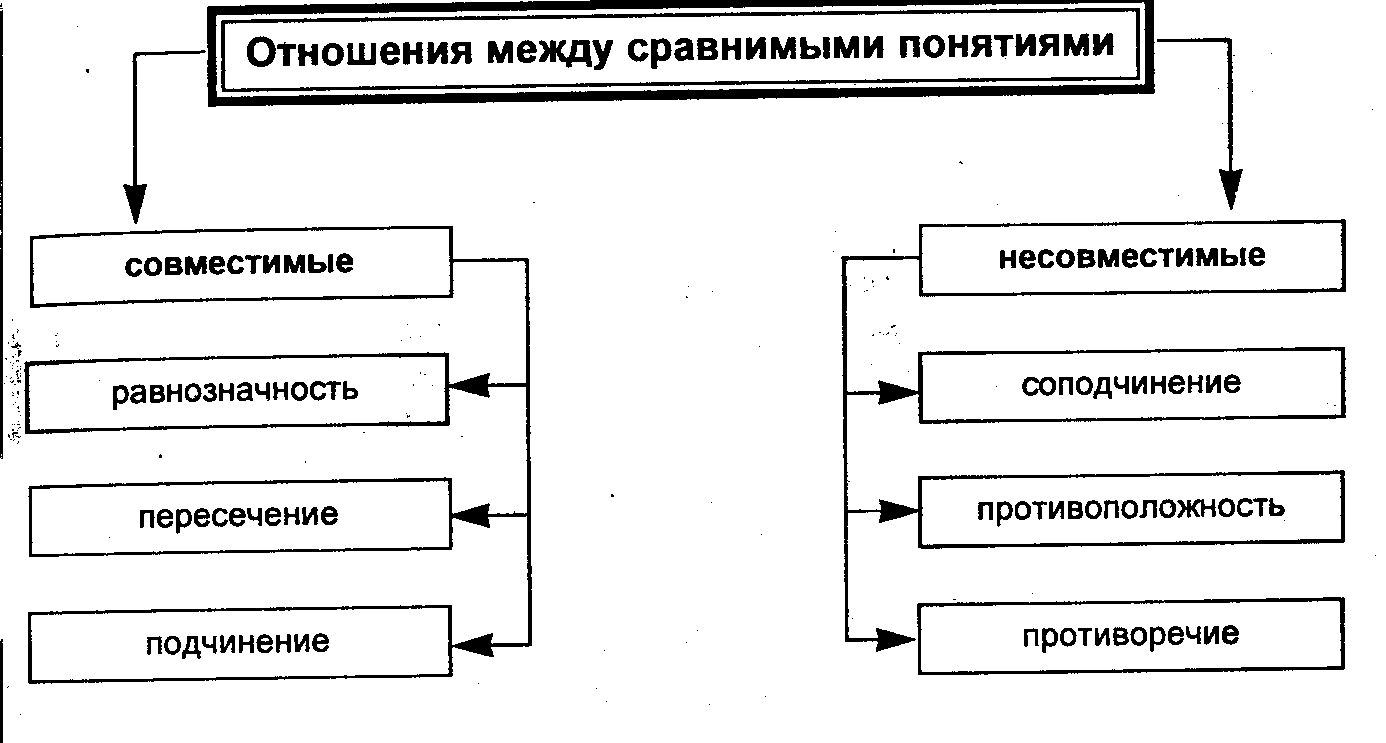
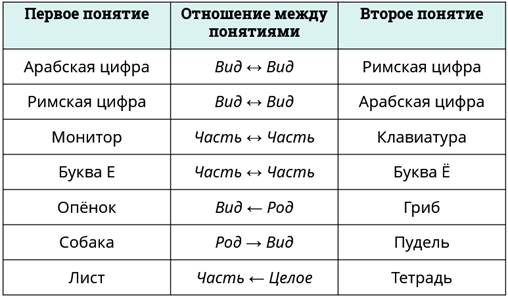
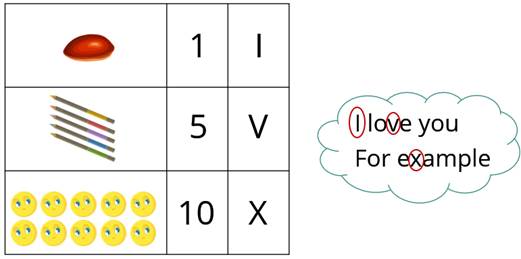
как удобно представлять отношения между понятиями

§ 5. Логические отношения между понятиями

§ 5. Логические отношения между понятиями

Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объема понятий, которые сравниваются.

Если понятия не имеют общих признаков, далеки друг от друга по свое­му содержанию, то они называются несравнимыми. Например, «симфониче­ская музыка» и «кассационная жалоба», «процессуальные акты предварительного расследования» и «общая тетрадь».

Сравнимыми называются понятия, отражающие некоторые общие суще­ственные признаки предмета или класса однородных предметов. Например, «юрист» и «адвокат», «взятка» и «кража».

В логических отношениях могут находиться только сравнимые понятия. В зависимости от того, как соотносятся их объемы, понятия делятся на две группы: совместимые и несовместимые.

Рассмотрим совместимые понятия.

В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (су­щественный признак) данного предмета или класса однородных предметов.

Необходимо отличать равнозначные понятия от равнозначных слов-синонимов. У равнозначных понятий одинаковый объем, но разное содержание. А слова-синонимы выражают понятия с одинаковым объемом и содержанием. Замена в любом осмысленном высказывании слов-си­нонимов друг с другом не влияет на смысл высказывания. Замена же слов, вы­ражающих равнозначные понятия, может привести к существенному искаже­нию смысла. Например, в высказывании «В 1980 году Москва была столицей игр XXII Олимпиады» нельзя заменить понятие «столица игр XXII Олимпиа­ды» равнозначным ему понятием «центр Московской области». Таким обра­зом, слова или словосочетания, выражающие равнозначные понятия, сами по себе не являются равнозначными.

В отношении пересечения находятся совместимые поня­тия, у которых объемы частично совпадают. Частично совпадает и содержание данных понятий.

В отношении подчинения находятся совместимые понятия, объем одно­го из которых полностью входит в объем другого, составляя его часть.

Объем первого понятия шире объема второго поня­тия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества.

Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом по отношению к понятию с меньшим объемом (подчиненному), а последнее по отношению к первому называется видовым, или видом. Родовидовые отноше­ния лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения.

Перейдем к рассмотрению несовместимых понятий.

При иллюстрации отношений между несовместимыми понятиями возни­кает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий.

В отношении соподчинения находятся два или более непересекающихся понятий, принадлежащих общему родо­вому понятию.

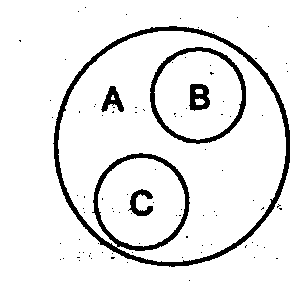
В отношении противоположности находятся понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-то признаки, а другое эти признаки отрицает и заменяет противоположными при­знаками.

В отношении противоречия находятся такие два поня­тия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.

Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями дает возможность пе­рейти к рассмотрению логических действий, или операций над понятиями.

Читайте также

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ При образовании понятий часто бывает важно не только указывать их вид, но и выяснять, в каком отношении находятся эти понятия к другим понятиям. Высказывания типа “это понятие близко такому-то понятию” только запутывают суть дела. Нужно

Логические отношения между простыми атрибутивными суждениями

Логические отношения между простыми атрибутивными суждениями Так же, как и понятия, суждения могут быть сравнимыми и несравнимыми. Мы можем рассмотреть только сравнимые суждения. Сравнимыми называются суждения с одинаковыми субъектами и предикатами и различающиеся

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ Рассматривая отношения между понятиями, следует прежде всего различать понятия сравнимые и несравнимые.Сравнимыми называются понятия, имеющие некоторые признаки, позволяющие эти понятия сравнивать. Например, «пресса» и «телевидение» —

§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ

§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ Суждения делятся на сравнимые и несравнимые.Несравнимыми являются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты

§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ

§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ При образовании понятий часто бывает важно не только указывать их вид, но и выяснять, в каком отношении находятся эти понятия к другим понятиям. Высказывания типа “это понятие близко такому-то понятию” только запутывают суть дела. Нужно

Глава III. Отношения между понятиями

Глава III. Отношения между понятиями Объективные отношения между самими предметами находят свое отражение в отношениях между понятиями. Все многообразие этих отношений можно классифицировать также на основе важнейших логических характеристик понятия: его содержания и

1. Отношения между понятиями по их содержанию

1. Отношения между понятиями по их содержанию Сравнимые понятия. По содержанию могут быть два основных вида отношений между понятиями — сравнимость и несравнимость. При этом сами понятия соответственно называются «сравнимыми» и «несравнимыми».Сравнимые — это понятия,

2. Отношения между понятиями по их объему

2. Отношения между понятиями по их объему Совместимые понятия. Сравнимые понятия могут по объему также иметь два основных вида отношений — совместимость и несовместимость. А сами соотносящиеся понятия называются «совместимыми» и «несовместимыми».Совместимые — это

3. Логические отношения между теориями

3. Логические отношения между теориями Если логические отношения существуют между понятиями и между суждениями, то вправе ли мы говорить о логических отношениях между теориями? Ведь это неизмеримо более сложные мыслительные конструкции! Да, вправе и именно потому, что

Глава III. Отношения между понятиями

Глава III. Отношения между понятиями 1. Отношения между понятиями по их содержанию Сравнимые и несравнимые понятия1. Определите, какие из названных ниже пар понятий сравнимые, какие — несравнимые: «металл» — «золото», «вода» — «камень», «космос» — «ключ», «душа»—«песня»,

1. Отношения между понятиями по их содержанию

1. Отношения между понятиями по их содержанию Сравнимые и несравнимые понятия1. Определите, какие из названных ниже пар понятий сравнимые, какие — несравнимые: «металл» — «золото», «вода» — «камень», «космос» — «ключ», «душа»—«песня», «правовой нигилизм» — «соната»,

2. Отношения между понятиями по их объему

2. Отношения между понятиями по их объему 1. Какие из указанных ниже пар понятий относятся к совместимым, а какие — к несовместимым: «снег» — «дождь», «время года» — «зима», «самолет» — «вертолет», «ложка» — «вилка», «мужчина» — «женщина», «рыба» — «муравей», «учитель»

§ 1. Возможные логические отношения между суждениями

§ 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения могут быть связаны и другими отношениями.

ЛЕКЦИЯ № 7 Отношения между понятиями

ЛЕКЦИЯ № 7 Отношения между понятиями 1. Общая характеристика отношений между понятиями Окружающий нас мир по своей природе — очень сложная система. Проявляется эта природа в том, что все предметы, которые мы только можем себе представить, всегда находятся во

Глава 4. Логические категории и отношения между понятиями

Глава 4. Логические категории и отношения между понятиями Начинается глава с перечисления десяти Аристотелевых категорий. Насколько я понял Георгия Ивановича, эти категории — это самые общие, корневые классы всех понятий. Вот, собственно, список:1. Субстанция

Источник

Урок по теме «Отношения между понятиями»

Цели: составить представление об отношениях понятий:

различать эти понятия.

1. Организационный момент.

2. Актуализация знаний.

3. Теоретический материал.

При сравнении реальных объектов мы сравниваем их размеры, цвет, форму и прочее. Отношения между реально существующими объектами описываются словами: больше – меньше; длиннее – короче; ближе – дальше; выше – ниже; брат – сестра и так далее.

Понятия тоже можно сравнивать между собой. Но, в отличие от объектов реальной действительности, понятия не имеют ни цвета, ни запаха, ни размера. Понятия – это наши представления, наши мысли об объектах. При сравнении понятий сравнивают их содержания и их объемы.

Рассмотрим два понятия – “квадрат” и “прямоугольник”.

Как видно из таблицы, содержания понятий отличаются одним признаком: у квадрата длины всех сторон равны, а у прямоугольника длины противоположных сторон попарно равны.

Объем понятия “прямоугольник” больше объема понятия “квадрат”, так как все квадраты – тоже прямоугольники.

Отношения между понятиями удобно представлять кругами (такое представление называется диаграммами Эйлера–Венна).

Рис.1

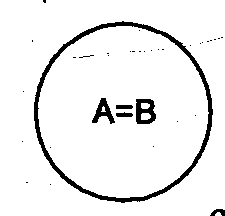
Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством.

Например, понятия “столица России” (А) и “город Москва” (В) – это тождественные понятия. Графическое представление отношения между ними будет выглядеть так:

Рис.2

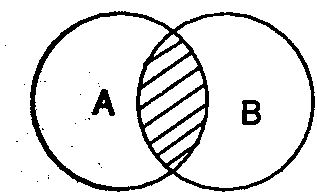
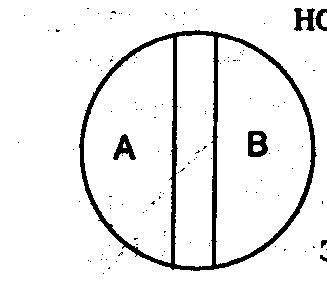
Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А – “электронное письмо”, В – “письмо на русском языке”. Тогда:

Рис. 3

В пересечение двух кругов попадают все электронные письма на русском языке.

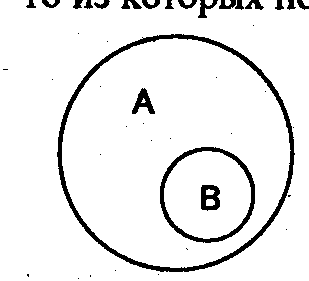
Подчинением называют отношение между понятиями, когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А – “клавиатура”, понятие В – “устройство ввода”. Тогда:

Рис. 4

Соподчинением называется отношение между несколькими понятиями, объемы которых не пересекаются, но которые принадлежат некоторому более общему (родовому) понятию. Это виды одного и того же рода. Пусть понятие А – “береста”, В – “папирус”, С – “глиняная дощечка”, П – “бумага”, Е – “магнитный диск”, Р – “носитель информации”. Здесь А, В, С, ^ и Е соподчинены Р:

Рис. 5

Слова, выражающие противоположные понятия, называются антонимами. Пусть понятие А – “компьютер с маленькой памятью”, понятие В – “компьютер с большой памятью”. Тогда:

Рис. 6

Объемы этих двух понятий разделены объемом некоторого третьего понятия, например, понятия “компьютер со средней памятью”.

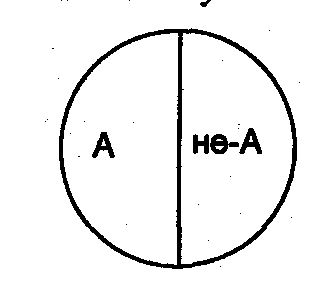
Пусть понятие А – “новый компьютер”. Тогда другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т. е. “неновый компьютер”). Круг, выражающий это отношение, делится на две части: третьего понятия между ними нет:

Рис. 7

4. Закрепление изученного материала. (Приложение.1)

Задание 1. Составьте пары сравнимых понятий и укажите их общий признак.

Понятия: веселье, весна, осень, монитор, клавиатура, грусть, стол, береза, автомобиль, диван, дерево, арбуз, гуляш, самолет.

Задание 2. Для каждого понятия запишите противоположное и противоречивое понятия.