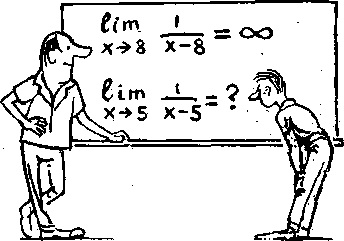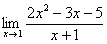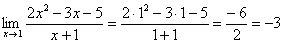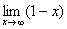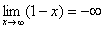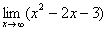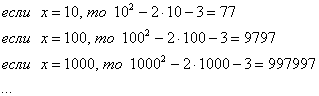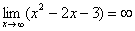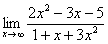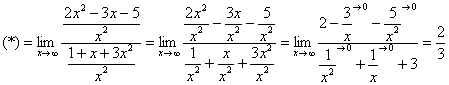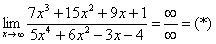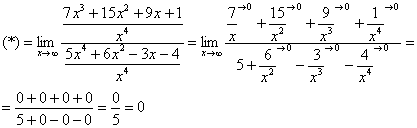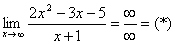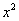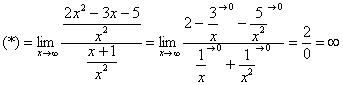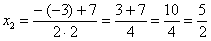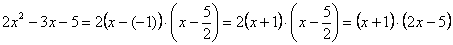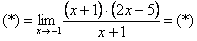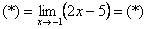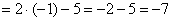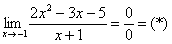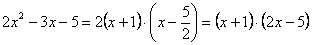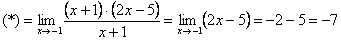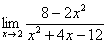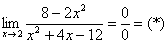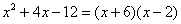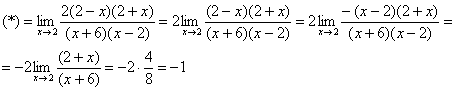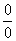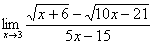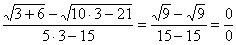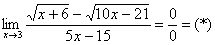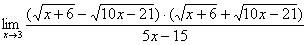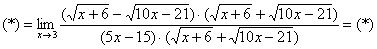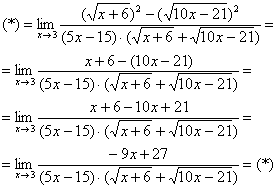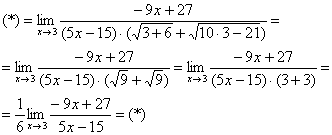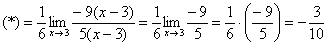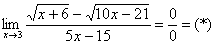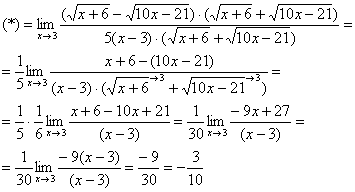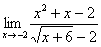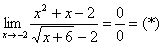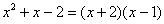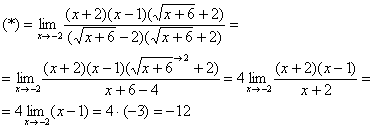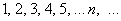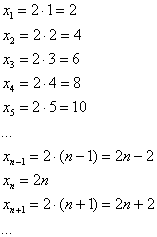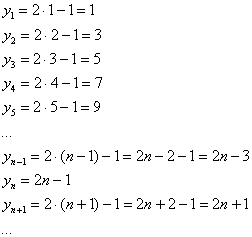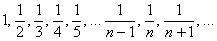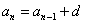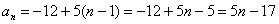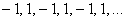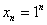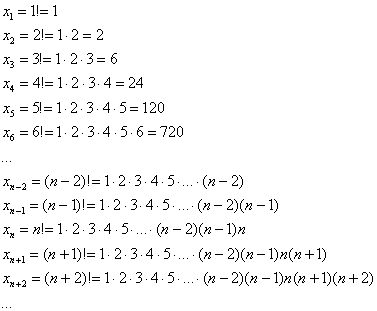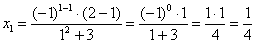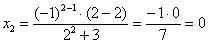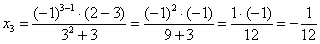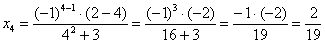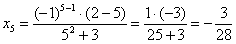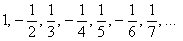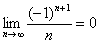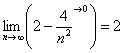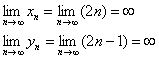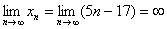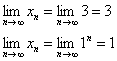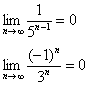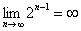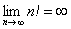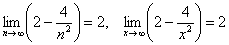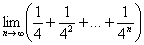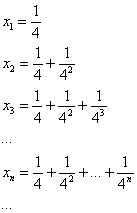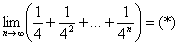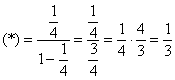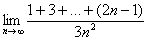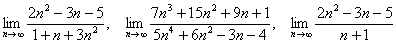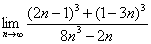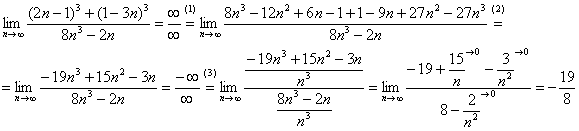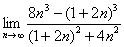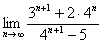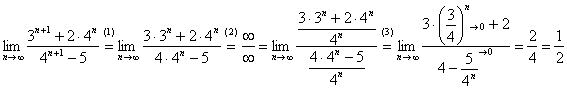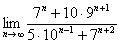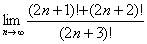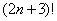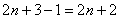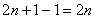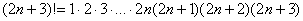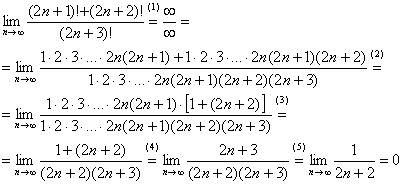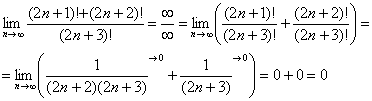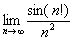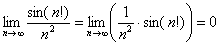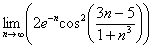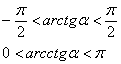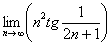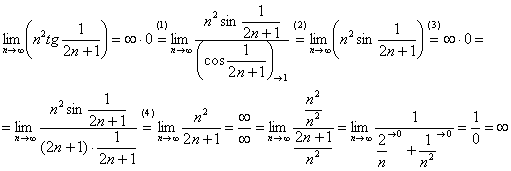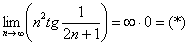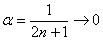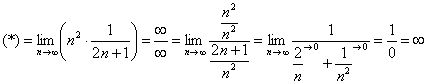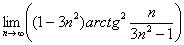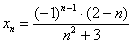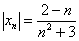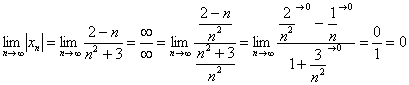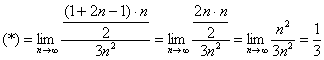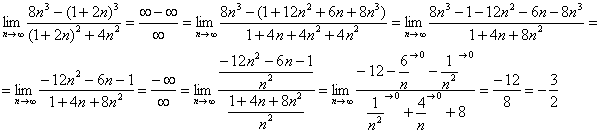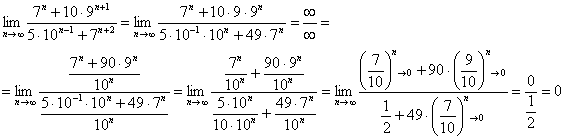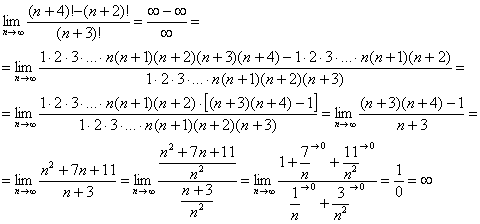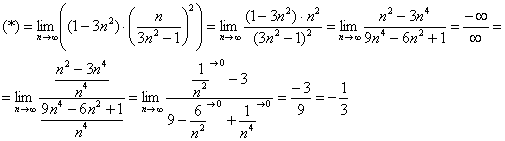Как вычислить предел
Как вычислить предел
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Внимание «чайникам» 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:
Продолжаем решать учитывая вышеприведенное преобразование:
Используя определение из примера 2 и подставляя в место х бесконечность получаем:
Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем.
Алгоритм вычисления лимитов
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Пределы функций. Примеры решений
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
Любой предел состоит из трех частей:
1) Всем известного значка предела 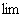
2) Записи под значком предела, в данном случае 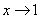
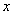
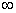
3) Функции под знаком предела, в данном случае 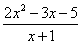
Сама запись 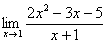
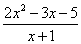
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 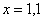
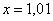
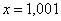
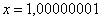
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 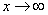
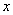
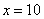
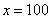
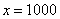
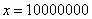
А что в это время происходит с функцией 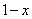
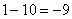
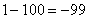
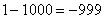
Итак: если 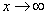
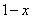
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 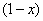
Еще один пример с бесконечностью:
Опять начинаем увеличивать 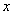
Вывод: при 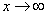
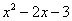
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
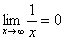
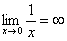
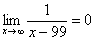
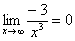
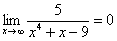
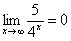
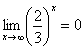
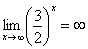
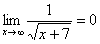
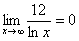
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 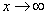
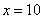
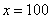
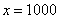
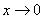
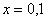
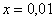
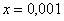
! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: 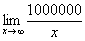
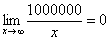
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как 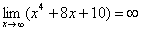
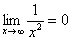
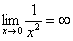
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!
На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:
Пределы с неопределенностью вида 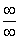
Сейчас мы рассмотрим группу пределов, когда 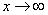
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 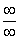
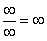
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 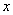
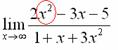
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 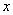
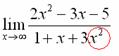
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 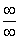
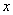
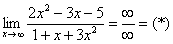
Разделим числитель и знаменатель на 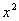
Вот оно как, ответ 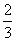
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 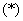
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: 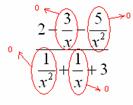
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Найти предел 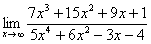
Снова в числителе и знаменателе находим 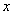
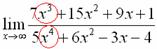
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 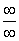
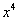
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Найти предел 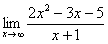
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( 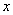
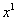
Для раскрытия неопределенности 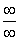
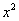
Разделим числитель и знаменатель на
Под записью 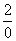
Таким образом, при раскрытии неопределенности вида 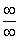
Пределы с неопределенностью вида 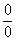
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 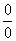
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: 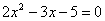
Сначала находим дискриминант: 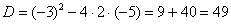
И квадратный корень из него: 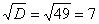
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни: 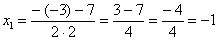
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель 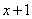
Очевидно, что можно сократить на 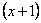
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители. 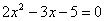
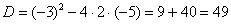
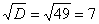
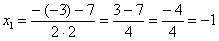
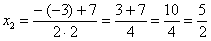
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: 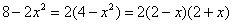
Знаменатель: 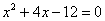
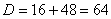
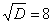
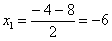
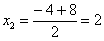
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида 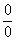
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 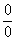
Вспоминаем нашу нетленную формулу разности квадратов: 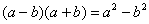
И смотрим на наш предел: 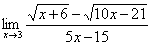
Что можно сказать? 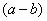
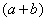
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 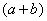
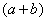
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу 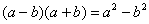
Неопределенность 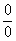
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители: 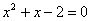
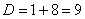
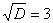
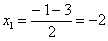
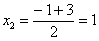
Умножим числитель и знаменатель на сопряженное выражение
Спасибо за внимание.
Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. После освоения двух базовых уроков, рекомендую изучить статью Методы решения пределов, материалы которой позволят выйти на «твёрдую четвёрку»!
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Пределы в математике для чайников: объяснение, теория, примеры решений
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Числовая последовательность.
Как найти предел последовательности?
На данном уроке мы узнаем много интересного из жизни участников большого сообщества под названием Вконтакте числовые последовательности. Рассматриваемая тема относится не только к курсу математического анализа, но и затрагивает основы дискретной математики. Кроме того, материал потребуется для освоения других разделов вышки, в частности, в ходе изучения числовых рядов и функциональных рядов. Можно банально сказать, что это важно, можно ободряюще сказать, что это просто, можно сказать ещё много дежурных фраз, однако сегодня первая, необыкновенно ленивая учебная неделя, поэтому меня жутко ломает сочинять первый абзац =) Уже в сердцАх сохранил файл и собрался спать, как вдруг… голову озарила идея чистосердечного признания, которое невероятно облегчило душу и подтолкнуло к дальнейшему стуку пальцами по клавиатуре.
Отвлечёмся от летних воспоминаний, и заглянем в этот увлекательный и позитивный мир новой социальной сети:
Понятие числовой последовательности
Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.
Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:
С числами всё аналогично. Пусть каждому натуральному значению 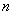
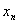
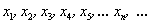
Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.
При этом:
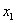
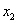
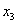
…
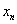
…
На практике последовательность обычно задаётся формулой общего члена, например:
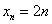
Таким образом, запись 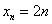
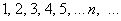
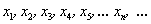
Последовательность положительных нечётных чисел 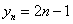
Ещё одна распространённая последовательность 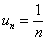
Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.
На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть 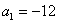
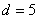
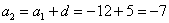
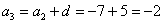
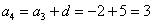
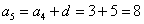
…
И, очевидно, энный член задаётся рекуррентной формулой
Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.
Полученная формула малопригодна на практике – чтобы добраться, скажем, до 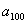
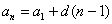
Подставьте в формулу 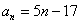
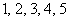
Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой 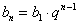
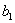
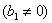
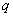
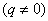
прогрессия 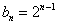
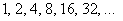
прогрессия 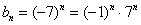
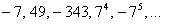
прогрессия 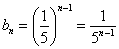
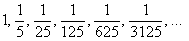
прогрессия 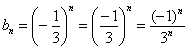
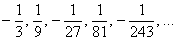
Надеюсь, все знают, что –1 в нечётной степени равно –1, а в чётной – единице.
Прогрессию называют бесконечно убывающей, если 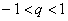
Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:
Последовательность 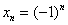
Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.
А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например, 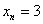
Факториал: 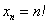
Всего лишь свёрнутая запись произведения:
Отнюдь не графомания, пригодится для задач 😉 Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)
Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:
Разберёмся с последовательностью 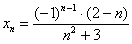
Сначала подставим в энный член значение 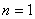
Далее подставим в общий член 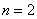
Потом подставим следующий номер 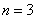
Четвёрку:
Чего уж, теперь и отличную отметку не зазорно заработать:
и так далее… пока разогреется самый последний чайник!
Понятие предела последовательности. Простейшие примеры
Для лучшего осмысления нижеследующей информации желательно ПОНИМАТЬ, что такое предел функции. Конечно, в стандартном курсе математического анализа сначала рассматривают предел последовательности и только потом предел функции, но дело в том, что о самой сущности предела я уже подробно рассказывал. Более того, в теории числовая последовательность считается частным случаем функции, и людям, которые знакомы с пределом функции, будет заметно веселее.
Впрочем, дальше могут читать все-все-все, однако если у вас возникнет непонимание или недопонимание чего-либо, то, пожалуйста, начните с пределов функций.
Пригласим на танец незамысловатую подругу 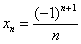
Что происходит, когда «эн» увеличивается до бесконечности? Очевидно, что члены последовательности будут бесконечно близко приближаться к нулю. Это и есть предел данной последовательности, который записывается следующим образом:
Если предел последовательности равен нулю, то её называют бесконечно малой.
В теории математического анализа даётся строгое определение предела последовательности через так называемую эпсилон-окрестность. Этому определению будет посвящёна следующая статья, а пока что разберём его смысл:
Изобразим на числовой прямой члены последовательности 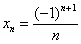
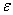
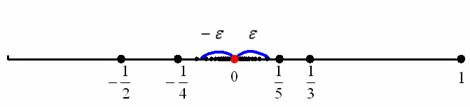
Теперь зажмите синюю окрестность рёбрами ладоней и начинайте её уменьшать, стягивая к пределу (красной точке). Число 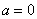
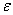
Последовательность 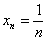
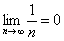
Естественно, предел может быть равен и любому другому конечному числу, элементарный пример:
Здесь дробь стремится к нулю, и соответственно, предел равен «двойке».
Если у последовательности 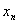
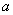
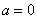
Последовательности 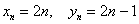
Арифметическая прогрессия с первым членом 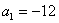
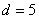
К слову, расходится и любая арифметическая прогрессия, за исключением случая с нулевым шагом – когда к конкретному числу 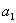
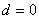
У последовательностей 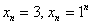
Любая бесконечно убывающая геометрическая прогрессия, как ясно уже из названия, бесконечно малА:
Если знаменатель геометрической прогрессии 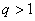
Если же 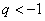
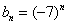
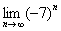
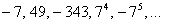
После небольшого разоблачения 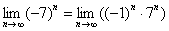
Действительно, для последовательности 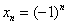
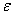
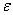
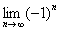
Факториал 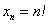
Причём, растёт он как на дрожжах, так, 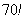
С контрольным выстрелом всё чуть сложнее, и мы как раз подошли к практической части лекции, в которой разберём боевые примеры:
Как найти предел последовательности?
А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:
В пределе последовательности «динамическая» переменная «эн» может стремиться только к «плюс бесконечности» – в сторону увеличения натуральных номеров 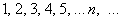
В пределе функции «икс» может быть направлен куда угодно – к «плюс/минус бесконечности» либо к произвольному действительному числу.
Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.
По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, такие как факториалы, «мигалки», прогрессии и т.п. И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.
Начнём с прогрессий:
Найти предел последовательности
Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:
Так как 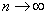
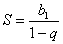
Используем формулу суммы бесконечно убывающей геометрической прогрессии: 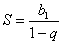
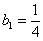
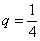
Главное, совладать с четырёхэтажностью дроби:
Написать первые четыре члена последовательности и найти её предел
Это пример для самостоятельного решения. Для устранения неопределённости 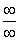
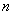
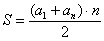
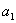
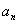
Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость 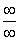
И многие примеры решаются точно так же, как пределы функций!
Как вычислить эти пределы? Смотрите Примеры № 1-3 урока Пределы. Примеры решений.
А может быть что-нибудь посложнее наподобие 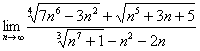
С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.
Также в пределах последовательностей достаточно распространена неопределённость 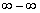
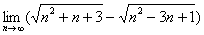
Чтобы разобраться с пределом 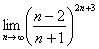
Следующие четыре примера (№ 3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:
Найти предел последовательности
Решение: сначала полное решение, потом пошаговые комментарии:
(1) В числителе дважды используем формулу 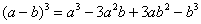
(2) Приводим подобные слагаемые в числителе.
(3) Для устранения неопределённости делим числитель и знаменатель на 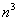
Как видите, ничего сложного.
Найти предел последовательности
Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.
В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:
Найти предел последовательности
Решение оформим по той же схеме:
(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».
(2) Смотрим, какие показательные последовательности есть в пределе: 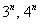
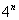
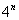
(3) В числителе и знаменателе проводим почленное деление. Поскольку 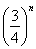
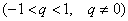
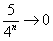
Найти предел последовательности
Это пример для самостоятельного решения.
Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:
Найти предел последовательности
Решение: чтобы избавиться от «вечного соперника» 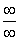
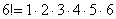
Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.
Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал». Давайте разделаемся с самым злостным флудером нашего чата:
Очевидно, что последним множителем в произведении будет 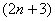
Как получить предыдущий множитель? Вычесть единицу:
Как достать прадедушку? Ещё раз вычесть единицу: 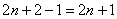
Ну и ещё на один шаг продвинемся вглубь:
Таким образом, наше чудовище распишется следующим образом:
С факториалами числителя всё проще, так, мелкие хулиганы.
Оформляем решение:
(1) Расписываем факториалы
(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение 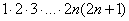
(3) Сокращаем числитель и знаменатель на 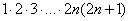
(4) Упрощаем числитель
(5) Сокращаем числитель и знаменатель на 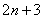
Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:
Но способ с разложением всё-таки более основателен и надёжен.
Найти предел последовательности
Это пример для самостоятельного решения.
Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150 прорешанных примеров можно найти здесь >>> (задачи № 2-6).
Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.
Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.
Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.
Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.
Найти предел последовательности
Решение: последовательность 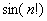
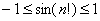
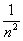
Просто и со вкусом. Да-да, так и оформляем.
А почему бы и нет?
Найти предел последовательности
Это пример для самостоятельного решения.
Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:
Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!
Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:
Найти предел последовательности
Решение: неопределённость 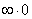
(1) Используем формулу 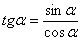
(2) Избавляемся от косинуса, указывая, что он стремится к единице.
(3) Неопределённость 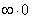
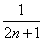
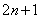
(4) Используем первый замечательный предел 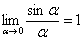
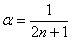
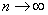
Прокатывает и 2-й метод решения – через замечательные эквивалентности:
Заменим бесконечно малую последовательность эквивалентной:
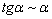
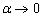
В данном случае
Найти предел последовательности
Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.
Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.
В заключение урока рассмотрим ещё один важный вопрос:
Как найти предел знакочередующейся последовательности?
Такая последовательность уже неоднократно встречалась в статье, например, первая скрипка теоретического параграфа 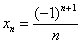
Действительно, как аналитически найти предел знакочередующейся последовательности, если знак то «плюс», то «минус»?
И я, наконец-то, заряжаю в свой револьвер тот самый волшебный патрон:
Найти предел последовательности
Решение: на первом шаге следует найти предел последовательности 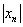
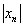
Теперь как ни в чём не бывало, вымучиваем наш обычный предел:
Получено конечное число. Очевидно, что знакочередование не поменяет сути – члены последовательности будут «прыгать» вокруг своего предела, бесконечно близко приближаясь к нему. Собственно, это проиллюстрировано на единственном рисунке данного урока.
Ситуация принципиально такая же, как, например, у более простых последовательностей 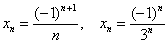
Ответ: так как последовательность является знакочередующейся и 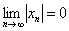
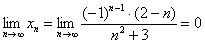
Если в ходе исследования знакочередующейся последовательности 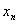
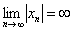
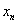
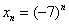
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Успехов в учёбе!
Решения и ответы:
Пример 2: Решение: 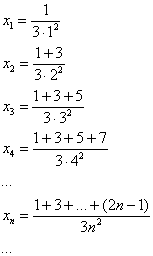
Найдём предел последовательности: 
Используем формулу суммы 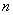
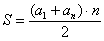
В данном случае 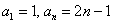
Пример 4: Решение:
Пример 6: Решение:
Пример 8: Решение:
Пример 10: Решение: последовательность 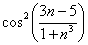
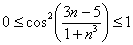
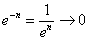
Пример 12: Решение: 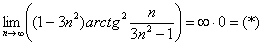
Заменим бесконечно малую эквивалентной: 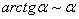
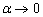
В данном примере 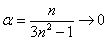
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение пределов.
Этот математический калькулятор онлайн поможет вам если нужно вычислить предел функции. Программа решения пределов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс вычисления предела.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Предел функции при \( x \to x_0 \)
Пусть функция \( f(x) \) определена на некотором множестве \(X\) и пусть точка \( x_0 \in X \) или \( x_0 \notin X \)
Определение. Число \(A\) называется пределом функции \(f(x)\) в точке \( x = x_0 \) (или при \( x \to x_0 \) ), если для любой сходящейся к \(x_0\) последовательности (1) значений аргумента \(x\), отличных от \(x_0\) соответствующая последовательность (2) значений функции сходится к числу \(A\).
Функция \(f(x)\) может иметь в точке \(x_0\) только один предел. Это следует из того, что последовательность \( \left\ < f(x_n) \right\>\) имеет только один предел.
Существует другое определение предела функции.
Предел функции при \( x \to x_ <0->\) и при \( x \to x_ <0+>\)
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение Число \(A\) называется правым (левым) пределом функции \(f(x)\) в точке \(x_0\), если для любой сходящейся к \(x_0\) последовательности (1), элементы \(x_n\) которой больше (меньше) \(x_0\), соответствующая последовательность (2) сходится к \(A\).
Кроме рассмотренных понятий предела функции при \( x \to x_0 \) и односторонних пределов существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение. Число \(A\) называется пределом функции \(f(x)\) при \( x \to \infty \), если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к \(A\).
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах последовательностей на функции. Покажем это на примере двух теорем.
Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида \( \frac<0> <0>\) и \( \frac<\infty> <\infty>\).
Предел функции: примеры решений
Обновлено: 24 Октября 2021
Рассмотрим понятие и определение предела, разберем основные решения пределов.
Разбор записи предела на математическом языке
Любой предел состоит из трех частей:
Данная запись читается так: «предел функции \(\lim_
Понятие предела, в отличие от большинства известных математических понятий, динамическое, то есть нет какого-то статичного, неменяющегося числа или тождества в качестве его определения. Построим последовательность:
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»? Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность:
Все данные значения x и разница между ними настолько малы и близки к одной точке (в данном случае к единице), что можно сказать, что «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают. Это и означает «икс стремится к единице».
Предел последовательности: определение и свойства
Предел последовательности, как и предел функции, является одним из основных понятий математического анализа. По сути, каждое вещественное число может быть представлено в виде последовательности максимально приближенных к нему чисел.
Вещественные (действительные) числа обозначаются как ε (эпсилон) и принадлежат множеству R, которое включает в себя все натуральные, целые, рациональные и иррациональные числа.
Теперь обратимся к определению предела последовательности и разберем, что же оно означает.
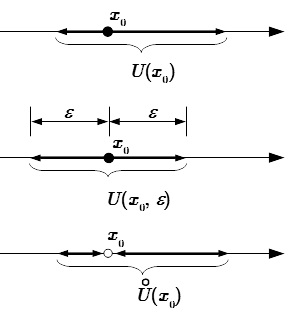
Для лучшего восприятия понятия «окрестность» рассмотрим следующее изображение:
Окрестностью в данном случае являются интервалы слева и справа от x0, причем окрестность может быть проколотой (третий случай), то есть сама точка x0 не входит в заданный интервал.
На математическом языке данное определение записывается следующим образом:
Свойства
1. Постоянный множитель c можно выносить за знак предела. На математическом языке данное утверждение выглядит так:
\(\lim_
где \(a_n\) — бесконечно малая величина. Очевидно, что:
где \(\alpha_n\) и \(\beta_n\) — некоторые бесконечно малые величины.
Тогда \(x_n\pm y_n=(A\pm B)+(\alpha_n\pm\beta_n)\)
Учитывая, что \((\alpha_n\pm\beta_n)\) — бесконечно малая величина, получаем:
\(\lim_<>(x_n\pm y_n)=(A\pm B)=\lim_<>(x_n)\pm\lim_<>(y_n) \) Аналогично:
\(x_n\times y_n=(A\pm\alpha_n)(B\pm\beta_n)=AB+(B\alpha_n+A\beta_n+\alpha_n\beta_n)\)
Осталось распознать в выражении \( (B\alpha_n+A\beta_n+\alpha_n\beta_n)\) бесконечно малую величину, что влечет за собой:
\(\lim_<>(x_n\times y_n)=AB=\lim_<>x_n\times\lim_<>y_n\\\\ \)
Далее покажем, что отношение \(\frac
Что и требовалось доказать.
Определенного доказательства данного свойства нет, однако интуитивно мы можем провести следующие умозаключения.
Пусть \(\underset<><\lim\;>y_n=A,\) тогда:
\(y_n=A+\alpha_n\)
где \( \alpha_n\) – некоторая бесконечно малая величина.
Что и требовалось доказать.
Предел функции
Обратимся сразу к определению.
Постоянное число А называется пределом функции f(x) при x→a, если, задав некоторое произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 \(\lim_
Для того, чтобы функция являлась непрерывной, обязательно должны выполнятся 3 условия:
Существуют и другие определения, которые, как и в случае с определением пределов по Коши и по Гейне, различаются по формулировке для наиболее удобного использования.
Если функция y=f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.
Также можно дать определение непрерывности справа или слева от точки.
Функция f(x) называется непрерывной справа/слева в точке x0, если она определена на некоторой правосторонней/левосторонней окрестности \(U(x_0+0)/U(x_0-0)\) этой точки, и если правый/левый предел в точке x0 равен значению функции в x0.
Вычисление пределов
Рассмотрим примеры вычисления пределов.
Простейшие пределы
Для начала обратимся к простейшему пределу, который был рассмотрен в самом начале: \(\lim_
В данном случае можно попробовать просто подставить единицу (так как предел стремится к единице) в выражение. Тогда:
Да, это работает только с простейшими пределами, которые, на самом деле, на практике встречаются не редко, так что попробовать просто подставить икс в выражение — одно из возможных решений.
Теперь попробуем сделать то же самое с пределом, который стремится к бесконечности.
Икс стремится к бесконечности \((x\rightarrow\infty)\) означает, что икс неограниченно возрастает (например, х=10, х=100, х=1000, х=10000 и так далее).
Рассмотрим предел \(\lim_
Даже если числитель функции в пределе, стремящимся к бесконечности, кажется очень большим — миллион, миллиард и т. п., весь предел все равно будет равен нулю, так как знаменатель, зависящий от бесконечности, в какой-то момент начнет принимать значения, гораздо большие, чем числитель. То есть:
Итак, когда мы видим простейший предел, сначала нужно попробовать подставить в функцию «х».
Выражения для самостоятельного решения:
Пределы с неопределенностью вида \(\frac\infty\infty\)
Неопределенность вида \(\frac\infty\infty\) появляется, когда мы пытаемся подставить «х» в предел стремящийся к бесконечности и имеющий дробную функцию:
Для начала находим и в числителе, и в знаменателе старшую степень икса, а затем выбираем наибольшую из них. В данном случае старшие степени числителя и знаменателя равны, однако это частный случай.
Теперь мы должны и числитель, и знаменатель разделить на х в старшей степени:
Затем анализируем дроби с иксом, мысленно подставляя вместо х бесконечность. Получается, что все эти дроби стремятся к нулю, соответственно, их можно принять за ноль. Значит:
Однако, ответом при решении предела, стремящегося к бесконечности, может быть как любое число — в том числе и ноль, — так и сама бесконечность.
Рассмотрим еще 2 примера, чтобы в этом убедиться.
Поделив числитель и знаменатель на \(x^4\) и подставив бесконечность в получившиеся дроби (для закрепления материала лучше высчитать это самостоятельно), получаем:
Пределы с неопределенностью вида \(\frac00\)
Сразу же возникает логичный вопрос: почему мы делим на ноль, если каждый школьник знает, что на ноль делить нельзя? Если обратиться к определению предела, все встанет на свои места: дело в том, что мы работаем не с самим нулем, а с бесконечно малыми числами и функциями, однако для удобства записываем «0».
Рассмотрим конкретные примеры и научимся решать подобные пределы.
Теперь запомним правило:
Почти всегда для этого необходимо решить квадратное уравнение и/или использовать ФСУ (формулы сокращенного умножения).
В знаменателе мы имеем x+1, это уже простейшая функция, так что знаменатель мы не трогаем.
Применяя стандартные операции для решения квадратного уравнения, раскладываем числитель и получаем (x+1)(5x-7).
Два важных момента, на которые стоит обратить внимание при вычислении дискриминанта:
Очевидно, что (х+1) в числителе и знаменателе можно сократить.
Очень важно при разложении на множители замечать формулы сокращенного умножения! Они могут быть видны не сразу, а после проведения одного или нескольких шагов, например, вынесения числа за скобку.
Чтобы облегчить процесс решения, всегда сразу выносите число за скобку, если это условие это позволяет. Кроме того, часто целесообразно выносить такие числа и за знаки предела, так как они не будут мешаться во время вычислений. Однако нужно быть крайне внимательным, чтобы не потерять в какой-то момент число или знак.
Теперь, для того, чтобы упростить выражение, нужно избавиться от корней. Вообще, в математике стараются избавляться от иррациональности в любом случае, когда это возможно, — так гораздо проще жить.
Что же это за метод? А основан он на всей известной формуле разности квадратов:
Теперь, учитывая формулу в числителе дроби, проводим ряд преобразований и получаем:
Да, избавившись от иррациональности в числителе, мы обрели ее в знаменателе, однако оперировать суммой корней, которую мы получили, гораздо легче. И, вообще, можно сразу подставить в корни тройку и вынести полученное число за знак предела, как упоминалось об это ранее.
А теперь просто раскладываем дробь на множители и получаем конечный ответ:
Примеры для самостоятельного решения:
Мы рассмотрели основное понятие пределов функции и последовательности и разобрали классические варианты решения пределов.
Если же быстро разобраться в этой сложной теме не получается, а сдача важной работы не за горами, вы всегда можете обратиться к авторам ФениксХелп, которые помогут с решением.