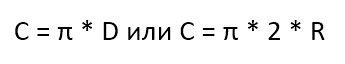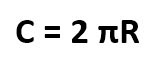Как высчитать длину окружности зная диаметр

Как вычислить длину окружности зная диаметр

Не знаете, как вычислить длину окружности, зная диаметр, или желаете проверить правильность решенной задачи? Определить этот параметр сможет этот онлайн калькулятор.

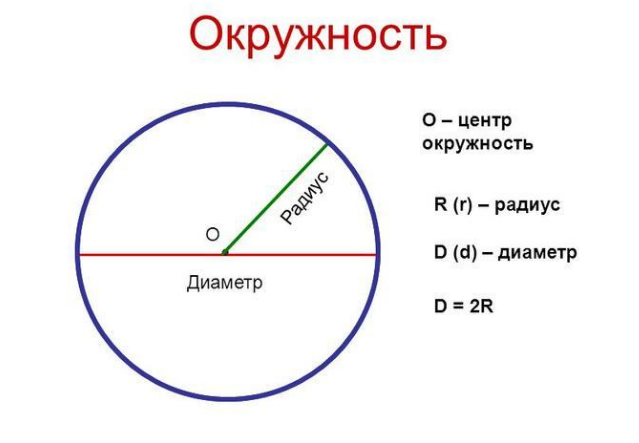
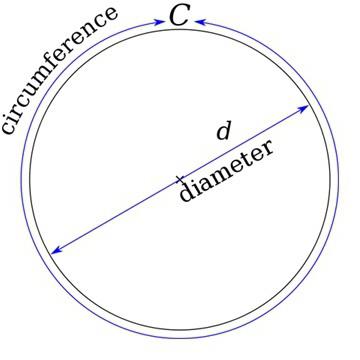
Круг – это плоская фигура из раздела геометрии. Каждая из ее точек располагается строго на одном расстоянии от центра круга. Это расстояние от центра до одной из точек называется радиусом, а отрезок, который соединяет две точки и включает в себя центр окружности – диаметром.

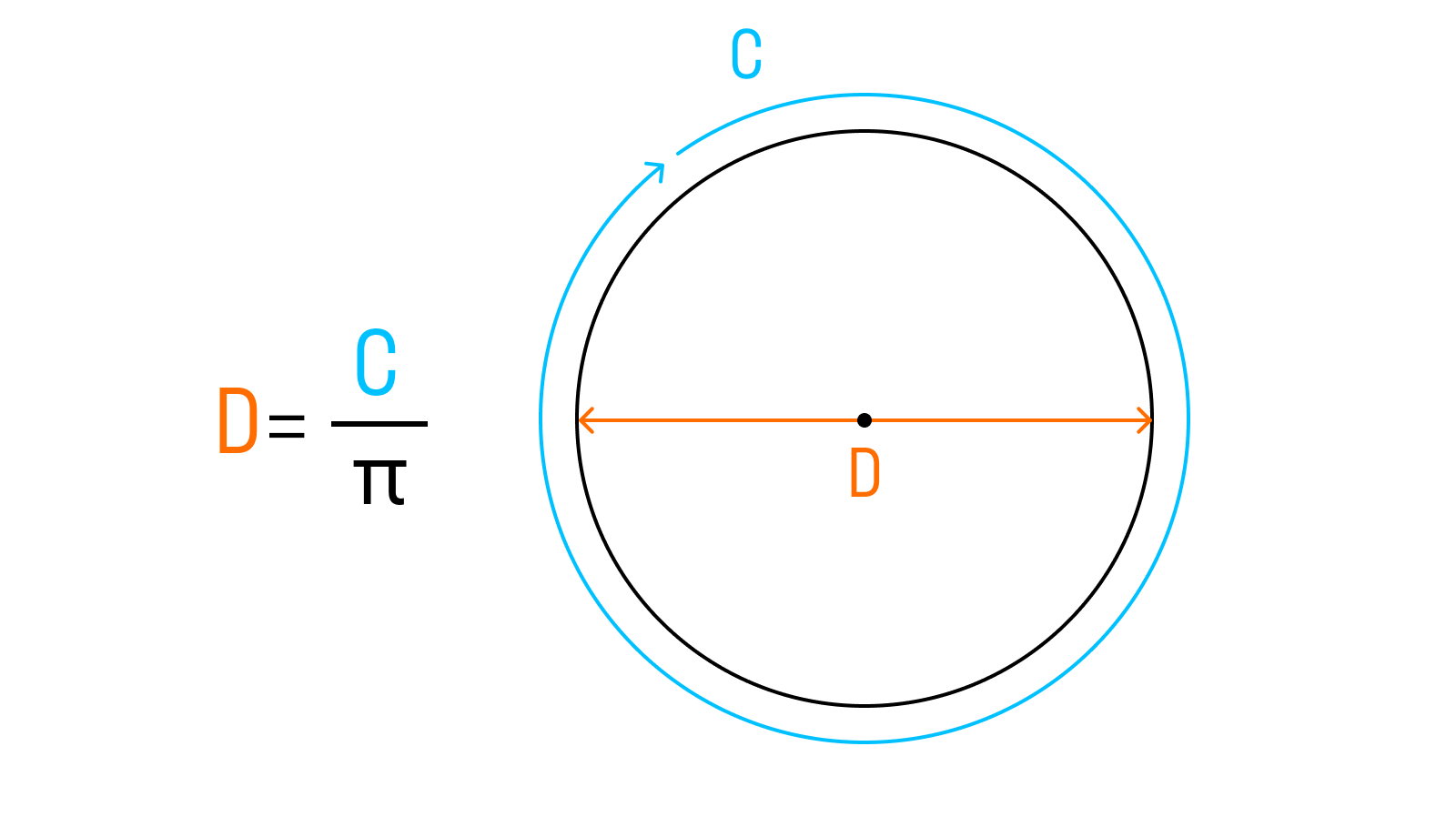
Формула, позволяющая рассчитать его окружность, такова: С = πd, где: π – число «пи», или 3,14, а d – диаметр окружности. Остается только ввести цифы, и задача решена!

Если диаметр вам неизвестен, то можно найти геометрическую величину через радиус – r: С = 2πr

Все формулы уже встроены встроены в онлайн-калькулятор. Чтобы воспользоваться ими занесите значения в соответствующие окошки и получите подробное решение своего примера под калькулятором.

Расчет длины окружности по радиусу на калькуляторе может понадобиться по многим причинам:

Не тратьте лишне время на расчеты и будьте уверены в правильности расчетов параметра!

Источник

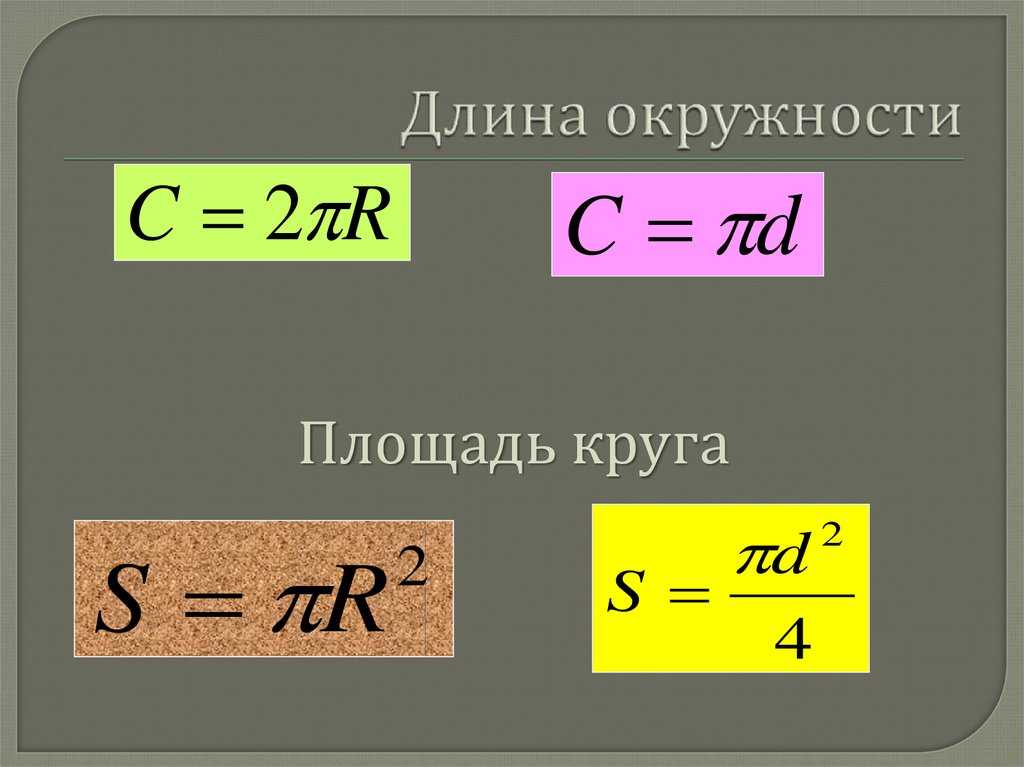
Длина окружности

6 класс, 9 класс, ЕГЭ/ОГЭ

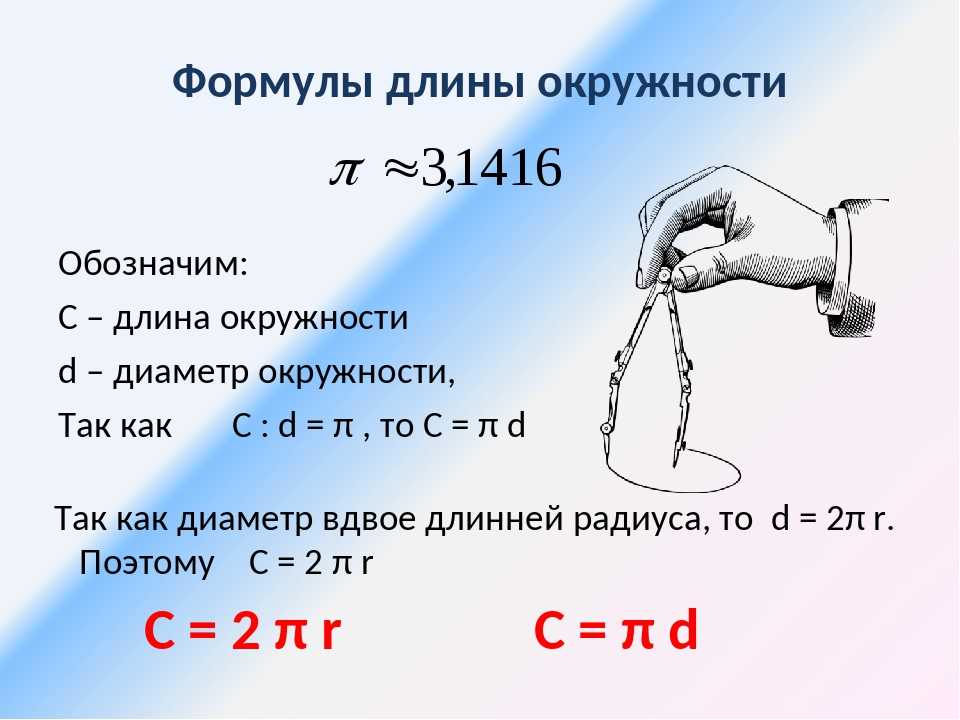
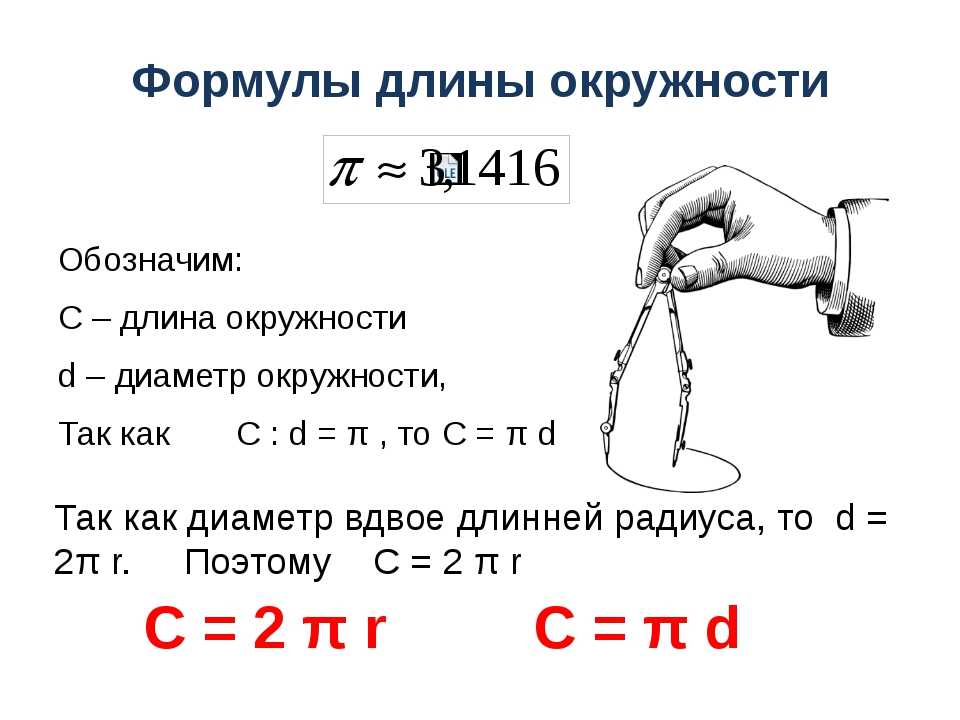
Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

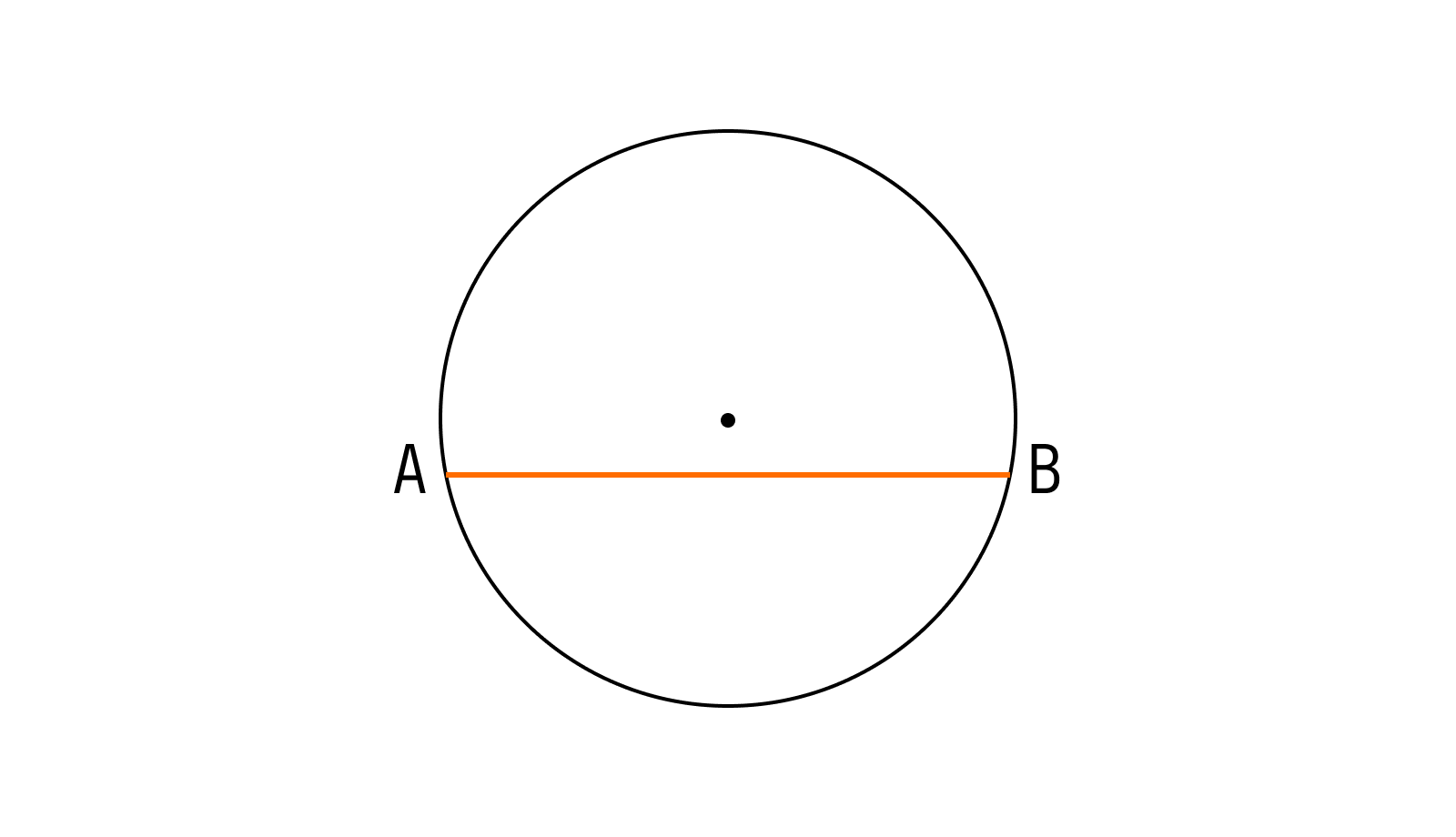
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

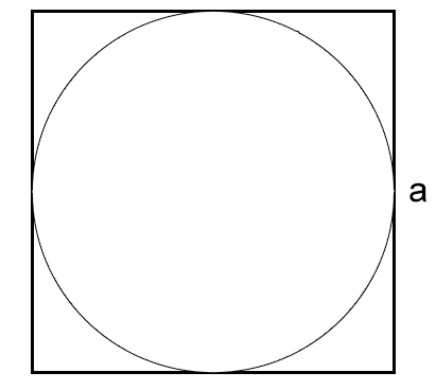
Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

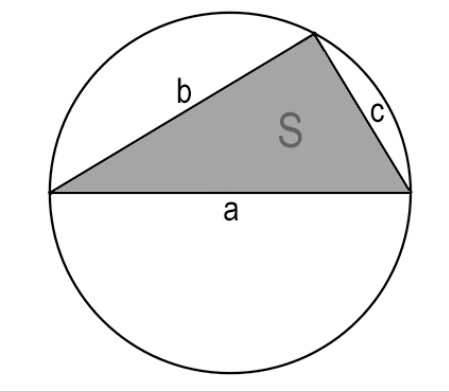
Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

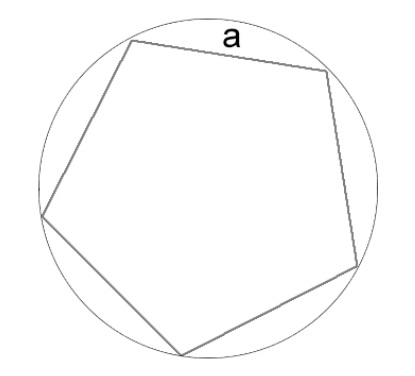
Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

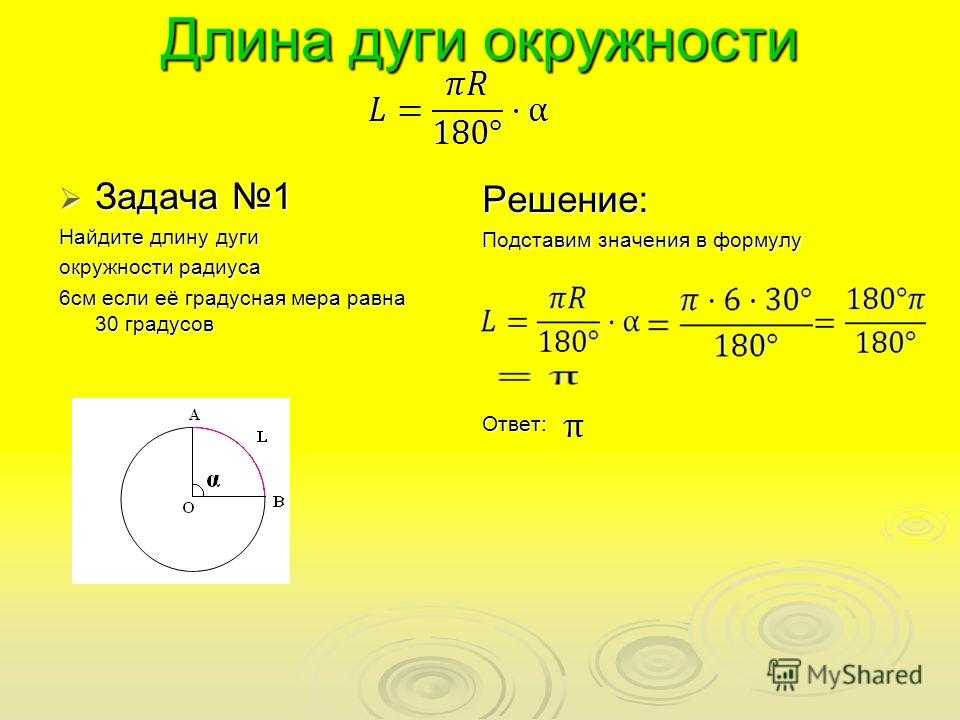
Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

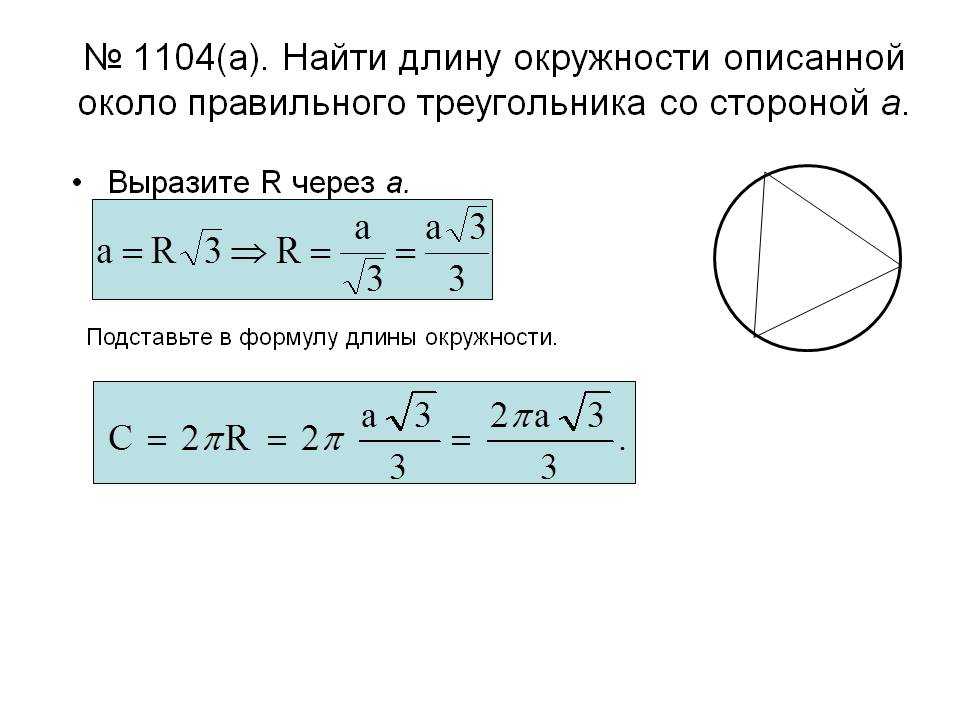
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною дм

Обучение на курсах по математике поможет закрепить полученные знания на практике.

Источник

Калькулятор длины окружности

Скачать, сохранить результат

Выберите способ сохранения

Информация

Длина окружности находится очень просто, но, тем не менее, это является основой геометрии и изучается еще средней школе. Формула длины окружности имеет следующий вид:

P=2πr,

где P – длина окружности;

π – константа, которая всегда равна 3,14;

r – радиус окружности, длину которой необходимо найти.

Однако, существует еще одна формула и наш калькулятор длины окружности также её использует. Данная формула имеет следующий вид:

P=πd, где

P – длина окружности;

π– константа, которая всегда ровна 3,14;

d – диаметр окружности, длину которой необходимо найти.

Разница между формулами в том, что в первой длина окружности находится через радиус, который умножается на два, а во второй используется сразу диаметр.

Данные формулы применяются в многих сферах жизни человека. От производства каких-либо товаров, до строительства небоскребов. Лица, ответственные за проектирование зданий несут огромную ответственность за верность их расчетов, которые буквально влияют на человеческие жизни и их сохранность. Для того, чтобы избежать человеческого фактора в процессе расчета точных показателей, был создан онлайн калькулятор, в котором легко находится длина окружности через радиус или диаметр.

Благодаря данному инструменту Вы сможете не только получить информацию о том, как найти длину окружности, но и рассчитать её без каких-либо усилий. Калькулятор гарантирует предельную точность расчетов и Вам не нужно задаваться как узнать верны ли расчеты. На сайте показаны формулы, по которым считает калькулятор и это подтверждает то, что любой расчет будет верным.

Источник

Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.

Вычислить периметр круга через:Длина радиуса R:

Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.

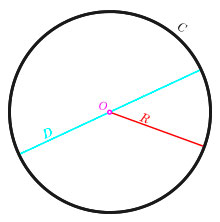
Длина окружности всегда равна числу π (Пи)

Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…

Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.

Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».

Иными словами Пи ≈ 3,14 диаметрам круга или окружности.

Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна

P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр

Источник

Длина окружности круга через диаметр: онлайн-калькулятор

На нашем сайте собраны программы, которые помогают сделать расчеты по алгебре, геометрии. Сервис содержит расчеты по всем основным темам. Вы сможете найти длину окружности, периметры, объемы фигур, а также получить решение более сложных задач. Для этого достаточно только ввести данные. Сразу после этого будут доступны действия и ответ.

Использование автоматических подсчетов избавляет от промежуточных ошибок, неточностей при переводе из одних величин в другие. Чтобы получить точный ответ, воспользуйтесь нашим сервисом.

Нахождение длины окружности через диаметр. Онлайн-калькулятор

Программа позволяет рассчитать длину окружности по формуле:

Любой пользователь может производить расчеты на сайте без регистрации и платежей. Это создано для повышения уровня образования, возможности повысить успеваемость по математике, самостоятельно разобраться в непонятной теме.

Кто чаще всего пользуется нашим сервисом:

Источник

Определение длины окружности через диаметр или радиус

Вычисление длины окружности

При решении задач и в повседневной жизни можно встретить множество предметов круглой формы, в связи с чем возникает необходимость в их измерении. К примеру, для расчета объема материала, необходимого для производства круглого стакана определенного размера, потребуется построить и найти длину его окружности.

Окружность представляет собой замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки.

Рассматриваемая в рамках этого определения точка является центром окружности. Если соединить центр с любой точкой, принадлежащей окружности, то получится радиус. Радиусом также называют длину данного отрезка.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

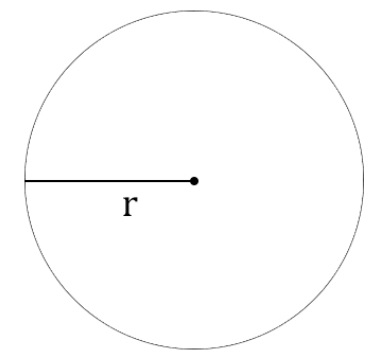
Радиус окружности является прямым отрезком, который выходит из центра окружности и проведен до ее границы.

Таким образом, радиус окружности соединяет ее центр с точкой, расположенной на этой окружности. Для обозначения радиуса используют r.

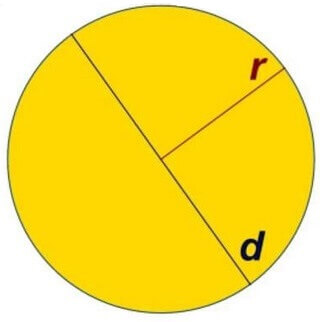
Диаметр окружности – является прямым отрезком, который соединяет две точки, расположенные на границе окружности, и проходит через центр этой окружности.

Данный параметр обозначают D или d.

Как рассчитать через диаметр или радиус

Длина окружности также является периметром этой окружности. Для расчета длины или периметра круга необходимо знать диаметр или радиус.

Формулы для вычисления длины окружности:

\(L = 2 \pi rL=2\pi r\)

где L – является длиной окружности;

D – определяется, как диаметр окружности;

r – представляет собой радиус окружности;

\(\pi\) – это число Пи, равное примерно 3,14.

Исходя из представленных формул для расчета длины окружности, можно вывести соотношение радиуса и диаметра окружности:

Основные формулы с пояснением

Обладая информацией о радиусе и диаметре окружности, достаточно просто рассчитать ее длину. Однако не во всех задачах присутствуют эти данные. Есть ряд примеров, в которых определить длину окружности необходимо с помощью параметров другой геометрической фигуры.

Вычисление длины окружности через площадь круга

В том случае, когда известна площадь круга, можно рассчитать длину окружности по формуле:

где \(\pi\) — является числом пи, значение которого равно 3,14;

S — определяет площадь круга

Расчет длины окружности через диагональ вписанного прямоугольника

В задачах можно встретить примеры вписанного в окружность прямоугольника.

В этом случае длина окружности рассчитывается по формуле:

где \( \pi\) — является числом пи, значение которого равно 3,14;

d — является диагональю рассматриваемого прямоугольника.

Как вычислить длину окружности через сторону описанного квадрата

В том случае, когда окружность вписана в квадрат с прямыми углами, сторона которого известна, можно определить длину этой окружности.

где \(\pi \) — является числом пи, значение которого равно 3,14;

a — определяет длину стороны квадрата

Расчет длины окружности с помощью сторон и площади вписанного треугольника

Предположим, что в окружность вписан треугольник. Если имеется информация о всех его трех сторонах, а также площади, то можно рассчитать длину окружности, оперируя следующей формулой:

где \(\pi\) — математическая константа со значением 3,14;

a — является первой стороной треугольника;

b — является второй стороной треугольника;

с – является третьей стороной треугольника;

S – определяется, как площадь рассматриваемого треугольника.

Способ нахождения длины окружности при известной площади и полупериметру описанного треугольника

Представим, что в какой-то треугольник вписана окружность. Известно значение площади треугольники и его полупериметр. Необходимо рассчитать длину окружности. Следует заметить, что периметром треугольника называют сумму всех его сторон, а полупериметр составляет половину этой суммы. Таким образом, для нахождения полупериметра нужно определить периметр треугольника и разделить его на два.

Формула расчета длины окружности:

где \(\pi\) — математическая константа со значением 3,14;

S — является площадью треугольника;

p — представляет собой полупериметр треугольника.

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Когда в окружность вписан правильный многоугольник, в первую очередь стоит сосчитать количество его сторон. Также требуется знать длину стороны этой геометрической фигуры. Стороны правильного многоугольника одинаковы, как у квадрата. В этом случае формула для расчета длины окружности имеет вид:

где \(\pi\) — математическая константа со значением 3,14;

a — это сторона многоугольника;

N — определяет количество сторон многоугольника.

Примеры решения задач

Необходимо рассчитать, какова длина окружности, если ее диаметр составляет 5 см.

При известном диаметре окружности можно рассчитать ее длину с помощью формулы:

Подставив известные из условия задачи значения, получим:

\(L = \pi D = 3,14 * 5 = 15,7\) (см)

Ответ: длина окружности равна 15,7 см.

Требуется определить длину окружности, описанной вокруг правильного треугольника, сторона которого составляет \(a=4\sqrt<3>\) дм.

Радиус окружности составляет:

При подстановке переменных формула будет изменена:

При известном радиусе окружности можно рассчитать длину рассматриваемой окружности, используя соответствующую формулу:

\(L = 2 \pi r=2 \pi *4=2*3,14*4=25,12\) (дм)

Ответ: длина окружности составляет 25,12 дм.

Дана окружность, радиус которой равен 2 см. Требуется рассчитать длину окружности.

L = 3.14 * 4 = 12,56 (см)

Ответ: длина окружности равна 12,56 см.

Имеется окружность с радиусом 3 см. Необходимо определить длину данной окружности.

L = 3.14 * 3 = 9,42 (см)

Ответ: длина окружности составляет 9,42 см.

Источник

Длина окружности: онлайн-калькулятор

Вы будете перенаправлены на Автор24

На этой странице вы узнаете, как посчитать длину окружности зная радиус или диаметр, а также сможете рассчитать длину круга с помощью онлайн-калькулятора.

Для того чтобы рассчитать длину окружности через радиус, введите заданное значение радиуса в поле для ввода.

Расчёт длины окружности

$L = 2 \cdot π \cdot R$, здесь

$R$ — радиус окружности;

Задача

Решение:

Воспользуемся вышеприведённой формулой:

$L = 2 \cdot 3,14 \cdot 50 ≈ 314,16$ мм.

Данный ответ совпадает с решением онлайн-калькулятора, а значит, он найден верно.

Длину круга через диаметр можно посчитать с помощью следующего онлайн-калькулятора.

Длина окружности через диаметр

Через диаметр длину окружности рассчитывают по формуле:

$L = π \cdot d$, где

$d$ — диаметр окружности.

Рассмотрим также пример как найти окружность зная диаметр.

Задача

Решение:

$L = 3,14 \cdot 7 = 21,99$ см.

Проверим наш расчёт длины окружности по диаметру с помощью калькулятора онлайн. Результаты совпадают, а значит — ответ найден верно.

Если вы задаётесь обратным вопросом, например, как определить диаметр трубы по длине окружности, то для измерений длины окружности можно использовать нитку, которую нужно аккуратно проложить по окружности.

Затем получившийся отрезок нужно измерить с помощью линейки.

При необходимости более точных расчётов для измерения диаметра следует использовать штангенциркуль.

Нужны еще материалы по теме статьи?

Воспользуйся новым поиском!

Найди больше статей и в один клик создай свой список литературы по ГОСТу

Источник

Длина окружности.

Как найти длину окружности? Найдите длину окружности по радиусу или диаметру заполнив поля в калькуляторе ниже.

Длина окружности равна 2ПиR

1. Сложнее найти длину окружности через диаметр, по этому сначала разберём этот вариант.

Пример: Найдите длину окружности диаметр которой равен 6 см. Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.

После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.

2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см

Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.

Онлайн калькулятор длины окружности

Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.

Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.

Источник

Как зная диаметр круга, найти длину окружности?

По какой формуле высчитать? Если знаю только, что диаметр равен 40 см.

Существует одна и на все времена формула для определения длины окружности и это все проходили по геометрии.

По условию задания нам известен диаметр D=40 см.

Решение: L = Пи*D = 3,14 х 40 = 125,6 см.

Ответ: длина окружности равна 125,6 сантиметра.

Диаметр круга: D (BC) = 40 см

Диаметр равняется двум радиусам: D = 2R (или АС+АВ)

Формула для вычисления длины окружности: L = 2πR или L = πD

Значение постоянного числа π ≈ 3,14

D = 40 см

Решение:

Длина окружности L = 3,14 × 40 ≈ 125,6 см

Если вычисления производить на калькуляторе, на котором встроено значение π, т. е. использовать клавишу с буквой π, то результат будет несколько иной:

L = π × 40 = 125,6637061436 ≈ 125,7 см

Ответ: при диаметре круга 40 см длина окружности приблизительно равна 125,7 см.

Источник

Длина окружности

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.

Определение длины окружности

Формула расчёта длинны окружности

Произвести расчёт окружности можно по следующей формуле:

r – радиус окружности

D – диаметр окружности

L – длина окружности

Пример нахождения длинны окружности

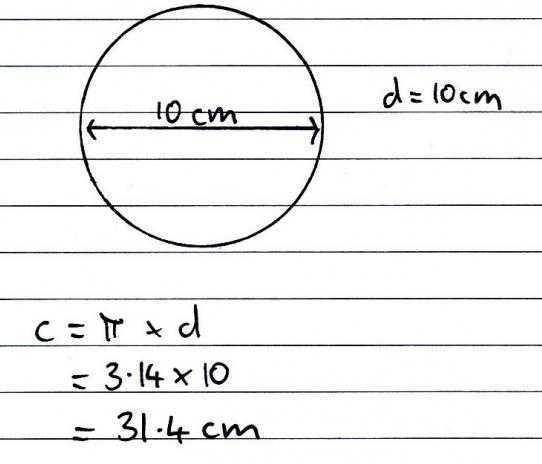
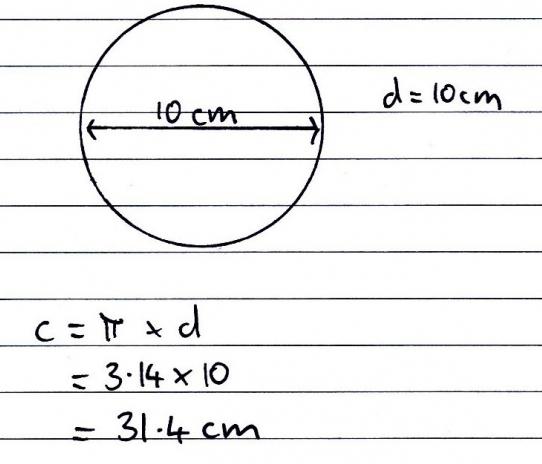
Вычислить длину окружности, имеющей радиус 10 сантиметров.

Формула для вычисления дины окружности имеет вид:

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 31,4 сантиметра

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

Источник

Как найти длину окружности и площадь круга

Соавтор(ы): Grace Imson, MA. Грейс Имсон — преподаватель математики с более чем 40 годами опыта. В настоящее время преподает математику в Городском колледже Сан-Франциско, ранее работала на кафедре математики в Сент-Луисском университете. Преподавала математику на уровне начальной, средней и старшей школы, а также колледжа. Имеет магистерскую степень по педагогике со специализацией на руководстве и контроле, полученную в Сент-Луисском университете.

Количество источников, использованных в этой статье: 7. Вы найдете их список внизу страницы.

Количество просмотров этой статьи: 203 869.

Окружность – это плоская замкнутая кривая, все точки которой равноудалены от центральной точки. [1] X Источник информации Длина окружности (С) – это длина замкнутой кривой, которая и образует окружность. [2] X Источник информации Площадь круга (А) – это величина пространства, которое ограничено окружностью. [3] X Источник информации Площадь круга и длина окружности вычисляются по формулам, в которых присутствует радиус (или диаметр) окружности и число «пи».

Источник

Длина окружности, онлайн калькулятор через диаметр или радиус

Калькулятор

Варианты расчёта длины окружности через радиус или диаметр

Тут выбираем вариант расчёта окружности

Визуально выглядит так:

Вводим диаметр или радиус:

Длина окружности (круга) равна :

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом

Как рассчитать длину окружности по диаметру или радиусу, формулы

Найти длину окружности по диаметру или радиусу можно в нашем онлайн калькуляторе

Источник

Длина окружности

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня у нас очередная математическая тема. Ее проходят в 6-м классе. Называется она – ДЛИНА ОКРУЖНОСТИ.

Эта важная величина для решения многих задачек. В том числе и во время Единого госэкзамена.

Так что наша статья будет крайне полезна школьникам-выпускникам. А для всех остальных это хороший повод освежить свои знания.

Что такое окружность

Но для начала напомним, что называют окружностью.

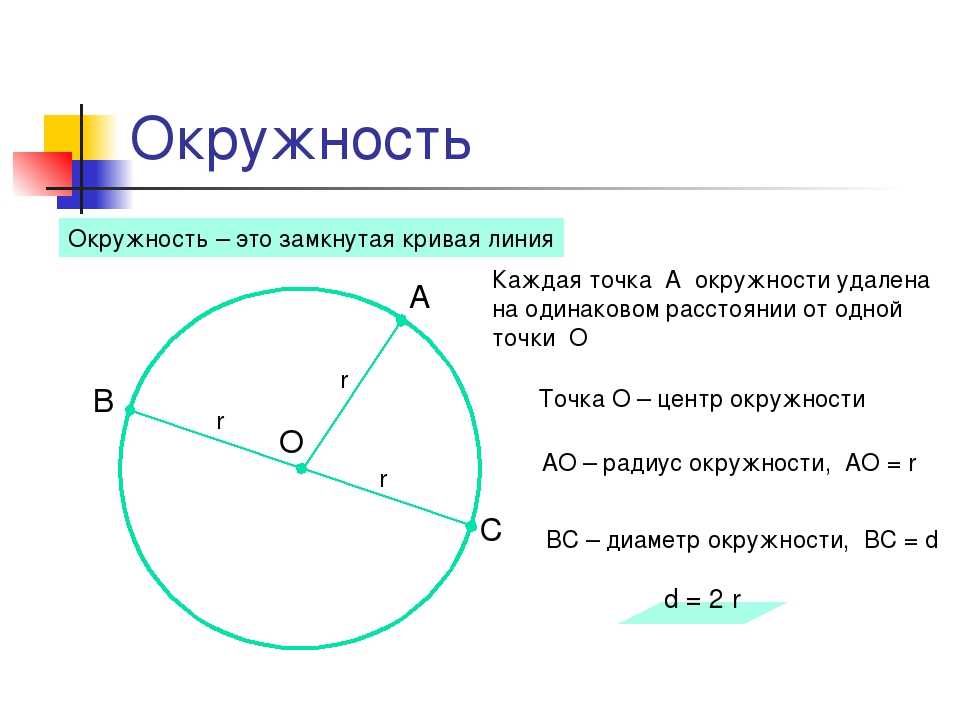
Окружность – это кривая замкнутая линия, которая состоит из множества точек. И эти точки находятся на одном расстоянии от центра окружности.

Определение несколько «тяжеловатое», но это официальная формулировка, которая также приводится в школьных учебниках. Графически все выглядит гораздо проще.

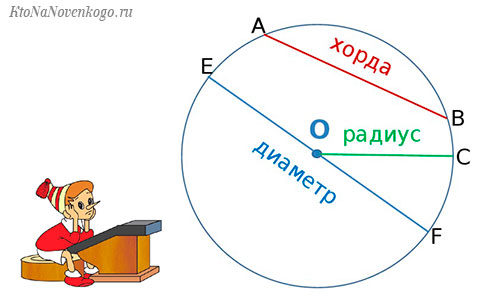
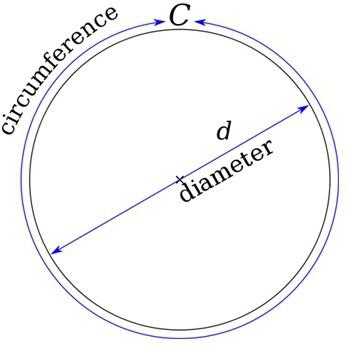
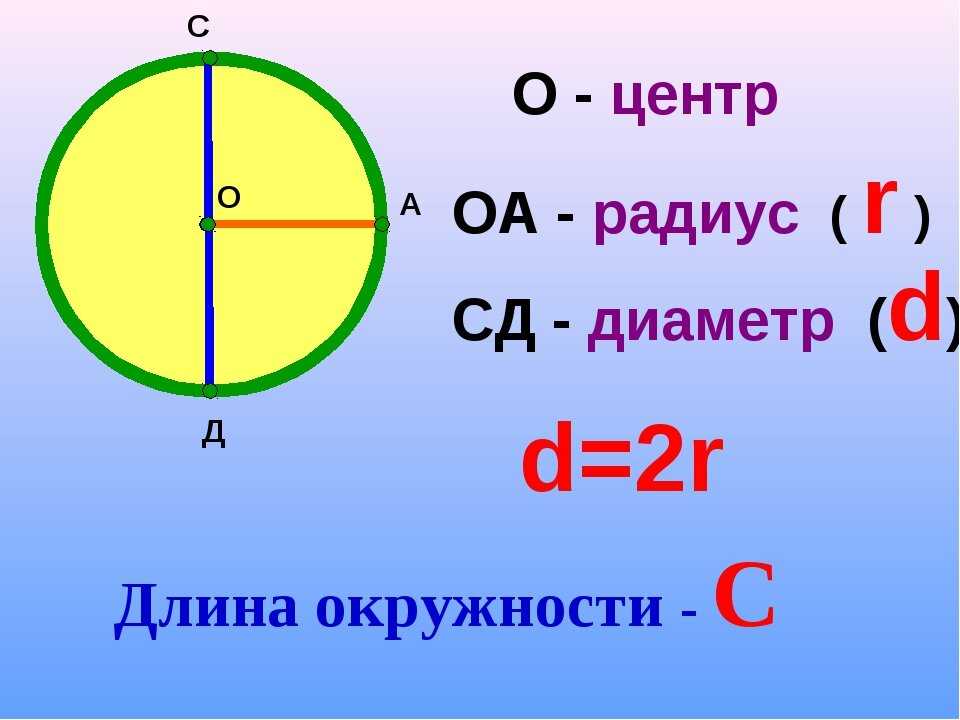
Вот пример окружности, у которой все точки на кривой «С» равноудалены от центра «О».

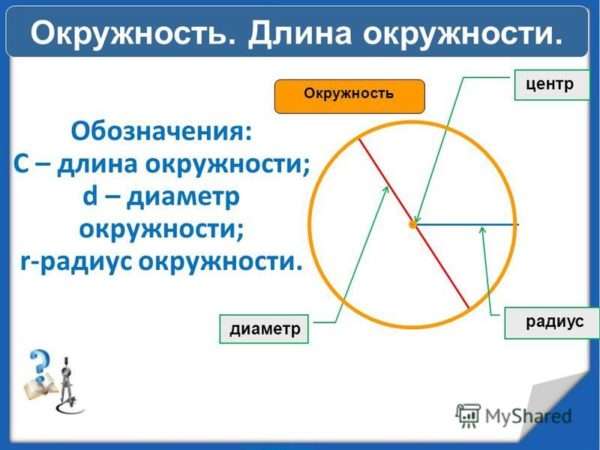
Кстати, расстояние от центра до границы окружности называется радиус и обозначается он буквой «R».

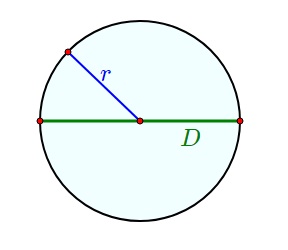
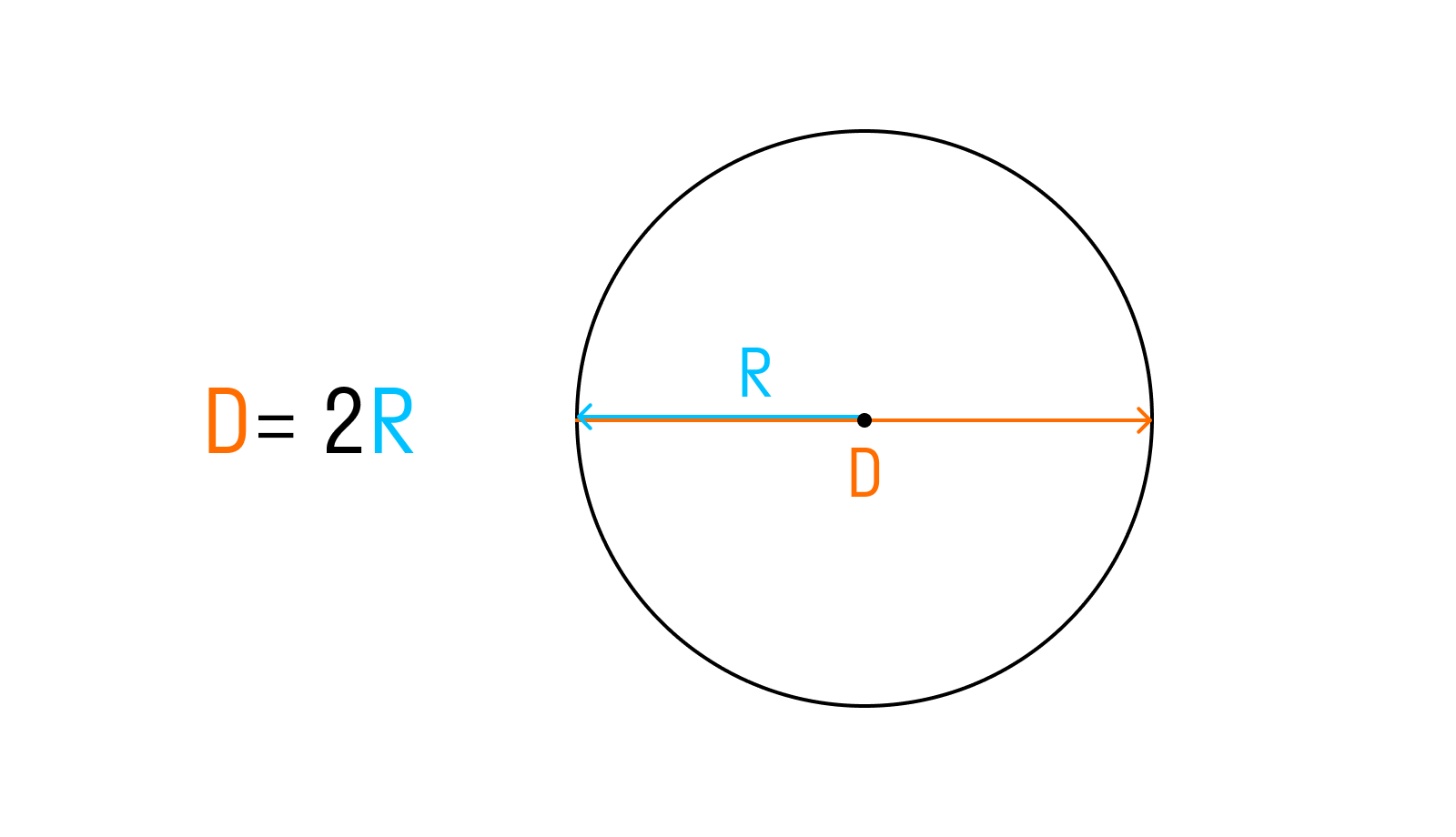
А отрезок, который соединяет две точки на окружности и проходит через ее центр – это диаметр «D». И, как всем известно, диаметр – это два сложенных радиуса (D = 2R).

Интересный факт! Точка тоже является в некотором роде окружностью. В математике ее называют «окружностью нулевого радиуса».

А чтобы начертить правильную окружность, нужно воспользоваться специальным прибором – циркулем. Им же можно нарисовать и окружность нужного радиуса.

Длина окружности через диаметр

Зачем мы так подробно рассказали о самой окружности, ее радиусе и диаметре? Все просто – без них не обойтись при расчете длины окружности.

Эту зависимость заметили еще в Древнем Египте. Тогдашние математики были весьма продвинуты в различных инженерных расчетах. Достаточно вспомнить, насколько надежно построены пирамиды. Им более 5 тысяч лет, а кажется, что простоят еще столько же и даже больше.

Так вот, египтяне определили, что соотношение длины окружности и ее диаметра – величина постоянная.

Другими словами, если взять совершенно разные по размерам окружности, а потом поделить их длины на их же диаметры, то получится одно и то же число.

У египтян это было число 3. Но впоследствии было получено более точное значение, которое равно 22/7 или 3 целых и 1/7.

Так появилась математическая постоянная «ПИ». Сейчас это один из столпов науки, с помощью которого решаются многие задачи.

Кстати, само название «пи» происходит от греческого слова «περιφέρεια», что как раз переводится как окружность. А «περίμετρος» — это диаметр.

Этими обозначениями и воспользовался математик Леонард Эйлер, когда в 1737 году представил научному сообществу число «пи», обозначив его изначально буквой выше упомянутых слов.

И сейчас уже каждый школьник знает, что число «пи» равно 3,14. Это значение взято за базовое, хотя на самом деле в нем бесконечное количество знаков после запятой.

Формула длины окружности

Ну а теперь главный вывод из этого исторического экскурса. Согласно вычислениям еще древнеегипетских ученых, формула длины окружности выглядит так:

Но чаще всего эту формулу принято писать без знаков умножения:

Формула эта единственная. И других возможностей рассчитать длину окружности — нет. Хотя ее можно представить, как диаметр умноженный на ПИ, но это уже банальность.

Вот и все, что мы хотели рассказать по этой теме, а более подробно смотрите в приведенном видеоролике:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Вот объясните, как длина окружности может иметь конечное значение, если её можно разбить на отрезки, а те отрезки на ещё меньшие отрезки и так до бесконечности. Как то, что состоит из бесконечного количества отрезков, может быть конечно?

Источник

Вычисление радиуса: как найти длину окружности зная диаметр

Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого….

Основные понятия и определения

Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.

Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.

Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях! Диаметр окружности.

Нахождение длины окружности и её площади

Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r. Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два.

Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r.

Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!

Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу. Получится: l = 2*П*r = 2*r*П = П*d.

Из курса математики известно, что формула, описывающая площадь окружности, имеет вид: s = П*r^2.

Теперь перепишем предыдущую формулу, чтобы найти площадь окружности через её диаметр. Получим,

s = П*r^2 = П*d^2/4.

Одним из самых сложных заданий в данной теме является определение площади круга через длину окружности и наоборот. Воспользуемся тем, что s = П*r^2 и l = 2*П*r. Отсюда получим r = l/(2*П). Подставим полученное выражение для радиуса в формулу для площади, получится: s = l^2/(4П). Абсолютно аналогичным способом определяется и длина окружности через площадь круга.

Определение длины радиуса и диаметра

Важно! Прежде всего узнаем, как измерить диаметр. Это очень просто проводим любой радиус, продлеваем его в противоположную сторону до пересечения с дугой. Циркулем отмеряем полученное расстояние и с помощью любого метрического инструмента узнаем искомое!

Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.

Мы уже знаем как из длины окружности можно найти её диаметр, точно также найдём и радиус.

l = 2*П*r, отсюда r = l/2*П. Вообще, чтобы узнать радиус, его нужно выражать через диаметр и наоборот.

Пусть теперь требуется определить диаметр, зная площадь окружности. Используем то, что s = П*d^2/4. Выразим отсюда d. Получится d^2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).

Это интересно! Первый признак равенства треугольников: доказательство

Решение типовых заданий

Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон

Окружность, диаметр, хорда геометрия 7 класс

Заключение

Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Источник

Как найти и чему будет равна длина окружности

Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.

Определение окружности

Существует несколько определений этой геометрической фигуры.

Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.

Определение окружности

Формулы

Чтобы посчитать периметр круга, необходимо знать его диаметр (D) или радиус (R), который равняется D, деленному на 2.

Как вычислить длину окружности через радиус? Это делается по простой формуле:

где L – искомая величина,

π – число пи, примерно равное 3,1413926.

Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.

Обозначения

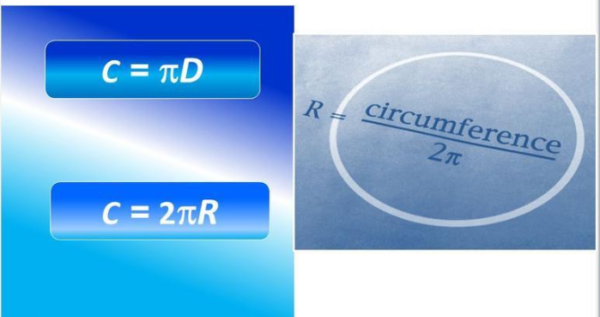
Для нахождения через диаметр существует следующая формула:

Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.

Если уже дана площадь круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда

L = 2πR = 2π√(S/π) = 2√(Sπ).

Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)

Резюмируя, можно сказать, что существует три основных формулы:

Формулы

Число пи

Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.

Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.

Это интересно! Урок геометрии: как найти по формуле периметр треугольника

Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.

Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.

Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.

Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.

Полезное видео: длина окружности

Практическое применение

Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:

L = πD = 3,14 * 20 = 62,8 см.

Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:

L = 2πR = 2 * 3,14 * 13 = 81,68 м.

Полезное видео: круг радиус, диаметр, длина окружности

Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.

Источник

Длина окружности

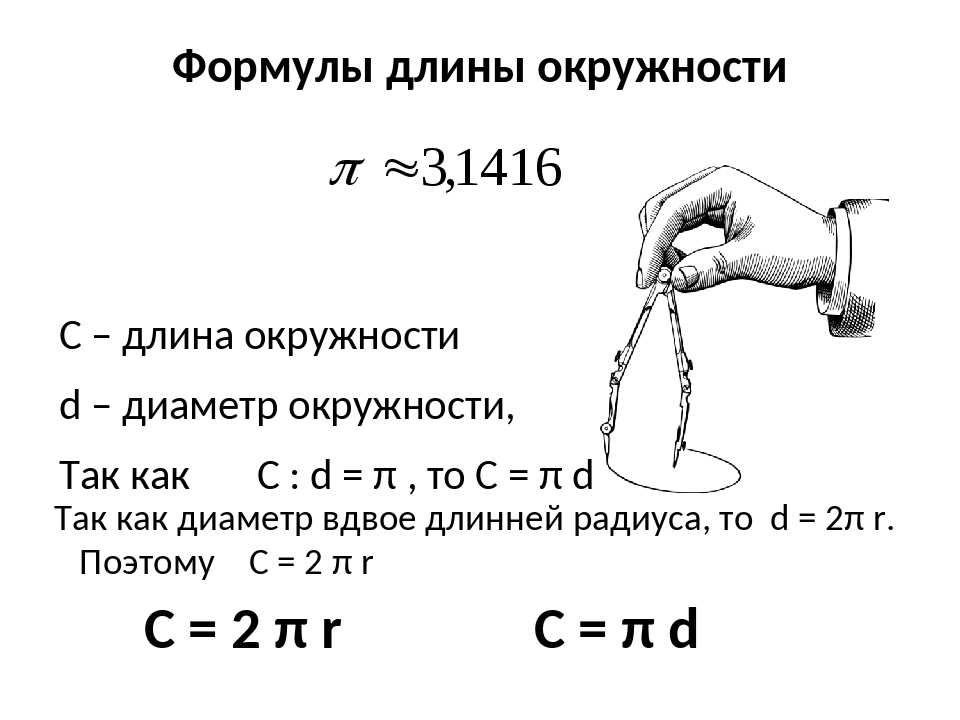
Запишите формулу для вычисления длины окружности через диаметр. Формула имеет вид: C = πd, где C — длина окружности, d — диаметр окружности. То есть длина окружности равна произведению диаметра на число пи (π примерно равно 3,14).
X
Источник информации

Подставьте данные вам значения в формулу и найдите длину окружности.
X
Источник информации

Запишите формулу для вычисления длины окружности через радиус. Радиус равен половине диаметра, а диаметр, соответственно, — двум радиусам (2r). Тогда формула имеет вид: C = 2πr, где C — длина окружности, r — радиус окружности. То есть длина окружности равна удвоенному произведению радиуса на число пи (π примерно равно 3,14).
X
Источник информации

Подставьте данные вам значения в формулу и найдите длину окружности. Например, вы вырезаете полоски декоративной бумаги, чтобы красиво обернуть вокруг кексов при подаче на стол. Радиус кекса равен 5 см. Подставьте это значение в формулу.
X
Источник информации

Что такое окружность и где она встречается?

Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

Примеры заданий

Условие. Узнать длину окружности, радиус которой равен 5 см.

Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).

Ответ: l = 31,4 см.

Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.

Ответ: r = 200 мм.

Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.

Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.

Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.

Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

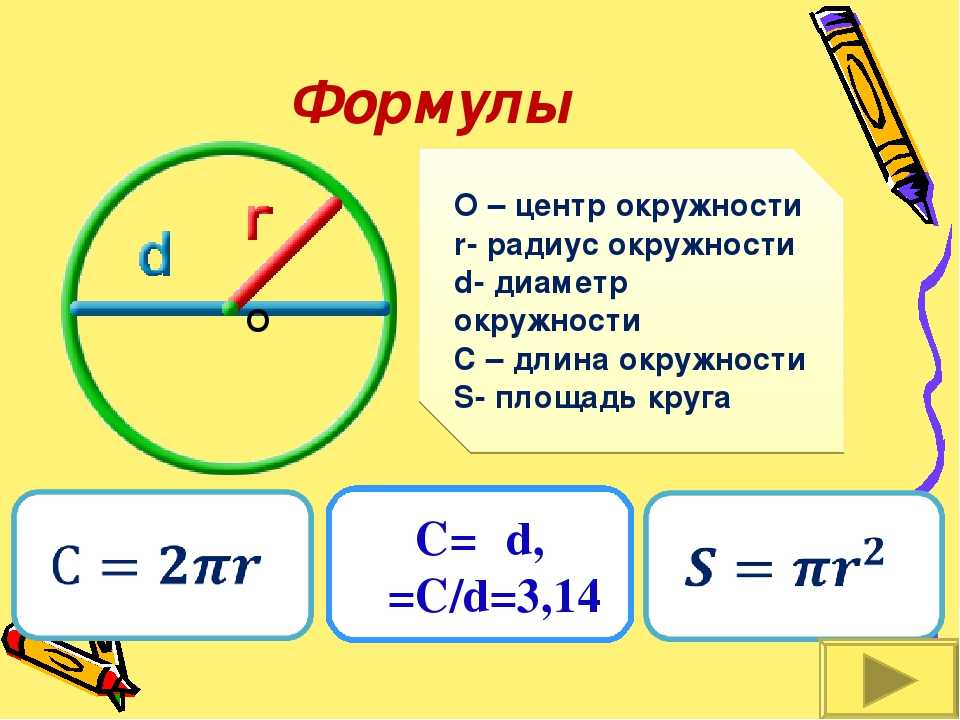
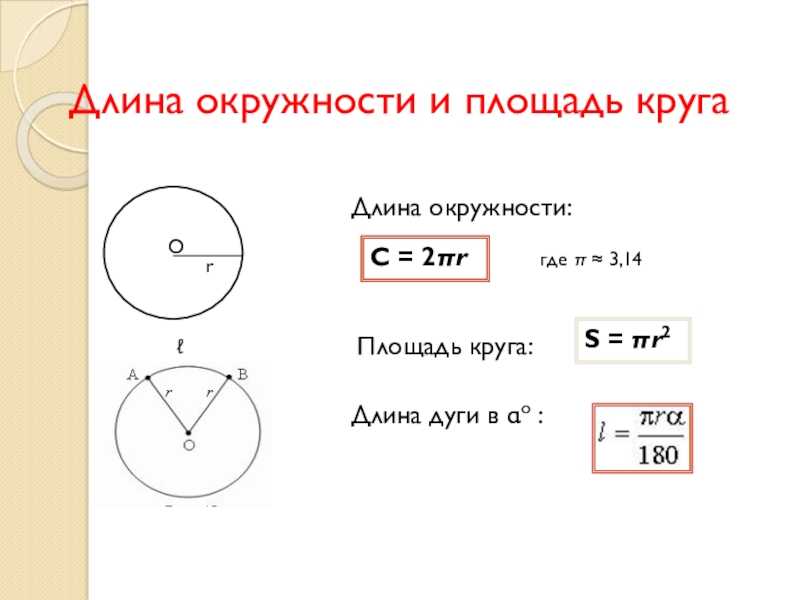
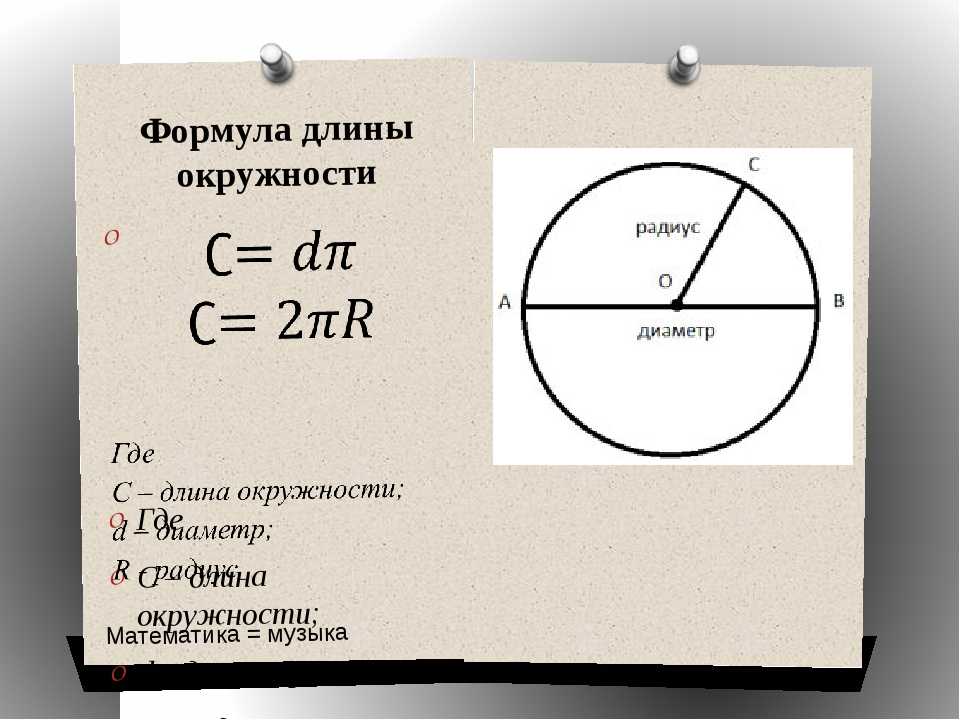
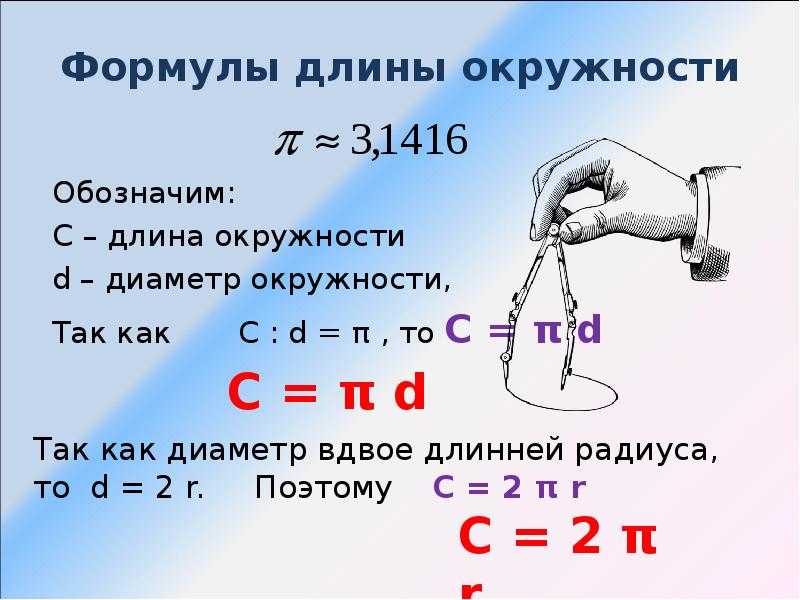
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.

Ответ: Белка пробегает 6,28 м.

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 139 человек(а). Количество просмотров этой статьи: 746 448.

English:Calculate the Circumference of a Circle

Français:calculer la circonférence d’un cercle

Italiano:Calcolare la Circonferenza di un Cerchio

Español:calcular la circunferencia

Deutsch:Einen Kreisumfang berechnen

Português:Calcular a Circunferência de um Círculo

Nederlands:De omtrek van een cirkel berekenen

Bahasa Indonesia:Menghitung Keliling Lingkaran

Čeština:Jak vypočítat obvod kruhu

हिन्दी:गोलाकार चीजों की परिधी ज्ञात करें

العربية:حساب محيط دائرة

Tiếng Việt:Tính Chu vi Hình tròn

Türkçe:Bir Dairenin Çevresi Nasıl Hesaplanır

فارسی:محیط یک دایره را محاسبه کنیم

Окружность. Круг

А сейчас познакомимся с самой совершенной фигурой, как считал древнегреческий математик Пифагор. Ответьте на вопрос: «Какие известные вам геометрические плоские фигуры не содержат углов?»

Правильно, круги, а еще окружности.

Совершенная форма этой геометрической фигуры привлекает внимание художников, дизайнеров, архитекторов. Они используют её в своих изделиях для украшения

Ограда на набережной реки Невы в Санкт-Петербурге

Назовите предметы из обычной жизни, которые по форме похожи на эти фигуры.Правильно, круглые очки. Вы очень внимательные ребята.

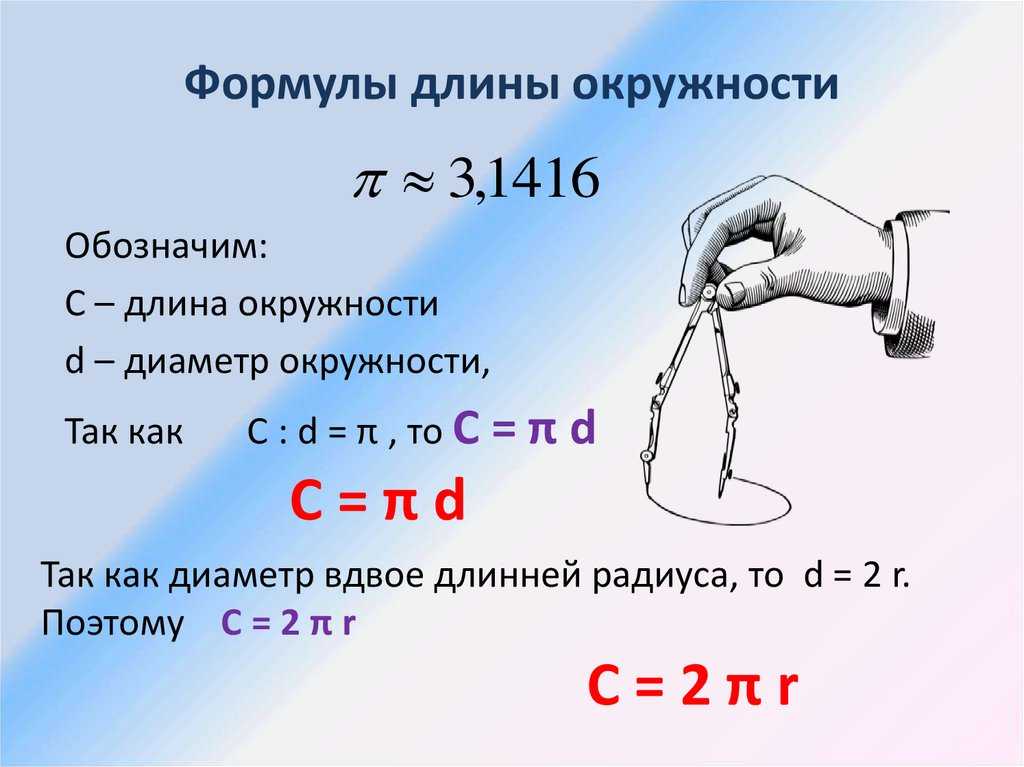
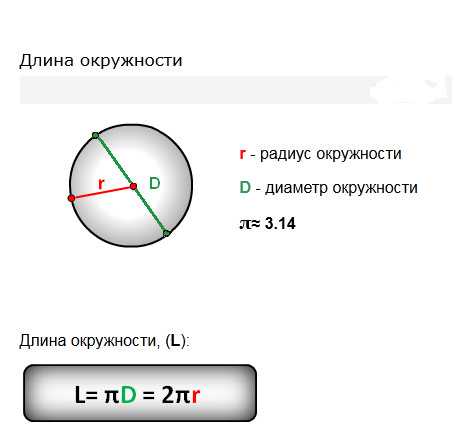
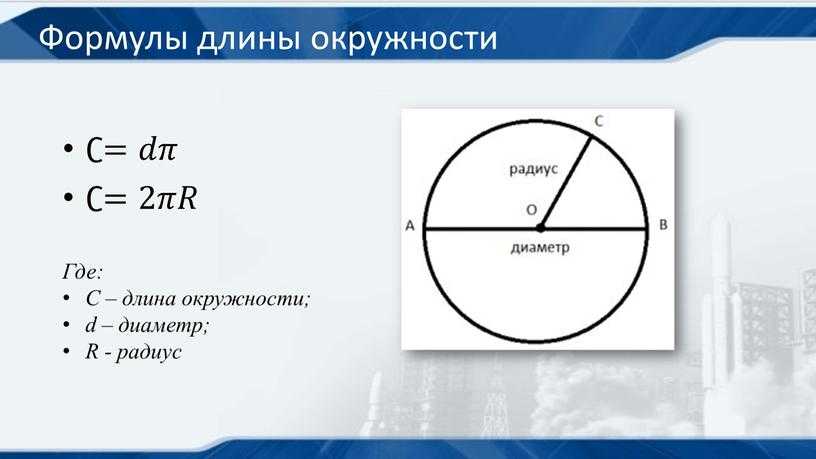
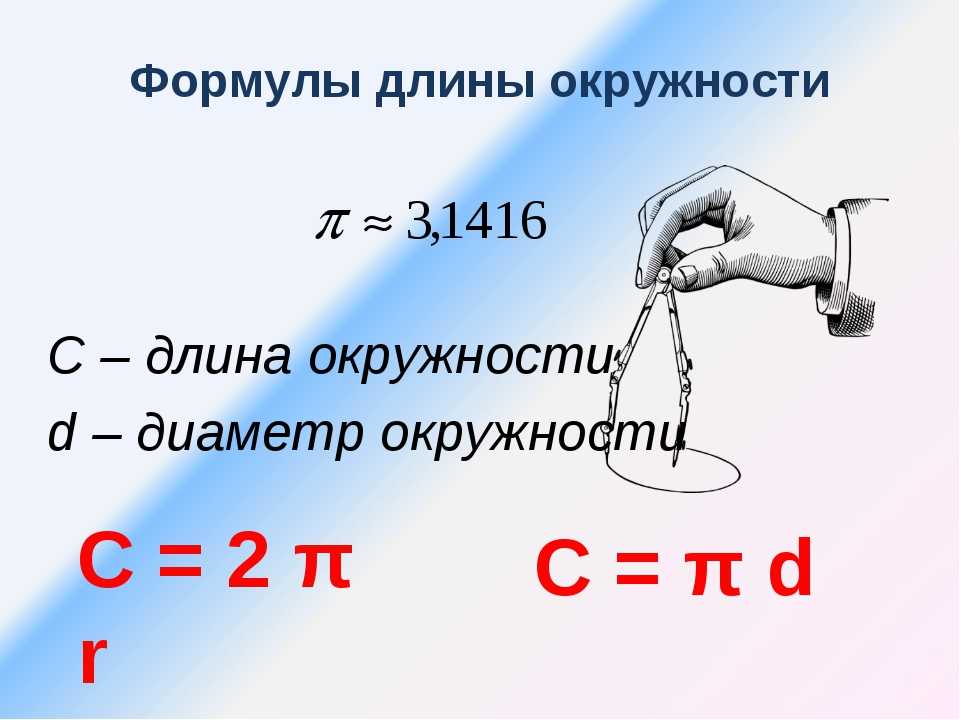
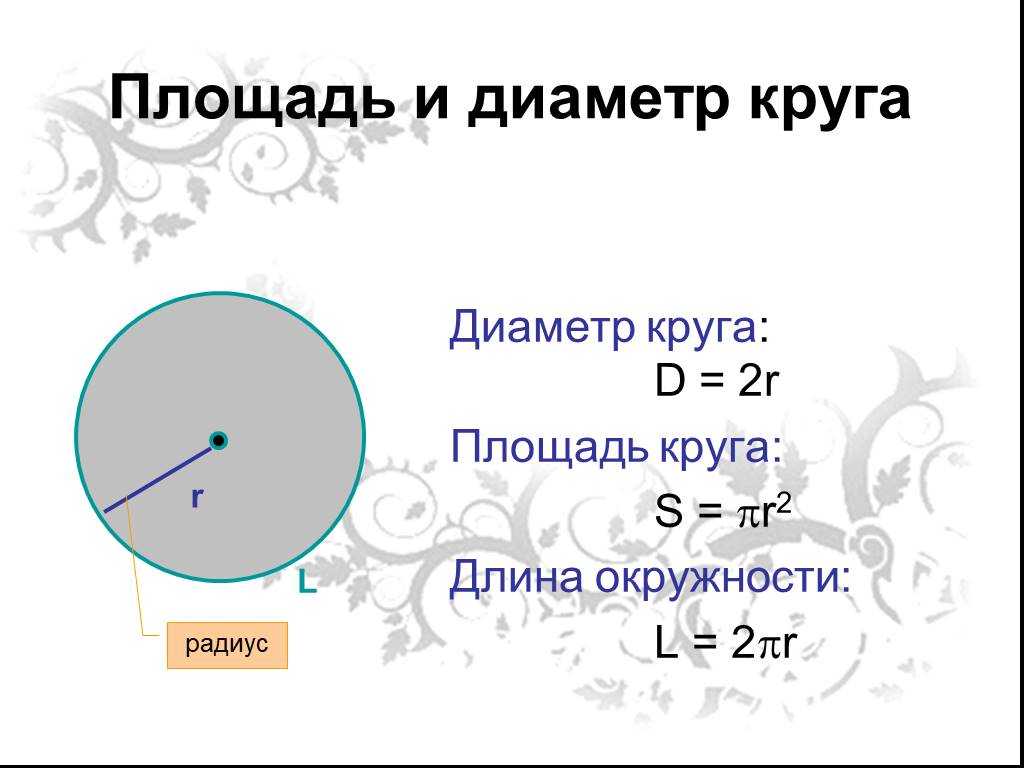
Посмотрите на рисунок. Назовите окружности и круги.

Но как начертить такие ровные окружности? Приглашаю на помощь лучшего друга.

Эх, циркач, удалой.
Чертит круг одной ногой,
А иглой — проткнет бумагу,
Он воткнется — и ни шагу.

Знакомьтесь, ребята, к нам пришел новый житель страны Геометрии – чертежный инструмент. Он поможет разобраться, как изобразить круг.

Привет, я циркуль. Мое имя произошло от старинного латинского слова «циркулюс», что означает круг.

Давайте потренируемся чертить циркулем:

Линию, нарисованную грифелем циркуля, называют окружностью.

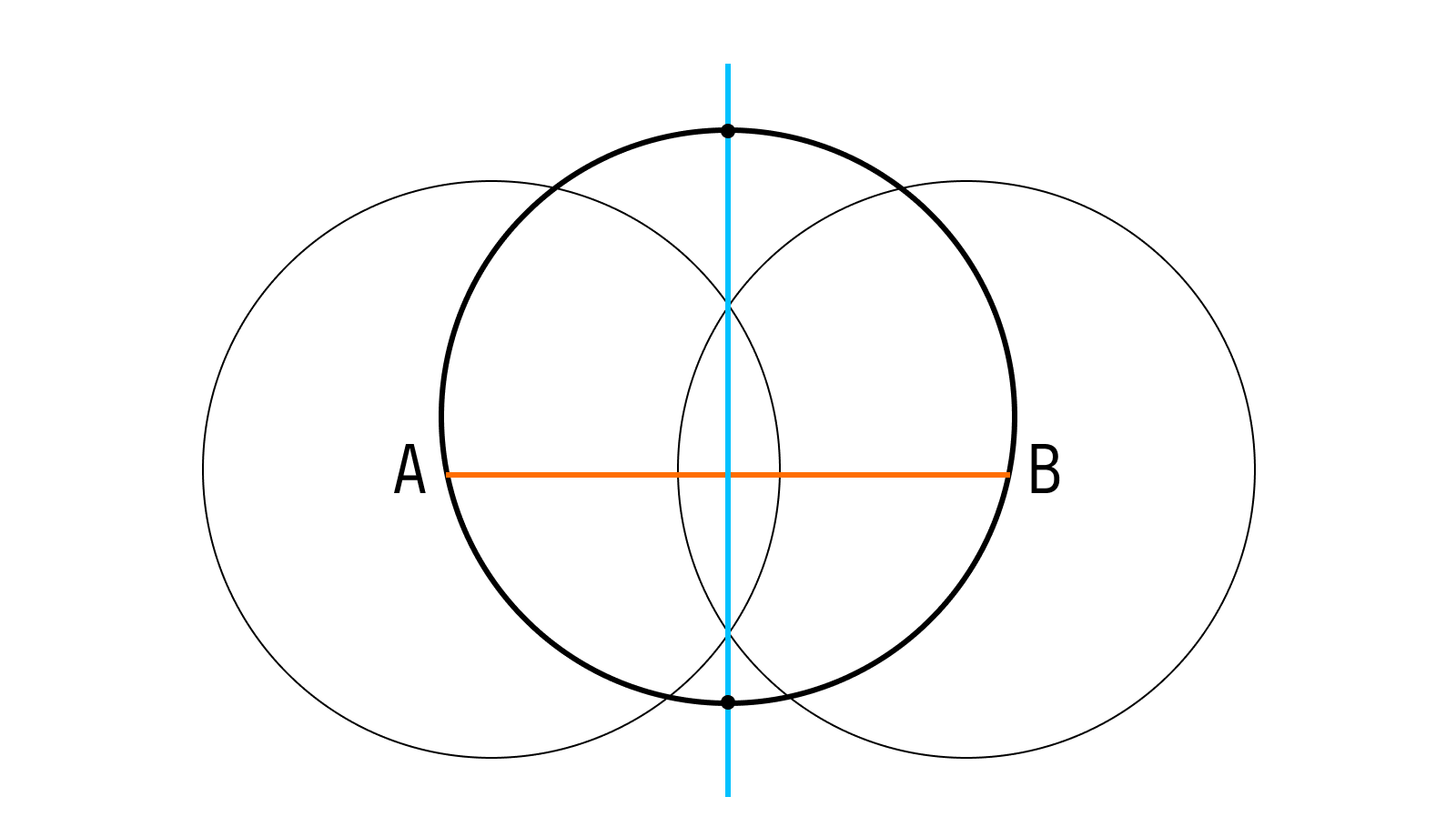
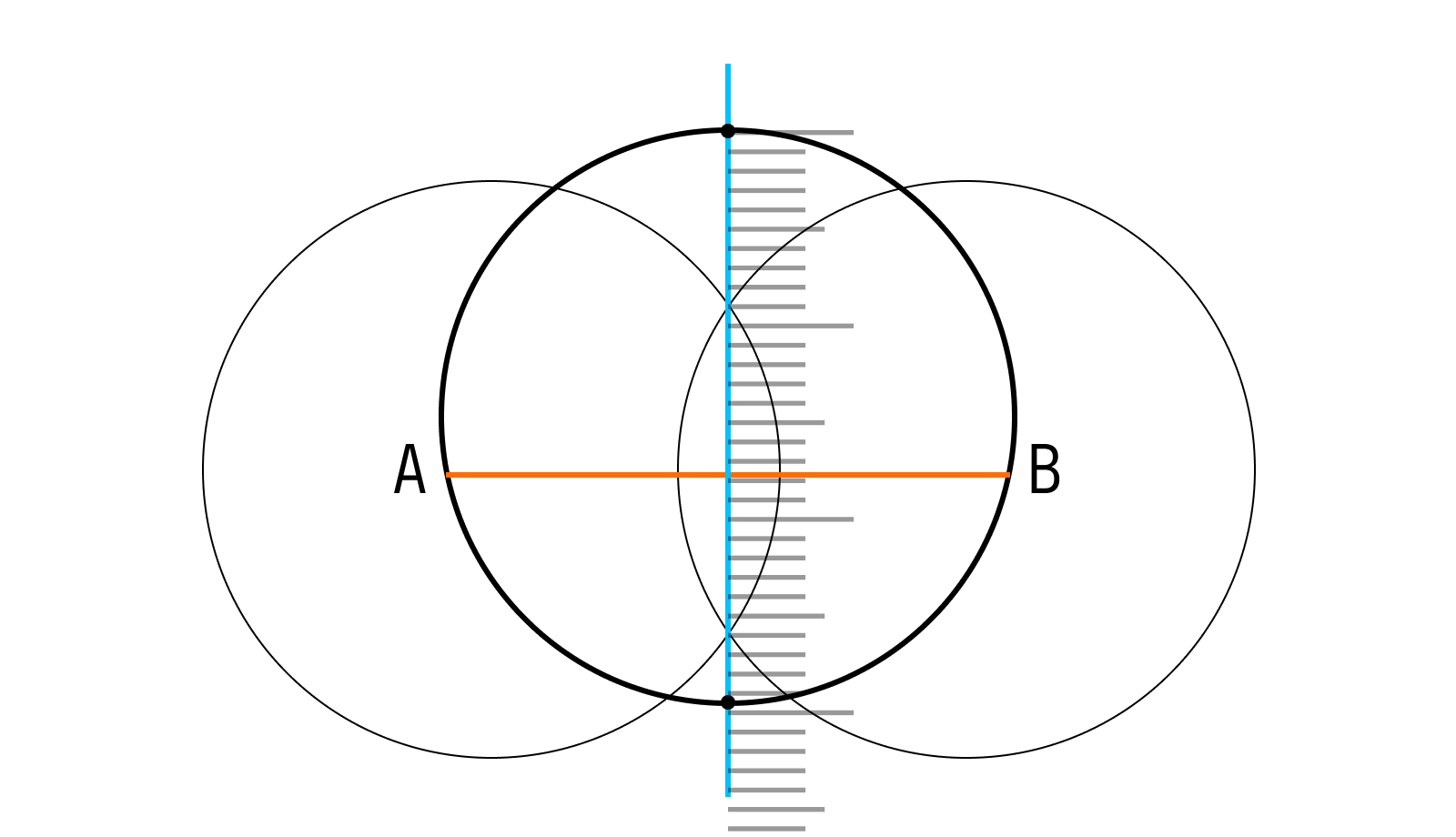
Точки на окружности А и В расположены от центра на равном расстоянии. Их соединяет отрезки ОА и ОВ – называются радиусами окружности.

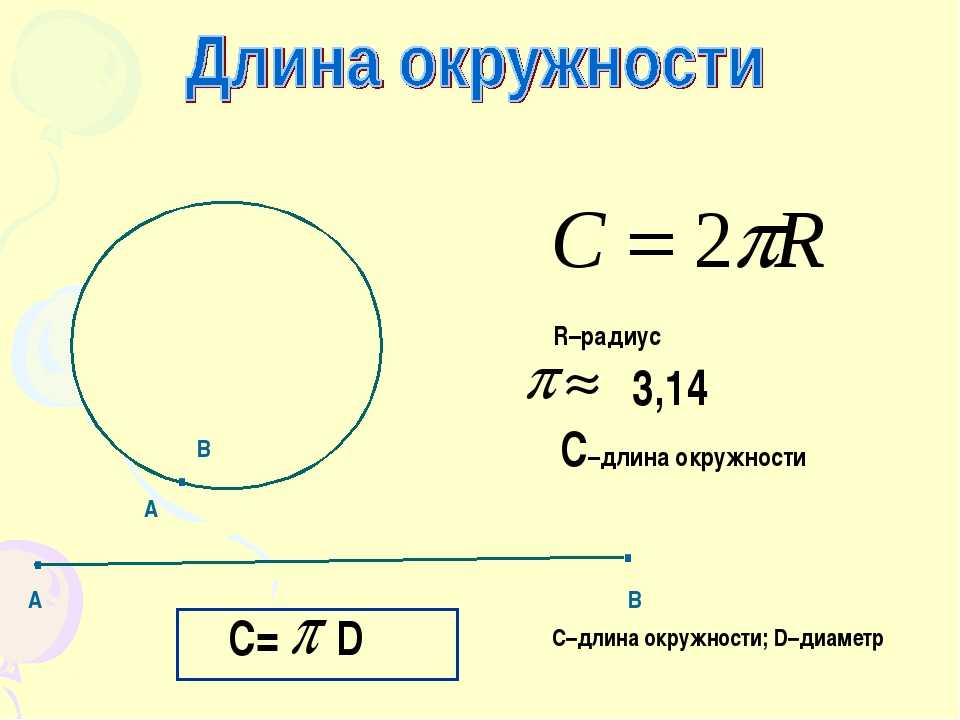
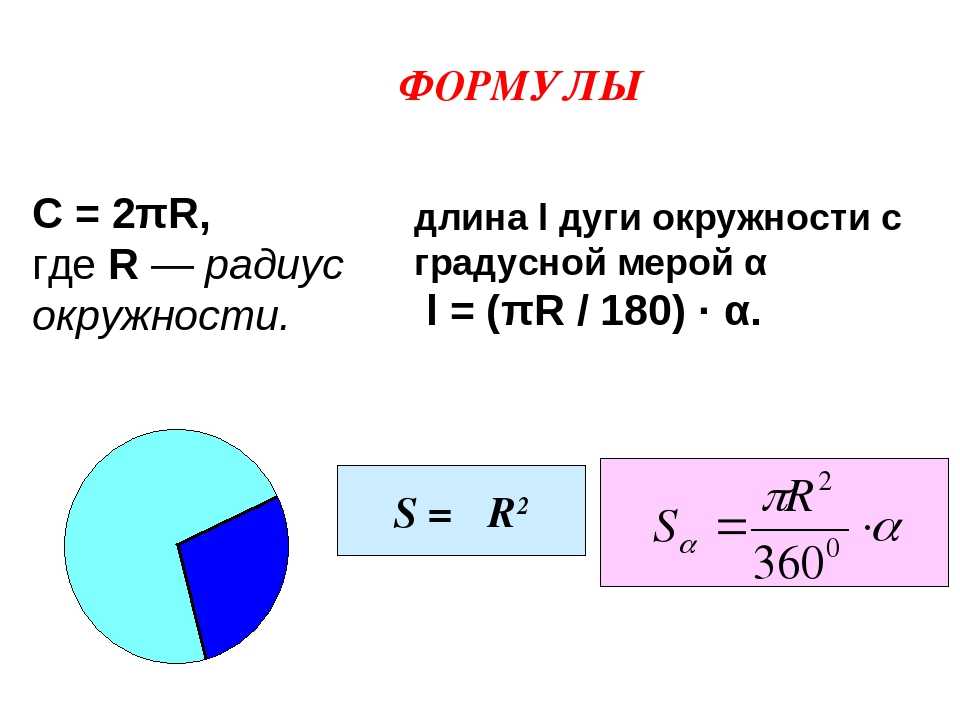
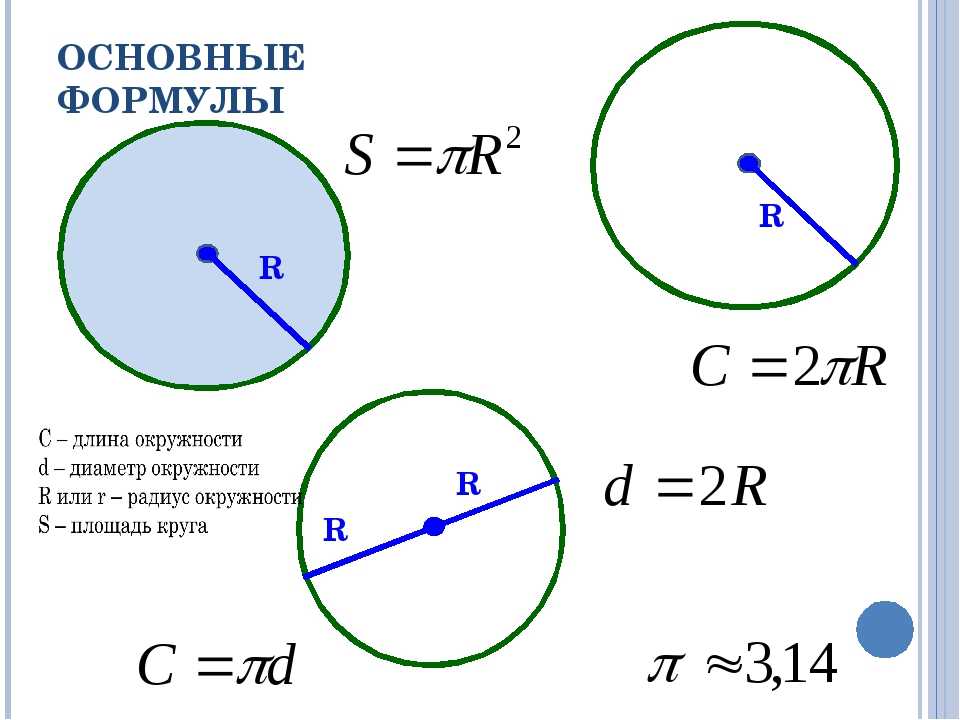
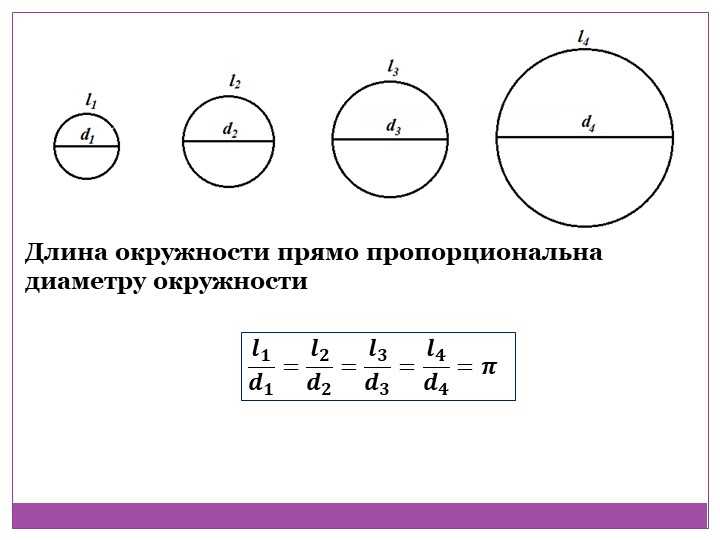
Продлите по линейке отрезок ВО поперек всей окружности. Вы начертили диаметр окружности— отрезок ВС. Он прошел через центр и соединил 2 точки на окружности В и С.

Как вы думаете, сколько диаметров можно провести в одной окружности?

Совершенно верно — сколько угодно, как говорят математики — бесконечное число.

Посмотрите на колесо от велосипеда.

Втулка — это центр, а спицы напоминают радиусы и диаметры.

Если величину диаметра умножить на 3, мы получим примерную длину окружности. Точную формулу вычисления вы узнаете в 7 классе на уроках геометрии, а также, что такое вписанная и описанная окружности.

А сейчас возьмите альбомный лист, начертите окружность и по этой границе аккуратно вырежьте фигуру. Её можно закрасить любым цветом, например, синим, как на рисунке. Это круг — часть плоскости, ограниченная окружностью.

У круга есть площадь. Окружность вырезать невозможно, потому что это просто замкнутая кривая линия вокруг круга — его граница.

На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь закрашенной части фигуры.

Рассуждайте так: на рисунке закрашена четвертая доля фигуры. Значит надо выполнить деление.

Источник

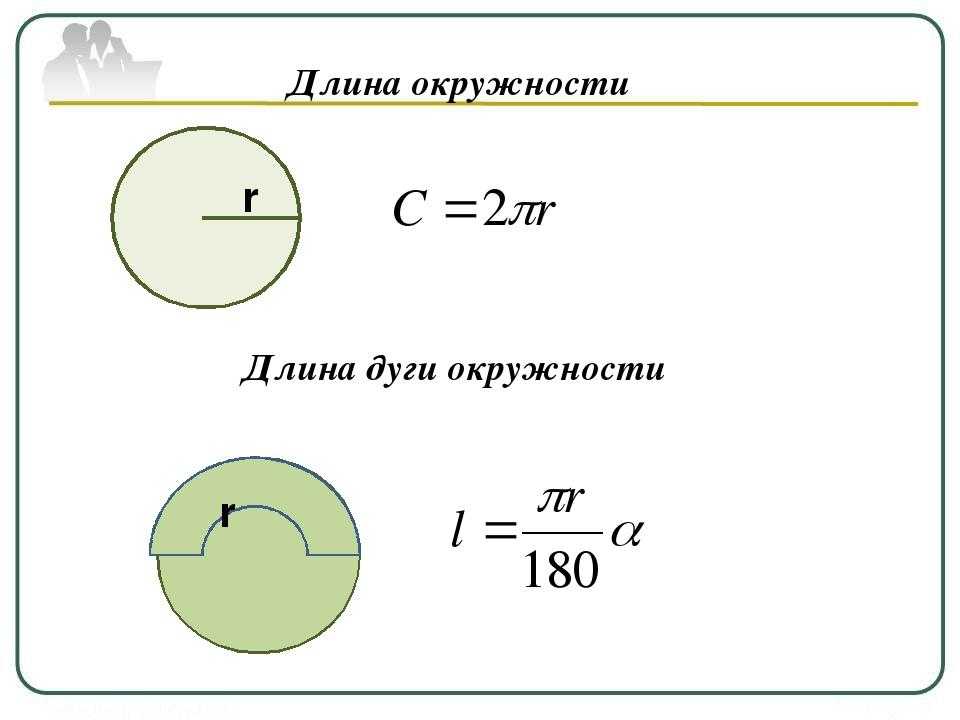
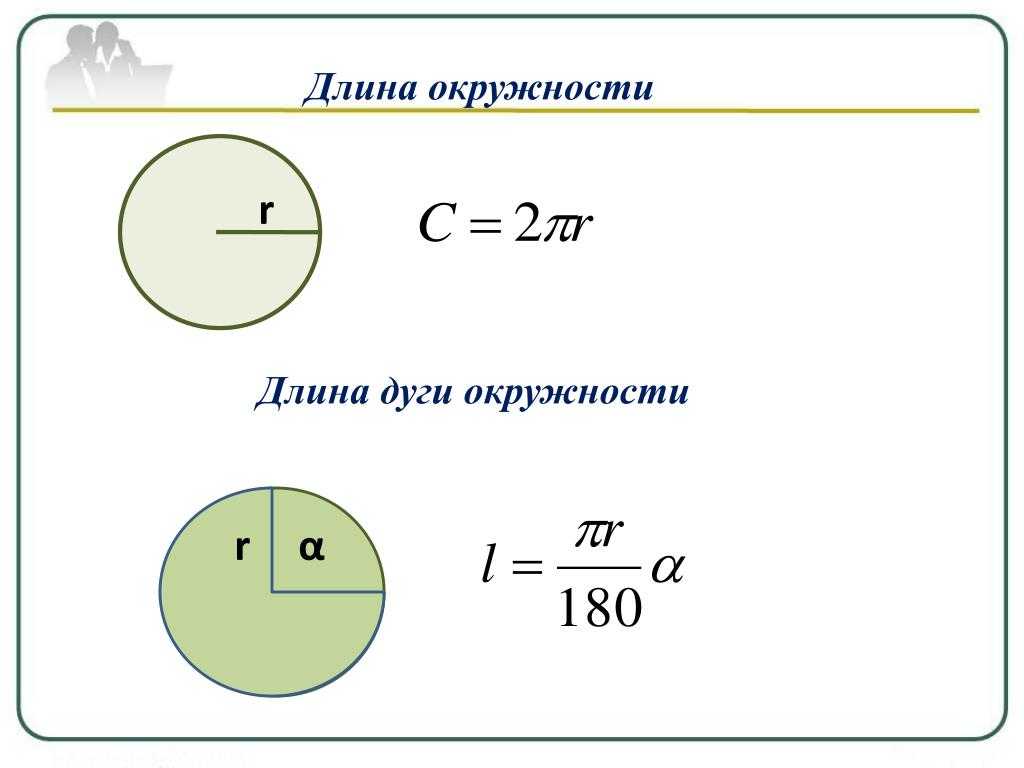
Как найти длину окружности

Формула

То есть нужно воспользоваться одной из формул:

$l=2 \pi r \text < или >l=\pi d$

Примеры вычисления длины окружности

Задание. Найти длину окружности, диаметр которой равен 3 см.

Решение. Для вычисления длины заданной окружности воспользуемся формулой

Подставляя в неё исходные данные, получим:

$l=3 \pi \approx 3.14 \cdot 3=9.42$ (см)

Для нахождения длины рассматриваемой окружности воспользуемся формулой

$l=2 \cdot \pi \cdot 4 \approx 8 \cdot 3,14=25,12$ (дм)

Остались вопросы?

Здесь вы найдете ответы.

Площадь круга (S) рассчитывается путем умножения числа Пи на длину его радиуса (R), возведенную в квадратную степень (S = ПR²). Из указанного равенства можно выразить радиус:

Если избавиться от квадратной степени, то получится:

Длина окружности (L) рассчитывается путем умножения числа Пи на длину радиуса, и последующего умножения на два полученного в результате числа:

Если R = √(S/П), то L = 2П*√(S/П)

Длина окружности (L) представляет собой число, которое получено в результате умножения числа Пи на диаметр данной окружности:

В конкретном случае:

L = 3,14*2 = 6,28 см.

Ответ: Длина окружности с диаметром 2 см составляет 6,28 см.

Известно, что длина окружности (L) рассчитывается путем умножения на два произведения числа Пи и длины ее радиуса (R). Формула выглядит так:

Из данной формулы можно выразить радиус

R = 12пи/2пи = 6 см

Радиус окружности, описанной около квадрата, равен 6 см.

Теперь можно вычислить сторону квадрата, вокруг которого описана данная окружность. Ее длина составляет R корней из 2:

а = 6 корней из 2.

Рассчитываем длину малого радиуса (r), который равен половине длины стороны квадрата:

r = а/2 = 6 корней из 2/2 = 3 корней из 2.

Длина окружности, вписанной в квадрат, рассчитывается по той же формуле:

L = 6 корней из 2 Пи.

Радиус окружности, равный 30 см, обозначается как R.

Площадь окружности можно найти, умножив число Пи на квадрат длины ее радиуса:

Подставим в формулу известные величины:

S = π*30² = 900π см. кв.

Длина окружности обозначается как С и рассчитывается путем умножения на 2 произведения числа Пи и ее радиуса:

Снова подставляем в формулу величины, которые известны:

C = 2π*30 = 60π см

Ответ: Площадь окружности равна 900π см², а ее длина составляет 60π см.

По условию задачи известно, что треугольник является правильным, что означает равенство всех его трех сторон. В данном случае его площадь может быть рассчитана по следующей формуле:

Зная площадь, мы получаем возможность вычислить длину стороны а. Она будет равна ± √48. Учитывая то, что сторона не может быть отрицательной величиной, можно говорить о том, что сторона а равна √48.

После того как длина стороны стала известна, можно приступить к вычислению площади описанной и вписанной окружности. Для этого не достает еще одного элемента – длины радиуса.

Радиус описанной окружности (R) равен длине стороны треугольника, разделенной на √3:

Радиус вписанной окружности (r) можно получить, разделив на 2 радиус описанной окружности:

Вычисленные длины радиусов вписанной и описанной окружностей позволяют определить ее длину ℓ, которая равна произведению числа Пи и радиуса окружности, умноженному на 2:

В нашем случае длина описанной окружности рассчитывается как:

Длина вписанной окружности будет составлять:

В условии задачи говорится о том, что радиус окружности R равен 12 см. Ее длина может быть вычислена посредством умножения на 2 произведения длины радиуса и числа Пи:

Известно, что число Пи – это константа, равная 3,14. Тогда длина окружности (С)высчитывается следующим образом:

Площадь окружности можно найти, умножив число Пи на длину ее радиуса, возведенную в квадратную степень:

S=πR²=3,14*12²=3,14*144=452,16 см кв.

По условию задачи длина окружности равна 20 Пи см. Зная формулу, по которой вычисляется длина окружности, можно записать следующее равенство:

Можно сократить Пи в обеих частях записанного равенства, в результате чего получится, что:

Теперь высчитаем, чему равна длина радиуса окружности:

Длина диаметра равна длине радиуса, умноженной на 2:

D = R*2 = 10*2 = 20 cм.

Полная градусная мера любой окружности равна 360 градусов. В случае, описанном в задании, градусная мера окружности составляет 120 градусов, что равно 1/3 части 360 градусов. Это позволяет сделать вывод о том, что длина окружности (L) может быть рассчитана следующим образом:

L = 6Пи * 3 = 18Пи

Формула, по которой вычисляется длина окружности, выглядит так:

Из данной формулы можно выразить радиус (R):

В заданном случае длина радиуса будет равна:

Обозначим прежнюю длину окружности как L, а новую – как L₁. Тогда можно записать следующее равенство:

Прежний радиус окружности примем за R, а новый ее радиус, который получится в результате увеличения длины, обозначим как R₁. Для того чтобы вычислить ее значение, следует сначала записать формулу, по которой вычисляется прежняя длина данной окружности:

Тогда формула для вычисления новой длины окружности будет иметь такой вид:

Отнимем от новой длины старую, и в итоге получим:

Перенесем 2Пи из левой части равенства в правую:

Ответ: В результате увеличения длины окружности на 9,42 см ее радиус станет больше на 1,5 см.

Радиус окружности, которая вписана в правильный треугольник, обозначим r. Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:

В случае треугольника, все стороны которого одинаковы, радиус вписанной в него окружности равен третьей части высоты, являющейся также и медианой.

Площадь правильного треугольника рассчитывается так:

Sтр = (1/2)*(2r/tg30)*3r = (1/2)*(2r√3)*3r = 3√3r².

Перенесем πr² из левой части равенства в правую, изменив его знак на противоположный:

Вынесем в правой части равенства r² за скобки. То же самое сделаем с числом 9 в левой части равенства:

Таким образом, радиус окружности равен корню квадратному из 9:

Обозначим радиус второй окружности буквой х. В данном случае радиус первой окружности нужно обозначить как 5х. Известно, что разница между длинами диаметров двух окружностей равна 240 мм. На основании этого можно составить следующее равенство:

5х-х=240:2, что равно 4х=120

Теперь можно найти значение х:

Таким образом, радиус второй окружности равен 30 мм. Это позволяет вычислить радиус первой окружности, который в 5 раз больше радиуса второй из них:

Длина дуги обозначена как L. В качестве обозначения ее градусной меры используется α. Через R обозначена длина радиуса данной окружности. Формула расчета длины дуги выглядит так:

Это же равенство может быть переписано следующим образом:

Отсюда выведем радиус:

Длина окружности (L) равна произведению числа Пи и радиуса, которое умножено на 2:

Согласно заданию, длина дуги равна 3,14, что равно значению константы Пи.

Дуга способна поместиться в длине окружности 2 пи r/пи =2 r раз

Подставив в равенство значения, которые известны, мы получим:

Длина окружности будет равна:

Сократим 2Пи в каждой из частей равенства и получим, что:

Для решения поставленной задачи следует записать формулу расчета площади круга:

Эта величина указана в задании, и составляет 169Пи. Это значит, что:

Можно сократить одинаковый множитель Пи в обеих частях равенства:

Длина окружности обозначена С. Она считается по следующей формуле:

Длина радиуса уже известна, и ее можно подставить в формулу расчета длины окружности:

С = 2* π*13 = 26π см.

Известно, что площадь круга представляет собой величину, равную длине стороны этого квадрата, возведенной во вторую степень Sкв = а². Это значит, что в данном случае а² = 36 дм. Для того чтобы найти значение а, нужно извлечь квадратный корень из 36:

Длина диагонали (d) квадрата считается по приведенной ниже формуле:

Радиус (R)окружности, которая описана около квадрата, равен половине длины ее диагонали:

Площадь круга можно посчитать, умножив число Пи на квадрат его радиуса:

S = πR² = π · (3√2)² = 18π дм. кв.

Длина окружности рассчитывается посредством умножения на два числа Пи, после чего полученное число умножается на длину радиуса окружности:

C = 2πR = 2π · 3√2 = 6√2π дм.

Ниже записана формула, которая используется для того, чтобы рассчитать длину окружности:

где Пи – это константа, равная 3,14, а d – это диаметр окружности.

Отношение длины первой окружности к длине второй окружности равно отношению их диаметров:

В условии сказано, что длина первой окружности С = 3,5 дм. Таким образом:

C1 = 5/7 *C = 5/7 * 3,5 = 2,5 дм.

Для того чтобы узнать длину окружности (C), следует воспользоваться формулой, предназначенной для ее расчета. Она выглядит так:

Если подставить в эту формулу величины, которые даны по условию задачи, то получим:

Ответ: Длина окружности равна 88 см.

Длина окружности равна длине ее половины, умноженной на 2. Это значит, что в данном случае нужно умножить число 25,5, обозначающее половину длины окружности, на 2:

Для вычисления длины окружности необходимо число Пи умножить на два и умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть следующим образом:

Для того чтобы посчитать площадь круга, необходимо умножить число Пи на радиус, взятый в квадрат (S = πR²). По условию задачи площадь круга равна Пи м кв. Это значит, что:

Из данного равенства можно выразить R

Зная длину радиуса, можно переходить к вычислению длины окружности (С):

C = 2πR = 2π x 1 = 2π

Ответ: Длина окружности равна 2π.

С целью вычисления длины окружности (С) используется приведенная ниже формула:

Ее составляющими является постоянное число Пи и радиус окружности (R), длину которой необходимо вычислить.

Если длина диаметра окружности является известной величиной, то его нужно умножить на постоянное число Пи, равное 3,14, для того чтобы найти длину этой окружности. Формула выглядит так:

В условии говорится, что диаметр окружности равен 15 см:

С = 3,14 * 15 = 47,1 cм.

Ответ: Длина окружности равна 47,1 см.

Для расчета длины окружности (С) нужно знать длину ее радиуса (R) или диаметра (d). Тогда могут быть использованы следующие формулы:

C = 2πR или C = πd

По условию задания d = 10 см, а π = 22/7. Тогда длина окружности будет равна:

C = πd = (22/7) * 10 = 220/7 ≈ 31,4 см.

В случае, если длина диаметра (d) или длина радиуса (R) окружности известны, то эти величины можно использовать для нахождения длины окружности. При этом следует воспользоваться одной из формул:

Эти величины также помогут вычислить площадь круга. Формулы выглядят следующим образом:

Нужно записать формулу расчета длины окружности, для того чтобы понять, существует ли взаимосвязь между этой величиной и диаметром окружности:

Очевидно, что длина окружности является результатом умножения числа Пи на длину ее диаметра.

Если длина окружности известна, то ее можно использовать для определения диаметра (d). Это можно сделать следующим образом:

Длину окружности (С) можно рассчитать через диаметр (d), если воспользоваться нижеприведенной формулой:

Это формула демонстрирует, что длина окружности больше длины ее диаметра в π раз. Именно отношение длины окружности к величине ее диаметра и является числом π.

Число π представляет собой константу, которая получается в результате деления длины окружности (С) на ее диаметр (d). В виде формулы это выглядит так:

Располагая информацией о том, что площадь круга равна произведению числа Пи и квадрата ее радиуса (S=πr²), можно через нее выразить радиус:

Избавляемся от квадратной степени:

Следующим шагом в решении задачи станет вычисление длины окружности, которая находится путем умножения на 2 числа Пи и радиуса окружности:

С=2πr= C=2π√(185/π) = 2√(185π) см.

На последнем этапе находим 30%. Принимаем всю длину окружности за 100%:

Тогда х можно найти следующим образом:

х=(30*2√(185π))/100 = 0,6√(185π) см.

Существует две формулы, которые предназначены для расчета длины окружности (С). Они отличаются друг от друга тем, что элементом одной из них является радиус (r), а другой – диаметр (D):

Для того чтобы понять, во сколько раз длина окружности превышает длину ее диаметра, нужно произвести деление этих величин:

В результате получается число Пи, которое является постоянным и имеет значение примерно 3,14.

Формула расчета длины окружности (С) через диаметр (D) выглядит так:

Исходя из условий задания, это равенство может быть записано в следующем виде:

Источник

Как рассчитать длину окружности и периметр круга?

Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.

Что такое окружность и где она встречается?

Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

Обозначения величин и формулы

До того как рассчитать длину окружности, потребуется договориться о том, какая буква что обозначает. Это удобно записать в таблице.

Величина	Обозначение
радиус	r
диаметр	d
длина окружности	l

Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:

l =2π * r.

Здесь и далее π берется округленным. Чаще всего в задачах используют значение 3,14. Но иногда нужна большая точность и тогда применяют такое число: 3,14159.

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:

l = π * d.

Как быть, если нужно вычислить периметр круга?

Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.

Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.

Примеры заданий

Задача первая

Условие. Узнать длину окружности, радиус которой равен 5 см.

Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).

Ответ: l = 31,4 см.

Задача вторая

Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.

Ответ: r = 200 мм.

Задача третья

Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.

Ответ: d = 18 см.

Задача четвертая

Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.

Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.

Ответ: l₁ = 18,84 см, l₂= 31,4 см.

Задача пятая

Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.

Ответ: Белка пробегает 6,28 м.

Источник

Периметр круга

Онлайн калькулятор

Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.

Ликбез: Круг — часть плоскости, лежащая внутри окружности.

Как посчитать периметр круга зная радиус

Чему равен периметр круга если

Формула

Пример

Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.

Как посчитать периметр круга зная диаметр

Чему равен периметр круга если

Каков периметр круга (L) если его диаметр d?

Формула

Пример

Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.

Как посчитать периметр круга зная его площадь

Чему равен периметр круга если

Каков периметр круга (L) если его площадь S?

Формула

Пример

Источник

Как рассчитать диаметр окружности, зная ее длину

Отправим материал на почту

Расчет диаметра круга легко произвести, зная другие параметры геометрической фигуры. Если информация о длине (P) доступна, искомое значение (D) быстро находится благодаря одной формуле D=P/π, где π — число Пи, бесконечное, кратко выражаемое как 3,14.

Определение

Диаметром круга принято считать размер прямой, соединяющей две любые точки на окружности и проходящей при этом через ее центр. Его также можно описать, как два радиуса, расположенные под углом 180° по отношению друг к другу.

Определение параметра вручную

Если значение величины кривой не выставлено, измерить искомый параметр можно непосредственно на чертеже.

Искомый показатель будет равняться длине отрезка между точками, появившимися на исходной замкнутой кривой как результат ее пересечения с выполненной в третьем пункте прямой линией.

Заключение

Быстро рассчитывать необходимые размеры геометрических тел можно с применением как формул, так и качественно составленных чертежей. Для этого важно всегда иметь под рукой базовый набор инструментов.

Источник

Рассчитать длину окружности по радиусу

Данный калькулятор позволяет быстро решать математические задачи, где необходимо найти длину окружности через радиус. Вам не придется самостоятельно вспоминать или искать формулы, лишь указать известные данные и получить готовый ответ!

Как пользоваться калькулятором?

Для получения точного расчета просто укажите известную длину радиуса, например, в сантиметрах в специальном окошке. После нажмите на кнопку «рассчитать. Внизу будет ответ, который легко скопировать.

Калькулятор рассчитывает с максимальным значением знаков после запятой, если вам необходимо 1-2 знака, просто округлите получившееся значение.

Пример расчета

Давайте попробуем произвести все подсчеты вручную, чтобы понять алгоритм работы калькулятора. Для вычисления длины окружности через радиус пригодится следующая математическая формула: P=2πr. При этом π = число пи, равное 3,14; а r = радиус окружности.

Пример задачи: найти длину окружности, если ее радиус равен 13 сантиметров.

Ответ на задачу: P = 2 х 3,14 х 13 = 81,64 см.

Источник

Как найти диаметр окружности

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.

Отметить точки пересечения прямой и окружности.

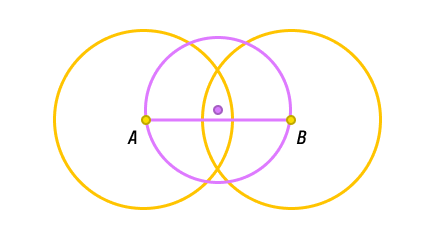
Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.

Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Источник

Как найти диаметр окружности через длину, площадь или радиус

Диаметр окружности онлайн калькулятор

Визуально выглядит так:

Выбираем вариант расчёта диаметра окружности

Введите длину окружности:

Введите площадь круга:

Введите радиус окружности:

Диаметр окружности (круга) равен :

Диаметр окружности (круга) равен :

Диаметр окружности (круга) равен :

Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Как рассчитать диаметр по длине,площади или радиусу окружности формула

Найти какой диаметр окружности можно в нашем онлайн калькуляторе даже не зная формул, просто введите цифры и получите результат

Источник

Как по окружности вычислить диаметр – Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.

формула и пояснения :: SYL.ru

Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?

Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.

Круг и окружность

Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.

А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.

После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.

Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.

Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.

Формула окружности через диаметр

Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.

Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.

Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.

Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).

Как вычислить диаметр: формула

На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?

Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.

Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.

Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.

Как вычислить диаметр окружности?

Для начала, давайте разберемся, что такое окружность и в чем ее отличие от круга. Возьмите ручку или карандаш красного цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее — и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

Как вычислить длину окружности. Формула длины окружности и круга

И хоть мы все учились в школе и вроде бы должны помнить длину окружности, но когда нам нужно для какого-то проекта или узнать сколько нужно метров для ограды круглого бассейна на даче вычислить длину окружности, мы не всегда можем вспомнить эту простую формулу.

Вычислить длину окружности можно при помощи одной из двух формул.

Вычисление длины круга через диаметр

C = πd
C – длина искомой окружности, d – диаметр данной окружности, π – всемирно известно число «пи», которое равно 3,14.

Пример: Допустим нам нужно поставить круглый забор на расстоянии 15 м вокруг бассейна у которого диаметр 10 м. Первым делом мы узнаем искомый нам диаметр нужной нам окружности по которой пройдет наш забор. Для этого к диаметр бассейна мы прибавляем расстояние на которое мы должны поставить забор с каждой стороны. Получаем d=10+15+15; d=40 м. Теперь подставляем наш диаметр в формулу и получаем, что длина искомой окружности получится С=3,14*40; С=125,6 м. Все теперь можно идти в строительный магазин и заказывать забор.

Вычисление длины круга через радиус

C = 2πr
C – длина искомой окружности, r – радиус данной окружности, π – постоянная величина которая всегда равна 3,14.

Пример: Предположим хозяйке для пирога нужно для пирога вырезать бумажную полоску. Радиус пирога 55 см. Подставляем наши данные в формулу и получаем, что длина окружности С = 55*3,14; С = 172,7 см.

Если Вы собираетесь производить свои вычисления на калькуляторе, то лучше всего, что бы там была кнопка π.

Sabibon — самое интересное в интернете

Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

Это интересно: как переводить градусы в радианы?

В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.

Это интересно: какой четырёхугольник называется квадратом?

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

Это интересно: что такое горизонтально, что означает слово горизонталь?

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Это интересно: формулировка и доказательство признаков параллелограмма.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Как рассчитать длину окружности

Как рассчитать длину окружности круга

1-й способ. Через диаметр
Длину окружности через длину диаметра можно рассчитать с помощью формулы:

Число является математической константой (постоянной), значение которой при вычислениях принято брать приближенное и равное 3,14.

Например, необходимо найти длину забора, которым нужно оградить бассейн с диаметром 25 метров. Забор должен располагаться на расстоянии 7 метров от края бассейна.
В таком случае находим диаметр забора, который будет ограждать бассейн:
(метров).
Находим длину забора:

2-й способ. Через радиус
Длину окружности через длину радиуса можно рассчитать с помощью следующей формулы:

Такую формулу легко получить, зная формулу через диаметр (и наоборот). Для этого нужно только использовать тот факт, что диаметр равен двум радиусам.

Например, необходимо найти размер ленты, которой нужно обшить шляпку радиуса 17 см. В таком случае, воспользуемся формулой:

Как найти диаметр окружности

Перед тем, как найти диаметр окружности, нужно изучить само определение диаметра. Это отрезок, который проходит через ее центр и и объединяет между собой две удаленные на ней точки.

В прикладных задачах часто необходимо найти диаметр шара или круга.

Диаметр окружности определяют по ее площади, длине или радиусу круга. Диаметр шара можно найти по объему, радиусу или площади поверхности.

Как вычислить диаметр окружности:

Если диаметр необходимо найти, зная радиус окружности или шара, то следует применить следующую основную формулу:

D = 2 * R,
где D – диаметр фигуры,
R – расстояние от центра до любой точки на ней.

Пример: радиус равен 5 см. Найти диаметр данной окружности. Для этого: 5 см*2=10 см.
Ответ: 10 сантиметров.

Как определить диаметр окружности через ее длину?

Здесь надо воспользоваться формулой для вычисления длины окружности:

L = 2 π * R,
где L – длина данной окружности,
2 — константа,
π = 3,14,
R – радиус.

Известно, что диаметр – радиус умноженный на два, тогда вышеуказанную формулу можно записать в следующем виде:
L = π * D,
где D – диаметр.

Как узнать диаметр окружности?

Из вышеприведенной формулы выразить диаметр:

и подставить в нее величины данные в задаче, вычислив уравнение с одним неизвестным.

Пример: Определить диаметр окружности, если ее длина составляет 6 метров. Решение: 6/3,14=1,91.
Ответ: диаметр равен 1,91 метрам.

Также самое для круга, если дана его площадь. Для этого нужно в решении использовать следующую формулу:

D = 2 * √(S / π)
где S – площадь окружности.

Если известен объем шара, то диаметр его можно вычислить по формуле:

D = 2* 3 √((3 V) /(4 π))
где V – объем шара.

Источник