Как зашифровать слово цифрами
Как зашифровать слово цифрами
ФОЦПМРЬОЯКЦА: разбираемся в шифрах
Любовь Карась
Тарабарщина, абракадабра, затейное письмо — зашифрованные сообщения называли по-разному. Это был надежный способ передавать тайную информацию. Раньше умение дешифровать загадочные письма приравнивалось к сверхспособности, ведь нужно было обладать логическим, критическим и креативным мышлением. Вместе с экспертом Музея криптографии, который откроется в декабре этого года, рассказываем о популярных шифрах, а также о том, как их разгадать. Можете проверить себя!
Анастасия Ашаева
Кандидат исторических наук, старший научный сотрудник Музея криптографии
Атбаш
Этот шифр считается одним из самых древних в истории криптографии. Он появился примерно две с половиной тысячи лет назад на Ближнем Востоке. Чаще всего этот шифр можно встретить в религиозных текстах (кумранские рукописи, Ветхий Завет), где с его помощью скрывали, например, названия городов или имена собственные. Принцип шифрования очень прост: нужно написать алфавит в обратном порядке, так, чтобы под буквой «А» оказалась буква «Я», под буквой «Б» — буква «Ю» и так далее, а потом каждую букву сообщения, которое следует зашифровать, заменить на букву из алфавита, написанного в обратном порядке.
Такой незатейливый, но действенный способ шифрования и есть атбаш, то есть «алеф», «тав», «бет» и «шин» — первая, последняя, вторая и предпоследняя буквы еврейского алфавита.
Интересный факт: самое известное упоминание шифра атбаш — в романе Дэна Брауна «Код да Винчи», где главные герои дешифруют сообщение, зашифрованное с помощью этого шифра, что позволяет им приблизиться к разгадке тайны святого Грааля.
Квадрат Полибия
Интересный факт: изначально квадрат Полибия выполнял две функции: с его помощью можно было как зашифровать сообщение, так и передать его на дальнее расстояние посредством оптического телеграфа. Делалось это при помощи группы факелов: сначала поднимались факелы слева, количество которых указывало номер строки, а потом — факелы справа, указывающие номер столбца. Для получения и расшифрования такого сообщения адресату нужно было иметь точно такой же квадрат, а также зорко следить за количеством поднятых факелов.
Проверьте себя: «Телеграфируем» фразу «ОЧШОУеЗЗОУК» (34 51 52 34 43 21 23 23 34 43 26)
Шифр Цезаря
Известный шифр Античности получил имя самого известного политического деятеля и полководца Древнего мира неспроста. Юлий Цезарь мог одновременно не только писать, читать, диктовать и слушать, но и шифровать. Своим потомкам в наследство он оставил великую Римскую империю и шифр, которым, по свидетельствам античных авторов, императоры пользовались почти до самого падения империи.
В шифре, который был придуман Цезарем, для зашифрования нужно заменять каждую букву слова на букву, которая следует за ней третьей по счету: например, букву «А» мы заменим на букву «Г», а букву «Б» — на букву на «Д» и т. д. В целом сдвигать буквы можно на любое количество позиций вправо, и именно знание о том, на сколько букв вправо был сдвиг, и позволит расшифровать сообщение.
Интересный факт: шифр Цезаря лег в основу многих более сложных шифров и использовался вплоть до начала XX века, когда были изобретены первые шифровальные машины. И по сей день этот шифр считается наиболее важным и значимым в истории криптографии.
Проверьте себя: «ТУЛЫЗОЦЕЛЖЗОТСДЗЖЛО» — так выглядит одно из известных выражений, приписываемых Юлию Цезарю, зашифрованное при помощи шифра Цезаря со сдвигом на три позиции вправо. Попробуй расшифровать!
Опыт всему учитель
Пришел, увидел, победил
Русская литорея
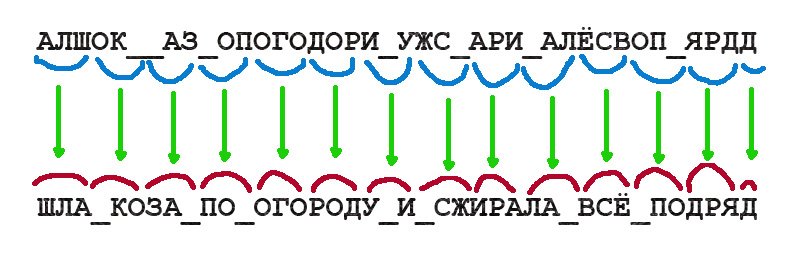
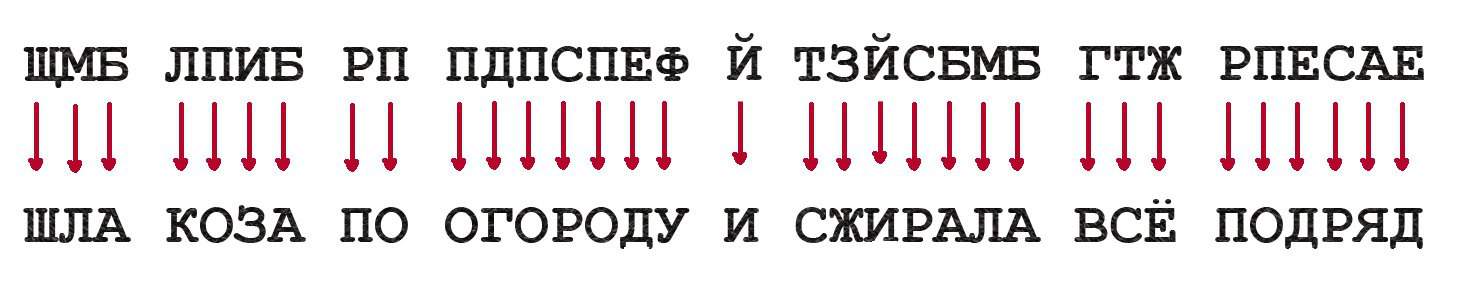
В средневековой Руси тоже любили шифровать. Зачастую шифры использовались в качестве украшения в литературных произведениях. Авторы шифровали свое имя и даже целые главы текста, используя тайнопись как литературный прием, который позволял выделить такой труд из множества других. Наиболее распространенным шифром в это время в России была литорея (от латинского слова littera — «буква»). Шифр предполагал замену согласных букв на согласные буквы по определенному правилу.
Под первыми десятью согласными буквами (за исключением «Й»), идущими по порядку, записывались другие десять согласных букв, но в порядке, противоположном тому, который использовался в верхней строке. Таким образом, под буквой «Б» оказывалась буква «Щ», а под буквой «В» — буква «Ш» и т. д.
Интересный факт: известное всем слово «тарабарщина» в веках означало не что иное, как шифр литорея, и употреблялось в качестве синонима. Одна из историй возникновения этого слова гласит, что для сохранения тайны передаваемого сообщения его зашифровывали, но не писали на бумаге, а давали гонцам заучивать наизусть. Гонцы доставляли сообщение адресату в виде устного послания, а так как произнести зашифрованный текст и понять его порой было непросто, он и получил название «тарабарщина».
Век живи — век учись
Без труда не выловишь и рыбку из пруда
Не плюй в колодец, пригодится воды напиться
Шифр Виженера
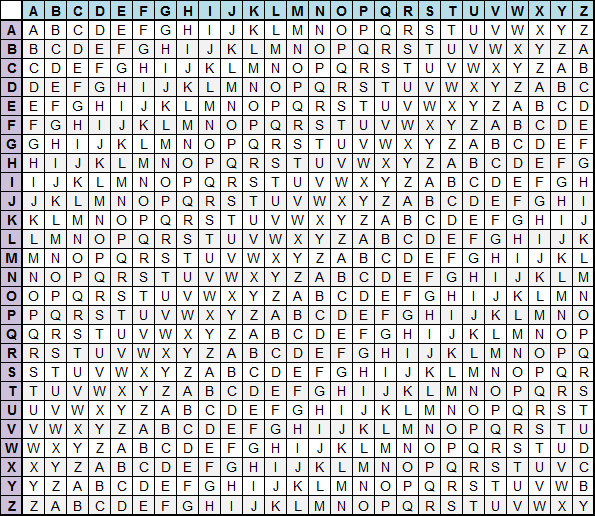
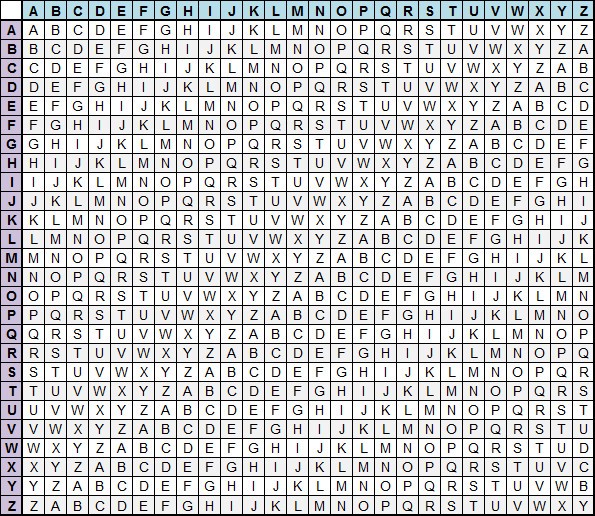
Новую эру в криптографии знаменует открытие полиалфавитного шифра, известного также как шифр Виженера. Описанный в 1586 году французским дипломатом Блезом де Виженером, шифр долго оставался нераскрытым, пережив множество усложнений и модификаций и став своеобразным мостиком для изобретения первых механических шифровальных машин. Для шифрования использовалась специальная таблица, в которой количество строк и столбцов соответствовало количеству букв в алфавите. Таким образом, каждая буква в исходном тексте сдвигается по алфавиту на разное количество символов и количество сдвигов каждой буквы задается специальным ключом (ключевым словом).
Для простоты использования слово (или фраза,) которое нужно было зашифровать, записывалось в строку, а под ней писалось ключевое слово и повторялось несколько раз подряд, чтобы под каждой буквой исходного текста оказалась буква ключевого слова. Далее мы берем букву из сообщения и букву из ключевого слова под ней и обращаемся к таблице. Буква, которая будет на пересечении этих двух букв в таблице, и станет первой буквой криптограммы.
Интересный факт: Несмотря на то что шифр носит имя Виженера, сам Виженер его не изобретал. Шифр был придуман в 1466 году итальянским гуманистом, ученым и архитектором Леоном Баттистой Альберти. Вклад в его развитие внесли современники Альберти, среди которых — немецкий гуманист и аббат Иоганн Тритемий и итальянский ученый Джованни Баттиста Беллазо. Виженер же просто описал все известные ему способы шифрования, а в XIX веке за шифром прочно закрепилось имя Виженера, под которым он известен и по сей день.
Проверьте себя: «ЧФЩЪОВН ЙЪЯФОН» — так бы мог выглядеть призыв к атаке, зашифрованный при помощи таблицы Виженера с использованием ключевого слова «мел».
Элементарные шифры на понятном языке
Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.
Прежде всего, разберемся в терминологии.
Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.
Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.
Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.
Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.
Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.
Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.
Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.
Шифр Атбаша
Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.
Например, есть у нас алфавит, который полностью соответствует обычной латинице.
Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:
И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра
Исходное сообщение: I love habr
Зашифрованное: r olev szyi
Шифр Цезаря
Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.
Опять же, для наглядности, возьмем латиницу
И теперь сместим вправо или влево каждую букву на ключевое число значений.
Например, ключ у нас будет 4 и смещение вправо.
Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v
Пробуем написать сообщение:
Шифруем его и получаем следующий несвязный текст:
Шифр Вернама (XOR-шифр)
Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).
Исходный алфавит — все та же латиница.
Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.
Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.
XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.
Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.
Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ
сообщение: LONDON
ключ: SYSTEM
Переведем их в бинарный код и выполним XOR:
В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:
С виду — совершенно несвязный набор чисел, но мы-то знаем.
Шифр кодового слова
Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.
Например, возьмем для разнообразия, кириллический алфавит.
Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».
Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.
И теперь запишем любое сообщение и зашифруем его.
Получим в итоге следующий нечитаемый бред:
Шифр Плейфера
Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.
Пусть кодовое слово у нас будет «HELLO».
Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.
Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».
Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.
Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.
Шифрование выполняется по нескольким несложным правилам:
1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.
Например, EH становится LE.
2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.
Например, если бы у нас была биграмма LX, то она стала бы DL.
3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.
Например, биграмма RA.
По этим правилам, шифруем все сообщение.
Если убрать пробелы, то получим следующее зашифрованное сообщение:
Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.
ШИФРОВАНИЕ ЦИФРАМИ



При шифровании методом подстановки, буквы исходного текста могут заменяться на геометрические фигуры, фигурки людей, животных, любые рисунки, символы, буквы или цифры (группы).
КАЖДАЯ БУКВА КОДИРУЕТСЯ ТОЛЬКО ОДНИМ ЧИСЛОМ
По этой таблице закодирована шифровка из детской книжки-раскраски. Современная алфавитная позиционная нумерация аналогична числовому соответствию литеры в славянской азбуке. Это простая таблица. Здесь числа, используемые для кодирования, расположены по порядку.
Здесь числа (двузначные цифровые группы) набраны в лотерейном порядке по принципу случайных чисел.
КАЖДАЯ БУКВА КОДИРУЕТСЯ ДВУМЯ ГРУППАМИ
Общее количество чисел (цифровых групп), используемых для кодирования, в 2 раза больше чем букв.
ИСПОЛЬЗОВАНИЕ ДЛЯ ЗАМЕНЫ КАЖДОЙ БУКВЫ НЕСКОЛЬКИХ ГРУПП
В процессе шифрования для замены каждой буквы могут использоваться 3, 4 и более групп. Соответственно общее количество групп, используемых для шифрования, может быть в 3, 4 и n раз больше чем букв в алфавите.
КОДИРОВАНИЕ С УСЛОЖНЕНИЕМ.
В отличие от приложения № 30 все числа, используемые здесь для кодирования букв, взяты из таблицы умножения. Слово «ШАЛАШ» закодированное по кодовой таблице, представленной в приложении № 33, будет иметь такой вид: 10 24 40 24 10.
Усложняя с помощью таблицы умножения, заменяем код буквы на множители: вместо «10» пишем «25» или «52» (2´5 = 5´2 = 10), «24» заменяем на «38», «83», «46» или «64» (3´8 = 8´3 = 4´6 = 6´4 = 24) и т. д. После усложнения шифровка будет выглядеть так: 25 38 85 46 52. Таким образом для кодирования каждой буквы будет использоваться не одно число, а несколько (2-4), что сделает шифр более надежным, т. к. в зашифрованном тексте одни и те же числа (группы) будут повторяться реже.
Даже если Вы потеряете такую таблицу, или ее похитят, подсмотрят, скопируют, злоумышленники не смогут этим воспользоваться (расшифровать) т.к. в криптограмме цифровых групп из кодовой таблицы не будет, а будут группы, состоящие из множителей.
Чтобы не привлекать внимание посторонних, шифрограмма может быть замаскирована под арифметические действия первоклассника и записана так:
2´5 = 10, 3´8 = 24, 8´5 = 40, 4´6 = 24, 5´2 = I0
Сообщение можно передавать короткими частями.
ДЛЯ ЗАМЕНЫ КАЖДОЙ БУКВЫ ИСПОЛЬЗУЕТСЯ РАЗНОЕ КОЛИЧЕСТВО ГРУПП
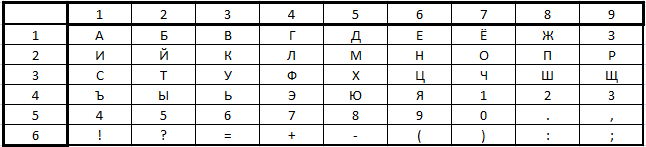
Рассмотрим систему шифрования в виде таблицы размером 10‰10 (размеры могут быть другими). Пронумеруем строки и столбцы. Десятые строку и столбец обозначим нулём (нумерацию можно начать не с 1, а с 0). Нумерация может быть буквенной. Причём для нумерации строк и столбцов могут использоваться не одни и те же, а разные буквы. Каждая клетка имеет координаты, состоящие из двух цифр или букв – номер строки и номер столбца. Заполним ячейки таблицы буквами алфавита, необходимыми знаками препинания, цифрами. При этом 100 ячеек распределим пропорционально, в зависимости от частоты употребления букв в русском языке. Несколько клеток оставим пустыми. Пустышки при необходимости будем применять вместо пробелов, для обозначения красной строки, для доукомплектования последних групп (в случае перегруппировки) и в качестве резерва.
В простейшем варианте буквы вписываются в таблицу в алфавитном порядке, а цифры в возрастающей последовательности (такое расположение символов не трудно запомнить). Причём, часто встречающиеся буквы повторяются необходимое количество раз: так буква О займёт 8-9 клеток, буква Е займёт 7-8 клеток, буква А повторяется 6-7 раз, букву И запишем 5-6 раз и т.д. Нумерацию строк и столбцов можно сделать в обратном или случайном порядке.
В усложнённом варианте сначала вписывается какой-нибудь заученный текст (например, стихотворение), затем дописываются буквы алфавита, не вошедшие в этот текст. Сначала вписываются какие-либо запомнившиеся цифры (например, 1945 – год окончания второй мировой войны), потом остальные. Таким образом, расположение знаков в таблице будет условно-случайным, что повышает стойкость шифра. Применяются разные правила заполнения таблицы в удобном для запоминания порядке. В нашем примере в таблицу (приложение № 34) в начале записана заученная фраза, за ней – запомнившиеся цифры, потом остальные буквы алфавита, далее следуют знаки препинания и оставшиеся цифры, и, наконец, дописаны необходимое количество раз часто встречающиеся буквы. Нумерация строк и столбцов имеет два варианта (цифровой и буквенный).
В процессе шифрования буква исходного текста отыскивается в таблице и заменяется на двузначную цифровую группу (координаты), в которой одна цифра является номером строки, а другая – номером столбца.
Зашифруем текст (ЛУЧШЕ БОЛЬШОЙ ДОСТАТОК, ЧЕМ МАЛЕНЬКИЙ НЕДОСТАТОК.) и получим криптограмму ( 17 45 49 40 10 37 13 88 18 40 24 43 39 95 15 12 29 23 96 11 57 49 21 44 89 68 17 77 19 18 87 16 43 80 78 76 97 05 25 69 08 98 11 50 ). В полученной криптограмме, не смотря на короткий открытый текст, просматриваются повторяющиеся (одинаковые) двузначные группы. Если шифровку перегруппировать в группы по 3, 4 или 5 символов, повторы одинаковых двузначных групп будут незаметны.
Если применить буквенную нумерацию строк и столбцов, шифрограмма будет иметь другой вид: ЛЖ ОД ОИ ОК ЛК НЖ ЛВ ТЗ ЛЗ ОК МГ ОВ НИ УД ЛД ЛБ МИ МВ УЕ ЛА ПЖ ОИ МА ОГ ТИ РЗ ЛЖ СЖ ЛИ ЛЗ ТЖ ЛЕ ОВ ТК СЗ СЕ УЖ ФД МД РИ ФЗ УЗ ЛА ПК. Для усложнения можно в каждой второй группе шифрограммы символы записывать в обратном порядке – сначала номер столбца, а затем номер строки. Или комбинировать – чередовать цифровые и буквенные группы.
Рассматриваемая таблица отличается от постолбцовой таблицы замены, показанной в приложении № 32, тем, что кроме случайного соответствия символ–двузначная группа, мы имеем неодинаковое (приблизительно пропорциональное частоте употребления) количество заменяющих групп для разных букв, что уменьшает проявление в шифрограмме закономерностей и характеристик исходного текста.
ШИФРОБЛОКНОТ ИЗГОТОВЛЕНИЕ ШИФРОБЛОКНОТА
Для шифрования используйте 1000 групп, по три цифры в каждой (трехзначные числа): 000, 001, 002, 003 и так далее до 999.
Для простоты распределите трёхзначные группы поровну. 1000 : 36 = 27 и 28 в остатке. Для шифрования каждой буквы и знаков препинания используйте по 27 групп. Остальные 28 оставьте в резерве. Для резерва выделите отдельную страницу.
Достаньте из коробки очередной, третий, номерок. Запишите следующее число в блокнот, например, 952. И т.д. пока на странице с буквой “А” ни будет записано 27 групп.
323 162 952 338 566 532 959 379 005 837 832 582 035 818 460 615 907 464 814 931 564 690 305 405
336 259 179 286 177 059 236 790 971 113 504 390 910 331 458 422 856 496 025 370 217 232 794 598 724 345 486
Аналогично набираете и вписываете числа (трёхзначные цифровые группы) для других букв и знаков препинания. Оставшиеся 28 групп запишите в резерв.
Шифроблокнот и дешифрант к нему показаны в приложении № 35.
ШИФРОВАНИЕ ТЕКСТА
Аналогично шифруйте остальные буквы текста (в приведённом примере их нет). Получилась шифрограмма: 336 323 259 162. Для замены каждой буквы можно использовать любые из 27 групп, предназначенных для данной буквы, в любом порядке, не допуская повторного использования одной и той же группы.
РАСШИФРОВАНИЕ
Для расшифрования криптограммы найдите в дешифранте порядковый № 336. Напротив него стоит буква
Получится:
336 323 259 162
ПРАВИЛА РАБОТЫ
Работа с конфиденциальной информацией и СРШ-ДРК должна проводиться в отсутствии посторонних. При шифровании запрещается повторное использование одной и той же группы. Если текст большой и блокнот не позволяет зашифровать весь текст без повторного использования групп, разбейте его на части и передавайте по частям, как отдельные шифрограммы.
Уничтожайте испорченные листы и черновики, а также утратившие значение шифрограммы и секретные тексты.
Можно разбить алфавит попарно и для замены буквы «А» использовать группы, предназначенные для буквы «Б». Для замены буквы «Б» применять группы, предназначенные для буквы «А», и так далее.
Ключ менять по специальному секретному графику (расписанию смены ключа).
10 популярных кодов и шифров
Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.
В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.
Стандартные шифры
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».
Попробуйте расшифровать сообщение:
Сумели? Напишите в комментариях, что у вас получилось.
Шифр транспонирования
В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.
Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:
Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:
Азбука Морзе
В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов: 
Сможете расшифровать сообщение, используя картинку?
Шифр Цезаря
Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.
А здесь использован шифр Цезаря с шагом 5:
Моноалфавитная замена
Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.
Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».
Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.
Шифр Виженера
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.
В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.
Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.
Попробуйте расшифровать эту фразу самостоятельно:
Подсказка длина кодового слова — 4.
Шифр Энигмы
Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.
Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.
Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.
Цифровые шифры
В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.
Двоичный код
Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.
Расшифруйте следующее сообщение, в котором использована кириллица:
Шифр A1Z26
Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.
Попробуйте определить, что здесь написано:
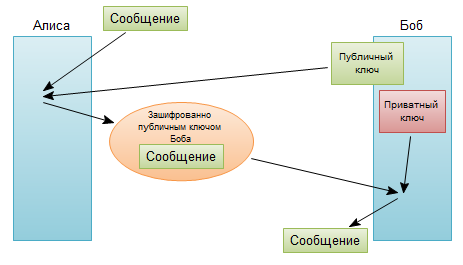
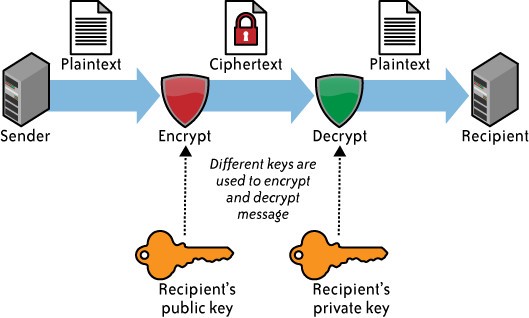
Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.
Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.
Как расшифровать код или шифр?
Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:
Расшифруй слова по цифрам
1) Алфавит разбивается на группы с равным числом букв, затем каждой группе присваивается свой номер. Так формируется первая цифра для шифровки символа. Вторая цифра – это порядковый номер буквы в группе.
Таблица не обязательно должна выглядеть таким образом. Количество групп может быть другим. Также буквы из алфавита могут идти в таблице не по порядку.
Зашифруем таким способом слово «цифра»
Зашифрованный текст: 63 31 61 51 11
Возможно много вариаций этого вида шифра. Например, алфавит разбивается на 5 групп, а каждая буква будет изображаться дробью таким образом, что в числителе будет номер ее группы, а в знаменателе – порядковый номер в группе. Еще один вариант, как я уже говорил, буквы могут идти не по порядку (например, ажмтшю бзнущя виофъ гйпхы дкрць елсчэ).
2) Цифровая таблица.
Зашифруем с помощью этой таблицы слово «наука».
Каждый символ будет шифроваться опять двумя цифрами, при чем первой может быть как номер столбца, так и номер строки. То есть буква К может быть зашифрована, как 32 или 23.
Зашифрованный текст: 62 11 33 32 11
Здесь первой цифрой записан номер столбца, второй – номер строки.
3)Шифрование с заменой каждой буквы ее номером в алфавите. Очень простой вид шифра. Его, думаю, можно тоже отнести к цифровым. Но между тем, он часто применяется в различных вариациях и комбинациях с другими видами шифров. Про некоторые комбинации шифров расскажу чуть позже.
Вариация этого шифра: буквы в алфавите отсчитываются не с начала, а с конца. То есть порядковым номер буквы «А» будет 33, «Б» – 32 и так далее.
Дата добавления: 2014-12-24 ; Просмотров: 9111 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.
Ниже калькулятор, который позволяет зашифровать/расшифровать текст, используя шифр A1Z26. Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.
Все буквы приводятся к нижнему регистру, зашифровывается/расшифровывается русский алфавит, все не-алфавитные символы не преобразуются. При расшифровке учтите, что числа (от 1 до 33) должны быть отделены друг от друга (чертой, пробелом или неважно чем). Для зашифровки/расшифровки с использованием английского алфавита переключите язык сайта на английский.
Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.
Прежде всего, разберемся в терминологии.
Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.
Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.
Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.
Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.
Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.
Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.
Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.
Шифр Атбаша
Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.
Например, есть у нас алфавит, который полностью соответствует обычной латинице.
Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:
И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра
Исходное сообщение: I love habr
Зашифрованное: r olev szyi
Шифр Цезаря
Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.
Опять же, для наглядности, возьмем латиницу
И теперь сместим вправо или влево каждую букву на ключевое число значений.
Например, ключ у нас будет 4 и смещение вправо.
Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v
Пробуем написать сообщение:
Шифруем его и получаем следующий несвязный текст:
Шифр Вернама (XOR-шифр)
Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).
Исходный алфавит — все та же латиница.
Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.
Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.
XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.
Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.
Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ
сообщение: LONDON
ключ: SYSTEM
Переведем их в бинарный код и выполним XOR:
В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:
С виду — совершенно несвязный набор чисел, но мы-то знаем.
Шифр кодового слова
Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.
Например, возьмем для разнообразия, кириллический алфавит.
Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».
Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.
И теперь запишем любое сообщение и зашифруем его.
Получим в итоге следующий нечитаемый бред:
Шифр Плейфера
Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.
Пусть кодовое слово у нас будет «HELLO».
Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.
Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».
Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.
Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.
Шифрование выполняется по нескольким несложным правилам:
1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.
Например, EH становится LE.
2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.
Например, если бы у нас была биграмма LX, то она стала бы DL.
3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.
Например, биграмма RA.
По этим правилам, шифруем все сообщение.
Если убрать пробелы, то получим следующее зашифрованное сообщение:
Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.
Популярные коды и шифры.
В рубрике “Информационная безопасность” мы разбирали общие вопросы о криптографии и методах шифрования. В этой статье мы рассмотрим самые популярные коды и шифры.
В мире существует множество шифров и кодов для засекречивания различных посланий. Вопреки распространенному мнению, код и шифр — это не одно и то же. В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения.
1. Шифр Цезаря
Шифр Цезаря так называется, потому что его использовал сам Юлий Цезарь. Шифр Цезаря — это не один шифр, а целых двадцать шесть, использующих один и тот же принцип. Например, шифр ROT1 относится к шифру Цезаря.
Получателю нужно сказать, какой из шифров используется. Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров.
Шифр Цезаря очень простой и быстрый, но он является шифром простой одинарной перестановки и поэтому легко взламывается.
2. Азбука Морзе
Азбука является средством обмена информации и ее основная задача – сделать сообщения более простыми и понятными для передачи. В системе Морзе каждая буква, цифра и знак препинания имеют свой код, составленный из группы тире и точек. При передаче сообщения с помощью телеграфа тире и точки означают длинные и короткие сигналы. Пример:
3. Стеганография
Стеганография старше кодирования и шифрования. Это искусство появилось очень давно. Оно буквально означает «скрытое письмо» или «тайнопись». Хоть стеганография не совсем соответствует определениям кода или шифра, но она предназначена для сокрытия информации от чужих глаз. Про стеганографию можно почитать в нашей отдельной статье.
4. ROT1
Данный шифр известен всем с детства. Каждая буква шифра заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д.
«ROT1» значит «ROTate 1 letter forward through the alphabet» («сдвиньте алфавит на одну букву вперед»).
5. Моноалфавитная замена
Описанные выше ROT1 и азбука Морзе являются представителями шрифтов моноалфавитной замены. Приставка «моно» означает, что при шифровании каждая буква изначального сообщения заменяется другой буквой или кодом из единственного алфавита шифрования.
Дешифрование шифров простой замены не составляет труда, и в этом их главный недостаток. Разгадываются они простым перебором или частотным анализом.
6. Транспозиция
В транспозирующих шифрах буквы переставляются по заранее определенному правилу. Например, если каждое слово пишется задом наперед, то из «all the better to see you with» получается «lla eht retteb ot ees joy htiw».
В Гражданскую войну в США и в Первую мировую его использовали для передачи сообщений.
7. Шифр Виженера
Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом.
Данный шифр на порядок более устойчив к взлому, чем моноалфавитные, хотя представляет собой шифр простой замены текста. Пример:
Давайте зашифруем слово “Пароль” с помощью данного шифра. Ключевое слово будем использовать “Код”. Нарисуем таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Фраза: | п | а | р | о | л | ь |
| Ключ | к | о | д | к | о | д |
Берем первые буквы ключа и нашего слова и скрещиваем между собой с помощью таблицы Виженера и получается буква “ъ” и идем далее. Остальное попробуйте самостоятельно и напишите ответ в комментариях
8. Настоящие коды
В настоящих кодах каждое слово заменяется на другое. Расшифровывается такое послание с помощью кодовой книги, где записано соответствие всех настоящих слов кодовым, прямо как в словаре.
Многие страны использовали коды, периодически их меняя, чтобы защититься от частотного анализа. Но есть минус: если кодовая книга будет украдена, то с ее помощью больше будет невозможно что-либо зашифровать, и придется придумывать новый код, что требует огромных усилий и затрат времени.
9. Шифр Энигмы
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.
Существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.
10. Шифр Гронсфельда
Шифр Гронсфельда — это модификация шифра Цезаря. Данный способ является значительно более стойким к взлому и заключается в том, что каждый символ кодируемой информации шифруется при помощи одного из разных алфавитов, которые циклически повторяются. Можно сказать, что это многомерное применение простейшего шифра замены.
11. Шифрование методом публичного ключа
Суть данного шифра заключается, как правило, в наличии двух ключей, один из которых передается публично, а второй является секретным (приватным). Открытый ключ используется для шифровки сообщения, а секретный — для дешифровки.
В роли открытого ключа чаще всего выступает очень большое число, у которого существует только два делителя, не считая единицы и самого числа. Вместе эти два делителя образуют секретный ключ.
Шифр цифры вместо букв
Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.
Ниже калькулятор, который позволяет зашифровать/расшифровать текст, используя шифр A1Z26. Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.
Все буквы приводятся к нижнему регистру, зашифровывается/расшифровывается русский алфавит, все не-алфавитные символы не преобразуются. При расшифровке учтите, что числа (от 1 до 33) должны быть отделены друг от друга (чертой, пробелом или неважно чем). Для зашифровки/расшифровки с использованием английского алфавита переключите язык сайта на английский.
Шифр Цезаря– сдвиг по алфавиту на N букв вперед (В классическом варианте сдвиг на 3 буквы вперёд)
Шифр Гронфельда — шифр замены, использующий число в качестве ключа для текста.
Под буквами письма, излагаемого шифром, подписываются по порядку цифры секретного числа одна за другою так, чтобы под каждой буквой стояла цифра; затем в письме вместо обыкновенных букв ставят другие буквы, отстоящие в общепринятой азбуке от первых на столько букв, сколько единиц в числе, обозначенном соответствующей цифрой.
Древней Греции (П в. до н. э.) был известен шифр, называемый «квадрат Полибия». Это устройство представляло собой квадрат 5×5, столбцы и строки которого нумеровали цифрами от 1 до 5. В каждую клетку этого квадрата записывалась одна буква. (В греческом варианте одна клетка оставалась пустой, в латинском – в одну клетку помещали две буквы i и j.) В результате каждой букве отвечала пара чисел и шифрованное сообщение превращалось в последовательность пар чисел.
Например: 13 34 22 24 44 34 15 42 22 34 43 45 32
(Cogito ergo sum)
Это сообщение записано при использовании латинского варианта «квадрата Полибия «, в котором буквы расположены в алфавитном порядке.
Этот шифр удобнее всего представлять себе как шифр Цезаря с переменной величиной сдвига. Чтобы знать, на сколько сдвигать очередную букву открытого текста, заранее договариваются о способе запоминания сдвигов. Сам Виженер предлагал запоминать ключевое слово, величину сдвига. Существует алгоритм шифрования по таблице Виженера:
Дешифровка осуществляется по обратному алгоритму, с учётом того, что 5-я строка – разность 2-й и 4-й строки. Если число 2-й строки меньше числа 4-й строки, считаем так: 33 + число 2-й строки – число 4-й строки.
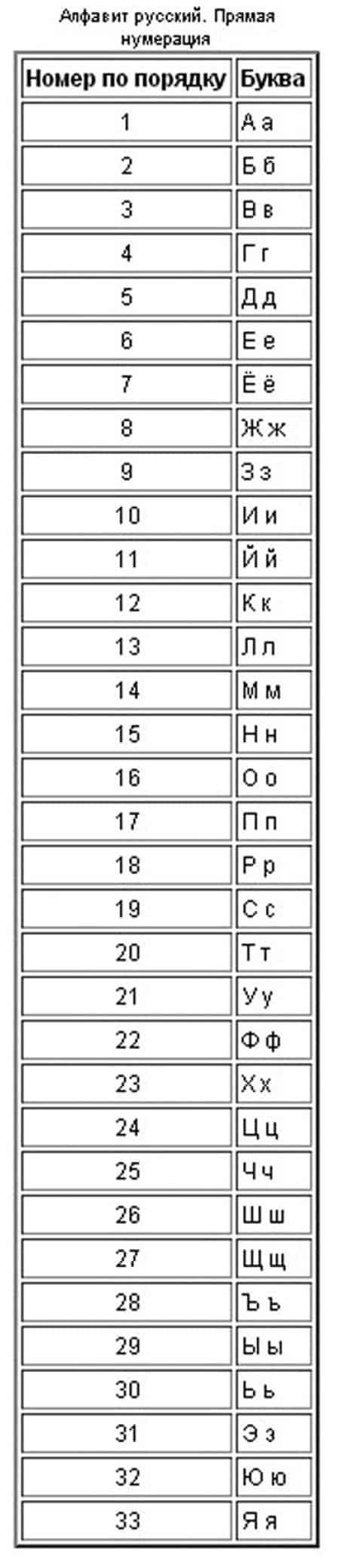
А-1 Б-2 В-3 Г-4 Д-5 Е-6 Ё-7 Ж-8 З-9 И-10 Й-11 К-12 Л-13 М-14 Н-15 О-16 П-17 Р- 18 С-19 Т- 20 У-21 Ф-22 Х-23 Ц- 24 Ч-25 Ш- 26 Щ-27 Ъ- 28 Ы-29 Ь-30 Э-31 Ю-32 Я-33
Шифр Атбаш – Шифр простой замены, использованный для еврейского алфавита и получивший оттуда свое название. Шифрование происходит заменой первой буквы алфавита на последнюю, второй на предпоследнюю.
Для английского алфавита:
Исходный алфавит: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Алфавит замены : Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Для русского алфавита:
Исходный алфавит: А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Алфавит замены: Я Ю Э Ъ Ы Ь Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Ё Е Д Г В Б А
Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.
Прежде всего, разберемся в терминологии.
Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.
Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.
Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.
Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.
Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.
Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.
Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.
Шифр Атбаша
Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.
Например, есть у нас алфавит, который полностью соответствует обычной латинице.
Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:
И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра
Исходное сообщение: I love habr
Зашифрованное: r olev szyi
Шифр Цезаря
Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.
Опять же, для наглядности, возьмем латиницу
И теперь сместим вправо или влево каждую букву на ключевое число значений.
Например, ключ у нас будет 4 и смещение вправо.
Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v
Пробуем написать сообщение:
Шифруем его и получаем следующий несвязный текст:
Шифр Вернама (XOR-шифр)
Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).
Исходный алфавит — все та же латиница.
Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.
Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.
XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.
Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.
Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ
сообщение: LONDON
ключ: SYSTEM
Переведем их в бинарный код и выполним XOR:
В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:
С виду — совершенно несвязный набор чисел, но мы-то знаем.
Шифр кодового слова
Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.
Например, возьмем для разнообразия, кириллический алфавит.
Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».
Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.
И теперь запишем любое сообщение и зашифруем его.
Получим в итоге следующий нечитаемый бред:
Шифр Плейфера
Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.
Пусть кодовое слово у нас будет «HELLO».
Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.
Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».
Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.
Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.
Шифрование выполняется по нескольким несложным правилам:
1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.
Например, EH становится LE.
2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.
Например, если бы у нас была биграмма LX, то она стала бы DL.
3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.
Например, биграмма RA.
По этим правилам, шифруем все сообщение.
Если убрать пробелы, то получим следующее зашифрованное сообщение:
Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.
Цифровые шифры
1) Алфавит разбивается на группы с равным числом букв, затем каждой группе присваивается свой номер. Так формируется первая цифра для шифровки символа. Вторая цифра – это порядковый номер буквы в группе.
Таблица не обязательно должна выглядеть таким образом. Количество групп может быть другим. Также буквы из алфавита могут идти в таблице не по порядку.
Зашифруем таким способом слово «цифра»
Зашифрованный текст: 63 31 61 51 11
Возможно много вариаций этого вида шифра. Например, алфавит разбивается на 5 групп, а каждая буква будет изображаться дробью таким образом, что в числителе будет номер ее группы, а в знаменателе – порядковый номер в группе. Еще один вариант, как я уже говорил, буквы могут идти не по порядку (например, ажмтшю бзнущя виофъ гйпхы дкрць елсчэ).
2) Цифровая таблица.
Зашифруем с помощью этой таблицы слово «наука».
Каждый символ будет шифроваться опять двумя цифрами, при чем первой может быть как номер столбца, так и номер строки. То есть буква К может быть зашифрована, как 32 или 23.
Зашифрованный текст: 62 11 33 32 11
Здесь первой цифрой записан номер столбца, второй – номер строки.
3)Шифрование с заменой каждой буквы ее номером в алфавите. Очень простой вид шифра. Его, думаю, можно тоже отнести к цифровым. Но между тем, он часто применяется в различных вариациях и комбинациях с другими видами шифров. Про некоторые комбинации шифров расскажу чуть позже.
Вариация этого шифра: буквы в алфавите отсчитываются не с начала, а с конца. То есть порядковым номер буквы «А» будет 33, «Б» – 32 и так далее.
Дата добавления: 2014-12-24 ; Просмотров: 14747 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Как создать секретный код или шифр
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 79 человек(а).
Количество просмотров этой статьи: 76 396.
Обродай ожаловатьпай анай иптографиюкрай сай икихаувай! Независимо от того, пишите ли вы записки своим друзьям в классе или пытаетесь постигнуть криптографию (науку о кодах и шифрах) ради интереса, эта статья может помочь вам узнать некоторые основные принципы и создать свой собственный способ кодировки личных сообщений. Прочитайте шаг 1 ниже, чтобы понять с чего начинать!
Некоторые люди используют слова «код» и «шифр» для обозначения одинаковых понятий, но те, кто серьезно занимаются этим вопросом, знают, что это два абсолютно разных понятия. Секретный код – система, в которой каждое слово или фраза в вашем сообщении заменяются другим словом, фразой или серией символов. Шифр – система, в которой каждая буква вашего сообщения заменяется другой буквой или символом.
Цифровые, табличные шифры и шифры перестановки
Цифровые шифры
Таблица не обязательно должна выглядеть таким образом. Количество групп может быть другим. Также буквы из алфавита могут идти в таблице не по порядку.
Зашифруем таким способом слово «цифра»
Зашифрованный текст: 63 31 61 51 11
2) Цифровая таблица.
Зашифруем с помощью этой таблицы слово «наука».
Каждый символ будет шифроваться опять двумя цифрами, при чем первой может быть как номер столбца, так и номер строки. То есть буква К может быть зашифрована, как 32 или 23.
Зашифрованный текст: 62 11 33 32 11
3) Шифрование с заменой каждой буквы ее номером в алфавите. Очень простой вид шифра. Его, думаю, можно тоже отнести к цифровым. Но между тем, он часто применяется в различных вариациях и комбинациях с другими видами шифров. Про некоторые комбинации шифров расскажу чуть позже.
Квадрат Полибия
Похож на цифровую таблицу.
Здесь также составляется таблица, обычно число строк и столбцов берется одинаковое, но все зависит от алфавита. При нехватке клеток, можно списать в одну клетку сразу две буквы.
Пример квадрата Полибия для русского алфавита:
Далее шифрование с помощью таблицы может быть осуществлено тремя методами.
Вместо каждой буквы в шифруемом тексте используется соответствующая ей буква снизу (в таблице). Если буква находится в нижней строке, то она заменяется верхней буквой того же столбца. То есть, А => Е, Ю => Г, И => О и так далее.
Исходное слово: квадрат.
Зашифрованный текст: пзекчеш.
Исходное слово: квадрат.
Запишем координаты всех букв.
Считываем координаты по строкам: 53 15 11 22 11 14 14.
Заменяем буквы, пользуясь таблицей (квадратом). Получаем новую таблицу с координатами.
В итоге после шифрования у нас получается: пчаеарр
Снова записываются координаты букв, считываются по строчкам, но уже без пробелов, то есть записываются сплошным текстом. Получаем последовательность цифр, сдвигаем ее влево на один шаг. Например, было 134526, стало 345261 (то есть цифра из начала идет в конце последовательности). Затем разбиваем последовательность на пары: 34 52 61.
То есть, в случае шифрования слова «квадрат» (см. пример во 2 методе), у нас получится последовательность цифр: 53151122111414
Сдвигаем влево на один шаг: 31511221114145
Разбиваем на пары цифр: 31 51 12 21 11 41 45.
Заменяем цифры буквам согласно квадрату.
После шифрования у нас получается: вдебагю.
Также следует добавить, что возможны вариации квадрата Полибия. Буквы алфавита могут идти не по порядку, размер квадрата может быть другим, в третьем методе может быть выбрано другое смещение.
Основы криптографии: от математики до физики
Основы криптографии включают шифры, специальную терминологию и отдельные компоненты криптосистемы. Сегодня эта наука тесно связана с информационной безопасностью.
Примечание Вы читаете улучшенную версию некогда выпущенной нами статьи.
Задачи, которые решает криптография:
Популярные шифры
Чтобы понять основы шифрования, необходимо обратиться к популярным примерам.
Квадрат Полибия
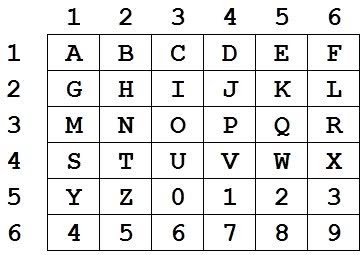
Квадрат Полибия — шифр простой замены. В данном примере будет использоваться двумерная матрица 6х6, содержащая заглавные буквы алфавита и цифры от 0 до 9:
С матрицей 6х6 (36 буквенно-цифровых знаков) мы можем начать замену. Например, буква «А» имеет адрес 1х1 или x=1, y=1. Эту запись можно упростить до 11. Другой пример: адрес буквы «N» будет 2х3 или x=2, y=3 или 23.
Шифр может сделать достаточно длинным и сложным, используя прописные буквы и специальные символы. Также повторение символов и написание алфавита вразброс может дать непредсказуемый результат, устойчивый для метода полного перебора.
Шифр Цезаря
Шифр Цезаря считается самым первым. Цезарь использовал его для кодирования сообщений своим генералам, чтобы враги из Римской Империи не смогли прочитать приказы при перехвате. Шифр Цезаря имеет элементарную форму шифрования, и сегодня его легко взломать: алфавит просто сдвигается вправо или влево. Разные значения сдвига приводят к разным результатам шифровки. Число сдвига — это число букв, на которое происходит смещение в одну из сторон, для создания шифротекста.
Пример использования шифра со сдвигом влево на 3:
Шифротекст выше может быть легко взломан методом полного перебора, который заключается в сдвиге в одну из сторон на одну позицию, пока не получится какое-то смысловое сообщение.
Прим. пер. Существует более простой способ взлома шифра Цезаря — частотный анализ. Он заключается в подсчёте частоты встреч каждого символа в любом обычном тексте и в шифротексте. Потом символы с похожими частотами заменяются. Например, если в шифротексте чаще всего встречается буква «T», то она заменяется на букву «Е» для английского алфавита. Этот способ действует только для текстов свыше 300 символов.
Квадрат Виженера
Это усовершенствованный шифр Цезаря с разными значениями сдвига. Например, к первой букве сообщения применяется преобразование ROT5, ко второй — ROT16, etc.
Также у нас есть статья, из которой вы узнаете о самых популярных кодах и шифрах.
Полиморфизм
Основы шифрования и криптографии включают в себя полиморфизм. Это более продвинутая практика в криптографии и часто используется в техниках компьютерного шифрования. Такая техника, которая самостоятельно модифицирует криптоалгоритм после каждого выполнения, и на каждой итерации получаются разные результаты. Если понадобится зашифровать одну и ту же информацию два раза, то алгоритм выдаст разные шифротексты.
Распространённые алгоритмы
Сегодня шифры используют алгоритмы либо с секретным, либо с публичным ключом. В шифрах с закрытым ключом используется единственный ключ, которым обмениваются стороны. Такой ключ или шифр также называют симметричным.
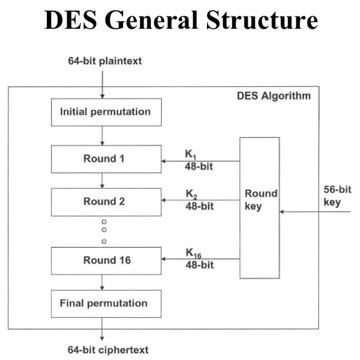
В 1949 году Клод Шеннон из Bell Laboratories опубликовал фундаментальную теорию, положившую начало симметричному шифрованию, а десятилетия эволюции принесли примеры высокого качества. Однако только в 1975 году мощный алгоритм с закрытым ключом DES стал доступен для общего пользования.
Шифрование с помощью открытого ключа или асимметричное шифрование также возникло в середине 1970-х. Асимметричные шифры используют пару ключей — открытый, им делятся с другими людьми, и соответствующий ему закрытый, пользователь должен хранить его в секрете от других.
Стойкость шифровального алгоритма зависит от трёх важных факторов:
Виды алгоритмов
DES выдержал испытание временем и вошёл в основы криптографии. После четверти века исследований учёным удалось найти несколько спекулятивных атак, которые в конечном итоге не были столь эффективными, как метод полного перебора. Единственная реальная слабость DES-шифра — маленькая длина ключа в 56 бит.
Triple DES (3DES) — модификация DES, позволяющая увеличить длину ключа до 112 или 168 бит.
AES (Advanced Encryption Standard или Rijndael) поддерживает три длины ключа: 128, 192 и 256 бит. Использует 128-битный размер блоков. Считается стойким и используется по всему миру.
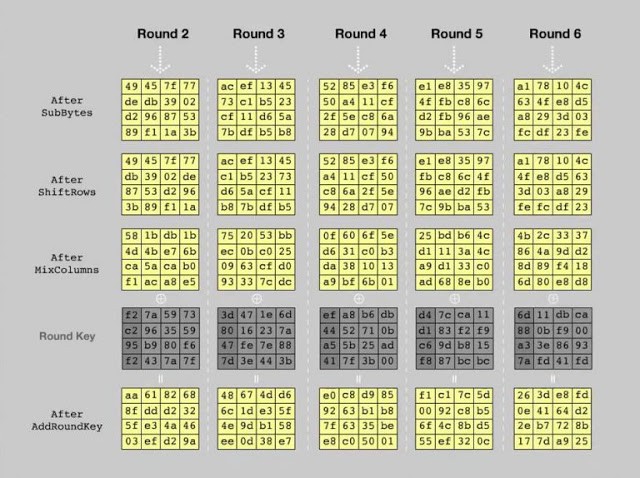
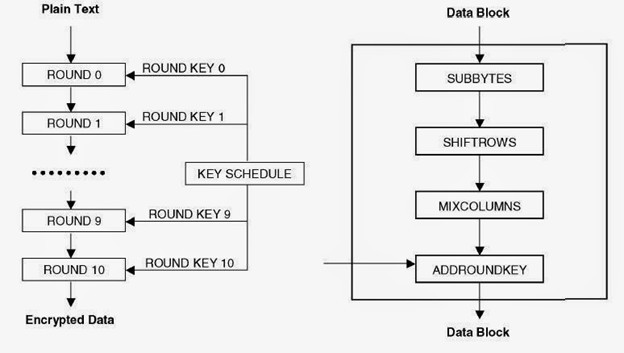
Алгоритм шифрования Rijndael (AES)
Так как DES был специально разработан для аппаратного обеспечения, то не было предусмотрено, чтобы он эффективно работал в ПО. NIST протестировал работу алгоритма AES в программной среде и разработал требования к хранению криптоматериала, чтобы гарантировать, что AES будет эффективно работать на C и Java, которые используются на рабочих станциях, а также в более ограниченных средах встроенных процессоров ARM и смарт-карт.
Архитектура AES основана на принципе, известном как замена и перестановка, и быстро работает как в программном, так и на аппаратном уровнях. В отличие от своего предшественника — DES, AES не использует сеть Фейстеля.
Длина ключа, используемого для шифрования AES, указывает на количество повторений раундов преобразования, которые преобразуют входной сигнал, называемый исходным текстом, а конечный вывод — шифротекстом. Число циклов повторения выглядит следующим образом:
Каждый раунд состоит из нескольких этапов обработки. Набор обратных повторений применяется для преобразования шифротекста в исходный текст с использованием того же самого ключа шифрования.
Квантовая криптография
Это уже не совсем основы криптографии, а более продвинутый уровень.
На приведённой диаграмме квантовое распределение ключей (протокол BB84), являющееся безопасным способом связи, который реализует криптографический протокол с участием компонентов квантовой механики. Он позволяет двум сторонам создавать общий закрытый ключ, известный только им.
Новое поколение криптографии будет основываться не на математике, а на физике. Учёные в области физики атомов и частиц уже вошли в мир основ криптографии и хотят использовать законы квантовой механики для отправки сообщений, которые невозможно взломать. Они основоположники новой науки — квантовой криптографии.
Классический криптоанализ
На протяжении многих веков люди придумывали хитроумные способы сокрытия информации — шифры, в то время как другие люди придумывали еще более хитроумные способы вскрытия информации — методы взлома.
В этом топике я хочу кратко пройтись по наиболее известным классическим методам шифрования и описать технику взлома каждого из них.
Шифр Цезаря
Самый легкий и один из самых известных классических шифров — шифр Цезаря отлично подойдет на роль аперитива.
Шифр Цезаря относится к группе так называемых одноалфавитных шифров подстановки. При использовании шифров этой группы «каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита» wiki.
Способы выбора ключей могут быть различны. В шифре Цезаря ключом служит произвольное число k, выбранное в интервале от 1 до 25. Каждая буква открытого текста заменяется буквой, стоящей на k знаков дальше нее в алфавите. К примеру, пусть ключом будет число 3. Тогда буква A английского алфавита будет заменена буквой D, буква B — буквой E и так далее.
Для наглядности зашифруем слово HABRAHABR шифром Цезаря с ключом k=7. Построим таблицу подстановок:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g |
И заменив каждую букву в тексте получим: C(‘HABRAHABR’, 7) = ‘OHIYHOHIY’.
При расшифровке каждая буква заменяется буквой, стоящей в алфавите на k знаков раньше: D(‘OHIYHOHIY’, 7) = ‘HABRAHABR’.
Криптоанализ шифра Цезаря
Малое пространство ключей (всего 25 вариантов) делает брут-форс самым эффективным и простым вариантом атаки.
Для вскрытия необходимо каждую букву шифртекста заменить буквой, стоящей на один знак левее в алфавите. Если в результате этого не удалось получить читаемое сообщение, то необходимо повторить действие, но уже сместив буквы на два знака левее. И так далее, пока в результате не получится читаемый текст.
Аффиный шифр
Рассмотрим немного более интересный одноалфавитный шифр подстановки под названием аффиный шифр. Он тоже реализует простую подстановку, но обеспечивает немного большее пространство ключей по сравнению с шифром Цезаря. В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0… m-1. Затем при помощи специальной формулы, вычисляется новое число, которое заменит старое в шифртексте.
Процесс шифрования можно описать следующей формулой:
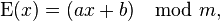
где x — номер шифруемой буквы в алфавите; m — размер алфавита; a, b — ключ шифрования.
Для расшифровки вычисляется другая функция:
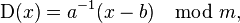
С учетом этого ограничения вычислим пространство ключей аффиного шифра на примере английского алфавита. Так как английский алфавит содержит 26 букв, то в качестве a может быть выбрано только взаимно простое с 26 число. Таких чисел всего двенадцать: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 и 25. Число b в свою очередь может принимать любое значение в интервале от 0 до 25, что в итоге дает нам 12*26 = 312 вариантов возможных ключей.
Криптоанализ аффиного шифра
Очевидно, что и в случае аффиного шифра простейшим способом взлома оказывается перебор всех возможных ключей. Но в результате перебора получится 312 различных текстов. Проанализировать такое количество сообщений можно и в ручную, но лучше автоматизировать этот процесс, используя такую характеристику как частота появления букв.
Давно известно, что буквы в естественных языках распределены не равномерно. К примеру, частоты появления букв английского языка в текстах имеют следующие значения:
Т.е. в английском тексте наиболее встречающимися буквами будут E, T, A. В то время как самыми редкими буквами являются J, Q, Z. Следовательно, посчитав частоту появления каждой буквы в тексте мы можем определить насколько частотная характеристика текста соответствует английскому языку.
Для этого необходимо вычислить значение:
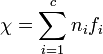
где ni — частота i-й буквы алфавита в естественном языке. И fi — частота i-й буквы в шифртексте.
Чем больше значение χ, тем больше вероятность того, что текст написан на естественном языке.
Таким образом, для взлома аффиного шифра достаточно перебрать 312 возможных ключей и вычислить значение χ для полученного в результате расшифровки текста. Текст, для которого значение χ окажется максимальным, с большой долей вероятности и является зашифрованным сообщением.
Разумеется следует учитывать, что метод не всегда работает с короткими сообщениями, в которых частотные характеристики могут сильно отличатся от характеристик естественного языка.
Шифр простой замены
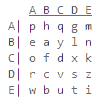
Очередной шифр, относящийся к группе одноалфавитных шифров подстановки. Ключом шифра служит перемешанный произвольным образом алфавит. Например, ключом может быть следующая последовательность букв: XFQABOLYWJGPMRVIHUSDZKNTEC.
При шифровании каждая буква в тексте заменяется по следующему правилу. Первая буква алфавита замещается первой буквой ключа, вторая буква алфавита — второй буквой ключа и так далее. В нашем примере буква A будет заменена на X, буква B на F.
При расшифровке буква сперва ищется в ключе и затем заменяется буквой стоящей в алфавите на той же позиции.
Криптоанализ шифра простой замены
Шифр Полибия
Еще один шифр подстановки. Ключом шифра является квадрат размером 5*5 (для английского языка), содержащий все буквы алфавита, кроме J.
При шифровании каждая буква исходного текста замещается парой символов, представляющих номер строки и номер столбца, в которых расположена замещаемая буква. Буква a будет замещена в шифртексте парой BB, буква b — парой EB и так далее. Так как ключ не содержит букву J, перед шифрованием в исходном тексте J следует заменить на I.
Например, зашифруем слово HABRAHABR. C(‘HABRAHABR’) = ‘AB BB EB DA BB AB BB EB DA’.
Криптоанализ шифра Полибия
Шифр имеет большое пространство ключей (25! = 2 83 для английского языка). Однако единственное отличие квадрата Полибия от предыдущего шифра заключается в том, что буква исходного текста замещается двумя символами.
Поэтому для атаки можно использовать методику, применяемую при взломе шифра простой замены — поиск восхождением к вершине.
В качестве основного ключа выбирается случайный квадрат размером 5*5. В ходе каждой итерации ключ подвергается незначительным изменениям и проверяется насколько распределение триграмм в тексте, полученном в результате расшифровки, соответствует распределению в естественном языке.
Перестановочный шифр
Помимо шифров подстановки, широкое распространение также получили перестановочные шифры. В качестве примера опишем Шифр вертикальной перестановки.
В процессе шифрования сообщение записывается в виде таблицы. Количество колонок таблицы определяется размером ключа. Например, зашифруем сообщение WE ARE DISCOVERED. FLEE AT ONCE с помощью ключа 632415.
Так как ключ содержит 6 цифр дополним сообщение до длины кратной 6 произвольно выбранными буквами QKJEU и запишем сообщение в таблицу, содержащую 6 колонок, слева направо:
Для получения шифртекста выпишем каждую колонку из таблицы в порядке, определяемом ключом: EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE.
При расшифровке текст записывается в таблицу по колонкам сверху вниз в порядке, определяемом ключом.
Криптоанализ перестановочного шифра
Лучшим способом атаки шифра вертикальной перестановки будет полный перебор всех возможных ключей малой длины (до 9 включительно — около 400 000 вариантов). В случае, если перебор не дал желаемых результатов, можно воспользоваться поиском восхождением к вершине.
Для каждого возможного значения длины осуществляется поиск наиболее правдоподобного ключа. Для оценки правдоподобности лучше использовать частоту появления триграмм. В результате возвращается ключ, обеспечивающий наиболее близкий к естественному языку текст расшифрованного сообщения.
Шифр Плейфера
Шифр Плейфера — подстановочный шифр, реализующий замену биграмм. Для шифрования необходим ключ, представляющий собой таблицу букв размером 5*5 (без буквы J).
Процесс шифрования сводится к поиску биграммы в таблице и замене ее на пару букв, образующих с исходной биграммой прямоугольник.
Рассмотрим, в качестве примера следующую таблицу, образующую ключ шифра Плейфера:
Зашифруем пару ‘WN’. Буква W расположена в первой строке и первой колонке. А буква N находится во второй строке и третьей колонке. Эти буквы образуют прямоугольник с углами W-E-S-N. Следовательно, при шифровании биграмма WN преобразовывается в биграмму ES.
В случае, если буквы расположены в одной строке или колонке, результатом шифрования является биграмма расположенная на одну позицию правее/ниже. Например, биграмма NG преобразовывается в биграмму GP.
Криптоанализ шифра Плейфера
Так как ключ шифра Плейфера представляет собой таблицу, содержащую 25 букв английского алфавита, можно ошибочно предположить, что метод поиска восхождением к вершине — лучший способ взлома данного шифра. К сожалению, этот метод не будет работать. Достигнув определенного уровня соответствия текста, алгоритм застрянет в точке локального максимума и не сможет продолжить поиск.
Чтобы успешно взломать шифр Плейфера лучше воспользоваться алгоритмом имитации отжига.
Отличие алгоритма имитации отжига от поиска восхождением к вершине заключается в том, что последний на пути к правильному решению никогда не принимает в качестве возможного решения более слабые варианты. В то время как алгоритм имитации отжига периодически откатывается назад к менее вероятным решениям, что увеличивает шансы на конечный успех.
Суть алгоритма сводится к следующим действиям:
Для расчета коэффициентов, определяющих принадлежность текста к естественному языку лучше всего использовать частоты появления триграмм.
Шифр Виженера
Шифр Виженера относится к группе полиалфавитных шифров подстановки. Это значит, что в зависимости от ключа одна и та же буква открытого текста может быть зашифрована в разные символы. Такая техника шифрования скрывает все частотные характеристики текста и затрудняет криптоанализ.
Шифр Виженера представляет собой последовательность нескольких шифров Цезаря с различными ключами.
Продемонстрируем, в качестве примера, шифрование слова HABRAHABR с помощью ключа 123. Запишем ключ под исходным текстом, повторив его требуемое количество раз:
Цифры ключа определяют на сколько позиций необходимо сдвинуть букву в алфавите для получения шифртекста. Букву H необходимо сместить на одну позицию — в результате получается буква I, букву A на 2 позиции — буква C, и так далее. Осуществив все подстановки, получим в результате шифртекст: ICESCKBDU.
Криптоанализ шифра Виженера
Первая задача, стоящая при криптоанализе шифра Виженера заключается в нахождении длины, использованного при шифровании, ключа.
Для этого можно воспользоваться индексом совпадений.
Индекс совпадений — число, характеризующее вероятность того, что две произвольно выбранные из текста буквы окажутся одинаковы.
Для любого текста индекс совпадений вычисляется по формуле:
,
где fi — количество появлений i-й буквы алфавита в тексте, а n — количество букв в тексте.
Для английского языка индекс совпадений имеет значение 0.0667, в то время как для случайного набора букв этот показатель равен 0.038.
Более того, для текста зашифрованного с помощью одноалфавитной подстановки, индекс совпадений также равен 0.0667. Это объясняется тем, что количество различных букв в тексте остается неизменным.
Это свойство используется для нахождения длины ключа шифра Виженера. Из шифртекста по очереди выбираются каждая вторая буквы и для полученного текста считается индекс совпадений. Если результат примерно соответствует индексу совпадений естественного языка, значит длина ключа равна двум. В противном случае из шифртекста выбирается каждая третья буква и опять считается индекс совпадений. Процесс повторяется пока высокое значение индекса совпадений не укажет на длину ключа.
Успешность метода объясняется тем, что если длина ключа угадана верно, то выбранные буквы образуют шифртекст, зашифрованный простым шифром Цезаря. И индекс совпадений должен быть приблизительно соответствовать индексу совпадений естественного языка.
После того как длина ключа будет найдена взлом сводится к вскрытию нескольких шифров Цезаря. Для этого можно использовать способ, описанный в первом разделе данного топика.
Исходники всех вышеописанных шифров и атак на них можно посмотреть на GitHub.
Игра в шифровальщика: вашим детям это понравится
Приблизительное время чтения: 12 мин.
Для многих игр с детьми — и настольных, и онлайновых, и ролевых — можно использовать шифры. Это не только вызывает у детей интерес, но и развивает внимание, аккуратность, абстрактное мышление, навыки устного счета и осмысленного чтения.
С детьми из скаутского отряда «Сполох» я уже почти пять лет веду занятия по методам шифрования — полученные навыки потом применяются для отрядных игр, но и сами по себе шифры интересны детям младшего и среднего школьного возраста, они с огромным увлечением разгадывают «таинственные» послания и пишут их друг другу. А к тому же, когда коллективу детей приходится прочитать зашифрованный текст, тренируются и навыки взаимодействия в команде, распределения работы, достижения общей цели.
Конечно, этим же можно заниматься с детьми и в семье. Но сразу хочу предупредить родителей: если дети втянутся, то поначалу вам придется то и дело разгадывать их зашифрованные записки и отвечать им тем же. Иначе говоря — поддерживать формат развивающей интеллектуальной игры.
История, которую предварительно нужно рассказать детям
Шифрование — то есть сокрытие информации — появилось еще в древние времена. А уж когда возникли государства, армии, войны, разведка — то возникла необходимость тайно передавать какие-то сведения, чтобы, если вдруг они попадутся в руки врагу, тот ничего бы не понял. Нужны были тайные знаки, чтобы узнавать своих. Например, разрезали на части монету. Люди могли никогда друг друга не видеть, но если посланец предъявлял свою половинку, и при наложении обе части совпадали, значит, это свой.
А еще такой секретный знак был у первых христиан — в те века, когда за исповедание христианской веры тебя могли казнить. Как христиане могли узнавать своих — так, чтобы никто их не заподозрил и не выдал властям? У христиан был священный знак, символическое изображение рыбы (потому что если прочитать первые буквы фразы по-гречески «Иисус Христос Божий Сын Спаситель», то получалось греческое слово «ихтис», что значило рыба). Поэтому один христианин мог начертить тростью на земле дугу — сама по себе дуга еще ничего не обозначала. Но второй христианин в ответ на это чертил другую дугу, которые вместе складывались в изображение рыбы. Вот так:
И оба понимали, что они — единоверцы. А со стороны никто бы ничего не понял.
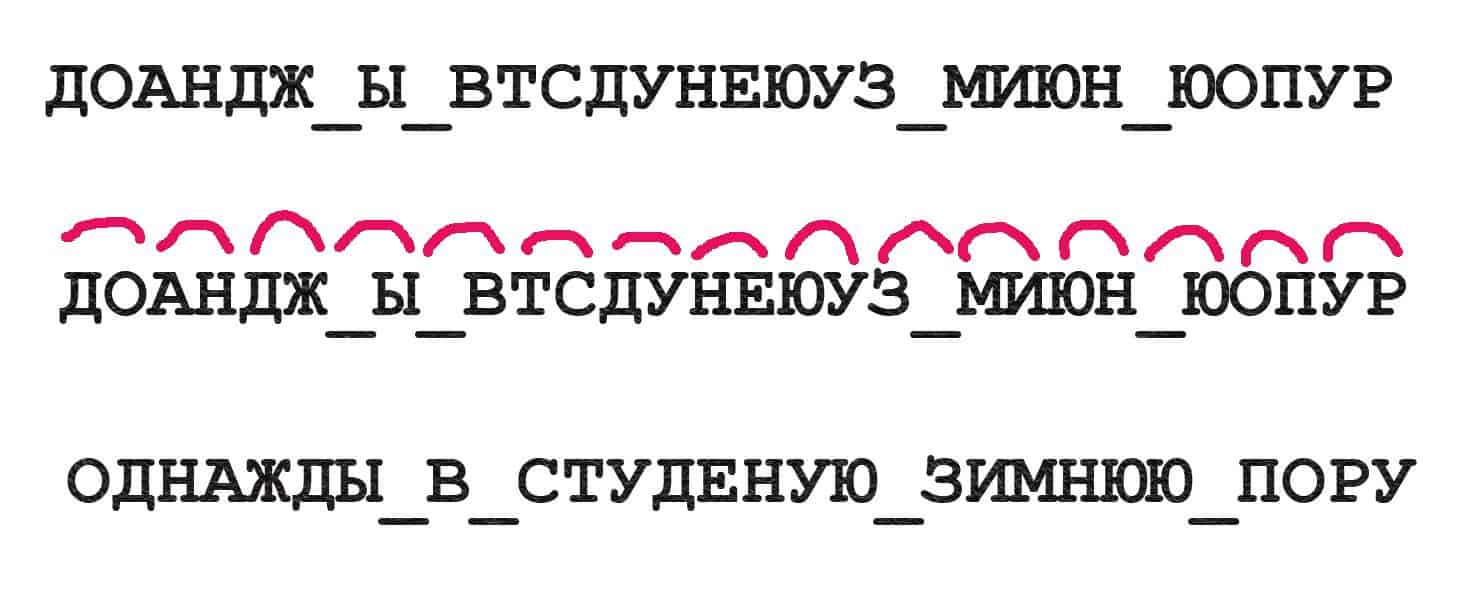
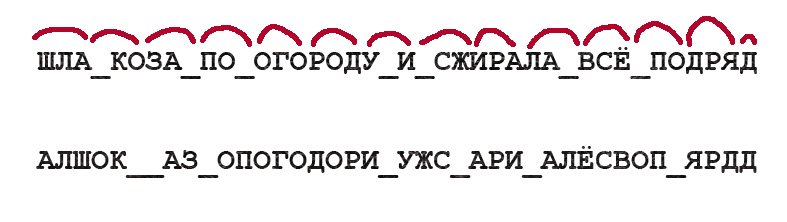
В древности люди еще и придумывали «тайные языки», на которых можно было устно разговаривать, и никто из посторонних не мог понять эту «тарабарщину». В старину на Руси были такие люди, которые назывались офени. Это бродячие торговцы разным мелким товаром — гребнями, бусами, нитками, пуговицами, ленточками, иголками, ножницами и так далее. Но они не только занимались торговлей, но подчас выведывали разные тайны, то есть торговля у них служила лишь прикрытием для разведки. И вот между собой они говорили на специальном языке — брали слово и переставляли местами слоги. Если слово двусложное, то сперва говорили второй слог, потом первый. Не «палка», а «капал», не «рыба», а «бары». Если слово трехсложное, то сперва говорили третий слог, потом второй, потом первый. Вместо «рыбалка» было «кабалры». Ну и так далее:
Были и другие старинные шифры. Например, слова писались не слева направо, а справа налево. Не «капуста», а «атсупак», не «бабушка», а «акшубаб». Вот, например:
Еще в старину часто использовали шифр, когда буквы в слове писались в зеркальном отражении. Прочитать такой текст можно было, только поднеся его к зеркалу:
Но это всё довольно простые шифры, которые очень легко разгадать. А были и посложнее, о них-то пойдет речь.
Криптография и стеганография
Затем детям надо рассказать, что есть два разных способа тайно передавать сообщение. Первый — это криптография (от греческого «криптос» — тайна и «графо» — пишу), в переводе на русский «тайнопись». Идея в том, что мы каким-то хитрым образом искажаем текст, который хотим скрыть, и кто этого способа не знает, не сможет его восстановить. Второй способ называется стеганография (от греческого «стеганос» — скрытый и «графо» — пишу). Здесь мы поступаем хитрее — никак не изменяем сам текст, который хотим передать, но прячем его среди ненужной информации.
Например, используем так называемые стеганографические решетки. Это прямоугольные рамки, в которых хаотично прорезаны квадратики. Вот так:
Накладываем эту рамку на лист бумаги (так, чтобы цветной квадратик был в верхнем левом углу) и вписываем в прорези то сообщение, которое хотим спрятать. Без знаков препинания и без пробелов. Например:
Потом снимаем решетку и вписываем между букв нашего сообщения произвольные буквы и цифры. Например:
Совершенно бессмысленный текст, в котором нужное сообщение спрятано среди ненужного хлама. Но у кого есть точно такая же решетка, наложит ее на эту бумажку (выделенный квадратик — в левом верхнем углу) и прочитает те буквы, которые будут видны в прорезях.
Полезное упражнение: сделать вместе с детьми такие решетки (две одинаковых) и обмениваться тайными посланиями. Чтобы решетки получились полностью одинаковыми, нужно сперва сделать одну, потом наложить на кусок картона такого же размера, обвести карандашом все прорези и вырезать их ножницами. Если дети совсем маленькие, процесс, конечно, следует контролировать.
Какие бывают шифры
Конечно, здесь речь идет не о современных способах шифровки, которые основаны на очень серьезных математических методах и реализуются с помощью специальных компьютерных программ. С детьми мы занимаемся старинными шифрами, где для расшифровки достаточно лишь бумаги, ручки и мозгов.
Такие шифры делятся на две группы — перестановочные и подстановочные.
Идея перестановочных шифров — мы по какому-то правилу переставляем местами буквы в шифруемой строке. Если заранее знать, какое это правило (или догадаться), то можно переставить буквы так, чтобы получить исходную строку.
Идея подстановочных шифров — мы по какому-то правилу подставляем вместе каждой буквы в строке другую какую-то букву. Это может быть буква того же алфавита, а может быть буква специально придуманного (как, например, в рассказе Конан Дойля «Пляшущие человечки» из цикла о Шерлоке Холмсе).
Полезное упражнение: придумать вместе с детьми такие алфавиты, где каждой русской букве соответствует какой-то значок. Например, так:
Или, например, так:
Важное замечание
Для удобства при шифрованиии мы не различаем прописных и строчных букв (все слова пишем прописными), не используем знаков препинания, все числа пишем словами и (что особенно важно в перестановочных шифрах) обозначаем пропуск между словами знаком нижнего подчёркивания: «_». Детям надо сразу сказать, что пробел — такой же важный знак, как и буквы, если про него забыть, то обязательно ошибешься с зашифровкой и расшифровкой. То есть текст, подготовленный для зашифровки, должен выглядеть примерно так (стихотворение Семёна Липкина):
Простейшие перестановочные шифры
Самый простой перестановочный шифр называется «перестановка по два». Идея заключается в том, что мы разделяем строку на группы из двух знаков, и в каждой из групп меняем их местами. Если количество знаков нечётное, то последний знак не трогаем, оставляем как есть.
Пробел, обозначаемый знаком нижнего подчёркивания, тоже считается знаком — таким же, как и буквы.
Расшифровка делается точно так же, как и зашифровка: выделяем группы по два знака и внутри групп меняем их местами:
Чуть более хитрый перестановочный шифр называется «перестановка по три». Тут мы разделяем строку на группы по три знака, и для зашифровки записываем эти знаки справа налево. Например:
Обратите внимание: у нас встретилось в шифровке два пробела подряд. Надо замечать такие вещи и понимать, что это ДВА пробела.
Расшифровка происходит точно так же, как и зашифровка: с начала строки, т.е. слева направо, выделяем группы по три знака, и записываем в каждой группе их справа налево:
Обратите внимание: на конце строки может остаться один знак, не попавший в группу по три, и тогда мы его не трогаем, или два знака, и тогда мы просто меняем их местами.
Разумеется, ничто не мешает делать перестановки по четыре знака, по пять, и так далее. Очень хорошо, если дети самостоятельно додумаются до этой идеи. Но практика показывает, что такое бывает нечасто, перестановок по два и по три обычно вполне достаточно и для занятий, и для игр.
Простейшие подстановочные шифры
Можно, конечно, применять придуманные алфавиты, а можно по определенному правилу подставлять вместо шифруемой буквы другую букву русского алфавита.
Самое простое и самое известное из таких правил называется «плюс один». Идея заключается в том, что вместо шифруемой буквы мы подставляем следующую по алфавиту. Вместо «А» — «Б», вместо «Б» — «В», и так далее. А вместо «Я» — подставляем «А».
Вот так делается шифровка методом «плюс один»:
Обратите внимание — здесь пробел можно не обозначать нижним подчеркиванием, потому что при подстановочных шифрах пробел остается пробелом.
Расшифровка происходит наоборот: каждую букву в зашифрованной строчке мы заменяем на предыдущую в алфавите. А если это была буква «А», то заменяем ее на «Я». Вот так:
И, конечно, можно зашифровывать, беря вместо каждой буквы предыдущую, а расшифровывать — заменяя каждую букву шифровки следующей по алфавиту. Такой шифр назовем «минус один».
Заметим: для расшифровки текста, зашифрованного методом «плюс один», мы применяем метод «минус один», и наоборот.
Точно так же можно применять шифр «плюс два», когда вместо «А» пишем «В», вместо «Б» — «Г», и так далее, вместо «Э» — «Я», вместо «Ю» — «А», вместо «Я» — «Б». Но переходить к таким шифрам надо только после того, как дети уже хорошо освоили «плюс один» и «минус один».
И, конечно, для работы с подстановочными шифрами нужно хорошо помнить алфавит. Если наизусть его не помнят, не грех пользоваться бумажкой:
Буквы алфавита тут пронумерованы, и это не случайно. В некоторых шифрах, более сложных, нужно использовать порядковый номер буквы.
Есть и более сложные шифры — и подстановочные, и перестановочные — которые тоже можно освоить с детьми и применять для игр. Но об этом в другой раз.
Как применять шифры для игр
Если просто взять ребенка, усадить перед собой и начать изучать с ним шифры — скорее всего, ему это быстро наскучит, потому что он не понимает, зачем все это надо. То есть не будет мотивации. Поэтому начинать надо именно с игр. Например, подкинуть ребенку «таинственное письмо» — коротенькое и простенькое, но с интересным, веселым содержанием. Какой-нибудь смешной стишок, или информация, где спрятана конфета. в общем, родители сами сообразят. Когда ребенок самостоятельно (или с подсказками) прочитает послание — вот тогда уже следует говорить с ним про новую игру — шифры — и изучать их.
Причем изучать не за один раз. Сперва можно поговорить про старинные шифры, в другой раз — про стегагографические решетки (и обязательно своими руками сделать пару таких решеток). Потом — посочинять свои алфавиты и обязательно писать друг другу письма с их помощью. И только потом можно осваивать перестановочные шифры, затем — подстановочные.
С какого возраста можно обучать детей шифрам? Это зависит от их развития. Мне и с шестилетками приходилось этим заниматься. Но общий принцип — начинать надо тогда, когда ребенок уже вполне бегло читает и пишет, то есть обычно это со второго класса.
И, конечно, все эти навыки тут же надо применять к играм. Например, освоили перестановочный шифр — тут же рисуем (вместе с ребенком!) карту какой-нибудь волшебной страны и подписываем перестановочным шифром название городов, стран, рек, морей.
Или придумываем каких-то героев (можно взять просто традиционных героев русских сказок) и придумываем их зашифрованную переписку. Например, Лиса пишет зайцу:
РПХИДО_ИОКМ_ЕНЯ_Д_МАТ_БЕ_ЕТС_ОКВСУЫН_ХОМКРВОКО
(Приходи ко мне, я дам тебе сто вкусных морковок)
Ребенок расшифровывает это письмо Лисы и пишет ответ Зайца:
ЕНВ_РЕ_Ю_ЯЕТЕБЛ_СИ_АЫТМ_НЕ_ЯЪССЕЬТХ_ЧОШЕЬ
(Не верю я тебе, ты меня съесть хочешь)
И дальше продолжается эта переписка.
Можно еще сочетать творческие игры, где ребенок сочиняет какие-то истории, с заданиями на шифровку. Допустим, он сочиняет сказку про детектива Кролика, который расследует похищение Медведя и обнаруживает в его опустевшей берлоге зашифрованную записку. Какую? А это ребенок придумает сам. И зашифрует.
Очень хорошо придумывать вместе с ребенком какие-нибудь настольные игры-бродилки, где что-то надо расшифровывать. Например, это может быть игра, которую мы делаем в подарок каким-то другим детям. Младшим братьям или сестрам, друзьям, одноклассникам.
В общем, навыки шифрования — это полезный инструмент, который можно применять для самых разных игр и развивающих активностей. Это как соль — она ценна не сама по себе, а как приправа для пищи.
ПРИЛОЖЕНИЕ
Упражнения для расшифровки
ЕНУС_ТЕМЯНХ_ДОЛУИ
РКЧИТАР_БЕТЯ_АЛСЗАЬ
ОБСЮ_ЬЕНУ_АПУДЛ_И
_СОХУДЕЛЙ
РПМЯ_О_ВРГЗЯЬ
_ИРСЗА_УОПАЗУБУДТ
АК_КАВНЖ_О_ЯОХИДЛ
ОНД_ЛООГП_МОИНЬТБ_ДУТУ
УКАДЯ_У_ОГИДЛ
Cтихотворение Валентина Берестова:
Несут меня ходули.
Кричат ребята: «Слазь!»
Боюсь, не упаду ли
И сразу позабудут,
Как важно я ходил,
Но долго помнить будут,
ЕНМРН_ИВАЯСТЕН_УД_ТАМО_ЬЛП_ОХОМ
КАКУБ_ОТДОВ_ЕСВЕН_ЫБ_ _ОЛОЛПГОХО
КАКУБ_ОТДАН_ИЛ_ЕТСОС_ЕСВП_МТСУМО
Н_ЯИЧАЮАНРП_ИВАНЬЛ_ЕООЛСОВ
О_ЯАТСЯЛВС_ЮРАТ_ЕЫИШОИКБ
П_ВАЗОЕЧВШАРЙЕНУМ_РОСЙОНОК_ИЗРЕКН
Ч_СНРЕИВОМОКАЗ_НОКНЕЧГОНД_ОЯН
_ОНРДВ_ГУИОМАЗ_ТЫБ_ЕЫИШОИКБ
ТТОИГЯЯАВ_ЬСДУБ_ОТ_АНЗЕРКНИЕ
ЫРСЮАВЯСТ_И_УТСЮАКМ_ТЯНЕ
Cтихотворение Дениса Маслакова:
Мне нравится не думать о плохом,
Как будто вовсе не было плохого,
Как будто на листе совсем пустом
Я начинаю правильное слово.
Я оставляю старые ошибки
В позавчерашней мусорной корзинке
С черновиком законченного дня.
Но вдруг мои забытые ошибки
Оттягиваясь, будто на резинке,
Срываются и стукают меня.
А ЛБНФЩЁЛ ЕЙГОЬК
ОБЩЖМ ОБ СЁЛЁ
А ТРЙОЛФ ЁНФ
ТПДСЁГБЯ Г СФЛЁ
ГЁЕЭ ЛБНФЩЁЛ ЮУПУ
ОБГЁСОП ГПГЁЛ
Г СФЛБЦ ОЁ ЕЁСЗБМ
ОЙ ПЕЙО ШЁМПГЁЛ
Стихотворение Анастасии Орловой:
Я камушек дивный
Согреваю в руке.
Ведь камушек этот,
В руках не держал
Ни один человек!
МЯ ЦДСЪПЕФ ЙНКЕРЯФ
ЙЯСЯЭС ЛЯКЪЧЯ
ГПТВНИ МЯ СПЕФ ОПНДФЯК
ЙТГЯСН МД РОДЧЯ
МЯ ГБТФ МДРЕСРЮ СПДСЗИ
ЛЯКЭРДМЫЙЗИ ЙЯЙ ВМНЛ
Я Ю ЙЯЦТРЫ МЯГ МЗЛЗ
МЯ ЙНКДРД НГМНЛ
Стихотворение Галины Дядиной:
На четырёх колёсах
Другой на трёх проехал
Куда-то, не спеша.
На двух несётся третий –
Малюсенький, как гном.
А я качусь над ними –
На колесе одном.
ПВО ИВНМР ЁЖЁХЪМХ МРТПЖБ
Д УТВДПЖПЮЖ У ПВОК РП РФУФВН
СРУМРНЮМХ Д ЁЖФУФДЖ ГВТОВНЖБ
К ОРЛЁРЁЭТВ ПЖ ЩКФВН
ПЖ ДРУЧКЫВНУБ ФЖНЖЦРПРО
К Д ФВТВМВПКЫЖ ПЖ ДПКМ
МВМ ДЭТРУ РП ФВМКО ХЩЗПЭО
ПЖ ЙПВБ УВОЭЧ ЕНВДПЭЧ МПКЕ