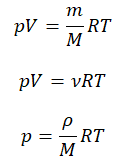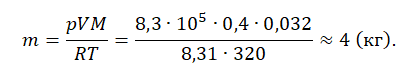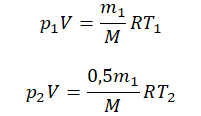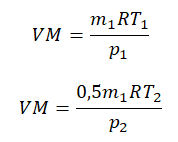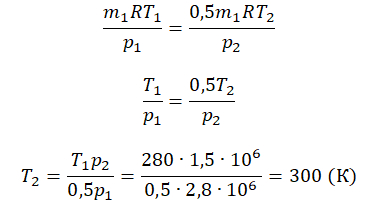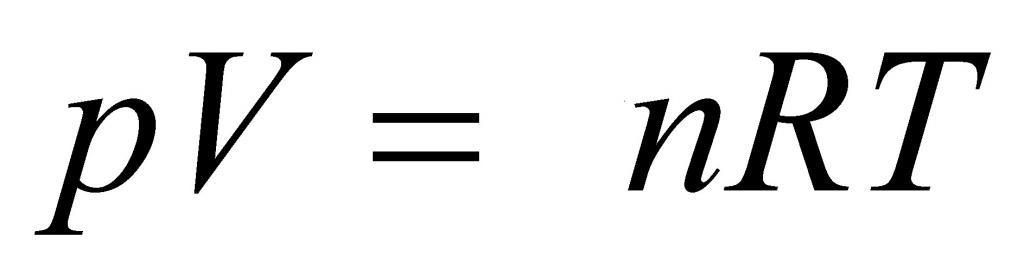какая форма уравнения состояния содержит больше информации уравнение клапейрона или менделеева

Какая форма уравнения состояния содержит больше информации уравнение клапейрона или менделеева

где N_А — число Авогадро, k — постоянная Больцмана.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

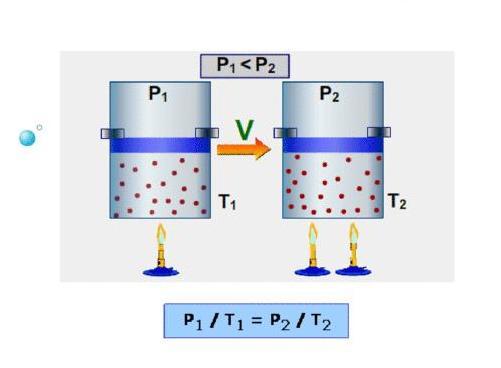
V= const => p/T = const — закон Шарля

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Источник

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза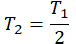
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул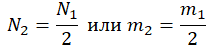
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы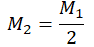
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

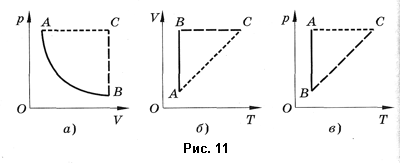
График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Источник

Какая форма уравнения состояния содержит больше информации уравнение клапейрона или менделеева

Физика → Методика → Экзамены → Ответы на билеты устных экзаменов → 8. Уравнение состояния идеального газа (уравнение Менделеева—Клапейрона). Изопроцессы8. Уравнение состояния идеального газа (уравнение Менделеева—Клапейрона). Изопроцессы

Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти неличины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.

Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона:

,

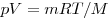
где — давление, — объем, — массa, — молярная масса, — универсальная газовая постоянная (). Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К.

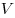
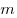
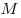
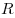
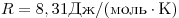
Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.

Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.

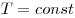
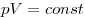
Изотермическим называют процесс, протекаю-щий при постоянной температуре: . Он описывается законом Бойля—Мариотта: .

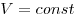
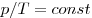
Изохорным называют процесс, протекающий при постоянном объеме: . Для него справедлив закон Шарля: .

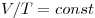
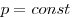
Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид при и называется законом Гей-Люссака. Все изопроцессы можно изобразить графически. На рисунке 11 представлены в различных координатах графики процессов: изотермического (изотерма АВ), изобарного (изобара АС) и изохорного (изохора ВС).

Реальные газы удовлетворяют уравнению состоя ния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежимо мал по сравнению с объемом сосуда, в котором находится газ) и при не слишком низких температуpax (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.

Источник

Закон Клапейрона-Менделеева для идеального газа: исторические предпосылки, формула, пример задачи

Рассмотрение свойств газов в физике в первом приближении основывается на концепции идеального газа. В данной статье подробно изучим эту концепцию и приведем уравнение, которое описывает численно термодинамические свойства упомянутой текучей субстанции. Это уравнение называется законом Клапейрона-Менделеева.

Концепция идеального газа

В школьном курсе физики газовое агрегатное состояние вещества характеризуется произвольным перемещением с различными скоростями всех составляющих его атомов и молекул. Эти частицы считаются в первом приближении абсолютно упругими материальными точками. Они имеют массу, но не размеры. Весь характер их взаимодействия друг с другом заключается в абсолютно упругих столкновениях, в результате которых сохраняется количество движения и энергия. Все перечисленные свойства частиц и их приближения образуют концепцию идеального газа.

Вам будет интересно: Каково значение слова «сострадание»?

Любой реальный газ, будь то гелий, кислород или воздух, можно с высокой точностью считать идеальным, если его давление составляет порядка одной атмосферы и ниже, а температура соответствует комнатной или выше. Если эти условия не выполняются, то газ считается реальным, и для его описания следует использовать уравнение Ван-дер-Ваальса, а не закон Клапейрона-Менделеева, о котором пойдет речь далее в статье.

Предпосылки возникновения уравнения состояния идеального газа

Под уравнением состояния газа идеального принято понимать математическую формулировку газового закона Менделеева-Клапейрона. Как и любое открытие в физике, это уравнение не появилось из неоткуда, а имело вполне определенные исторические предпосылки.

В 60-70-е годы XVII века англичанин Роберт Бойль и француз Эдм Мариотт независимо друг от друга в результате многих проведенных экспериментов с различными газами установили, что произведение объема на давление для закрытой системы с газом остается постоянным для любых процессов, в результате которых температура не изменяется. В настоящее время этот газовый закон носит фамилии названных ученых.

Наконец, в 1834 году Эмиль Клапейрон вывел, анализируя открытые предыдущими учеными газовые законы, уравнение Клапейрона. Менделеева фамилия появилась в названии этого уравнения благодаря его вкладу в преобразование исходного выражения к современному виду. В частности, Менделеев ввел понятие универсальной газовой постоянной.

Формула закона Клапейрона-Менделеева

Выше мы дали определение идеального газа, рассказали о законах, которые привели к формулировке универсального уравнения состояния. Теперь пришло время записать это уравнение:

Коэффициентом пропорциональности является уже упомянутая универсальная постоянная R. Она равна 8,314 Дж/(моль*К). Если 1 моль газа нагреть на 1 кельвин, то в процессе расширения он совершит работу 8,314 Джоуля. Любопытно заметить, что универсальной величина R называется потому, что она не определяется химической природой газа. Для всех чистых газов и их смесей она принимает единственное значение.

Откуда выводится изучаемое уравнение?

Выше мы уже сказали, что Клапейрон свое уравнение получил в результате банального обобщения экспериментальных результатов различных ученых. Тем не менее, закон Клапейрона-Менделеева может быть получен чисто теоретическими методами.

Одним из них является МКТ (молекулярно-кинетическая теория). МКТ рассматривает газовую систему с точки зрения концентрации частиц, распределения их скоростей, учета их масс и следование концепции идеального газа. Универсальное уравнение газа однозначно следует, если применить второй закон Ньютона к процессу упругого соударения частиц со стенками герметичного сосуда. В результате применения МКТ получается выражение:

Это равенство приводит к записанному в предыдущем пункте уравнению, если учесть следующие выражения:

Использование универсального уравнения для решения задачи

Известно, что некоторый газ под давление 2 атмосферы находится в баллоне при температуре 25 oC. Объем баллона составляет 50 литров. Какое количество вещества содержится в баллоне?

Поскольку нам известны 3 из 4-х параметров, то можно применить закон Клапейрона-Менделеева, чтобы найти величину n. Прежде чем это сделать, переведем все единицы в систему СИ:

P = 2 атм. = 101325*2 = 202650 Па;

T = 25 + 273,15 = 298,15 К;

Теперь воспользуемся формулой, получим:

n = P*V/(R*T) = 202650*0,05/(8,314*298,15) = 4,09 моль.

Хотя само значение 4,09 моль является небольшим, количество частиц газа будет гигантским. Чтобы его получить, следует n умножить на NA=6,02*1023.

Источник

Правила применения уравнения состояния идеальных газов

Идеальный газ — что это за состояние

Идеальный газ — это газ, в котором пренебрегают потенциальным взаимодействием молекул газа между собой. Считается, что молекулы газа не сталкиваются друг с другом, а только со стенками сосуда.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, широко применяемая для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Когда используют модель идеального газа, то предполагается:

Таким образом, между частицами газа нет дальнодействующего взаимодействия, например, электростатического и гравитационного. Дополнительное условия упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа.

Газ находится в термодинамическом равновесии со стенками сосуда и дополнительно отсутствуют макроскопические потоки вещества.

Тут следует уточнить, что градиенты термодинамических величин могут иметь место, как например, при включении внешнего поля, к примеру, гравитационного.

Таблица 1. Допущения, которые лежат в основе молекулярно-кинетической теории описания физической модели идеального газа.

Особенности, каким уравнением выражается

Соотношение, при котором определяется связь параметров состояния друг с другом, называется уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров:

Масса тела или системы, как правило, известна.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака.

Уравнение Менделеева-Клапейрона

Термические свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

Правила применения для решения задач

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех параметров (давление, температура или объем) остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из параметров состояния: давление, объем, температура или энтропия — остаются неизменными.

В зависимости от того, какой параметр остается неизменным, различают разные процессы:

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания постоянной температуры газа необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется законом Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

В изотермических условиях проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа можно применить в задачах.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс и мы можем воспользоваться для решения законом Бойля-Мариотта.

Откуда можем найти начальный объем:

Ответ: первоначальный объем газа был равен 8 л.

Объем пузырька воздуха при всплытии со дна озера на поверхность увеличился в 2 раза. Какова глубина озера?

Так как в условиях не говорится про изменение температуры в ходе данного процесса, то мы принимаем, что это изотермический процесс и можно использовать закон Бойля-Мариотта.

Где p 1 = ρ g h + p 0 — давление воздуха внутри пузырька в начальном состоянии (до всплытия), а V_1 — объем газа в начальном состоянии.

p_2= p_0 — давление воздуха внутри пузырька газа в конечном состоянии (на поверхности водоема).

V_2 = 2 V_1 — объем пузырька воздуха в конечном состоянии.

ρ — плотность воды, h — глубина водоема, p_0 — нормальное атмосферное давление, g = 9,8 м/с^2 — ускорение свободного падения.

( ρ g h + p 0 ) V 1 = 2 p 0 V 1

Откуда находим высоту, которая и является глубиной озера:

Берем давление при нормальных условиях в единицах системы СИ, то есть

Ответ: глубина озера 10,2 м.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянном объеме равно отношению его абсолютных температур:

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме графически изображается прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Рассмотрим правила применения изохорного режима для решения задач.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

Источник

• ← Как сделать лизинг своими руками
• Как сделать макияж глаз стойким →