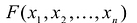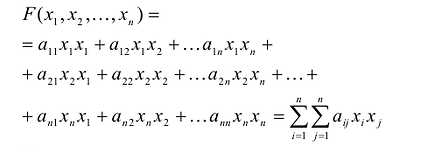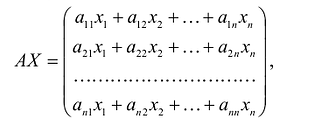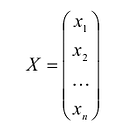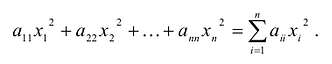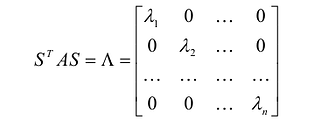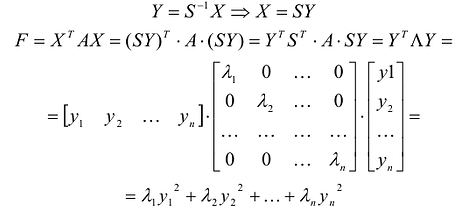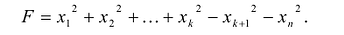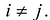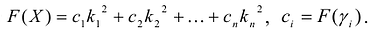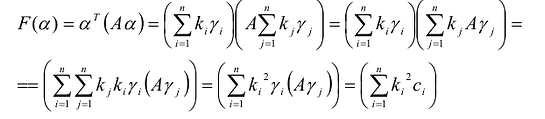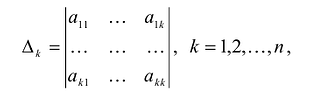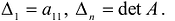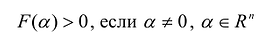какая квадратичная форма называется положительно определенной

Положительно определенные квадратичные формы

Определение. Квадратичная форма называется положительно определенной, если все ее значения при вещественных значениях переменных, не равных одновременно нулю, положительны. Очевидно, что квадратичная форма положительно определена.

Определение. Квадратичная форма называется отрицательно определенной, если все ее значения отрицательны, за исключением ненулевого значения при ненулевых значениях переменных.

Определение. Квадратичная форма называется положительно (отрицательно) полуопределенной, если она не принимает отрицательных (положительных) значений.

Квадратичные формы, принимающие как положительные, так и отрицательные значения, называются неопределенными.

При n=1 квадратичная форма либо положительно определена (при ), либо отрицательно определена (при ). Неопределенные формы появляются при .

Теорема (критерий Сильвестра положительной определенности квадратичной формы). Для того, чтобы квадратичная форма

была положительно определена, необходимо и достаточно выполнение условий:

.

Доказательство. Используем индукцию по числу переменных, входящих в . Для квадратичной формы, зависящей от одной переменной , и утверждение теоремы очевидно. Положим, что утверждение теоремы справедливо для квадратичной формы , зависящей от n-1 переменных .

1. Доказательство необходимости. Пусть

положительно определена. Тогда квадратичная форма

будет положительно определенной, так как если , то при .

По предположению индукции все главные миноры формы положительны, т.е.

.

Остается доказать, что .

Положительно определенная квадратичная форма невырожденным линейным преобразованием Х=ВY приводится к каноническому виду

.

Квадратичной форме соответствует диагональная матрица

с определителем .

Линейное преобразование, заданное невырожденной матрицей В, преобразует матрицу С квадратичной формы в матрицу . Но так как то .

2. Доказательство достаточности. Предположим, что все главные миноры квадратичной формы положительны: .

Докажем, что квадратичная форма положительно определена. Из предположения индукции вытекает положительная определенность квадратичной формы . Поэтому невырожденным линейным преобразованием приводится к нормальному виду . Сделав соответствующую замену переменных и положив , получим

,

где — какие-то новые коэффициенты.

Осуществляя замену переменных , получим

.

Определитель матрицы этой квадратичной формы равен , а так как знак его совпадает со знаком , то , и, значит, квадратичная форма — положительно определена. Теорема доказана.

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы

была положительно определенной, а значит, чтобы все главные миноры матрицы

были положительны. Но это означает, что

т.е. что знаки главных миноров матрицы C чередуются, начиная со знака минус.

Пример. Вычислить, является ли квадратичная форма положительно (отрицательно) определенной или неопределенной.

а) .

Решение. Матрица квадратичной формы имеет вид:

.

Вычислим главные миноры матрицы С:

Квадратичная форма положительно определена.

б) .

Решение. Вычислим главные миноры матрицы

Квадратичная форма является неопределенной.

В заключение сформулируем следующую теорему.

Теорема (закон инерции квадратичных форм). Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится квадратичная форма невырожденными линейными преобразованиями, не зависит от выбора этих преобразований.

7.5. Задания для самостоятельной работы по главе 7

7.1. Доказать, что если квадратичная форма с матрицей А положительно определена, то и квадратичная форма с обратной матрицей положительно определена.

7.2. Найти нормальный вид в области вещественных чисел

.

7.3. Найти нормальный вид в области вещественных чисел

.

7.4. Найти нормальный вид в области вещественных чисел

.

7.5. Найти нормальный вид в области вещественных чисел

.

7.6. Найти нормальный вид в области вещественных чисел

7.7. Привести квадратичную форму к каноническому виду с целыми коэффициентами

.

7.8. Привести квадратичную форму к каноническому виду с целыми коэффициентами

.

7.9. Привести квадратичную форму к каноническому виду с целыми коэффициентами

.

7.10. Доказать, что в положительно определенной форме все коэффициенты при квадратах неизвестных положительны и что это условие не является достаточным для положительной определенности формы.

7.11. Выяснить, какие из форм эквивалентны между собой в области вещественных чисел

7.12. Выяснить, какие из форм эквивалентны между собой в области вещественных чисел

7.13. Найти все значения параметра , при которых квадратичная форма положительно определена

7.14. Найти все значения параметра , при которых квадратичная форма положительно определена

7.15. Найти все значения параметра , при которых квадратичная форма положительно определена

Источник

Содержание:

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Понятие квадратичной формы

Квадратичной формой

Пример:

Сумма 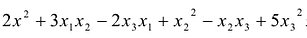является квадратичной формой от трех неизвестных .

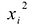
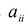
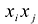
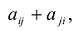
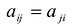
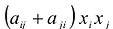
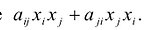
Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при обозначаются через а коэффициенты при через причем „ Член записывается в виде После этих преобразований квадратичную форму можно записать в виде:

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

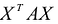
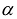
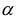
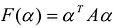
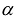
результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид . Если — произвольный n— мерный вектор, то после подстановки в квадратичную форму вместо X получится число , которое называется значением квадратичной формы F(X) на векторе .

Канонический базис квадратичной формы

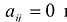
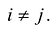
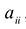
Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. при . При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами ,т.е.:

В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

где 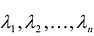-собственные значения матрицы А.

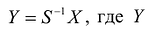
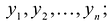
Применим к квадратичной форме линейное преобразование — матрица-столбец новых переменных — матрица, обратная к S.

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

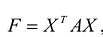
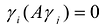
Базис пространства R» называется каноническим базисом квадратичной формы , если в этом базисе квадратичная форма имеет канонический вид, т.е. при

Если канонический базис F(X), то выражение: называется каноническим видом F(X) в базисе где — новый набор неизвестных.

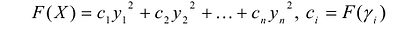
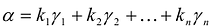
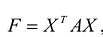
Теорема. Если — разложение вектора а по каноническому базису квадратичной формы то значение F(X) на векторе а вычисляется по формуле

Доказательство:

Эта теорема утверждает, что если известны канонический базис квадратичной формы F(X) и ее канонический вид в этом базисе, то для вычисления значения F(a) квадратичной формы F(X) на векторе а достаточно:

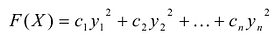
Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов симметрической матрицы , является каноническим базисом квадратичной формы , а выражение — ее каноническим видом в базисе ,

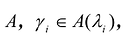
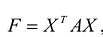
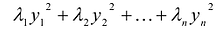
Доказательство:

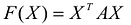
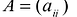
Канонический базис Якоби квадратичной формы . Будем говорить, что матрица удовлетворяет условию Якоби, если определители:

называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что

Обозначим через 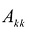матрицу:

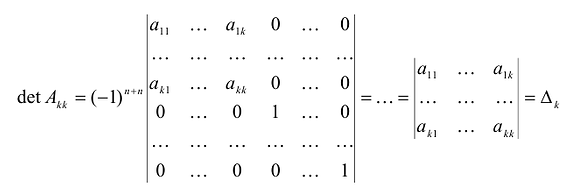
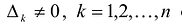
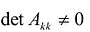
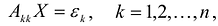
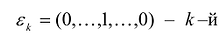
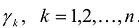
Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. Из условия следует, что и, значит, каждая система уравнений , где вектор диагональной системы, имеет единственное решение . Система векторов называется системой векторов Якоби матрицы А, которая удовлетворяет условию Якоби.

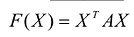
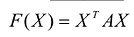
Теорема. матрица А квадратичной формы удовлетворяет условию Якоби, система векторов Якоби матрицы А является каноническим базисом квадратичной формы , а выражение:

ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник