какая прямая называется секущей какая касательной по отношению к окружности

Касательная и секущая к окружности

На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:

Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.

Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:

Касательная

Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:

Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.

Касательная – это прямая линия, имеющая с окружностью одну общую точку.

Секущая

Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:

Секущая – это прямая линия, имеющая с окружностью две общие точки.

Источник

Какая прямая называется секущей какая касательной по отношению к окружности

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Теорема о касательной и секущей

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

C = 2 R.

L = R .

S = R 2 .

Вписанные и описанные окружности

Окружность и треугольник

где S — площадь треугольника, а — полупериметр;

R = ,

R = ;

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a, S — площадь треугольника;

Окружность и четырехугольники

+ = + = 180°;

a + c = b + d ;

Касательная к окружности

1. Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол САО — прямой. Из треугольника АСО получим, что угол АОС равен 62 градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги АВ — тоже 62 градуса.

2. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

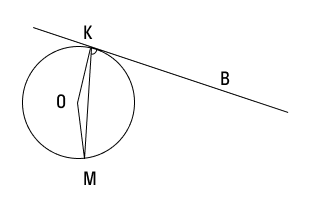
3. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Проведем радиус ОВ в точку касания, а также радиус ОА. Угол ОВС равен 90°. Треугольник ВОА — равнобедренный. Нетрудно найти, что угол ОВА равен 44 градуса, и тогда угол СВА равен 46 градусов, то есть половине угловой величины дуги АВ.

Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

4. Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Рассмотрите четырехугольник ОВСА. Сумма углов любого выпуклого четырехугольника равна 360°. Углы ОВА и ОВС и ОАС — прямые, угол ВОА равен 62°, значит, угол АСВ равен 28 градусов.

5. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника АВС складывается из периметров отсеченных треугольников.

Все эти задачи встречаются в Банке заданий ФИПИ под номером В6. А вот одна из сложных задач В3:

6. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку О — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку О с вершинами А, В, С, D, E. Получились треугольники АОВ, ВОС, СОD, DOE и ЕОА.
Очевидно, что площадь многоугольника S = S_АОВ + S_ВОС + S_СОD + S_DOE + S_ЕОА.
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?

Источник

Хорда, секущая, касательная

Определения

Хорда – отрезок, соединяющий две точки окружности.

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

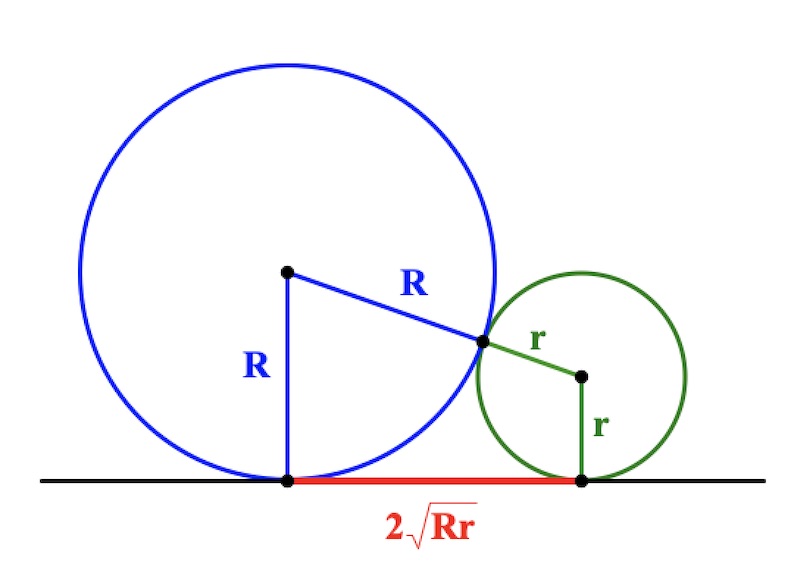
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Касательная к окружности

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

Докажем, что касательная и радиус АВ перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

Поскольку ∠АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, ⌒АВ = 62°.

Если провести две касательных к окружности из одной точки, то их отрезки от этой начальной точки до точки касания будут равны.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично должны быть равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

sin BDA = AB : AD = 4,5 : 9 = 0,5

Мы знаем, что прямая, проложенная из точки до центра окружности, делит угол между касательными, проложенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN между ними равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности опускаются две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

Сократим уравнение на (у + R) и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ ⌒АВ.

⌒АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

⌒КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

• ← Как сделать лизинг своими руками
• Как сделать макияж глаз стойким →