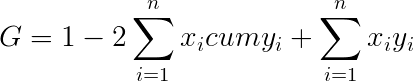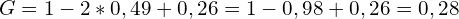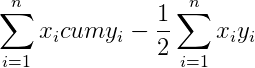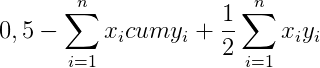какие факторы оказывают влияние на форму кривой лоренца
Доходы населения, кривая Лоренца
Вы будете перенаправлены на Автор24
Дифференциация доходов
На изменение доходов населения оказывают влияние различные факторы, которые воздействуют с неодинаковой силой и в разном направлении.
Размер доходов и различия в их уровне обусловлены влиянием таких факторов, как:
Рассмотрим подробнее каждый из перечисленных факторов.
При переходе к рыночной экономике изменяются социальные взгляды общества, что обуславливает перемены в трудовой, правовой, финансовой, инвестиционной, социально-бытовой, технической и других сферах жизнедеятельности общества. Поскольку основой рыночной экономики является конкуренция, то она воздействует на формирование доходов компаний, а, следовательно, и на доходы отдельных работников. При переходе к рыночной системе хозяйствования на начальной стадии в некоторой степени выравниваются трудовые доходы предприятий с одинаковыми технико-экономическими показателями. На сегодняшний день занятость населения зависит не только от личной инициативы, но и во многом от государственной социальной политики в сфере регулирования трудового рынка. Таким образом, при формировании доходов населения направленность и силу влияния других факторов в значительной степени определяют социально-политические факторы.
При рассмотрении социально-демографических факторов следует уделять внимание формированию доходов различных групп населения, поскольку различия по возрасту, полу существенно влияют на доходы.
Большое значение имеют процессе формирования доходов и их дифференциации социально-профессиональные факторы, так как различные специальности требуют различного уровня образования, профессионализма, опыта. Заработок трудящихся во многих случаях зависит от квалификации.
С описанными выше факторами тесно взаимосвязаны социально-статусные факторы, которые во многом и определяются ими. Для каждого социального статуса человека характерно определенное место в обществе и соответствующие возможности получения дохода.
В значительной степени на размеры и структуру доходов влияют социально-экономические факторы, которые не представляется возможным реализовать без других факторов. В данном случае на доходы оказывают влияние род и вид деятельности, варианты занятости, виды производства, формы собственности, условия труда и др.
Готовые работы на аналогичную тему
Социально-географические факторы определяются природно-климатическими условиями, территориальным пространством, характером распределения населения на территории страны.
На формирование доходов воздействуют факторы трех уровней:
Таким образом, на дифференциацию доходов оказывают влияние многочисленные и разнообразные факторы. Грамотное управление данными факторами на каждом уровне позволяет рационально регулировать доходы населения и воздействовать на улучшение уровня жизни.
Кривая Лоренца
Под доходами понимается сумма денежных средств, которая получена за определенный временной промежуток и предназначена для покупки товаров и услуг с целью личного потребления.
Чтобы оценить уровень и динамику доходов применяются такие показатели:
Реальный доход, который определяется по формуле:
Источниками доходов могут быть:
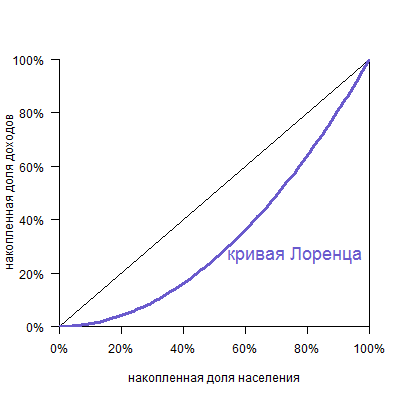
При определении неравенства доходов в большинстве случаев применяется кривая Лоренца (рисунок 1), построение которой происходит следующим образом: на горизонтальной оси отображается процент групп населения, которые располагают определенными доходами, а на вертикальной – проценты доходов, которые получают данные группы.
Рисунок 1. Кривая Лоренца. Автор24 – интернет-биржа студенческих работ
При помощи кривой Лоренца можно определить неравенство при распределении доходов, степень различия равного распределения доходов и фактического распределения, т.е. биссектрисой и кривой Лоренца. Чем больше отклонение кривой Лоренца от биссектрисы, тем большая степень неравенства доходов.
Социальная политика государства и социальные трансферты
Политика государства в области доходов заключается в процессе перераспределения доходной части через бюджет государства при помощи дифференцированного налогообложения и социальных трансфертов. При этом немалая доля национальных доходов переходит от богатых слоев населения к бедным. На сегодняшний день во всех развитых странах создана система социальной поддержки малообеспеченных.
Под социальными трансфертами понимается система мер по натуральной или денежной помощи малообеспеченными, не связанная с их привлечением к хозяйственной деятельности. Население может получать выплаты из местного бюджета, государственных внебюджетных фондов социального обеспечения, а также за счет средств различных общественных организаций.
К социальным трансфертам относятся:
Социальными трансфертами в натуральной форме могут быть индивидуальные товары и услуги, предоставляемые населению безвозмездно или же по льготной стоимости.
Государственная социальная политика призвана решать такие задачи:
Кривая Лоренца
Кривая Лоренца (Lorenz curve) — график, демонстрирующий степень неравенства в распределении дохода в обществе, отрасли, а также степени неравенства в распределении богатства. Если обратиться к кривой Лоренца показывающей степень неравенства в распределении дохода в обществе, то график или кривая Лоренца будет отражать долю дохода, приходящуюся на различные группы населения сформированные на основании размера дохода, который они получают.
Неравенство доходов в конце XIX — начале XX века стало объектом изучения многих экономистов США и Западной Европы. Центральной проблемой изучения является оценка справедливости и эффективности сложившегося в рыночной экономике распределения доходов и богатства. В 1905 году американский статистик Макс Лоренц разработал метод оценки распределения доходов, получивший название кривой Лоренца.
На оси абсцисс откладывается доля населения, а на оси ординат — доля доходов в обществе в процентном отношении. Как видно из графика, в обществе всегда имеет место быть неравенство в распределении доходов, что отражает кривая \mathrm
Если бы в обществе было бы равное распредение дохода, то кривая Лоренца приняла бы вид прямой (биссектриса на графике), называемая линией абсолютного равенства, и, наконец, если бы в обществе весь доход получали только 1% населения, то на графике это выразилось бы вертикальной прямой линией, называемой линией абсолютного неравенства.
На основании кривой Лоренца можно вывести коэффициент Джинни.
14.2 Кривая Лоренца и коэффициент Джини
Кривая Лоренца отражает кумулятивные (накопленные) доли дохода населения. Построение кривой Лоренца удобнее всего рассмотреть на следующем примере:
Представим экономику, состоящую из 3-х агентов: А, B, C. Доход агента А составляет 200 единиц, доход агента В составляет 300 единиц, доход агента С составляет 500 единиц.
Для построения кривой Лоренца найдем доли индивидов в общем доходе. Общий доход составляет 1000. Тогда доля индивида А составляет 20%, доля В составляет 30%, доля С составляет 50%.
Далее будем искать кумулятивные (накопленные) доли доходов и численности населения для индивидов, начав с самого бедного и постепенно включая более богатых индивидов:
Доля в населении индивида А составляет 33%. Доля его дохода составляет 20%.
Затем включим в анализ более богатого индивида – индивида В.
Совместная доля А+В в населении составляет 67%. Совместная доля А+В в доходе составляет 50% (20%+30%).
Далее включим в анализ еще более богатого индивида С.
Совместная доля А+В+С в населении составляет 100%. Совместная доля А+В+С в доходе составляет 100% (20%+30%+50%).
Отметим полученные результаты на графике:
Линия, соединяющая левую нижнюю точку и правую верхнюю точку графика, называется линией равномерного распределения доходов. Это гипотетическая линия, которая показывает, что было бы, если доходы в экономике распределяются равномерно. При неравномерном распределении доходов кривая Лоренца лежит левее этой линии, причем чем больше степень неравенства, тем сильнее изгиб кривой Лоренца. А чем ниже степень неравенства, тем более она приближена к линии абсолютного равенства.
В нашем случае кривая Лоренца выглядит как кусочно-линейный график. Это получилось так, потому что в нашем анализе мы выделили только три группы населения. С ростом числа рассматриваемых групп населения кривая Лоренца будет выглядеть следующим образом:
Кривая Лоренца позволяет судить о степени неравенства доходов в экономике о ее изгибу. Для количественного измерения степени неравенства дохода по кривой Лоренца существует специальный коэффициент – коэффициент Джини.
Коэффициент Джини равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника под кривой Лоренца.
если кривая Лоренца изображена не в %, а в долях, то площадь большого треугольника всегда равна ½. Формула коэффициента Джини для этого случая приобретает вид:
Коэффициент Джини может принимать значения от 0 до 1. Чем ближе коэффициент Джини к нулю, тем меньше изгиб кривой Лоренца, и доходы распределены более равномерно. Чем ближе коэффициент Джини к единице, тем больше изгиб кривой Лоренца, и доходы распределены менее равномерно.
Площадь внутренней фигуры D быстрее всего можно посчитать путем вычитания из площади большого треугольника площади фигур А, В и С.
В этом случае коэффициент Джини будет равен:
Частный случай кривой Лоренца и коэффициента Джини: попарное сравнение.
Материалы данного раздела не публикуются на сайте, а доступны в полной версии данного пособия, которое я использую на занятиях с учениками.
Как известно, любой статистический показатель имеет свои изъяны. Так же как и по показателю ВВП нельзя судить об уровне благосостояния экономики, и коэффициент Джини (и другие показатели степени неравенства) не могут дать в полной мере объективную картину степени неравенства доходов в экономике.
Это происходит по нескольким причинам:
Данные показатели используются для оценки степени неравенства доходов, и входят в область позитивного экономического анализа. Напомним, что позитивный анализ отличается от нормативного анализа тем, что позитивный анализ анализирует экономику объективно, как есть, а нормативный анализ является попыткой улучшить мир, сделать «как должно быть». Если оценка степени неравенства является позитивным экономическим анализом, то попытки снизить неравенство в распределении доходов принадлежат к области нормативного экономического анализа.
Нормативный экономический анализ известен тем, что разные экономисты могут предложить разное, часто диаметральное противоположные рекомендации по решению одной и той же проблемы. Это не означает, что кто-то является более компетентным, а кто менее компетентным. Это только означает, что экономисты отталкиваются от различных философских взглядов на понятие справедливости, а единства в этом вопросе нет.
Сначала мы рассмотрим различные существующие системы ценностей, а затем покажем, каким образом можно обеспечить более справедливое распределение доходов в рамках каждой системы.
Материалы данного раздела не публикуются на сайте, а доступны в полной версии данного пособия, которое я использую на занятиях с учениками.
Налоги и налоговая система
Про экономику США XIX века можно сказать, что она была идеальным примером свободного капитализма. Идеалы Адама Смита о минимальном вмешательстве государства в распределение ресурсов и функционирование рынков (вспомним знаменитый принцип laissez faire) были взяты на вооружение в то время, вмешательство государство в рынок было минимальным, государственные расходы составлял 7-8% от совокупных расходов, а средняя ставка налогообложения для граждан США составляла 5% от доходов. Весь XX век прошел под знаменем активного наращивания присутствия государства в экономике, государственные расходы выросли до 25%-30% от совокупных расходов, а средняя ставка налогообложения выросла до 35% от доходов.
Государство сейчас выступает не только в качестве устранителя рыночных провалов, о которых мы активно говорили в прошлой главе (внешние эффекты и предоставление общественных благ), но и в качестве стимулятора экономики, когда экономика испытывает трудные времена.
Налоги являются основным источником доходов государства. Любое государство имеет множество налогов и сборов, построенных по определенным принципам, а также институты контроля по сбору налогов. Все это составляет налоговую систему государства.
Для оценки налоговой системы используются принципы эффективности и справедливости. Как мы уже знаем, понятие справедливости не является точно определённым для экономистов. В зависимости от системы моральных ценностей справедливость может быть установлена тем или иным образом. Экономисты гораздо более едины при определении того, что такое эффективность. Эффективной является та налоговая система, которая менее всего приводит к искажению стимулов у участников рынка, а следовательно, и к возникновению безвозвратных потерь.
Покажем, каким образом безвозвратные потери связаны с искажением стимулов у участников рынка.
По теме «рыночное равновесие» мы помним, что безвозвратные потери возникали, когда налоги и субсидии изменяли положение кривых спроса и предложения, то есть изменяли экономическое поведение людей. Безвозвратные потери заключались в том, что какие-то покупатели не смогли купить товар, а какие-то производители не могли продать товар по сравнению с ситуацией, когда цены точно отражают предельные издержки.
Таким же образом любые налоги приводят к безвозвратным потерям, поэтому можно смело утверждать, что любые налоги неэффективны в этом смысле. Задача экономистов заключается в том, чтобы найти такие налоги, которые будут минимально искажать стимулы людей, а значит, и приводить к минимальным безвозвратным потерям.
Налоги могут взиматься по-разному в зависимости от величины дохода. Для того, чтобы оказать это, нам будут нужны два типа налоговых ставок: средняя налоговая ставка и предельная налоговая ставка.
Средняя налоговая ставка показывает, какой % налога в среднем платит индивид с полученного дохода
Предельная налоговая ставка показывает, какой % налога платит индивид с дополнительного дохода:
Средняя и предельная ставки ведут себя также, как и любые средние и предельные величины:
В зависимости от поведения средней и предельной ставки налога выделяют 3 вида налогов: прогрессивные, пропорциональные, регрессивные.
У прогрессивного налога средняя ставка налога растет по мере увеличения дохода, а значит, предельная налоговая ставка превышают среднюю.
Примеры прогрессивных налогов: налоги на доходы во Франции, налоги в Швеции, автомобильный налог в России.
У пропорционального налога средняя ставка не изменяется с ростом дохода, а значит, средняя налоговая ставка совпадает с предельной.
Примеры пропорциональных налогов: подоходный налог в России 13%, налог на прибыль в России 20%.
В случае, если индивиду предложена одинаковая налоговая ставка при существовании некоего налогонеоблагаемого минимума (или же предоставлен налоговый вычет), то данная налоговая система является уже не пропорциональной, а прогрессивной. Индивид сначала вообще не платит налогов, а потом, после превышения налогонеоблагаемого минимума, начинает платить налог по одинаковой ставке.
У регрессивных налогов средняя ставка падает с ростом дохода, а значит, предельная ставка налога оказывается ниже средней.
Другие примеры регрессивных налогов – это любые фиксированные налоги и пошлины. Например, в РФ человек вынужден заплатить фиксированную пошлину в размере около 1000 рублей при регистрации номерного знака автомобиля. Данный вид налога является регрессивным, поскольку пошлина оставляет большую часть дохода для бедного человека, и меньшую часть дохода для богатого человека.
Какой из данных видов налогов является более справедливым? Популярной является точка зрения, что прогрессивные налоги являются более справедливыми, а регрессивные менее справедливыми. Но эта точка зрения ошибочна. Как мы показали раньше, все зависит от того, в рамках какой системы моральных ценностей мы будем говорить о справедливости.
Рассмотрим простой пример. Индивид А получает доход 10 рублей и платит налог по ставке 10%. Индивид В получает доход 90 рублей и платит налог по ставке 5%. Налоговая шкала является регрессивной – средняя ставка падает при росте дохода. Но является ли она несправедливой? Посчитаем сумму налога, уплаченную каждым индивидом. Индивид А платит 1 рубль (=10*10%), индивид В платит 4.5 рубля (=90*5%). В результате индивид, зарабатывающий больше, платит и большую сумму налога. И в чем же здесь несправедливость?
Для оценки справедливости налоговой системы выделяются следующие постулаты:
В зависимости от того, каким образом налоги собираются в государственный бюджет, различают прямые и косвенные налоги.
Прямые налоги – это налоги, которые уплачивает тот, кто является носителем налога. Например, налог на прибыль является прямым налогом, потому что его оплачивает фирма, которая получает эту прибыль. Подоходный налог является прямым налогом, поскольку его уплачивает индивид, который получает налогооблагаемый доход.
Косвенные налоги – это налоги, которые уплачивает тот, кто не является носителем налога. Например, акцизы на алкоголь и сигареты уплачивают фирмы. Однако носителем налога в этом случае является потребитель, потому что акцизы «сидят» в цене товаров, покупаемых потребителем. Косвенными налогами в России являются НДС (налог на добавленную стоимость) и акцизы. Все косвенные налоги являются регрессивными по отношению к доходам покупателей.
Какие налоги являются более популярными: прямые или косвенные? Ответ заключается в том, что косвенные налоги легче собрать, поскольку фактически они вводятся на расходы потребителей. Прямые налоги собрать тяжелее, потому что они вводятся преимущественно на доходы, и в этом случае индивиды имеют стимулы к уклонению от налогов путем сокрытия доходов. Поэтому косвенные налоги более популярны в государствах с неразвитыми институтами, где индивиды могут и хотят уклоняться от налогов.
Еще одним эффектом, который оказывают прямые или косвенные налоги на экономику, являются стимулы индивидов к сбережениям. Прямые налоги обычно вводятся на текущие доходы индивидов, поэтому индивиды не имеют стимулов делать большие сбережения. Косвенные налоги стимулируют индивидов к сбережениям, потому что эти налоги вводятся на потребление. Сберегая деньги, а не тратя их в настоящий момент, индивиды платят меньше налогов сейчас при косвенных налогах, и платят больше налогов сейчас при прямых налогах.
Влияние налогов на неравенство доходов
Материалы данного раздела не публикуются на сайте, а доступны в полной версии данного пособия, которое я использую на занятиях с учениками.
1 Можно считать коэффициент Джини для кривой Лоренца в %, просто расчеты будут более громоздкими.
Как рассчитывать коэффициент Джини
Автор: Игорь Святославович Демин · Опубликовано 21.11.2017 · Обновлено 19.01.2021
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
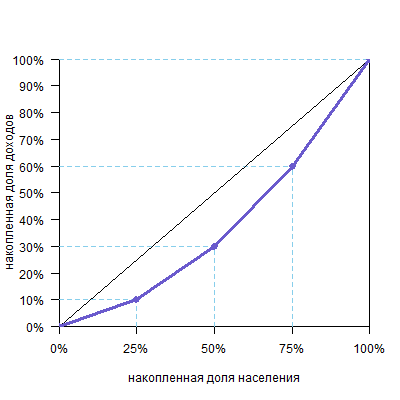
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
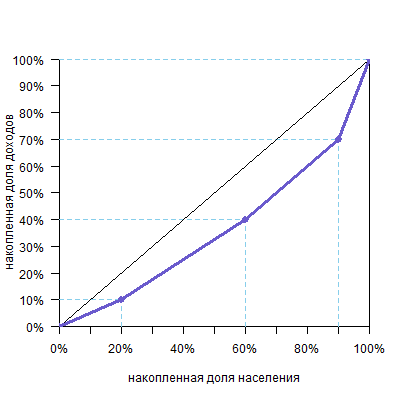
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
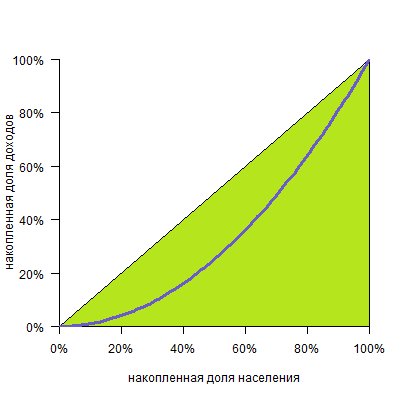
Получим такой график:
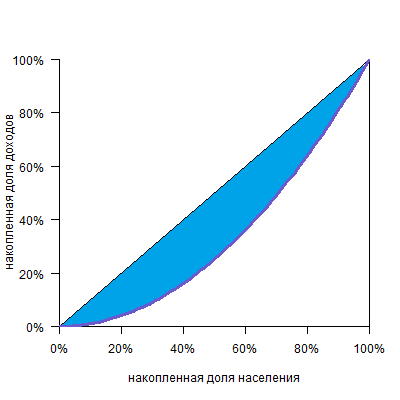
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
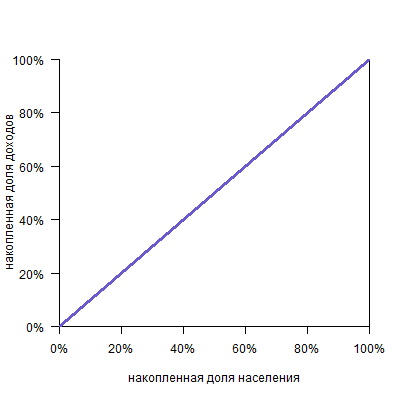
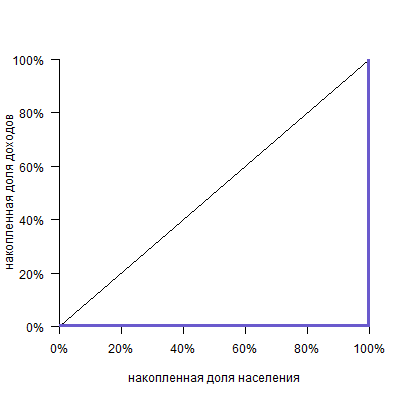
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
К площади треугольника под диагональю (а она всегда равна 0,5):
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
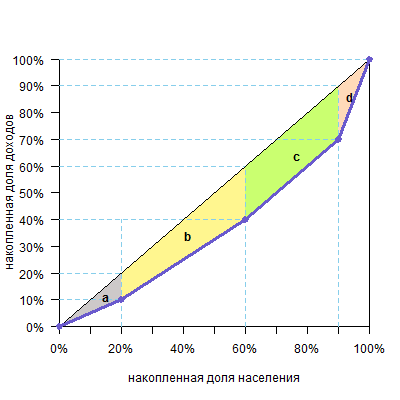
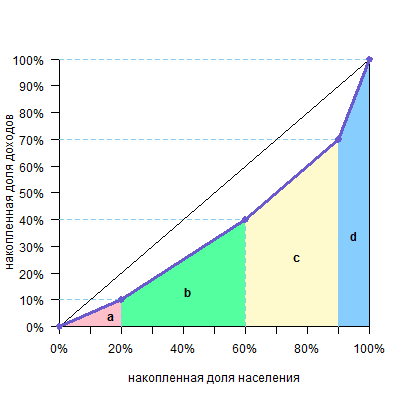
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
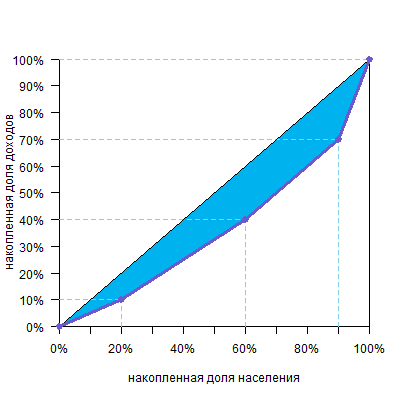
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:
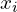
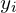
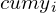
Составим таблицу на основе данных предыдущего примера:
| Доля населения ( 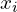 ) ) | Доля от общего дохода ( 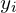 ) ) | Накопленная доля общего дохода ( 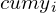 ) ) | 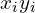 | 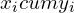 |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Как построена эта таблица
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
Как выведена эта формула?
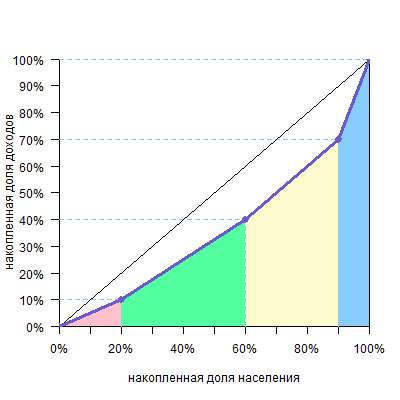
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
можно сперва посчитать площадь фигуры под кривой Лоренца
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
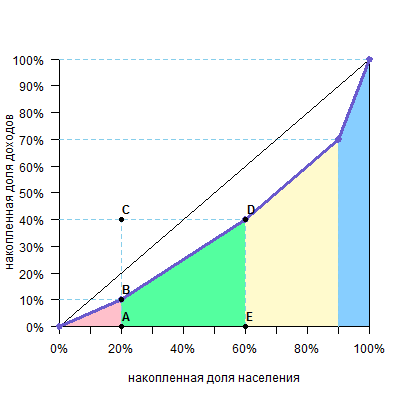
Рассмотрим, например, вторую группу (зеленый четырехугольник).
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.\