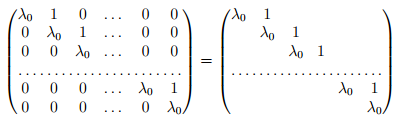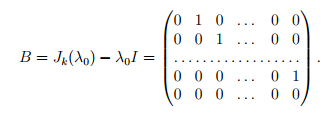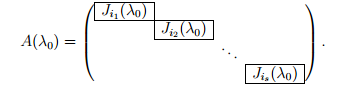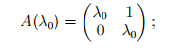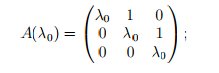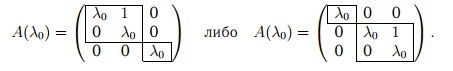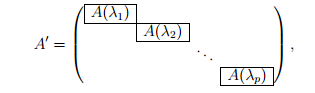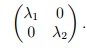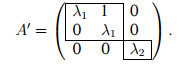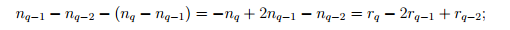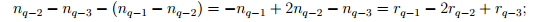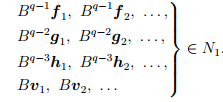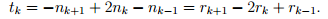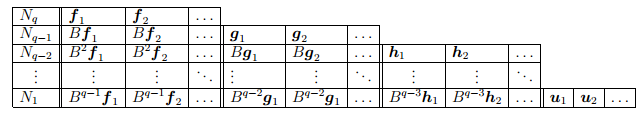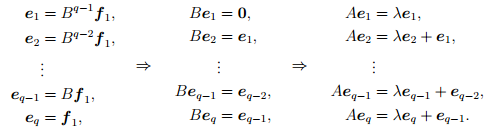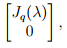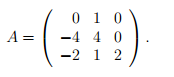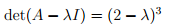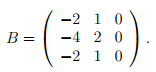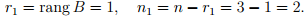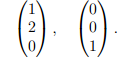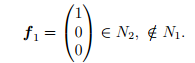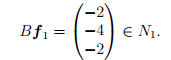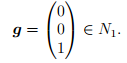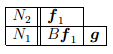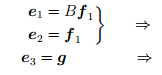какие матрицы можно привести к жордановой форме

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Жорданова нормальная форма

Жорданова нормальная форма над полем комплексных чисел

Общая схема

Аннулирующий полином

Теорема 5. Минимальный аннулирующий полином оператора является делителем его характеристического полинома. Два минимальных аннулирующих полинома оператора различаются, разве лишь, постоянным множителем.

Следствиями теорем 4 и 5 является следующий результат.

Корневое подпространство

Рассмотрим теперь пример, разобранный в ☞ ПУНКТЕ.

Пример 3. Найти корневые векторы матрицы

Доказательство. Следствие теоремы 2. ♦

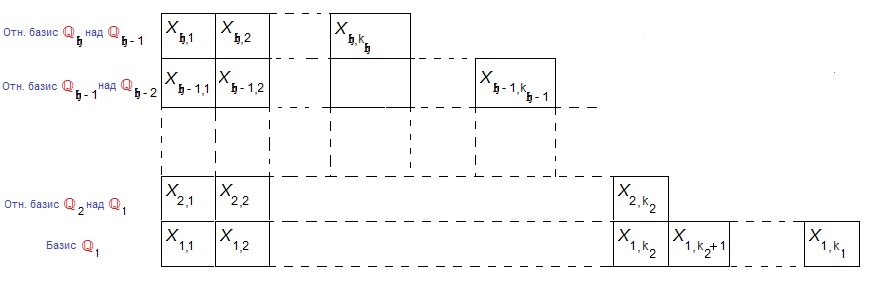
Алгоритм построения базиса корневого подпространства

Для визуализации последующего алгоритма построения канонического базиса удобно представить результаты этого этапа в виде схемы:

Мы наблюдаем разноэтажное здание, число квартир на каждом этаже которого не превосходит числа квартир на предыдущем. В ходе дальнейшего алгоритма, часть «жильцов» останется на месте, а часть может быть замещена другими.

4. Продолжаем процесс…

Структура соответствующего канонического базиса

В каноническом базисе корневые векторы, соответствующие указанной последовательности клеток, следует упорядочить по следующему правилу:

Объяснение необходимости перестановки векторов канонического базиса — почему они нумеруются по правилу «сверху вниз», а не поэтажно — дается в следующем ПУНКТЕ.

Пример 3 (окончание). Построить ЖНФ и канонический базис пространства для оператора из примера 3.

Циклическое подпространство

Построить ЖНФ и канонический базис для оператора из примера 2.

Жорданова нормальная форма над полем вещественных чисел

Источник

Жорданова нормальная форма матрицы оператора, жорданов базис.

Материал для изучения нормальной жордановой формы матрицы и жорданова базиза. Работа содержит теоретический материал, теоремы и примеры.

Просмотр содержимого документа
«Жорданова нормальная форма матрицы оператора, жорданов базис.»

Жорданова нормальная форма матрицы оператора, жорданов базис.

Определения и основные понятия

Введем два основных понятия.

1.1 Жорданова клетка

Жордановой клеткой порядка k, относящейся к числу λ₀, называется матрица порядка k, 1≤k≤n, имеющая вид:

Также можем сказать, что на её главной диагонали стоит одно и то же число из поля P, а параллельные элементы, ближайшие к главной диагонали сверху, равны 1, все остальные элементы матрицы равны нулю.

Её характеристический многочлен (λ₀ − λ) k имеет корень λ₀ кратности k.

Таким образом, данная матрица имеет собственное значение λ₀ алгебраической кратности k. Отвечающие ему собственные векторы — это ненулевые решения однородной системы линейных уравнений с матрицей

Так как rangB = k −1, так что размерность собственного подпространства равна 1, то существует лишь один линейно независимый собственный вектор. Таким образом, при k ≥ 2 не существует базиса, состоящего из собственных векторов этого оператора, то есть ни в одном базисе матрица оператора не может иметь диагонального вида. Матрица J_k(λ₀) называется жордановой клеткой порядка k, соответствующей собственному значению λ₀.

Жордановым блоком, отвечающим собственному значению λ₀, называется блочно-диагональная матрица, каждый блок которой представляет собой жорданову клетку вида:

Все элементы матрицы вне жордановых клеток равны нулю. Порядок расположения жордановых клеток в матрице A(λ₀) определен неоднозначно.

1.3 Примеры жордановых блоков

Рассмотрим простой случай, когда характеристический многочлен матрицы имеет вид f(λ) = (λ₀ − λ) m и геометрическая кратность собственного значения λ₀ равна s.

Пример 1. Пусть m = 2, s = 1. Тогда

имеем одну жорданову клетку порядка 2.

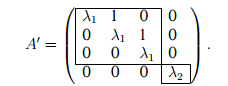
Пример 2. Пусть m = 3, s = 1. Тогда

имеем одну жорданову клетку порядка 3.

Пример 3. Пусть m = 3, s = 2. Имеем жорданов блок, состоящий из двух жордановых клеток порядков 1 и 2:

Теорема о жордановой форме матрицы оператора

Пусть линейный оператор A действует в линейном пространстве над полем комплексных чисел размерности n и его характеристический многочлен имеет вид

Тогда в этом пространстве существует базис, состоящий из собственных и присоединенных векторов оператора A, в котором матрица оператора имеет блочно-диагональную форму (она называется жордановой формой)

где A(λ_j ) — жорданов блок, соответствующий собственному значению λ_j. Указанный базис называется жордановым.

Сформулированная теорема верна и в случае, когда линейный оператор действует в линейном пространстве над произвольным числовым полем K, но все корни характеристического многочлена принадлежат полю K.

Рассмотрим примеры. Обозначаем через n размерность пространства, m_j и s_j — алгебраическую и геометрическую кратности собственного значения λ_j соответственно.

Пример 1. Пусть n = 2, λ₁ ≠ λ₂. Тогда матрица оператора может быть приведена к диагональному виду:

Базис векторного пространства, в котором матрица оператора имеет вид одной сплошной ячейки, должен обладать свойством («цикличность»), которое получим на основе правила «столбцы матрицы = образы базисных векторов».

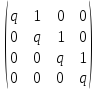
Здесь q обозначает некое, известное нам число.

Это означает, что координаты вектора e₁ в этом базисе равны (1,0,0,0).

Как нетрудно проверить, верно и обратное: если первый базисный вектор является по совместительству собственным вектором оператора с собственным числом q, то первый столбец матрицы оператора в таком базисе равен (q,0,0,0).

Теперь займемся вторым базисным вектором e₂. Его координаты равны (0,1,0,0). Умножив на столбец (0,1,0,0) нашу матрицу, мы получим в качестве результата ее второй столбец (1,q,0,0). Это означает, что

Точно так же получаются равенства

В итоге мы приходим к выводу: если матрица оператора A в некотором базисе имеет вид Жордановой клетки (ячейки) с числом q на диагонали и с единичкам над ней, то векторы базиса превращаются друг в друга под воздействием оператора B=A-qE:

В этой цепочке стрелки (слева направо) показывают, что из каждого базисного вектора получается под воздействием оператора B.

4 Построение жорданова базиса и жордановой формы матрицы

Пусть λ — собственное значение оператора, m и s — алгебраическая и геометрическая кратности числа λ. Опишем построение линейно независимой совокупности из m собственных и присоединенных векторов, отвечающих данному λ. Этой совокупности векторов в жордановой матрице A′ будет соответствовать жорданов блок A(λ).

Теорема. Существует такое натуральное число q, что

т.е. все ядра с номером, большим, чем q, совпадают с ядром N_q. При этом

Построим часть жорданова базиса, соответствующую данному собственному значению λ, следующим образом.

1. Возводя матрицу B в последовательные натуральные степени, найдем показатель q, начиная с которого ранг степеней матрицы B перестает уменьшаться.

таким же будет количество жордановых клеток порядка q − 1.

таким же будет количество жордановых клеток порядка q − 2.

Процесс продолжаем аналогично. Наконец, рассмотрим ядро N₁ и векторы

Итак, мы описали процесс построения жорданова базиса и выяснили, что количество жордановых клеток порядка k, входящих в состав жордановой формы матрицы оператора, может быть найдено по формуле

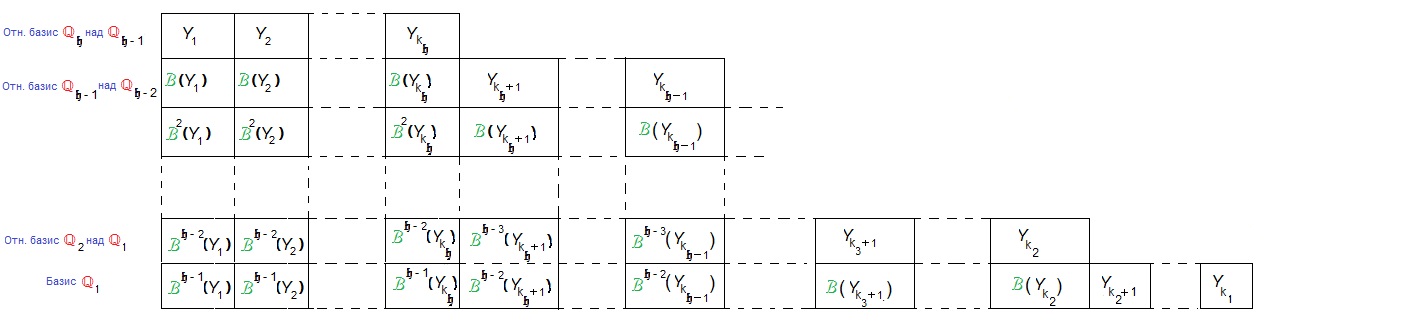
Построенную часть жорданова базиса, состоящую из m векторов, соответствующих данному λ (m — алгебраическая кратность этого собственного значения), запишем в таблицу («жорданова лестница»):

Все векторы таблицы линейно независимы, и их число равно m (алгебраической кратности собственного значения λ). Каждому столбцу этой таблицы соответствует одна жорданова клетка, порядок которой равен высоте столбца. Количество столбцов жордановой лестницы, т.е. полное количество жордановых клеток в блоке, соответствующем собственному значению λ, равно геометрической кратности s этого собственного значения.

Будем нумеровать векторы построенной части базиса по столбцам жордановой лестницы: внутри каждого столбца снизу вверх, а сами столбцы в произвольном порядке.

где J_q(λ) — жорданова клетка порядка q с числом λ на главной диагонали.

В следующих q столбцах матрицы A′, определенных векторами второго столбца жордановой лестницы, расположена жорданова клетка J_q(λ) так, что числа λ стоят на главной диагонали матрицы A′, а элементы вне клетки равны нулю. Подобным образом для данного λ получаем m столбцов матрицы A′. На этих m столбцах находится жорданов блок A(λ).

Для других собственных значений эта схема повторяется, в результате чего получим жорданову матрицу A′ и соответствующий жорданов базис.

4.1 Пример решения задач

Дана матрица A линейного оператора в некотором базисе. Требуется найти жорданов базис и жорданову форму матрицы оператора в этом жордановом базисе. Рассмотрим пример решения такой задачи методом построения жорданова базиса.

имеет корень λ = 2 кратности 3, т.е. m = 3. Матрица B = A − λI равна

Легко проверить, что

Собственные векторы находим, решив однородную систему линейных уравнений BX = O; фундаментальная совокупность решений состоит из двух векторов, например,

Количество этих векторов (т.е. геометрическая кратность собственного значения) равно двум, s = 2, так что для построения жорданова базиса требуется еще один присоединенный вектор.

Дополним базис ядра N₁, т.е. набор векторов (2), до базиса ядра N₂, например, вектором

Построим жорданову лестницу:

соответствует жорданова клетка порядка 2,

Источник

СОДЕРЖАНИЕ

Обзор

Обозначение

В некоторых учебниках есть поддиагональ ; то есть непосредственно под главной диагональю, а не на наддиагонали. Собственные значения по-прежнему находятся на главной диагонали.

Мотивация

Комплексные матрицы

где каждый блок J _i представляет собой квадратную матрицу вида

Предполагая этот результат, мы можем вывести следующие свойства:

Пример

Пример: получение нормальной формы

В этом примере показано, как вычислить нормальную форму Жордана данной матрицы.

о котором упоминается в начале статьи.

Вычисление показывает, что уравнение P −1 AP = J действительно выполняется.

Обобщенные собственные векторы

Доказательство

В противном случае, если

Уникальность

Можно показать, что жорданова нормальная форма данной матрицы A единственна с точностью до порядка жордановых клеток.

равно удвоенному количеству жордановых блоков размера k ₁ плюс количество жордановых блоков размера k ₁ −1. Общий случай аналогичен.

Реальные матрицы

и описать умножение на в комплексной плоскости. Наддиагональные блоки представляют собой единичные матрицы 2 × 2 и, следовательно, в этом представлении размерности матрицы больше, чем у комплексной жордановой формы. Полный реальный блок Джордана дается формулой λ я <\ displaystyle \ lambda _ >

Эта вещественная жорданова форма является следствием комплексной жордановой формы. Для действительной матрицы невещественные собственные векторы и обобщенные собственные векторы всегда можно выбрать для образования комплексно сопряженных пар. Взяв действительную и мнимую части (линейную комбинацию вектора и сопряженного с ним), матрица имеет такой вид относительно нового базиса.

Матрицы с записями в поле

Последствия

Можно видеть, что нормальная форма Жордана является, по сути, результатом классификации квадратных матриц, и поэтому несколько важных результатов линейной алгебры можно рассматривать как ее следствия.

Теорема о спектральном отображении

Характеристический полином

Теорема Кэли – Гамильтона

Минимальный многочлен

Инвариантные разложения подпространств

Можно также получить несколько иное разложение с помощью жордановой формы. Для заданного собственного значения λ _i размер его наибольшего соответствующего жорданова блока s _i называется индексом λ _i и обозначается ν (λ _i ). (Следовательно, степень минимального многочлена равна сумме всех индексов.) Определим подпространство Y _{i следующим} образом:

Это дает разложение

Здесь может быть интересно отметить некоторые свойства индекса ν ( λ ). В более общем смысле, для комплексного числа λ его индекс может быть определен как наименьшее неотрицательное целое число ν (λ) такое, что

Плоская (плоская) нормальная форма

Жорданова форма используется для нахождения нормальной формы матриц с точностью до сопряжения, такой что нормальные матрицы составляют алгебраическое многообразие низкой фиксированной степени в пространстве объемлющих матриц.

Множества представителей классов матричной сопряженности для жордановой нормальной формы или рациональных канонических форм в общем случае не составляют линейных или аффинных подпространств в объемных матричных пространствах.

Для алгебраически замкнутых полей она была решена Петерисом Даугулисом. Построение однозначно определенной плоской нормальной формы матрицы начинается с рассмотрения ее жордановой нормальной формы.

Матричные функции

Итерация цепочки Джордана мотивирует различные расширения к более абстрактным параметрам. Для конечных матриц получаются матричные функции; это может быть распространено на компактные операторы и голоморфное функциональное исчисление, как описано ниже.

В следующем примере показано приложение к степенной функции f ( z ) = z n :

Компактные операторы

Голоморфное функциональное исчисление

Нам потребуются следующие свойства этого функционального исчисления:

Конечномерный случай

Теорема о спектральном отображении говорит нам

имеет спектр <0>. По свойству 1 f ( T ) может быть непосредственно вычислено в жордановой форме, и, проверив, мы видим, что оператор f ( T ) e _i ( T ) является нулевой матрицей.

Поляки оператора

Точка λ называется полюсом оператора T порядка ν, если резольвентная функция R _T, определенная равенством

имеет полюс порядка ν в точке λ.

Мы покажем, что в конечномерном случае порядок собственного значения совпадает с его индексом. Результат верен и для компактных операторов.

Согласно предыдущему обсуждению функционального исчисления,

Но мы показали, что наименьшее натуральное число m такое, что

в точности индекс λ, ν (λ). Другими словами, функция R _T имеет полюс порядка ν (λ) в точке λ.

Числовой анализ

Если матрица A имеет несколько собственных значений или близка к матрице с несколькими собственными значениями, то ее жорданова нормальная форма очень чувствительна к возмущениям. Рассмотрим, например, матрицу

Если ε = 0, то нормальная форма Жордана просто

Однако при ε ≠ 0 жорданова нормальная форма имеет вид

Источник