какие многогранники представляют собой простые формы

Какие многогранники представляют собой простые формы

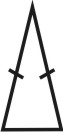
Кратко охарактеризуем геометрические свойства некоторых многогранников:

а) модель		б) эпюр
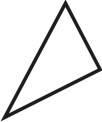
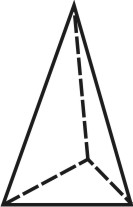
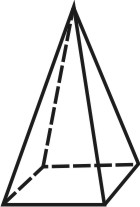
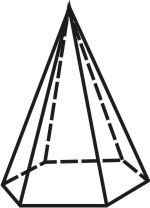
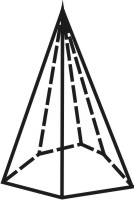
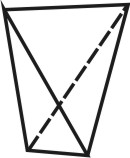
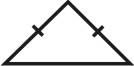
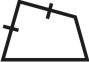
Рисунок 67. Пирамида

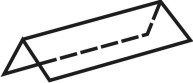
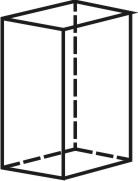
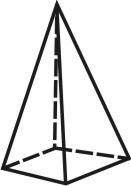
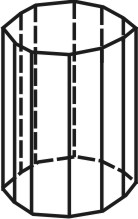
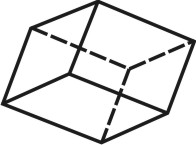
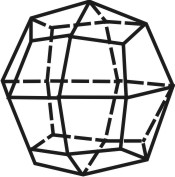
2. Призма — многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
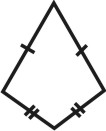
Рисунок 68. Призма

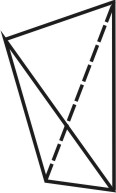
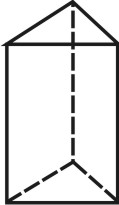
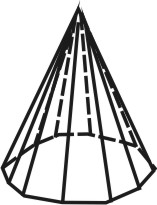
3. Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

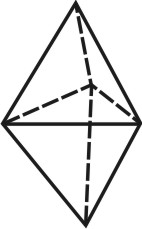
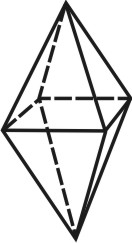
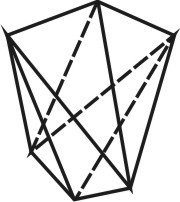
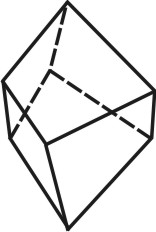
4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

а) модель		б) эпюр
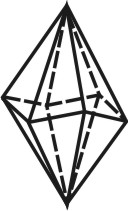
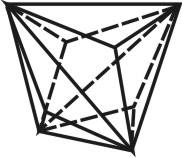
Рисунок 70. Тетраэдр

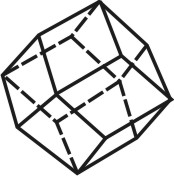
Гексаэдр — правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

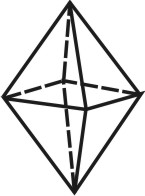
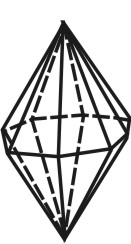
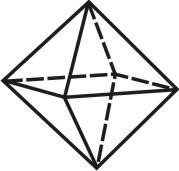
Октаэдр — правильный восьмигранник ( рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

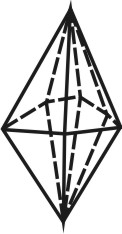
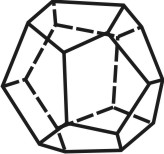
Додекаэдр — правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

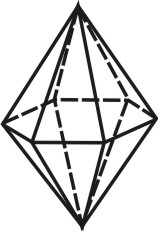
Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
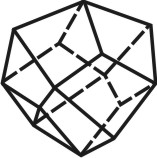
Рисунок 74. Икосаэдр

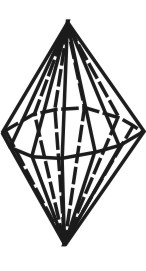
5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Источник

Кристаллография и кристаллохимия

Простые формы.

Формой многогранника называется совокупность всех его граней. Она определяется количеством всех сортов граней, взаимным расположением и соотношением размеров граней разного сорта. По внешнему виду кристаллы разделяются на две группы. К первой относятся такие кристаллы, которые состоят из одинаковых и симметрично расположенных граней (т.е. граней одного сорта). Они представляют собой простые формы. В простой форме все грани связаны между собой элементами симметрии и выводятся из одной заданной грани посредством этих элементов. Ко второй группе относятся кристаллы, обладающие различными по очертаниям и величине гранями (т.е. гранями разного сорта). Эти многогранники являются комбинациями, представляющими собой совокупность двух или нескольких простых форм. Количество простых форм, участвующих в сложении комбинационного многогранника, определяется количеством сортов граней. Всего известно 47 типов простых форм: 7 – для низшей категории, 25 – для средней и 15 – для высшей категории (таблица). Комбинаций возможно бесконечное количество.

Характеристика простых форм

Название простой формы

Число и расположение граней

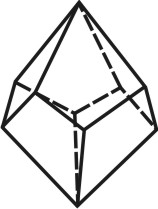
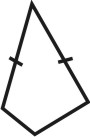
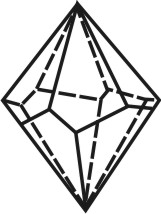
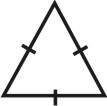
Изображение простой формы

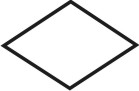
Две параллельные грани

Две пересекающиеся грани

Четыре попарно (через одну) параллельные грани

Четыре непараллельные грани, по три пересекающиеся в каждой вершине

Четыре грани, пересекающиеся в одной вершине

Восемь граней, располагающихся одна под другой, пересекающиеся в двух вершинах

Три параллельные грани, в сечении треугольник

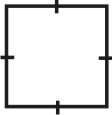
Четыре параллельные (здесь и далее относительно главной оси) грани, в сечении квадрат

Шесть параллельных граней, в сечении шестиугольник

Шесть параллельных граней, в сечении дитригон (равносторонний шестиугольник, с углами, повторяющимися через один).

Восемь параллельных граней, в сечении дитетрагон (равносторонний восьмиугольник с углами, повторяющимися через один).

Двенадцать параллельных граней, в сечении дигексагон (равносторонний двенадцатиугольник с углами, повторяющимися через один.

Три равнонаклонные грани, пересекающиеся в одной точке на главной оси L ₃.

Четыре равнонаклонные грани, пересекающиеся в одной точке на главной оси L ₄.

Шесть равнонаклоненных граней, пересекающиеся в одной точке на главной оси L ₆.

Шесть равнонаклоненных граней, пересекающихся в одной точке на главной оси L ₃; в сечении дитригон.

Восемь равнонаклоненных граней, пересекающихся в одной точке на главной оси L ₄, в сечении дитетрагон.

Двенадцать равнонаклоненных граней, пересекающихся в одной точке на главной оси L ₆; в сечении дигексагон.

Шесть равнонаклоненных граней одна под другой, пересекающихся по три в точках на главной оси L ₃ (две тригональные пирамиды, сложенные основаниями).

Восемь равнонаклоненных граней, одна под другой, пересекающиеся по четыре в двух точках на главной оси L ₄ (две тетрагональные пирамиды, сложенные основаниями).

Двенадцать равнонаклоненных граней, одна под другой, пересекающихся по шесть в двух точках на главной оси L ₆ (две гексагональные пирамиды, сложенные основаниями).

Двенадцать равнонаклоненных граней, располагающихся одна под другой, пересекающиеся в двух точках на главной оси L ₃ (две дитригональные пирамиды, сложенные основаниями).

Шестнадцать равнонаклоненных граней, одна под другой пересекающихся по восемь в двух точках на главной оси L ₄ (две тетрагональные пирамиды, сложенные основаниями).

Двадцать четыре равнонаклоненных грани, одна под другой, пересекающиеся по 12 в двух точках на главной оси L ₆ (две дигексагональные пирамиды, сложенные основаниями).

Четыре непараллельных грани по три пересекающиеся в каждой вершине. Нижняя грань располагается симметрично между двумя верхними (и наоборот).

Шесть граней в виде ромба по три пересекающиеся в каждой вершине, нижняя грань расположена симметрично между двумя верхними (и наоборот).

Двенадцать наклонных граней, пересекающих по шесть в двух точках на главной оси L ₃, нижняя пара граней расположенных симметрично между двумя парами верхних.

Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси L_{i 4}; нижняя пара граней располагается симметрично между двумя парами верхних.

Шесть наклонных граней, пересекающихся по три в двух точках на главной оси L ₃; нижние грани располагаются несимметрично относительно двух верхних.

Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси L ₄; нижние грани располагаются несимметрично относительно двух верхних.

Двенадцать наклонных граней, пересекающихся по шесть в двух точках на главной оси L ₆; нижние грани расположены несимметрично относительно двух верхних.

Четыре непараллельные грани, по три пересекающихся в каждой вершине.

Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.

Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.

Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.

Двадцать четыре грани, по шесть усложняющих каждую грань тетраэдра.

Восемь наклонных граней по четыре пересекающихся в каждой вершине.

Двадцать четыре наклонных грани по три усложняющие каждую грань октаэдра.

Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.

Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.

Сорок восемь граней по шесть усложняющих каждую грань октаэдра.

Шесть вертикальных и горизонтальных граней.

Двадцать четыре грани по четыре усложняющих каждую грань гексаэдра.

Двенадцатигранник из восьми наклонных, пересекающихся по четыре в двух точках, и четырех вертикальных граней.

Двенадцать наклонных граней, пересекающихся по три в каждой вершине.

Двадцать четыре грани по две усложняющие каждую грань пентагон-додекаэдра.

Простые формы бывают открытыми и закрытыми. Закрытая форма может одна образовывать кристаллический многогранник, так как грани закрытой формы полностью замыкают заключенное между ними пространство. К ним относятся дипирамиды, тетраэдры, трапецоэдры и др. Одна открытая простая форма, которыми являются, например, диэдры, пинакоиды, пирамиды и призмы, замкнутого многогранника образовать не может. Кристалл в этих случаях сформирован гранями нескольких простых форм, дающих комбинацию (не исключено, что в комбинации могут входить и закрытые формы).

Некоторые простые формы имеют две разновидности: правую и левую. Например, ромбические тетраэдры, все трапецоэдры, пентагон-тритетраэдры и др. Комбинационные многогранники также бывают правые и левые. Такие формы называют энантиоморфными (противоположно равными), это две зеркально равные фигуры, не совместимые друг с другом путем переносов и поворотов. Энантиоморфные формы возможны только в тех видах симметрии, в которых отсутствуют инверсионные оси, плоскости симметрии и центр инверсии.

Источник