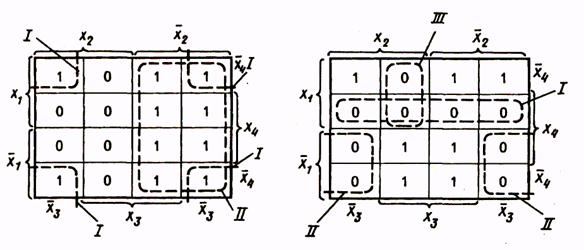
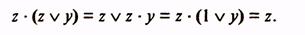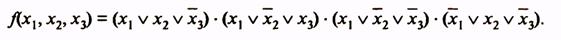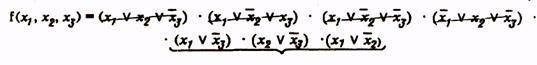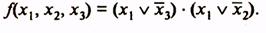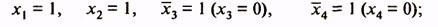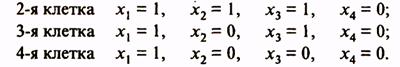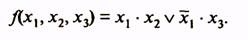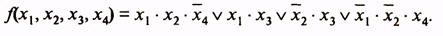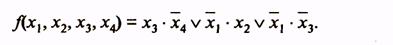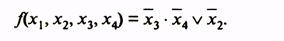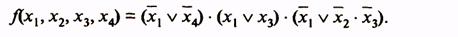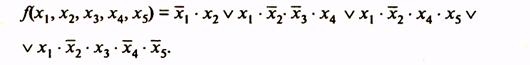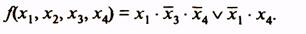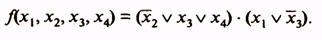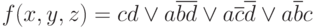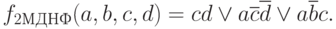какие операции лежат в основе перехода к сокращенной форме логической функции в методе квайна
Минимизация логических функций методом Квайна
Метод Квайна позволяет представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах.
Первый этап (получение сокращенной формы)
Пусть заданная функция представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.
Далее выполняется операция поглощения. Она основана на равенстве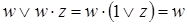 
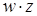
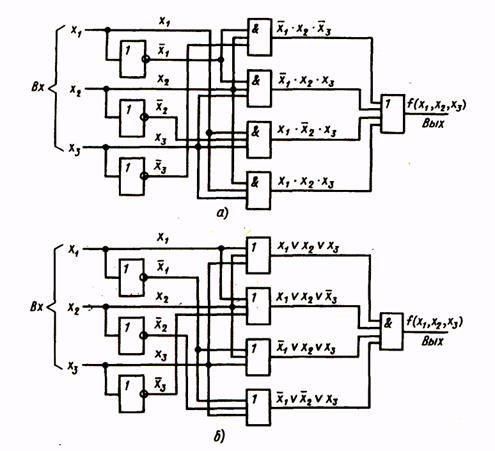
(член w поглощает член 
). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
Операции склеивания и поглощения выполняются последовательно до тех пор, пока это возможно. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции, заданной в табл. 2.
Совершенная ДНФ этой функции:
(3)
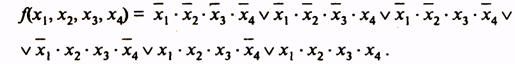
Для получения сокращенной формы проводим операции склеивания и поглощения:
(4)
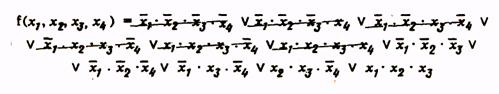
Второй этап (получение минимальной формы)
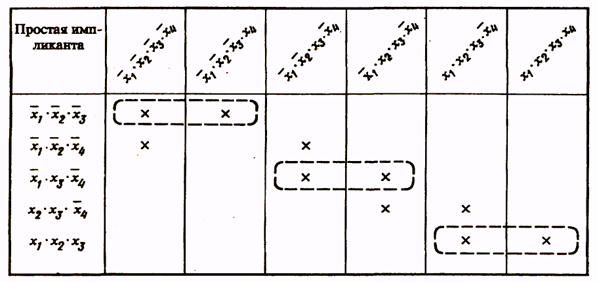
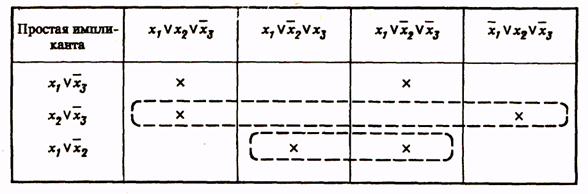
Выражение (4) представляет собой сокращенную форму логического выражения заданной функции, а члены его являются простыми импликантами функции. Переход от сокращенной формы к минимальной осуществляется с помощью импликантной матрицы, приведенной в табл. 3.
Вторая импликанта поглощает 1-й и 3-й члены СДНФ (крестики поставлены в первом и третьем столбцах второй строки) и т.д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.
В рассматриваемом примере ядро составляют импликанты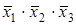 
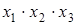
и 
(только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.
Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но, так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту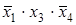 
.
Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции
(5)
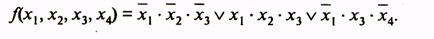
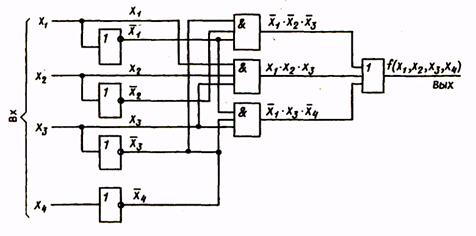
Структурная схема, соответствующая этому выражению, приведена на рис.2.
До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МКНФ) логической функции имеются следующие особенности:
— исходной для минимизации формой логического выражения заданной функции является СКНФ;
— пары склеиваемых членов имеют вид w v д: и wv x;
— операция поглощения проводится в соответствии с выражением
Рассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 4).
Совершенная КНФ рассматриваемой функции
Склеивающиеся пары членов:
1-й и 3-й члены (результат склеивания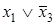 
);
1-й и 4-й члены (результат склеивания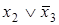 
);
2-й и 3-й члены (результат склеивания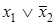 
).
Проводим операции склеивания и поглощения:
Члены операции склеивания
Полученное выражение является сокращенной формой функции.
Для перехода к минимальной форме строим импликантную матрицу (табл. 5).
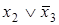
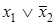
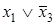
Все столбцы матрицы перекрываются импликантами и . Следовательно, член является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции
Минимизация логических функций методом карт Вейча
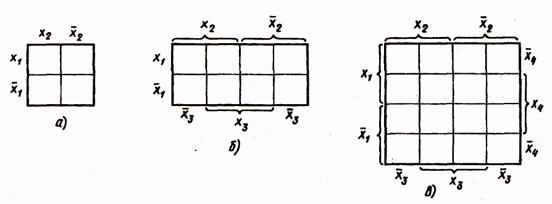
Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результатов. Он используется при минимизации относительно несложных функций (с числом аргументов до пяти). Карта Вейча представляет собой определенную форму таблицы истинности. Табл. 6 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов.
Каждая клетка карты соответствует некоторому набору значений аргументов. Этот набор аргументов определяется присвоением значения лог.1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 6в) клетки первой строки соответствуют следующим комбинациям значений аргументов:
1-я клетка 
Число клеток карты равно числу всех возможных наборов значений аргументов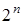 
( п — число аргументов функций ). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности (табл. 7). Таблица истинности этой функции в форме карты Вейча представлена табл. 8.
Карта Вейча определяет значения функции на всех возможных наборах значений аргументов и является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При любом переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.
Таблица 8 Таблица 9
Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).
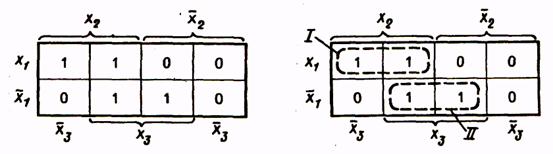
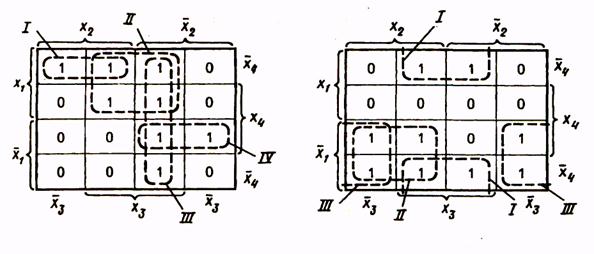
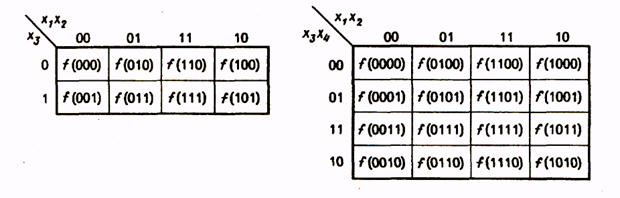
Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 9. Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 2 1 клеток, для них n-k = 3-l = 2, и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой области соответствует член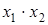 
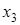
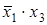
(аргумент 
здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член 
. Следовательно, МДНФ функции
Таблица 10 Таблица 11
При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением ее противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область. Иллюстрацию этого приема проведем на примере функции, представленной табл. 11. Минимальная ДНФ функции
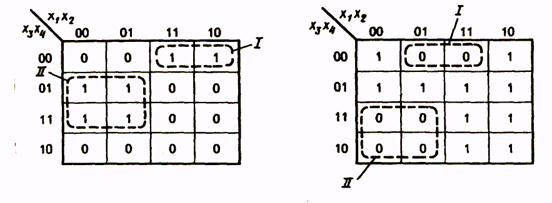
В силу допустимости такого сворачивания карты вдоль горизонтальной и вертикальной осей, например: клетки, расположенные в четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере минимизации функции, заданной табл. 12. Минимальная ДНФ функции
Таблица 12 Таблица 13
Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 13, МКНФ
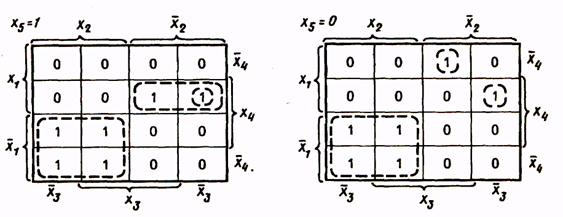
До сих пор рассматривались логические функции с числом аргументов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех. В табл. 14 показано представление с помощью карт Вейча функции пяти аргументов.
Для функции, приведенной в табл. 23, МДНФ
Для минимизации функции с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.
Минимизация функций с использованием карт Карно
Отличие карт Карно от карт Вейча заключается в способе обозначения строк и столбцов таблицы истинности. Таблица 15 иллюстрирует карты Карно для функций трех и четырех аргументов.
Таблица 16Таблица 17
Для получения МКНФ областями охватываются клетки, содержащие 0, и члены МКНФ записываются через инверсии цифр, получаемых для наборов отдельных областей. Так, для функции, представленной в табл. 17, области I соответствует набор *100 и член МКНФ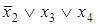 
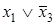
, области II — набор О*1* и член . Таким образом, МКНФ функции
1.5. Задание для выполнения
Для функции четырех аргументов F(x1,x2,x2,x4):
в) упростить функцию с помощью метода Квайна – записать МДНФ и МКНФ;
г) упростить функцию с помощью карты Вейча – записать МДНФ и МКНФ;
д) упростить функцию с помощью карты Карно – записать МДНФ и МКНФ;
е) сравнить МДНФ и МКНФ, полученные в п. в)-д);
ж) реализовать МДНФ и МКНФ на логических элементах.
Для выбора варианта взять 2 последние цифры в номере зачетной книжки.
Минимизация логических функций
Метод, основанный на теореме Квайна
Получение минимальной дизъюнктивной нормальной формы (МДНФ) выполняется в несколько этапов.
Первый этап – получение сокращенной дизъюнктивной нормальной формы (СкДНФ). Обычно он проводится на основе теоремы Квайна.
Сокращенной дизъюнктивной нормальной формой ФАЛ называется дизъюнкция всех простых импликантэтой логической функции.
Второй этап – получение минимальной дизъюнктивной (конъюнктивной) нормальной формы (МДНФ или МКНФ) с использованием импликантной (имплицентной для коньюнктивной формы) матрицы. При этом в качестве промежуточного итога получается тупиковая форма (возможно, не одна).
Теорема. Любая логическая функция, тождественно не равная нулю, представима и притом однозначно в виде сокращенной ДНФ. Любая логическая функция, тождественно не равная единице, представима, и притом однозначно, в виде сокращенной КНФ.
В данном пособии практически все теоремы будут представлены без доказательств. Их доказательства, при необходимости, можно найти в специальной литературе или в интернете.
Теорема Квайна. Если в совершенной дизъюнктивной нормальной форме логической функции провести все операции неполного склеивания и затем все операции поглощения, то в результате получается сокращенная дизъюнктивная нормальная форма этой функции.
Метод получения сокращенной дизъюнктивной нормальной формы логической функции называется методом Квайна.
Таким образом, теорема Квайна дает возможность получить из СДНФ или СКНФ их сокращенные формы (СкДНФ и СкКНФ соответственно). Эти формы будут единственными для данной логической функции.
Посмотрим, как с помощью теоремы Квайна из совершенной формы представления ФАЛ можно перейти к ее сокращенной форме.
Пример 3.1. Пусть 
Два терма, зависящие от одних и тех же переменных и отличающиеся между собой только одной переменной (в одном она имеет отрицание, а в другом – нет) называются соседними. Склеивание может проходить только между соседними термами.
Проведем все операции неполного склеивания между термами данной функции. Для этого необходимо определить возможность склеивания каждого из наборов, составляющих функцию, с любым другим набором, а именно, проверить, чтобы наборы были соседними, то есть были одного ранга (зависели от одинакового количества переменных – на первом этапе в совершенных формах это выполняется по определению) и отличались только в одной переменной. В результате получим:
После проведения всех возможных операций поглощения в данной функции получимсогласно теореме Квайнасокращенную дизъюнктивную форму исходной функции. Очевидно, что она будет единственной:
Но эта функция необязательно является минимальной формой исходной ФАЛ. Для получения минимальной дизъюнктивной нормальной формы логической функции, для которой имеются ее совершенная и сокращенная формы, следует построить импликантную (для дизъюнктивной) или имплицентную(для конюнктивной) формы матрицы, которая позволит получить вначале тупиковую форму логической функции.
Тупиковой ДНФ называется дизъюнкция простых импликант, ни одну из которых из выражения функции исключить нельзя. Некоторые функции имеют несколько тупиковых форм.
Импликантная матрица имеет следующую структуру. Ее столбцы соответствуют всем элементарным конъюнкциям исходной функции, а строки содержат все импликанты сокращенной дизъюнктивной нормальной формы (Табл. 3.2).
 |
С помощью такой таблицы можно среди импликант, входящих в состав сокращенной нормальной формы, выделить существенный импликанты, которые обязательно должны войти в состав тупиковой нормальной формы, получаемой в результате обработки данной матрицы.
Существенная импликанта характеризуется тем, что только она покрывает какой-либо из наборов совершенной формы (в соответствующем столбце матрицы содержится только одна отметка).
В рассматриваемом случае таких существенных импликант будет две: cd и 
. Они покрывают все минтермы исходной функции, кроме 
. Данный минтерм может быть покрыт как импликантой
, так и импликантой 
.
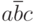
В результате мы получим две тупиковые нормальные формы:
и
Тупиковые формы, содержащие наименьшее количество символов, будут минимальными.Обе полученные выше минимальные формы содержат одинаковое число символов. Так что по принятому нами критерию их обе можно считать минимальными:
и
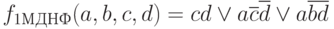
Таким образом, определенные выше дизъюнктивные нормальные формы – сокращенная, тупиковая и минимальная находятся в следующем соотношении. Тупиковая ДНФ получается из сокращенной путем удаления некоторых слагаемых. Минимальная ДНФ находится среди тупиковых. Сокращенная форма для одной логической функции – единственная. Тупиковых и минимальных форм может быть несколько.
Минимизация логических функций
Метод, основанный на теореме Квайна
Получение минимальной дизъюнктивной нормальной формы (МДНФ) выполняется в несколько этапов.
Первый этап – получение сокращенной дизъюнктивной нормальной формы (СкДНФ). Обычно он проводится на основе теоремы Квайна.
Сокращенной дизъюнктивной нормальной формой ФАЛ называется дизъюнкция всех простых импликантэтой логической функции.
Второй этап – получение минимальной дизъюнктивной (конъюнктивной) нормальной формы (МДНФ или МКНФ) с использованием импликантной (имплицентной для коньюнктивной формы) матрицы. При этом в качестве промежуточного итога получается тупиковая форма (возможно, не одна).
Теорема. Любая логическая функция, тождественно не равная нулю, представима и притом однозначно в виде сокращенной ДНФ. Любая логическая функция, тождественно не равная единице, представима, и притом однозначно, в виде сокращенной КНФ.
В данном пособии практически все теоремы будут представлены без доказательств. Их доказательства, при необходимости, можно найти в специальной литературе или в интернете.
Теорема Квайна. Если в совершенной дизъюнктивной нормальной форме логической функции провести все операции неполного склеивания и затем все операции поглощения, то в результате получается сокращенная дизъюнктивная нормальная форма этой функции.
Метод получения сокращенной дизъюнктивной нормальной формы логической функции называется методом Квайна.
Таким образом, теорема Квайна дает возможность получить из СДНФ или СКНФ их сокращенные формы (СкДНФ и СкКНФ соответственно). Эти формы будут единственными для данной логической функции.
Посмотрим, как с помощью теоремы Квайна из совершенной формы представления ФАЛ можно перейти к ее сокращенной форме.
Пример 3.1. Пусть
Два терма, зависящие от одних и тех же переменных и отличающиеся между собой только одной переменной (в одном она имеет отрицание, а в другом – нет) называются соседними. Склеивание может проходить только между соседними термами.
Проведем все операции неполного склеивания между термами данной функции. Для этого необходимо определить возможность склеивания каждого из наборов, составляющих функцию, с любым другим набором, а именно, проверить, чтобы наборы были соседними, то есть были одного ранга (зависели от одинакового количества переменных – на первом этапе в совершенных формах это выполняется по определению) и отличались только в одной переменной. В результате получим:
После проведения всех возможных операций поглощения в данной функции получимсогласно теореме Квайнасокращенную дизъюнктивную форму исходной функции. Очевидно, что она будет единственной:
Но эта функция необязательно является минимальной формой исходной ФАЛ. Для получения минимальной дизъюнктивной нормальной формы логической функции, для которой имеются ее совершенная и сокращенная формы, следует построить импликантную (для дизъюнктивной) или имплицентную(для конюнктивной) формы матрицы, которая позволит получить вначале тупиковую форму логической функции.
Тупиковой ДНФ называется дизъюнкция простых импликант, ни одну из которых из выражения функции исключить нельзя. Некоторые функции имеют несколько тупиковых форм.
Импликантная матрица имеет следующую структуру. Ее столбцы соответствуют всем элементарным конъюнкциям исходной функции, а строки содержат все импликанты сокращенной дизъюнктивной нормальной формы (Табл. 3.2).
|
С помощью такой таблицы можно среди импликант, входящих в состав сокращенной нормальной формы, выделить существенный импликанты, которые обязательно должны войти в состав тупиковой нормальной формы, получаемой в результате обработки данной матрицы.
Существенная импликанта характеризуется тем, что только она покрывает какой-либо из наборов совершенной формы (в соответствующем столбце матрицы содержится только одна отметка).
В рассматриваемом случае таких существенных импликант будет две: cd и . Они покрывают все минтермы исходной функции, кроме . Данный минтерм может быть покрыт как импликантой, так и импликантой .
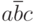
В результате мы получим две тупиковые нормальные формы:
и
Тупиковые формы, содержащие наименьшее количество символов, будут минимальными.Обе полученные выше минимальные формы содержат одинаковое число символов. Так что по принятому нами критерию их обе можно считать минимальными:
и
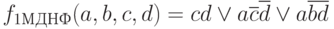
Таким образом, определенные выше дизъюнктивные нормальные формы – сокращенная, тупиковая и минимальная находятся в следующем соотношении. Тупиковая ДНФ получается из сокращенной путем удаления некоторых слагаемых. Минимальная ДНФ находится среди тупиковых. Сокращенная форма для одной логической функции – единственная. Тупиковых и минимальных форм может быть несколько.