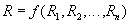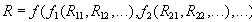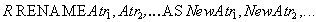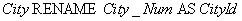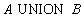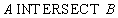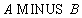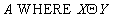какие отношения называют совместимыми по типу
Отношения, совместимые по типу



Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.
Определение
Будем называть отношения совместимыми по типу, если они имеют идентичные заголовки, а именно,
— Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении,
— Атрибуты с одинаковыми именами определены на одних и тех же доменах.
Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.
Оператор переименования атрибутов
Оператор переименования атрибутов имеет следующий синтаксис:
В результате применения оператора переименования атрибутов получаем новое отношение, с измененными именами атрибутов.
Теоретико-множественные операторы
Отношения, совместимые по типу
Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Как было показано в предыдущей лекции, отношение состоит из заголовка и тела. Операция объединения двух отношений есть объединение двух множеств кортежей, взятых из тел соответствующих отношений. Однако будет ли результат считаться отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей, нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют личные наименования. Тогда возникает вопрос, как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определены на различных доменах. Тогда опять же объединение кортежей не будет образовывать отношение.
Определение. Отношения называются совместимыми по типу, если они имеют идентичные заголовки, а именно:
1) отношения имеют одно и то же множество имен атрибутов, т. е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении;
2) атрибуты с одинаковыми именами определены на одних и тех же доменах.
Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.
Оператор переименования атрибутов имеет следующий синтаксис:
где R — отношение, A1, A2, …, An — исходные имена атрибутов, new A1, A2, …, An. — новые имена атрибутов. В результате применения оператора переименования атрибутов получаем новое отношение с измененными именами атрибутов.
Пример. Оператор rename возвращает неименованное отношение, в котором атрибут Student переименован в Head (Староста):
Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.
Определение 14.1. Будем называть отношения совместимыми по типу, если они имеют идентичные заголовки, а именно,
• Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении,
• Атрибуты с одинаковыми именами определены на одних и тех же доменах.
Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того, чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.
1.3.1 Оператор переименования атрибутов
Оператор переименования атрибутов имеет следующий синтаксис:
где 


В результате применения оператора переименования атрибутов получаем новое отношение, с измененными именами атрибутов.
Следующий оператор возвращает неименованное отношение, в котором атрибут 

1.4.1 Объединение
Определение 14.2. Объединением двух совместимых по типу отношений 





Синтаксис операции объединения:
Замечание. Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение 

Пример 14.2. Пусть даны два отношения
Таблица 14.2 Отношение B
Объединение отношений и будет иметь вид:
Таблица 14.3 Отношение A UNION B
Замечание. Как видно из приведенного примера, потенциальные ключи, которые были в отношениях 





1.4.2 Пересечение
Определение 14.3. Пересечением двух совместимых по типу отношений 





Синтаксис операции пересечения:
Пример 14.3. Для тех же отношений 

Таблица 14.4 Отношение A INTERSECT B
1.4.3 Вычитание
Определение 14.4. Вычитанием двух совместимых по типу отношений 





Синтаксис операции вычитания:
Пример 14.4. Для тех же отношений 

Таблица 14.5 Отношение A MINUS B
1.4.4 Декартово произведение
Определение 14.5. Декартовым произведением двух отношений





а тело состоит из кортежей, являющихся сцеплением кортежей отношений 


таких, что 

Замечание. Мощность произведения 




Замечание. Если в отношения 

Замечание. Перемножать можно любые два отношения, совместимость по типу при этом не требуется.
Пример 14.5. Пусть даны два отношения 

Какие отношения называют совместимыми по типу
Третья часть реляционной модели, манипуляционная часть, утверждает, что доступ к реляционным данным осуществляется при помощи реляционной алгебры или эквивалентного ему реляционного исчисления.
В реализациях конкретных реляционных СУБД сейчас не используется в чистом виде ни реляционная алгебра, ни реляционное исчисление. Фактическим стандартом доступа к реляционным данным стал язык SQL (Structured Query Language). Язык SQL представляет собой смесь операторов реляционной алгебры и выражений реляционного исчисления, использующий синтаксис, близкий к фразам английского языка и расширенный дополнительными возможностями, отсутствующими в реляционной алгебре и реляционном исчислении. Вообще, язык доступа к данным называется реляционно полным, если он по выразительной силе не уступает реляционной алгебре (или, что то же самое, реляционному исчислению), т.е. любой оператор реляционной алгебры может быть выражен средствами этого языка. Именно таким и является язык SQL.
В данной главе будут рассмотрены основы реляционной алгебры.
Замкнутость реляционной алгебры
Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов, и возвращающие отношения в качестве результата. Таким образом, реляционный оператор 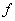
Реляционная алгебра является замкнутой, т.к. в качестве аргументов в реляционные операторы можно подставлять другие реляционные операторы, подходящие по типу:
Таким образом, в реляционных выражениях можно использовать вложенные выражения сколь угодно сложной структуры.
Каждое отношение обязано иметь уникальное имя в пределах базы данных. Имя отношения, полученного в результате выполнения реляционной операции, определяется в левой части равенства. Однако можно не требовать наличия имен от отношений, полученных в результате реляционных выражений, если эти отношения подставляются в качестве аргументов в другие реляционные выражения. Такие отношения будем называть неименованными отношениями. Неименованные отношения реально не существуют в базе данных, а только вычисляются в момент вычисления значения реляционного оператора.
Традиционно, вслед за Коддом [43], определяют восемь реляционных операторов, объединенных в две группы.
Не все они являются независимыми, т.е. некоторые из этих операторов могут быть выражены через другие реляционные операторы.
Отношения, совместимые по типу
Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.
Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.
Оператор переименования атрибутов
Оператор переименования атрибутов имеет следующий синтаксис:
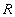
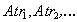
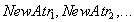
В результате применения оператора переименования атрибутов получаем новое отношение, с измененными именами атрибутов.
Следующий оператор возвращает неименованное отношение, в котором атрибут 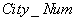
Теоретико-множественные операторы
Объединение
Определение 2. Объединением двух совместимых по типу отношений 





Синтаксис операции объединения:
Замечание. Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение 

Пример 2. Пусть даны два отношения 

| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
| 2 | Петров | 2000 |
| 3 | Сидоров | 3000 |
Таблица 1 Отношение A
| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
| 2 | Пушников | 2500 |
| 4 | Сидоров | 3000 |
Таблица 2 Отношение B
Объединение отношений 

| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
| 2 | Петров | 2000 |
| 3 | Сидоров | 3000 |
| 2 | Пушников | 2500 |
| 4 | Сидоров | 3000 |
Таблица 3 Отношение A UNION B
Замечание. Как видно из приведенного примера, потенциальные ключи, которые были в отношениях 





Пересечение
Определение 3. Пересечением двух совместимых по типу отношений 





Синтаксис операции пересечения:
Пример 3. Для тех же отношений 

| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
Таблица 4 Отношение A INTERSECT B
Вычитание
Определение 4. Вычитанием двух совместимых по типу отношений 





Синтаксис операции вычитания:
Пример 4. Для тех же отношений 

| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 2 | Петров | 2000 |
| 3 | Сидоров | 3000 |
Таблица 5 Отношение A MINUS B
Декартово произведение
Определение 5. Декартовым произведением двух отношений 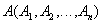
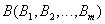


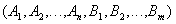
а тело состоит из кортежей, являющихся сцеплением кортежей отношений 

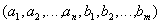
таких, что 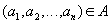
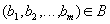
Синтаксис операции декартового произведения:
Замечание. Мощность произведения 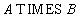




Замечание. Если в отношения 

Замечание. Перемножать можно любые два отношения, совместимость по типу при этом не требуется.
Пример 5. Пусть даны два отношения 

| Номер поставщика | Наименование поставщика |
|---|---|
| 1 | Иванов |
| 2 | Петров |
| 3 | Сидоров |
Таблица 6 Отношение A (Поставщики)
| Номер детали | Наименование детали |
|---|---|
| 1 | Болт |
| 2 | Гайка |
| 3 | Винт |
Таблица 7 Отношение B (Детали)
Декартово произведение отношений 

| Номер поставщика | Наименование поставщика | Номер детали | Наименование детали |
|---|---|---|---|
| 1 | Иванов | 1 | Болт |
| 1 | Иванов | 2 | Гайка |
| 1 | Иванов | 3 | Винт |
| 2 | Петров | 1 | Болт |
| 2 | Петров | 2 | Гайка |
| 2 | Петров | 3 | Винт |
| 3 | Сидоров | 1 | Болт |
| 3 | Сидоров | 2 | Гайка |
| 3 | Сидоров | 3 | Винт |
Таблица 8 Отношение A TIMES B
Замечание. Сама по себе операция декартового произведения не очень важна, т.к. она не дает никакой новой информации, по сравнению с исходными отношениями. Для реальных запросов эта операция почти никогда не используется. Однако операция декартового произведения важна для выполнения специальных реляционных операций, о которых речь пойдет ниже.
Специальные реляционные операторы
Выборка (ограничение, селекция)
Определение 6. Выборкой (ограничением, селекцией) на отношении 
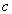

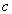
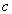

В простейшем случае условие 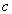
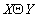
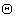
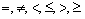
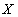
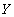

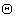
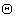
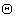
Синтаксис операции выборки:
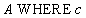
Пример 6. Пусть дано отношение 
| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
| 2 | Петров | 2000 |
| 3 | Сидоров | 3000 |
Таблица 9 Отношение A
Результат выборки 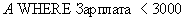
| Табельный номер | Фамилия | Зарплата |
|---|---|---|
| 1 | Иванов | 1000 |
| 2 | Петров | 2000 |
| НОМ_ВЕЩЕСТВА | ВЕЩЕСТВО |
|---|---|
| 1 | Дезоксирибонуклеиновая кислота |
| 2 | Бензин |
Таблица 25 Отношение ВЕЩЕСТВО
| НОМ_ЭЛЕМЕНТА | ЭЛЕМЕНТ |
|---|---|
| 1 | Водород |
| 2 | Гелий |
| … | … |
| 105 | … |
Таблица 26 Отношение ЭЛЕМЕНТЫ
| НОМ_ВЕЩЕСТВА | НОМ_ЭЛЕМЕНТА | ПРОЦЕНТ |
|---|---|---|
| 1 | 1 | 5 |
| 1 | 2 | 3 |
| 1 | 105 | 0.01 |
| 2 | 1 | 50 |
Таблица 27 Отношение ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ
На языке SQL такой запрос реализуется одной командой:
Невыразимость транзитивного замыкания реляционными операторами
Следующий пример иллюстрирует класс запросов, невыразимых средствами реляционной алгебры или реляционного исчисления по причине невыразимости средствами реляционной алгебры транзитивного замыкания отношений (см. гл. 1).
Пример 17. Рассмотрим отношение, описывающее сотрудников некоего предприятия. Отношение содержит данные о табельном номере сотрудника, фамилии, должности и табельном номере руководителя сотрудника – СОТРУДНИКИ ( ТАБ_НОМ, ФАМИЛИЯ, ДОЛЖНОСТЬ, ТАБ_НОМ_РУК):
| ТАБ_НОМ | ФАМИЛИЯ | ДОЛЖНОСТЬ | ТАБ_НОМ_РУК |
|---|---|---|---|
| 1 | Иванов | Директор | 1 |
| 2 | Петров | Глав.бухгалтер | 1 |
| 3 | Сидоров | Бухгалтер | 2 |
| 4 | Васильев | Начальник цеха | 1 |
| 5 | Сухов | Мастер | 4 |
| 6 | Шарипов | Рабочий | 5 |
| … | … | … | … |
Таблица 28 Отношение СОТРУДНИКИ
Рассмотрим запрос «Перечислить всех руководителей (прямых и непрямых) данного сотрудника».
Ответом на запрос может быть получен при помощи понятия транзитивного замыкания. Однако транзитивное замыкание не может быть выражено операторами реляционной алгебры.
Кросс-таблицы
Одной из задач, связанных с представлением табличных данных является построение так называемых кросс-таблиц.
Пусть имеется отношение с тремя атрибутами и потенциальным ключом, включающим первые два атрибута. Примером такого отношения могут быть данные с объемами продаж различных товаров за некоторые промежутки времени:
| Товар | Месяц | Количество |
|---|---|---|
| Компьютеры | Январь | 100 |
| Принтеры | Январь | 200 |
| Сканеры | Январь | 300 |
| Компьютеры | Февраль | 150 |
| Принтеры | Февраль | 250 |
| Сканеры | Февраль | 350 |
| … | … | … |
Таблица 29 Данные о продажах
| Товар | Январь | Февраль | … |
|---|---|---|---|
| Компьютеры | 100 | 150 | … |
| Принтеры | 200 | 250 | … |
| Сканеры | 300 | 350 | … |
Таблица 30 Кросс-таблица
Построение кросс-таблицы средствами реляционной алгебры невозможно, т.к. для этого требуется превратить данные в ячейках таблицы в наименования новых столбцов таблицы.
Выводы
Доступ к реляционным данным возможен при помощи операторов реляционной алгебры. Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов, и возвращающие отношения в качестве результата. Реляционная алгебра замкнута таким образом, что результаты одних реляционных выражений можно использовать в других выражениях.
Традиционно определяют восемь реляционных операторов, объединенных в две группы.
Теоретико-множественные операторы: объединение, пересечение, вычитание, декартово произведение.
Специальные реляционные операторы: выборка, проекция, соединение, деление.
Для выполнения некоторых реляционных операторов требуется, чтобы отношения были совместимы по типу.
Имеется несколько типов запросов, которые нельзя выразить средствами реляционной алгебры. К ним относятся запросы, требующие дать в ответе список атрибутов, удовлетворяющих определенным условиям, построение транзитивного замыкания отношений, построение кросс-таблиц. Для получения ответов на подобные запросы приходится использовать процедурные расширения реляционных языков.