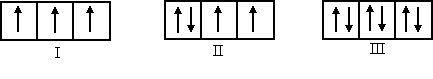какое квантовое число определяет форму атомной орбитали
Какое квантовое число определяет форму атомной орбитали
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n-1)`.
При `n=3`, `l` принимает уже три значения: `0` `(s)`; `1` `(p)` и `2` `(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещённых объёмных восьмёрок либо объёмной восьмерки с перемычкой (рис. 1).
При `n=4`, значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3` `(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения `-l` до `+l`, включая `0`.
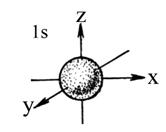
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу (`p_x`, `p_y`, `p_z`).
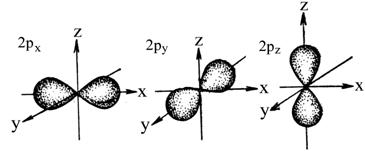
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
Спиновое квантовое число `m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n
Квантовые числа электронов.
Квантовые числа – энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
1. Главное квантовое число n характеризует общую энергию электрона и размер орбитали. Оно принимает целочисленные значения от 1: n = 1, 2, 3, 4, 5, 6, 7.
2. Орбитальное (побочное) квантовое число l характеризует форму атомной орбитали и принимает значения от 0 до n-1: 0, 1, 2, 3, …, n-1.
Электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого в s-, р-, d-, f-, g-состояниях различна.
Если l=0 (s-орбиталь), то электронное облако имеет сферическую форму и не обладает направленностью в пространстве.
Если l=1 (p-орбиталь) то электронное облако имеет форму гантели.
d- и f-орбитали имеют более сложную форму.
3. Магнитное квантовое число m характеризует количество орбиталей одинаковой формы и их ориентацию относительно внешнего электрического или магнитного поля. Квантовое число m принимает целочисленные значения в интервале –l, … –1, 0, +1, … +l. Для каждого значения разрешено 2l+1 значений числа m. Например, если l=1, то m имеет 2×1+1, т.е. 3 значения: –1, 0, +1.
4. Спиновое квантовое число s характеризует вращение электрона вокруг своей оси и принимает только 2 значения: +1/2 (↑) и –1/2 (↓).
Какое квантовое число определяет форму атомной орбитали
Главное квантовое число `n` определяет полную энергию электрона на энергетическом уровне и показывает, из скольких энергетических уровней состоит электронная оболочка атома. Принимает целочисленные положительные значения от `1` до `oo`. В периодической таблице Д. И. Менделеева `n` равно номеру периода.
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n – 1)`.
При `n=3`, `l` принимает уже три значения: `0(s)`; `1(p)` и `2(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещенных объёмных восьмёрок либо объёмной восьмёрки с перемычкой (рис. 1).
При `n=4` значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения от `-l` до `+l`, включая `0`.
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу `(p_x,p_y,p_z)`.
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
Ну и наконец, при `l=3`, то есть на `f`-подуровне, орбиталей становится семь, так как `m_l` принимает семь значений (от `−3` до `+3` через `0`). Орбитали являются более сложными объёмными структурами, и взаимное их расположение ещё более сложно.
`m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Электронная ёмкость подуровня (максимальное количество электронов на подуровне) может быть рассчитана по формуле `2(2l+1)`, а уровня — по формуле `2n^2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n
Какое квантовое число определяет форму атомной орбитали
Квантовая механика описывает движение электрона в атоме при помощи волновой функции Ψ. Общий вид этой функции находится из уравнения Шредингера, которое связывает волновую функцию Ψ с потенциальной энергией электрона Епот и его полной энергией Е:
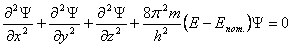
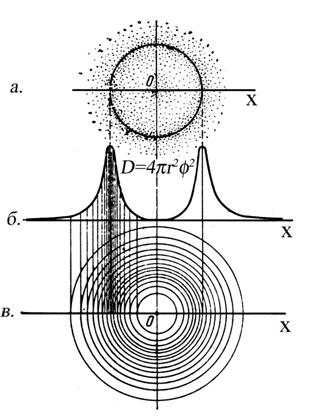
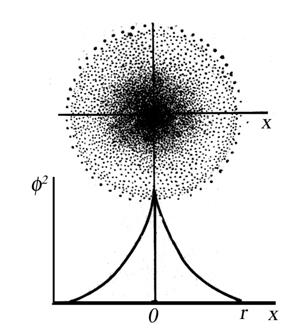
Рис. 2.1. Вероятность нахождения электрона в пространстве около ядра
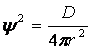
очевидно, при r = 0, т. е. в области ядра, Ψ 2 будет бесконечно большой величиной и по мере увеличения радиуса Ψ 2 уменьшается, стремясь к нулю при r → ∞ (рис. 2.2).
Рис. 2.2. Зависимость квадрата волновой функции от расстояния
Главное квантовое число n. Оно может принимать значения от 1 до бесконечности, которые определяют:
¨ номер энергетического уровня (в теории Бора – номер орбиты);
¨ интервал энергий электронов, находящихся на этом уровне;
¨ размеры орбиталей (в теории Бора – радиусы орбит);
¨ число подуровней данного энергетического уровня;
¨ в Периодической системе Д. И. Менделеева значению главного квантового числа соответствует номер периода.
Иногда пользуются буквенными обозначениями главного квантового числа, т. е. каждому численному значению n соответствует определенное буквенное обозначение:
Буквенные обозначения главного квантового числа
Численные значения n
Буквенное обозначение
Число подуровней, определяемое значением n
Магнитное квантовое число m . Вращение электрона вокруг ядра можно сравнить с движением тока по замкнутому контуру. При этом возникает магнитное поле, напряженность которого направлена перпендикулярно плоскости вращения электрона. Если атом находится во внешнем магнитном поле, то, согласно квантовомеханическим представлениям, его электроны должны расположиться так, чтобы проекции их магнитных моментов на направление этого поля были целочисленными. При этом они могут принимать как отрицательные, так и положительные значения, включая нулевое. Численное значение проекции магнитного момента и является магнитным квантовым числом. Если значение орбитального квантового числа равно ℓ, то магнитное квантовое число будет принимать значения от –ℓ до +ℓ, включая ноль. Общее количество значений будет равно 2ℓ + 1.
Число орбиталей на подуровне
Число орбиталей на подуровне
d-подуровень дает в магнитном поле пять близколежащих линий, что указывает на пять различных способов их ориентации в пространстве (рис. 2.1, в). Форма d-облаков значительно сложнее формы р-облаков. Четыре d-облака схожи по внешнему виду между собой, каждое из них как бы составлено из двух расположенных под прямым углом гантелей.
Электроны с положительным или отрицательным спинами обозначаются стрелками, направленными соответственно вверх или вниз и помещаемыми в квадрат, изображающий орбиталь. Так, символ Н1 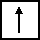
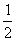
Для атома водорода, т. е. для системы «один протон и один электрон», спин электрона не влияет на энергетические или другие характеристики атома, но без представления о спине не удается объяснить возникновение молекулы Н2 из двух нейтральных атомов водорода. Благодаря введению спинового квантового числа, подсчитывается число электронов на любом уровне и подуровне и объясняются магнитные свойства атомов, ионов и молекул. У атомов, имеющих больше одного электрона в соответствии с многочисленными теоретическими предпосылками, подтвержденными экспериментальными данными, не может быть двух электронов или более с одинаковыми значениями всех четырех квантовых чисел. Это принцип (или запрет) Паули. Любые два электрона в атоме должны отличаться, по крайней мере, значением одного из квантовых чисел. Двум электронам атома «запрещено» быть во всех отношениях похожими друг на друга.
Наличие спаренных или неспаренных электронов в атомах, ионах или молекулах устанавливается экспериментально изучением магнитных свойств. Вещества c неспаренными электронами парамагнитны, т. е. эти вещества проводят магнитные силовые линии лучше, чем вакуум, и магнитное поле втягивает эти вещества. Это вызвано взаимодействием спинов электронов как элементарных магнитов с внешним магнитным полем. Парамагнитны атомы водорода.
Вещества, имеющие спаренные электроны, диамагнитны, т. е. они проводят магнитные силовые линии хуже, чем вакуум, и магнитное поле их выталкивает. Диамагнитны молекулы H 2, N 2 O 4, атомы Не, А r и др.
Увеличение числа электронов в атоме подчиняется определенным законам, что приводит к строгому расположению элементов в периодической системе и периодическому повторению их свойств. Рассмотрим некоторые основные положения электронного строения атомов.
Например, на первом энергетическом уровне могут находиться только два электрона, так как при n = ℓ ℓ может принимать только одно значение ℓ = n – 1 = 0: возможно только s-состояние. При ℓ = 0 m = 0, т. е. имеется одна s-орбиталь, на которой размещаются два электрона с разными спинами: S =+ 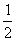
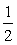
Квантовые числа
Материалы портала onx.distant.ru
Квантовые числа
Общая характеристика квантовых чисел
Принцип (запрет) Паули
Правило Хунда
Примеры решения задач
Задачи для самостоятельного решения
Общая характеристика квантовых чисел
| Значение n | 1 | 2 | 3 | 4 | 5 | 6 |
| Обозначение слоя | K | L | M | N | O | P |
Различия в энергиях электронов, принадлежащих к различным подуровням данного энергетического уровня, отражает побочное (орбитальное) квантовое число l. Электроны в атоме с одинаковыми значениями n и l составляют энергетический подуровень (электронную оболочку). Максимальное число электронов в оболочке Nl:
Побочное квантовое число принимает целые значения 0, 1, … (n – 1). Обычно l обозначается не цифрами, а буквами:
| Значение l | 0 | 1 | 2 | 3 | 4 |
| Обозначение орбитали | s | p | d | f | g |
Орбиталь – пространство вокруг ядра, в котором наиболее вероятно нахождение электрона.
Побочное (орбитальное) квантовое число l характеризует различное энергетическое состояние электронов на данном уровне, форму орбитали, орбитальный момент импульса электрона.
Таким образом, электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого зависит от значения l. Так, если l = 0, (s-орбиталь), то электронное облако имеет сферическую симметрию. При l = 1 (p-орбиталь) электронное облако имеет форму гантели. d-орбитали имеют различную форму: dz 2 — гантель, расположенная по оси Z с тором в плоскости X – Y, dx2 — y2 — две гантели, расположенные по осям X и Y; dxy, dxz, dyz, — две гантели, расположенные под 45 o к соответствующим осям.
Магнитное квантовое число ml характеризует ориентацию орбитали в пространстве, а также определяет величину проекции орбитального момента импульса на ось Z. ml принимает значения от +l до — l, включая 0. Общее число значений ml равно числу орбиталей в данной электронной оболочке.
Магнитное спиновое квантовое число ms характеризует проекцию собственного момента импульса электрона на ось Z и принимает значения +1/2 и –1/2 в единицах h/2p (h – постоянная Планка).
Принцип (запрет) Паули
В атоме не может быть двух электронов со всеми четырьмя одинаковыми квантовыми числами. Принцип Паули определяет максимальное число электронов Nn, на электронном слое с номером n:
На первом электронном слое может находиться не более двух электронов, на втором – 8, на третьем – 18 и т. д.
Правило Хунда
Заполнение энергетических уровней происходит таким образом, чтобы суммарный спин был максимальным. Например, три р-электрона на орбиталях р-оболочки располагаются следующим образом:
Таким образом, каждый электрон занимает одну р-орбиталь.
Примеры решения задач
Задача 1. Охарактеризуйте квантовыми числами электроны атома углерода в невозбужденном состоянии. Ответ представьте в виде таблицы.
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
| 6 | 2 | 1 | 0 | +1/2 |
Задача 2. Охарактеризуйте квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представьте в виде таблицы.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 | 0 | 0 | –1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | –1 | +1/2 |
| 6 | 2 | 1 | 1 | –1/2 |
Решение. Согласно правилу Хунда электроны в квантовых ячейках располагаются следующим образом:
Значения главного, побочного и спинового квантовых чисел у электронов одинаковы и равны n=4, l=2, ms=+1/2. Рассматриваемые электроны отличаются значениями квантовых чисел ml.
| № электрона | n | l | ml | ms |
| 1 | 4 | 2 | 2 | +1/2 |
| 2 | 4 | 2 | 1 | +1/2 |
| 3 | 4 | 2 | 0 | +1/2 |
| 4 | 4 | 2 | –1 | +1/2 |
| 5 | 4 | 2 | –2 | +1/2 |
Задача 4. Рассчитайте максимальное число электронов в электронном слое с n = 4.
Решение. Максимальное число электронов, обладающих данным значением главного квантового числа, рассчитываем по формуле (2). Следовательно, в третьем энергетическом уровне может быть не более 32 электронов.
Задача 5. Рассчитайте максимальное число электронов в электронной оболочке с l = 3.
Решение:
Максимальное число электронов в оболочке определяется выражением (1). Таким образом, максимальное число электронов в электронной оболочке с l = 3 равно 14.
Задачи для самостоятельного решения
1. Охарактеризуйте квантовыми числами электроны атома бора в основном состоянии. Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
2. Охарактеризуйте квантовыми числами d-электроны атома железа в основном состоянии. Ответ представьте в виде таблиц:
Расположение 3d-электронов атома железа на орбиталях:
Значения квантовых чисел этих электронов:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
Шесть 3d-электронов атома железа располагаются на орбиталях следующим образом
Квантовые числа этих электронов приведены в таблице
| № электрона | n | l | ml | ms |
| 1 | 3 | 2 | 2 | +1/2 |
| 2 | 3 | 2 | 1 | +1/2 |
| 3 | 3 | 2 | 0 | +1/2 |
| 4 | 3 | 2 | — 1 | +1/2 |
| 5 | 3 | 2 | — 2 | +1/2 |
| 6 | 3 | 2 | 2 | — 1/2 |
3. Каковы возможные значения магнитного квантового числа ml, если орбитальное квантовое число l = 3?
Ответ: ml = +3; +2; +1; 0, — 1, — 2, — 3.
4. Охарактеризуйте квантовыми числами находящиеся во втором электронном слое электроны:
Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
| 7 | ? | ? | ? | ? |