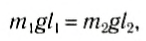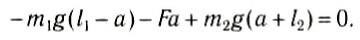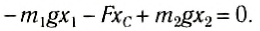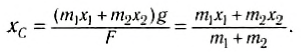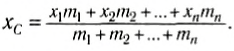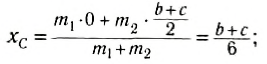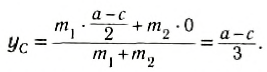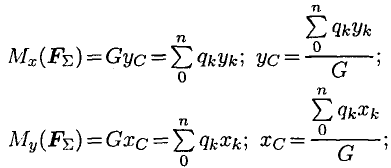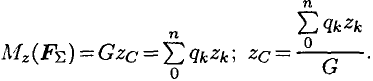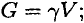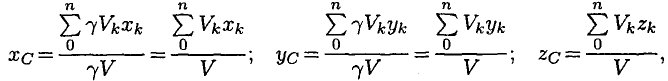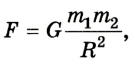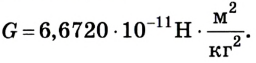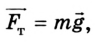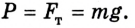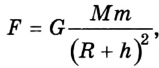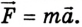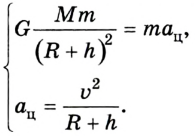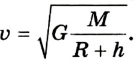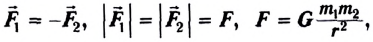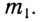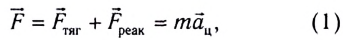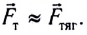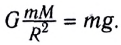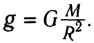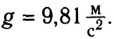какова точка приложения силы тяжести

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

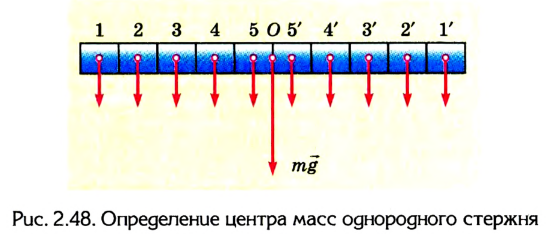
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

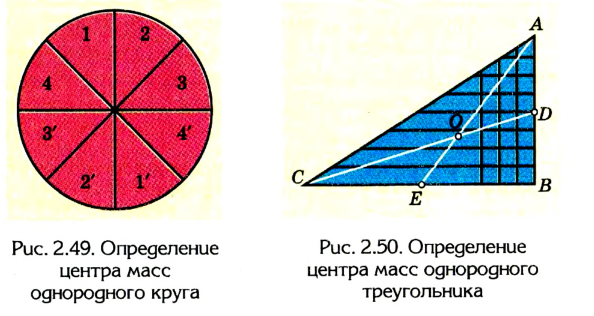
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

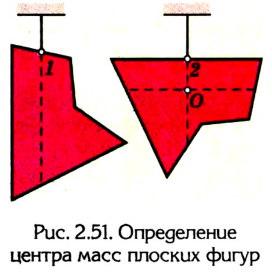
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

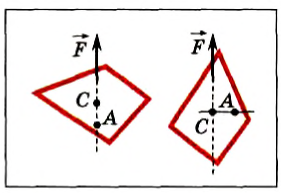
Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

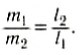
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

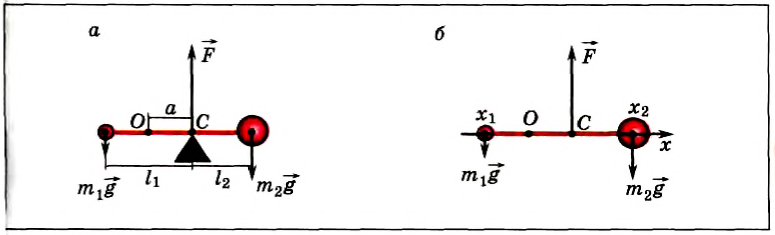
Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂. m_n, и если известны координаты центров масс этих элементов x₁, x₂. x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Сила тяжести

Сила тяжести

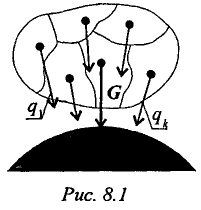
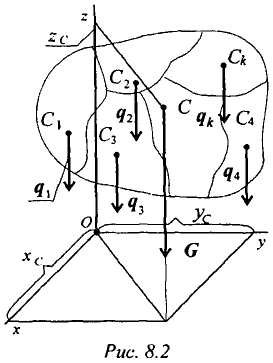
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.

Точка приложения силы тяжести

Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.

Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).

Тело состоит из частей, силы тяжести которых qk приложены в центрах тяжести (ЦТ) этих частей.

Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре .

и — координаты центра тяжести .

и — координаты центров тяжести частей тела.

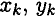
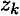
Из теоремы Вариньона следует:

аналогично для оси :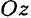

В однородном теле сила тяжести пропорциональна объему :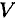

где 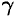— вес единицы объема.

Следовательно, в формулах для однородных тел:

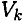
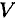
где — объем элемента тела; — объем всего тела.

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

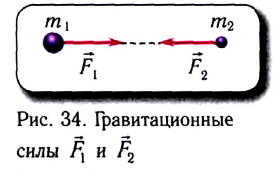
Гравитационные силы:

В механике изучают силы тяготения или гравитационные силы, силы упругости и силы трения.

Гравитационная сила является проявлением закона всемирного тяготения, который сформулировал Ньютон: гравитационное притяжение существует между всеми телами; любые два тела, размерами которых можно пренебречь, притягиваются друг к другу с силой, которая прямо пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними (рис. 2.10):

Ее числовое значение впервые определил путем эксперимента английский ученый Г. Кавендиш в 1798 г.

Закон всемирного тяготения справедлив для точечных тел, размеры которых намного меньше расстояния между ними, а также для больших однородных шаров, например, системы Земля-Луна, или однородного шара и точечного тела (движение искусственного спутника вокруг Земли). Гравитационная сила в данном случае направлена вдоль линии, которая соединяет центры масс взаимодействующих тел.

Гравитационная сила, с которой Земля притягивает к себе тела, придавая им ускорение свободного падения, называется силой тяжести (рис. 2.11):

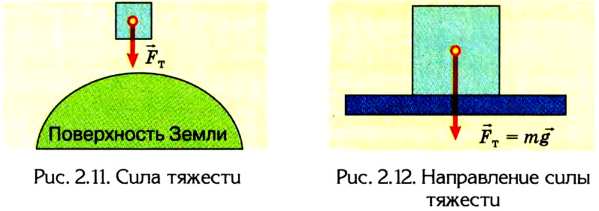
Сила тяжести всегда приложена к центру масс тела и направлена вертикально вниз, перпендикулярно к горизонтальной поверхности (рис. 2.12).

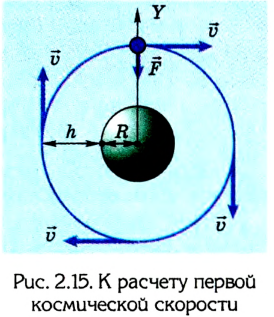
При решении задач по физике достаточно часто используют понятие веса тела, т. е. силы, с которой тело действует на подставку или подвес вследствие притяжения Земли (рис. 2.13).

Если тело в инерциальной системе отсчета неподвижно или движется равномерно и прямолинейно, то его вес равен силе тяжести:

Масса характеризует инертные и гравитационные свойства тел.

Рассмотрим пример решения задачи на действие гравитационной силы.

Пример решения задачи:

Какую скорость нужно сообщить телу, чтобы оно стало искусственным спутником планеты массой М, радиус которой R, и вращалось по орбите на высоте h?

Сделаем рисунок в соответствии с условием задачи (рис. 2.15).

Будем считать, что планета имеет форму шара, а спутник не испытывает действия сил сопротивления.

Таким образом, на спутник действует лишь сила гравитационного притяжения к планете:

Как правило, во время движения по окружности выбирают ось координат ОУ так, чтобы она была направлена к центру окружности или, наоборот, от него.

Для искусственного спутника планеты запишем уравнение второго закона механики Ньютона в векторной форме:

Поскольку скорость спутника постоянна (по значению), то сила притяжения к планете придает ему лишь центростремительное ускорение 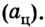Итак, мы имеем систему уравнений:

Данная система уравнений легко решается методом подстановки:

Искомая скорость будет одинаковой для спутников различной массы, поскольку не зависит от нее. Например, для любой планеты она будет зависеть лишь от высоты спутника над ее поверхностью.

Чтобы найти значение скорости тела, которая необходима искусственному спутнику планеты, т. е. первой космической скорости, воспользуемся параметрами Земли: 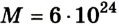кг, R- 6400 км, h = 300 км. Подставив их в формулу, получим v= 7,7 км/с.

Ответ: v = 7,7 км/с (для Земли).

Гравитационные силы. Закон всемирного тяготения. Сила тяжести. Ускорение свободного падения

Сила тяжести, действующая на тело, прямо пропорциональна его массе: 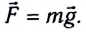Направление силы тяжести принимают за направление вертикали в данной точке земной поверхности.

В большинстве механических процессов силы возникают при непосредственном (механическом) контакте взаимодействующих тел. Это справедливо, например, в случае сил упругости, трения, реакции опоры.

Однако сила гравитационного взаимодействия способна действовать на расстоянии, т. е. она существует даже тогда, когда тела не находятся в контакте.
Гравитационные силы (силы тяготения) — это силы, с которыми притягиваются друг к другу все тела во Вселенной.

Модуль и направление гравитационных сил определяется законом всемирного тяготения:

где 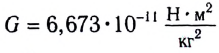— гравитационная постоянная.

Заметим, что гравитационная постоянная численно равна силе, с которой взаимодействуют две материальные точки массами 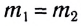= 1,000 кг, находящиеся на расстоянии r= 1,000 м друг от друга.

Впервые гравитационную постоянную G измерил в 1798 году Г. Кавендиш с помощью крутильных весов.

Закон всемирного тяготения справедлив не только для двух материальных точек, но и для тел произвольной формы, размеры которых во много раз меньше расстояний между центрами тяжести тел, а также для тел шарообразной формы, где под расстоянием r понимается расстояние между центрами шаров.

Гравитационные силы обусловлены взаимным притяжением тел, рассматриваемых как материальные точки. Они направлены вдоль линии, соединяющей взаимодействующие материальные точки, и поэтому называются центральными силами.

В основе вывода закона всемирного тяготения лежат законы Кеплера, второй закон Ньютона и предположение об универсальности взаимодействия между телами независимо от их природы.

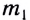
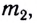
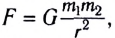
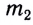
Гравитационное взаимодействие может быть описано с помощью гравитационного поля (поля сил тяготения). Тело массой может рассматриваться как источник гравитационного поля, которое притягивает тело массой находящееся на расстоянии r от него, с силой, модуль которой равен и направленной по прямой, соединяющей центры масс этих тел. Аналогично можно рассматривать тело массой как источник гравитационного поля, в котором находится тело массой

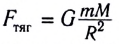
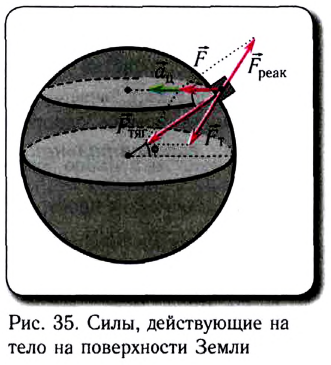
На тело, находящееся в гравитационном поле Земли, действует сила всемирного тяготения (m — масса тела, М — масса Земли, R — радиус Земли), направленная к центру Земли (рис. 35). В этом случае Землю считаем однородным шаром радиусом R.

Согласно второму закону Ньютона при вращательном движении вместе с Землей на тело со стороны Земли действует результирующая сила

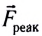
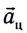
где — сила суммарной реакции земной поверхности, — центростремительное (нормальное) ускорение.

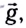
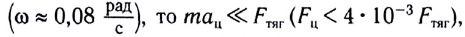
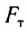
Составляющая силы всемирного тяготения, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения называется силой тяжести. Так как угловая скорость вращения Земли мала поэтому сила тяжести незначительно отличается от силы гравитационного притяжения Земли и по модулю, и по направлению, т.е.

Точку приложения силы тяжести называют центром тяжести тела. Положение центра тяжести тела в однородном гравитационном поле совпадает с его центром масс.

По второму закону Ньютона

Откуда ускорение свободного падения

Следовательно, ускорение свободного падения g не зависит от массы m тела, а определяется массой Земли М и ее радиусом R.

Ускорение свободного падения зависит от:

широты 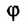данной точки (Земля — неинерциальная система отсчета) земной

При подъеме тела сила тяжести убывает с высотой сравнительно медленно. Так, на высоте 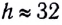км над поверхностью Земли она уменьшается всего на 1 %.

Нормальным ускорением свободного падения называется ускорение свободного падения на широте 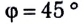на уровне моря (h = 0), измеренное при нормальных условиях. Численно оно равно

Гравитационное поле, в котором на материальную точку массой m в любой точке пространства действует одинаковая сила 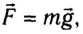называется однородным.

В рамках модели однородного гравитационного поля поверхность Земли считается горизонтальной, а сила тяжести направлена вертикально вниз.

В малых областях пространства вблизи поверхности Земли и других небесных тел такая модель применима для описания гравитационного поля. Однородное гравитационное поле называется полем тяжести.

Таким образом, ускорение свободного падения g — это ускорение, с которым движется материальная точка вблизи поверхности Земли под действием силы тяжести, в системе отсчета, связанной с Землей как телом отсчета.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник