какую форму имеет параллель эллипсоида

Эллипсоиды

Определение эллипсоида

Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

Плоские сечения эллипсоида

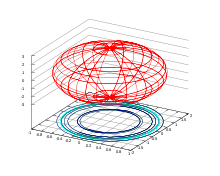
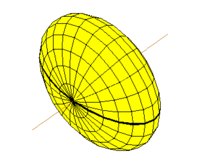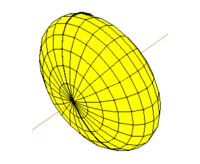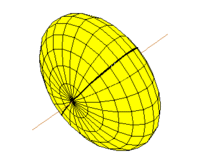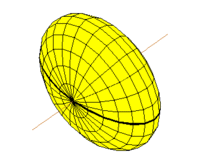
Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).

Эллипсоиды вращения

Эллипсоид, у которого полуоси попарно различны b>c)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAGAAAAAWBAMAAADNzYTXAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAXynYREhwNFB6DGRUQyCkmkAAAGUSURBVDjLY2AgHbBcIFYlkwOYcsYm51yCTRQsyLYUm9T2t9hEoxKABLsCNimep9hEmQ2AxL4AhG8c4EyJRjDlIoCige0ZkDiBJOahCmPFHYAY0RSArIFxEZCoAWJO49sJYAG4jnvKRWBaBK6D29ySgcEYqOYRkGO1tQ7iE0YPM4j0ubYoiIhIcwJEROuilgADEDE+AVr8ksEPFhnTwToYuwLYF0IEJIvBOljeMr5iYNQTYGB9CQytBoZzCTBnTrcGkqxvGNgfMsB0bACSeY0M2xgY/CAa/BQYuuAem1wNJHjfMsgtgApwmoM06IFd6Adx0rkJrI9h6qdbghPBM4Z5BlD1xRNAlB2YBDoJ5Gm9AN4nyRAHXYd4WughzJGyEC+AlLIxMGpBgvVeQsRLFUhEQAOJ+yn3E0hEwAJp3gVGjQAGcyBLQ4CBp8dycQFqxJ2wuIAacSxrjitAIi4PKBTKIAl2OVw9A+tGMKWEiGhpoAjbayBDWIH4rMMDcgfnUuI1gJM39gyEFTCaQDIe0VkUKfkTDwAVFViuYeRgnwAAAABJRU5ErkJggg==» style=»vertical-align: middle;»/>, называется трехосным (или общим).

2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.

3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.

В самом деле, если точка принадлежит эллипсоиду, то точки с координатами при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).

Источник

СОДЕРЖАНИЕ

Стандартное уравнение

Используя декартову систему координат, в которой начало координат является центром эллипсоида, а оси координат являются осями эллипсоида, неявное уравнение эллипсоида имеет стандартную форму

Параметризация

Эллипсоид можно параметризовать несколькими способами, которые проще выразить, если оси эллипсоида совпадают с осями координат. Обычный выбор

Измерение от центра, а не от полюса,

Измерение углов непосредственно к поверхности эллипсоида, а не к описанной сфере,

Объем

Это уравнение сводится к уравнению объема сферы, когда все три эллиптических радиуса равны, и к уравнению сплющенного или вытянутого сфероида, когда два из них равны.

Площадь поверхности

Площадь поверхности общего (трехосного) эллипсоида равна

Площадь поверхности эллипсоида вращения (или сфероида) может быть выражена через элементарные функции :

Примерная формула

Здесь p ≈ 1,6075 дает относительную ошибку не более 1,061%; значение p = 8 / 5 = 1,6 оптимально для эллипсоидов, близких к сферической, с относительной погрешностью не более 1,178%.

Плоские секции

Характеристики

Пересечение плоскости и сферы представляет собой окружность (либо сводится к одной точке, либо пусто). Любой эллипсоид является изображением единичной сферы при некотором аффинном преобразовании, а любая плоскость является изображением некоторой другой плоскости при таком же преобразовании. Итак, поскольку аффинные преобразования преобразуют круги в эллипсы, пересечение плоскости с эллипсоидом является эллипсом, единственной точкой или пусто. Очевидно, что сфероиды содержат круги. Это также верно, но менее очевидно, для трехосных эллипсоидов (см. Круглый раздел ).

Определение эллипса плоского сечения

его единичный вектор нормали. Следовательно

является центром пересечений окружности и

его радиус (см. диаграмму).

Если m _w = ± 1 (т. Е. Плоскость горизонтальна), пусть

Штифтовая конструкция

Построение «кегли и струны» эллипсоида вращения дается конструкцией вращающегося эллипса «кегли».

Построение точек трехосного эллипсоида сложнее. Первые идеи принадлежат шотландскому физику Дж. К. Максвеллу (1868 г.). Основные исследования и распространение на квадрики были выполнены немецким математиком О. Штауде в 1882, 1886 и 1898 годах. Описание конструкции эллипсоидов и гиперболоидов с помощью булавок и струн содержится в книге « Геометрия и воображение», написанной Д. Гильберт и С. Фоссен тоже.

Этапы строительства

с вершинами и фокусами эллипса

Полуоси

Уравнения для полуосей сгенерированного эллипсоида могут быть получены путем специального выбора для точки P :

Converse

Конфокальные эллипсоиды

Если Е представляет собой эллипсоид конфокальный к Е с квадратами его полуосей

Верно и обратное утверждение: если выбрать вторую строку длины l и определить

действительны, что означает, что два эллипсоида конфокальны.

Предельный случай, эллипсоид вращения

Свойства фокальной гиперболы

Свойство фокального эллипса

В общем положении

Как квадрика

Параметрическое представление

Ключом к параметрическому представлению эллипсоида в общем положении является альтернативное определение:

Аффинное преобразование может быть представлено в виде перевода с вектором ф ₀ и регулярным 3 × 3 матрицы A :

Параметрическое представление эллипсоида общего положения может быть получено параметрическим представлением единичной сферы (см. Выше) и аффинным преобразованием:

Приложения

Эллипсоидальная форма находит множество практических применений:

Динамические свойства

Масса эллипсоида равномерной плотности р является

В моменты инерции эллипсоида однородной плотности являются

При a = b = c эти моменты инерции сводятся к моментам инерции для сферы однородной плотности.

Эллипсоиды и кубоиды стабильно вращаются вдоль своей большой или малой оси, но не вдоль средней оси. Это можно увидеть экспериментально, бросив ластик с некоторым вращением. Кроме того, соображения момента инерции означают, что вращение вдоль большой оси более легко нарушить, чем вращение вдоль малой оси.

Одним из практических последствий этого является то, что разносторонние астрономические тела, такие как Хаумеа, обычно вращаются вдоль своих малых осей (как и Земля, которая просто сплюснута ); кроме того, из-за приливной блокировки спутники находятся на синхронной орбите, такие как орбита Мимаса, с их большой осью, выровненной радиально по отношению к их планете.

Вращающееся тело из однородной самогравитирующей жидкости примет форму сфероида Маклорена (сплюснутый сфероид) или эллипсоида Якоби (разносторонний эллипсоид), когда оно находится в гидростатическом равновесии и при умеренных скоростях вращения. При более быстром вращении можно ожидать неэллипсоидальной грушевидной или яйцевидной формы, но они нестабильны.

Динамика жидкостей

По вероятности и статистике

Таким образом, функция плотности представляет собой скалярное преобразование квадратичного выражения в скалярное преобразование. Более того, уравнение для любой поверхности изоплотности утверждает, что выражение квадрики равно некоторой константе, специфичной для этого значения плотности, а поверхность изоплотности является эллипсоидом.

В высших измерениях

Источник

Эллипсоид

Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:

где — произвольные положительные числа.

Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.

В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.

Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.

Площадь поверхности эллипсоида вращения:

Литература

Полезное

Смотреть что такое «Эллипсоид» в других словарях:

Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь

ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка

эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка

Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия

эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов

ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь

Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии

эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации

ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь

Источник

Эллипсоид: характеристики и примеры

Содержание:

Топор 2 + Автор 2 + Cz 2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0

Помимо эллипсоида, есть еще пять квадрик: одностворчатый и двухлистный гиперболоид, два типа параболоида (гиперболический и эллиптический) и эллиптический конус. Его следы также имеют коническую форму.

Эллипсоид также можно выразить стандартным уравнением в декартовых координатах. Эллипсоид с центром в начале координат (0,0,0), выраженный таким образом, напоминает эллипс, но с дополнительным членом:

Ценности к, б Y c являются действительными числами больше 0 и представляют три полуоси эллипсоида.

Характеристики эллипсоида

— Стандартное уравнение

Стандартное уравнение в декартовых координатах для эллипса с центром в точке (ч, к, м) это:

— Параметрические уравнения эллипсоида

В сферических координатах эллипсоид можно описать следующим образом:

Полуоси эллипсоида остаются a, b и c, а параметрами являются углы θ и φ на следующем рисунке:

— Следы эллипсоида

В случае эллипсоида такие кривые представляют собой эллипсы, а иногда и окружности.

— Объем

Объем V эллипсоида равен (4/3) π умноженным на произведение трех его полуосей:

Частные случаи эллипсоида

-Эллипсоид становится сферой, когда все полуоси имеют одинаковый размер: a = b = c ≠ 0. Это имеет смысл, поскольку эллипсоид подобен сфере, которая была растянута по-разному вдоль каждой оси. ось.

-Сфероид представляет собой эллипсоид, в котором две полуоси идентичны, а третья другая, например, это может быть a = b ≠ c.

Сфероид также называют эллипсоидом вращения, потому что он может быть образован вращением эллипсов вокруг оси.

Если ось вращения совпадает с большой осью, сфероид имеет вид вытянутый, но если он совпадает с малой осью, он сплюснутый:

Мера уплощения сфероида (эллиптичность) определяется разницей в длине между двумя полуосями, выраженной в дробной форме, то есть это единица сплющивания, определяемая как:

Справочный эллипсоид

Планеты и звезды в целом обычно не являются идеальными сферами, потому что вращательное движение вокруг их осей сглаживает тело на полюсах и выпячивает его на экваторе.

Вот почему Земля похожа на сплюснутый сфероид, хотя и не такой преувеличенный, как на предыдущем рисунке, а газовый гигант Сатурн со своей стороны является самой плоской из планет Солнечной системы.

Тщательные измерения, сделанные на земном шаре, позволили построитьопорный эллипсоид Земли как наиболее точный способ математической работы.

Звезды также имеют вращательные движения, которые придают им более или менее уплощенные формы. Быстрая звезда Ахернар, восьмая по яркости звезда на ночном небе, в южном созвездии Эридана, имеет удивительно эллиптическую форму по сравнению с большинством из них. Это 144 световых года от нас.

С другой стороны, несколько лет назад ученые обнаружили самый сферический объект из когда-либо обнаруженных: звезду Кеплер 11145123, находящуюся на расстоянии 5000 световых лет, в два раза больше нашего Солнца и с разницей между полуосями всего в 3 км. Как и ожидалось, он тоже медленнее вращается.

Что касается Земли, то она не является идеальным сфероидом из-за неровной поверхности и местных изменений силы тяжести. По этой причине доступно более одного эталонного сфероида, и на каждом сайте выбирается наиболее подходящий для местной географии.

Помощь спутников неоценима в создании все более точных моделей формы Земли, благодаря которым известно, например, что южный полюс ближе к экватору, чем северный полюс.

Числовой пример

Найдите уравнение экваториального следа этого эллипсоида и меру его уплощения. Также сравните с эллиптичностью Сатурна, с данными, приведенными ниже:

Экваториальный радиус Сатурна: 60 ​​268 км

-Полярный радиус Сатурна: 54,364 км

Решение

Требуется система координат, центр которой мы будем считать центрированной в начале координат (центре Земли). Предположим, что вертикальная ось z и след, соответствующий экватору, лежит в плоскости xy, эквивалентной плоскости z = 0.

В экваториальной плоскости полуоси a и b равны, поэтому a = b = 3963 мили, а c = 3942 мили. Это особый случай: сфероид с центром в точке (0,0,0), как упоминалось выше.

Экваториальный след представляет собой круг радиусом R = 3963 мили с центром в начале координат. Он рассчитывается путем принятия z = 0 в стандартном уравнении:

А стандартное уравнение земного эллипсоида:

F _Сатурн = (60268-54363) км / 60268 км = 0,0980

Ссылки

Психология, криминология и их связь в человеческих ресурсах

Источник

«Шар наш земной — да что же он такое?»

В предыдущих статьях этого цикла я подробно останавливался на том, какой необходимой информацией нужно обладать, чтобы грамотно обрабатывать архивные карты, в том числе для целей навигации на местности, а также для того, чтобы стало возможным соотнести информацию, изображённую на архивной карте с современным состоянием местности.

В последней статье я подробно разобрал тему желательности (и даже, порой, необходимости) знания проекции карты. Однако геодезическая основа упоминалась вскользь, как правило только для понимания основной мысли материала, хотя именно геодезия — краеугольный камень картографии. Теперь пришло время подробно поговорить и об этом. Давайте разберём, насколько важным для операций со старыми картами является это понимание и знание и в каких случаях этими сведениями можно пренебречь.

ПРО ЭЛЛИПСОИДЫ, ГЕОИДЫ И ПРОЧИЕ «ВЫСШИЕ СФЕРЫ» ГЕОДЕЗИИ

Основную задачу, стоящую перед картографом при построении географической карты, можно сформулировать так: отобразить с наименьшими искажениями на плоском листе бумаги подлинную картину местности, которая на самом деле располагается на земной поверхности. Я здесь сознательно хочу подчеркнуть самый сложный вариант задачи, отображение именно на плоский лист. Именно в таком виде географические карты начали своё существование; лишь сравнительно недавно, уже в компьютерную эру, появились возможности изображения местности сразу на трёхмерных поверхностях (хотя и остаётся задача изображения этих трёхмерных поверхностей на плоском экране монитора, но она решается уже несколько иными способами).

Задача отображения на плоский лист земной поверхности и решается с помощью разнообразных способов, именуемых «проекциями», о которых я подробно рассказывал в предыдущей статье. Однако, все эти способы разработаны (в том числе и в математическом, формульном виде) в одном предположении: поверхность Земли имеет форму сферы или эллипсоида. Только при таких условиях становится возможным численное, математическое решение задачи.

Тем не менее, сегодня мы знаем, что наша планета имеет гораздо более сложную форму: она не является даже эллипсоидом с разными размерами своих полуосей (трёхосным эллипсоидом), и уж тем более не является простой сферой. Как же быть в этом случае?

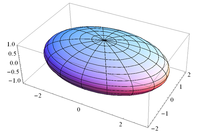
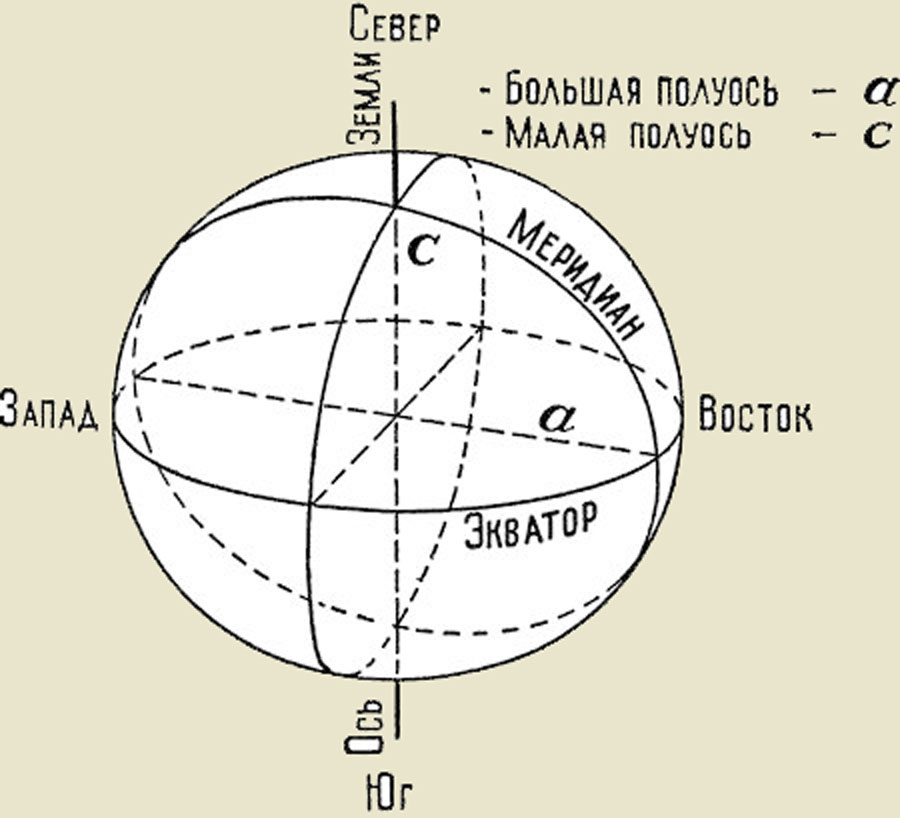
Земля как двухосный эллипсоид

Выше изображён простой двухосный эллипсоид, который также ещё называют эллипсоидом вращения. Именно эта модель и используется в картографии вплоть до нынешнего времени. Дело в том, что именно для неё возможны достаточно простые математические представления отображения её участков поверхности на ту или иную плоскость (именно об этом процессе и говорят, когда подразумевают ту или иную «проекцию»).

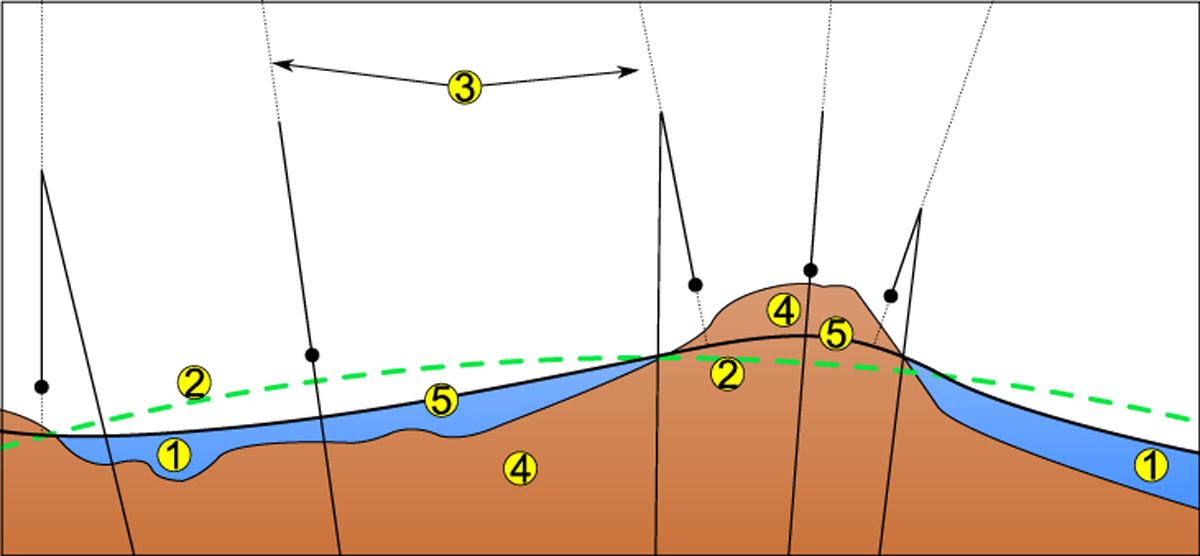
Как оно обычно бывает в жизни, реальная ситуация намного сложнее. На рисунке ниже изображён фрагмент поверхности так называемого «геоида», который (между прочим, тоже в приближении!) и описывает реальную земную поверхность.

По своему определению, поверхность геоида — это поверхность, перпендикулярная к направлению силы тяжести (отвесной линии) в каждой своей точке. Из рисунка видно, что в основном эта поверхность совпадает с поверхностью мирового океана, однако с поверхностью суши она уже совпадает лишь в некотором приближении. Ещё в большем приближении она совпадает с поверхностью эллипсоида, которая на рисунке изображена зелёной пунктирной линией.

Теперь из рисунка уже становится понятным, что наша задача усложнилась: нам нужно не только найти наилучший способ отображения эллипсоида на плоскость, но и найти наилучший способ отображения земной поверхности на эллипсоид. Стоит, однако, заметить, что само понятие «наилучший», точно так же, как и в случае с проекциями, зависит от тех целей, которые мы перед собой ставим. В частности, такая задача, как мы увидим ниже, может быть решена разными способами, в зависимости от того, ведём ли мы речь о всей земной поверхности, или лишь о её части. И здесь тоже возможны варианты, в зависимости от величины этой части.

Для того, чтобы понимать, как развивалась научная мысль в этом направлении, стоит вернуться на много веков назад.

По крайней мере, Аристотель был полностью убеждён в шарообразности Земли. Однако, первая попытка измерения её размеров принадлежит Эратосфену Киренскому (ок. 276–194 до н. э.). Я здесь не буду подробно останавливаться на изящном и остроумном способе его решения задачи; любопытный читатель легко найдёт его в сети Интернет. Упомяну лишь, что сам способ является по сути дела астрономическим, связанным с определением высоты Солнца в разных географических точках. Такие же или другие астрономические способы являются базовыми для всех измерений такого рода. К сожалению, мы не знаем, насколько точно Эратосфен измерил диаметр: дело в том, что все вычисления он проводил в типичных единицах своего времени, «стадиях», а как соотносятся «стадии» Эратосфена с современными единицами расстояний неизвестно. Встречающиеся иногда попытки оценки точности его измерений часто по принципу порочного круга выводят на определение длины стадии через его же измерения диаметра Земли. Так что давайте здесь ограничимся лишь тем бесспорным утверждением, что окружность Земли у него получилась равной 250 000 стадий, а стадия, определённая таким способом равна примерно 160 современным метрам. К этой неоднозначности «стадии Эратосфена» мы ещё будем возвращаться не раз ниже в статье.

В качестве других примеров попыток определения диаметра Земли стоит, пожалуй, упомянуть здесь индийского астронома и математика Арьябхату (476–550 гг.). И снова, как и в примере Эратосфена, до нас дошёл результат его вычислений, данный в «йоджанах», то есть в ростах человека, увеличенных в 8000 раз. Но здесь, по крайней мере, мы можем уже провести некоторую грубую оценку точности. В самом деле, полагая рост человека равным 160 сантиметрам, мы имеем йоджану равной 12,8 км и тогда для окружности Земли получится величина в 12,8 * 3300 (число, полученное Арьябхатой), или 42 240 км: довольно точное соответствие современным данным. Конечно, это определение содержит всё ту же неоднозначность: в качестве эталона у нас используется неточная и непостоянная величина, а именно рост человека. Вопросы эталонов мы также обсудим немного позже.

Из последнего примера хорошо видно, что с достаточно приемлемой точностью (приемлемой для многих целей!) размеры Земли были известны уже в начале новой эры. На попытках улучшить результаты в средние века мы здесь останавливаться не будем: они не сильно изменили предшествующие впечатляющие результаты. Пожалуй, стоит лишь упомянуть о двух вещах. Первое — это то, что экспериментально была показана «сплюснутость» Земли у полюсов. Это находилось в прекрасном соответствии с предсказанием сэра Исаака Ньютона о том, что Земля должна быть больше растянута у экватора, чем у полюсов из-за центробежной силы, возникающей при её вращении. Второе — развитие методов триангуляции, то есть измерения любых, сколь угодно больших расстояний с помощью геометрических построений, основанных на разбивке определяемого расстояния на участки, которыми являются стороны треугольников. Я снова не буду подробно останавливаться здесь на этих методах, скажу лишь, что идея здесь в том, чтобы определять неизвестные расстояния не прямым измерением, а с помощью геометрии, заменяя измерение длины на измерение углов.

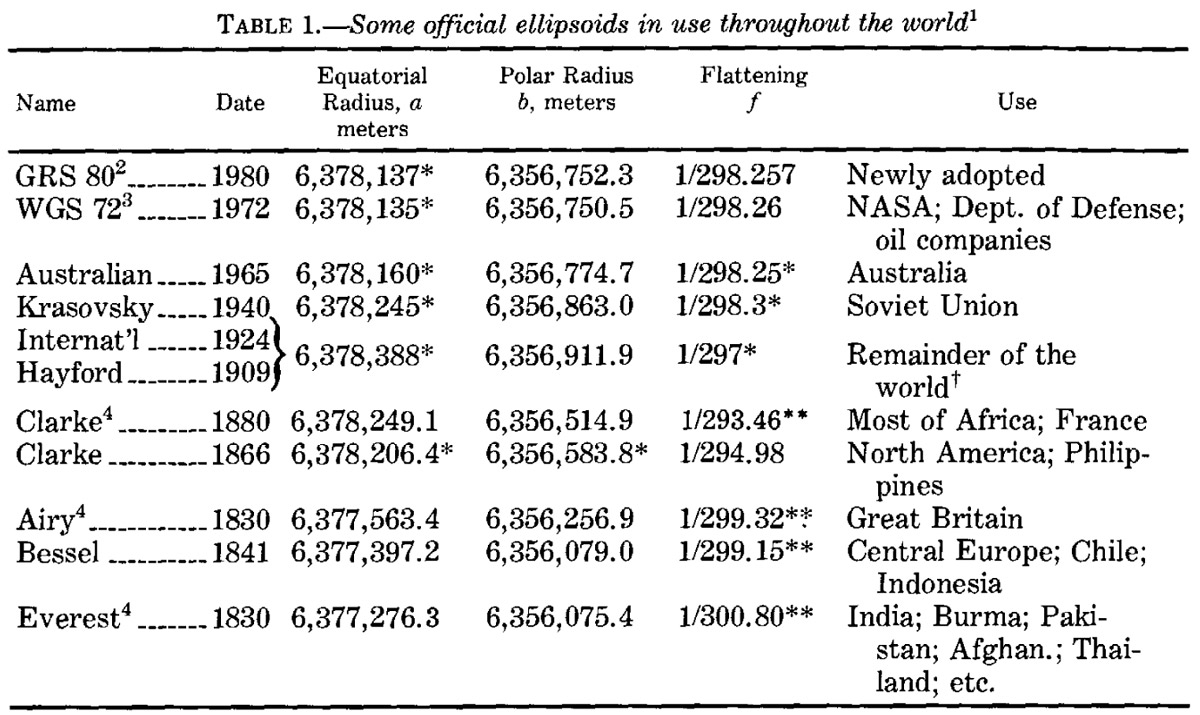
Дальнейшее продвижение в этом направлении, связанное уже с качественным скачком в точности измерений, относится уже к концу XVIII–началу XIX века. Именно в это время начался взрывной рост такого рода измерений. Кроме того, окончательно пришло понимание того, что Земля не сферична, причём не сферична достаточно сильно. Впечатляющая таблица, подводящая итог целого столетия таких измерений, приведена в учебнике В.В. Витковского «Практическая геодезия», изданном в самом начале XX века.

​

В этой табличке можно увидеть сразу несколько примечательных фактов, полезных для дальнейшего рассмотрения. Первое, что сразу же бросается в глаза — это то, что за неполное столетие большая полуось земного эллипсоида «выросла» на 2–2,5 километра! В длине окружности (точнее, эллипса, являющегося сечением земного эллипсоида) это увеличение выглядит ещё более впечатляющим: 12–15 километров. Много это или мало? На этот вопрос я постараюсь ответить чуть ниже.

Второе примечательное наблюдение — это вариации сжатия. Я снова не буду перегружать читателя лишними формулами, скажу лишь, что большая и малая полуоси эллипсоида и «сжатие» находятся во взаимно однозначном соответствии, а величина дроби варьирует в пределах нескольких процентов: именно в такой пропорции менялось представление о «сплюснутости» Земли у полюсов.

Наконец, третье наблюдение — это то, что в самой первой строчке, относящейся к измерениям Деламбра, длина четверти меридиана (в данном случае, речь идёт о Парижском меридиане), в точности равна 10 000 км. Это прямо связано с историей создания эталона метра, немного об этой истории я расскажу чуть позже.

Динамика изменений параметров земного эллипсоида становится более заметной, если посмотреть на сокращённый вариант таблицы, которая приведена в учебнике выдающегося учёного Ф.Н. Красовского «Руководство по высшей геодезии», вышедшем в 1926 году.

​

Таблица дополнена ещё двумя измерениями эллипсоида, относящимися к началу XX века. Но самая главная заслуга Ф.Н. Красовского в том, что именно им были предложены параметры ещё одного эллипсоида, который с успехом продолжает использоваться и в наши дни. Параметры эллипсоида его имени приведены в следующей таблице, взятой из популярного американского справочника 1987 года.

Из последней таблицы видно, что размеры полуосей эллипсоида начинают наконец-то сходиться к определённой величине, разница между последовательными данными становится уже меньше метра, да и параметр сжатия уже практически не меняется.

На этом месте я хочу прервать хронологический рассказ об изменениях в размерах эллипсоидов, потому что мы подошли к самой сути вопроса статьи: до какой степени точности нужно знать эти размеры и для чего это нужно?

КАКИЕ НУЖНЫ ЭЛЛИПСОИДЫ?

На самом деле, вопрос заданный в такой формулировке является довольно бессмысленным и самым правильным ответом на него будет встречный вопрос: «Для чего?»

Обратим своё внимание на последнюю табличку. В ней особняком стоят два самых поздних эллипсоида: WGS72 и GRS80. Это так называемые общеземные эллипсоиды (эллипсоида WGS84, широко используемого и в наши дни, в ней ещё нет, поскольку справочник был издан в 1987 году, и этот эллипсоид, как новейший стандарт, в ней упомянут отдельной строкой). Основной целью нахождения параметров общеземного эллипсоида является наилучшее приближение геоида по всей поверхности Земли. Отсюда непосредственно следуют два необходимых требования к нему: его ось вращения (малая полуось) должна совпадать с осью вращения Земли и центр обязательно совпадает с центром масс Земли. Между прочим, из этого, как мы увидим в дальнейшем, следует и то, что сам общеземной эллипсоид одновременно и определяет систему координат. Поверхность же эллипсоида (или, что то же самое, его полуоси и/или сжатие) определяется простым соотношением: он должен минимально отклоняться в среднем от поверхности геоида (математическое выражение для этого требования я здесь приводить не буду). Ключевым здесь является понятие «в среднем». Это значит, что для данной конкретной местности общеземной эллипсоид вовсе не обязан как можно более точно описывать земную поверхность в этом месте! Важно лишь минимальное отклонение, суммированное по всей поверхности Земли.

Задачу описания, или приближения к поверхности геоида для конкретной местности решают так называемые референц-эллипсоиды. Во всех приведённых таблицах все эллипсоиды, кроме двух последних, которые мы только что упомянули, и являются, фактически, референц-эллипсоидами. Исторически по-другому и не могло быть, вплоть до второй половины XX века измерения, направленные на создание моделей эллипсоидов, проводились, как правило, в каждой стране отдельно, случаи международной кооперации были единичны. Впрочем, некоторые эллипсоиды с успехом использовались и в разных странах, но понятно, что современной точности измерений при таком подходе достичь было сложно.

Из самой постановки задачи (точное описание конкретной местности: страны, региона и т.д.) следует смягчение требований к пространственному расположению эллипсоида относительно геоида. Действительно, есть тоже только два требования, но выраженные в гораздо менее жёсткой форме: по-прежнему минимизируются отклонения от геоида, но только для выбранной местности, и малая полуось обычно сохраняет параллельность оси вращения Земли (но уже не обязательно с ней совпадает). Понятно, что это смягчение приводит к следующим последствиям:

Вышеописанные искажения и сдвиги референц-эллипсоидов относительно общеземных подробно мы рассмотрим, когда будем рассматривать системы координат. Пока же мы уже готовы ответить на вопрос, поставленный в начале главы: для чего нужны разные виды эллипсоидов?

Ясно, что для целей картографирования стран, даже самых больших, лучше всего использовать референц-эллипсоиды (вспомните ту оговорку, которую я сделал выше о том, что общеземной эллипсоид не обязан быть одинаково хорошим приближением для всех участков Земли). Никто не мешает разработать каждой стране свой референц-эллипсоид и успешно его использовать. Действительно, разработанный ещё в СССР в 40-е годы эллипсоид Красовского с успехом используется и в наши дни и по-прежнему хорош, если не требуется особая, прецизионная точность.

Если же нам нужно строить картографические изображения всей поверхности Земли или её континентов, то тут нам не обойтись без общеземных эллипсоидов. А самое главное применение они находят в разнообразных космических применениях: для расчета параметров орбит искусственных спутников Земли, задач навигации и т.д.

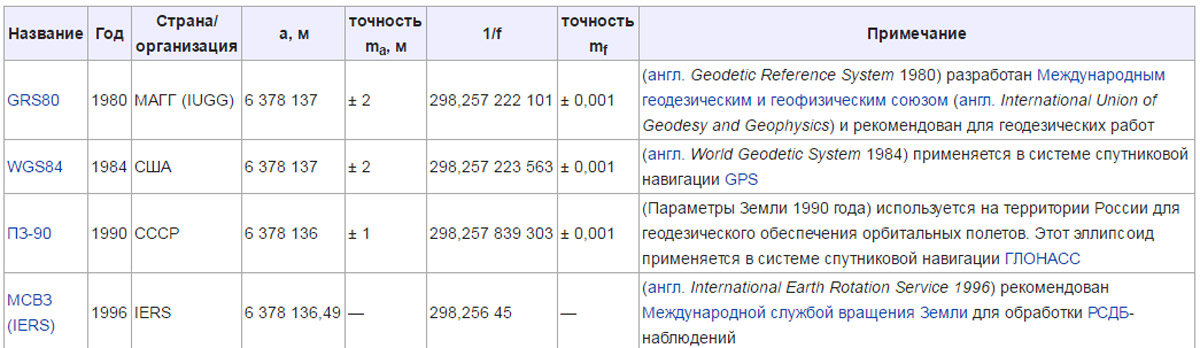
В следующей таблице приведены параметры самых современных общеземных эллипсоидов. Там же кратко обозначена основная цель его применения.

Хорошо видно, что и размеры, и сжатие эллипсоидов наконец-то практически сошлись к некоторым постоянным значениям. В самом деле, уже достигнута такая точность, что речь фактически идёт об уточнении оставшихся сантиметров полуосей (на уровне их общей величины порядка 6000 км!) и тысячных долей после запятой для параметров сжатия.

ДАВАЙТЕ ВЕРНЁМСЯ К СТАРЫМ КАРТАМ

Теперь самое время окинуть нашу обширную подборку эллипсоидов разного времени одним взглядом. Поскольку нас интересуют лишь карты, начиная от времён Российской империи до наших дней, то реальный выбор эллипсоидов у нас невелик: практически весь XIX-й век успешно использовался эллипсоид Вальбека, лишь с конца века и до 40-х годов века XX-го стал использоваться эллипсоид Бесселя. А с 40-х годов его уже сменил эллипсоид Красовского, который, как я уже упоминал, с успехом используется и в наши дни. Упомянутый в таблице эллипсоид Теннера, хотя и встречается довольно часто в литературе, по-видимому для картографических использований широкого применения не нашёл.

Легко видеть, что за время, прошедшее от времён Вальбека до Красовского большая полуось референц-эллипсоида «подросла» на 1349 м. На первый взгляд — это много, почти полтора километра. Если перевести разницу на длину «окружности» (на самом деле, эллипса) для экватора или какого-нибудь из меридианов, получим величину порядка 8,5 километров. Решительная катастрофа: представьте себе карту-километровку или близкие к ней по масштабу карты двух- и трёхвёрстки, которые «врут» на 8,5 километров!

Однако давайте теперь разберём, что значит «врать». Легко посчитать, что наши страшные 8,5 километров набегают за полную окружность, то есть за расстояние порядка 40000 км. На 40 же километров дуги окружности (порядок величины близок к характерным размерам листов, например, трёхвёрстных карт) «враньё» составит величину в тысячу раз меньшую, то есть порядка 8,5 метров. А эта величина уже меньше или равна предельной точности масштаба карты, которую мы с вами не раз обсуждали ранее!

Владимир Комиссаров

Источник