калькулятор комплексных чисел в тригонометрической форме

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Калькулятор для решения комплексных чисел.
Сумма, разность, произведение и частное комплексных чисел.
Вычислить n-ую степень и корень n-ой степени.

С помощью данного калькулятора вы можете сложить, вычесть, умножить, и разделить комплексные числа.
Программа решения комплексных чисел не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Числа в действительную или мнимую части можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так + i

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

Немного теории.

Понятие комплексного числа

Определение.
Комплексными числами называют выражения вида \(а + bi\) где \(a\) и \(a\) — действительные числа, а \(i\) — некоторый символ, для которого по определению выполняется равенство \( i^2=-1 \).

Название «комплексные» происходит от слова «составные» — по виду выражения \(а + bi\). Число \(а\) называется действительной частью комплексного числа \(а + bi\), а число \(b\) — его мнимой частью. Число \(i\) называется мнимой единицей.
Например, действительная часть комплексного числа \(2-3i\) равна \(2\), мнимая часть равна \(-3\).
Запись комплексного числа в виде \(а + bi\) называют алгебраической формой комплексного числа.

Равенство комплексных чисел

Определение.
Два комплексных числа \(a + bi\) и \(c + di\) называются равными тогда и только тогда, когда \(a =c\) и \(b =d\), т. е. когда равны их действительные и мнимые части.

Сложение и умножение комплексных чисел

Операции сложения и умножения двух комплексных чисел определяются следующим образом.

Определения.
Суммой двух комплексных чисел \(a+ bi\) и \(c + di\) называется комплексное число \( (a+c) + (b+d)i \), т.е. \( (a + bi) + (c + di) = (a + c) + (b + d)i \).

Из двух предыдущих формул следует, что сложение и умножение комплексных чисел можно выполнять по правилам действий с многочленами. Поэтому нет необходимости запоминать эти формулы, их можно получить по обычным правилам алгебры, считая, что \( i^2=-1 \).

Основные свойства сложения и умножения комплексных чисел

1. Переместительное свойство
\( z_1 + z_2 = z_2 + z_1 \),
\( z_1z_2 = z_2z_1 \)

2. Сочетательное свойство
\( (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) \),
\( (z_1z_2)z_3 = z_1(z_2z_3) \)

3. Распределительное свойство
\( z_1(z_2 + z_3) = z_1z_2 + z_1z_3 \)

Комплексно сопряженные числа

Отметим, что \( \overline = a+bi \), поэтому для любого комплексного числа \(z\) имеет место равенство
\( \overline<(\overline)> = z \)
Равенство \( \overline = z \) справедливо тогда и только тогда, когда \(z\) — действительное число.

Модуль комплексного числа

Определение.
Модулем комплексного числа \(z = a + bi\) называется число \( \sqrt \), т.е.
\( |z|=|a+bi| = \sqrt \)

Из данной формулы следует, что \( |z| \geqslant 0 \) для любого комплексного числа \(z\), причем \(|z|=0\) тогда и только тогда, когда \(z=0\), т.е. когда \(a=0\) и \(b=0\).

Вычитание комплексных чисел

Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел \(z_1\) и \(z_2\) существует, и притом только одно, число \(z\), такое, что
\( z + z_2 = z_1 \),
т.е. это уравнение имеет только один корень.

Деление комплексных чисел

Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел \( z_1 \) и \( z_2 \neq 0 \) существует, и притом только одно, число \( z \), такое, что \( z \cdot z_2=z_1 \) т.е. это уравнение относительно z имеет только один корень, который называется частным чисел \( z_1 \) и \( z_2 \) и обозначается \( z_1:z_2 \), или \( \frac \), т.е. \( z=z_1:z_2 = \frac \)

Комплексное число нельзя делить на ноль.

Частное комплексных чисел \( z_1 \) и \( z_2 \neq 0 \) можно найти по формуле
$$ \frac = \frac> <|z_2|^2>$$

Геометрическая интерпретация комплексного числа.
Комплексная плоскость

Действительные числа геометрически изображаются точками числовой прямой. Комплексное число \(a + bi\) можно рассматривать как пару действительных чисел \((a; b)\). Поэтому естественно комплексные числа изображать точками плоскости.

Пусть на плоскости задана прямоугольная система координат. Комплексное число \(z = a + bi\) изображается точкой плоскости с координатами \((a; b)\), и эта точка обозначается той же буквой \(z\).

Отметим, что точки \(z\) и \(-z\) симметричны относительно точки \(O\) (начала координат), а точки \( z \) и \( \overline \) симметричны относительно действительной оси.

Комплексное число \(z = a+bi\) можно изображать вектором с началом в точке \(O\) и концом в точке \(z\). Этот вектор будем обозначать той же буквой \(z\), длина этого вектора равна \(|z|\).

Геометрический смысл модуля комплексного числа

Выясним геометрический смысл модуля комплексного числа \(|z|\). Пусть \(z = a+bi\). Тогда по определению модуля \( |z|= \sqrt \). Это означает, что \(|z|\) — расстояние от точки \(O\) до точки \(z\).

Например, равенство \(|z| = 4\) означает, что расстояние от точки \(O\) до точки \(z\) равно \(4\). Поэтому множество всех точек \(z\), удовлетворяющих равенству \(|z| = 4\), является окружностью с центром в точке \(O\) радиуса \(4\). Уравнение \(|z| = R\) является уравнением окружности с центром в точке \(O\) радиуса \(R\), где \(R\) — заданное положительное число.

Геометрический смысл модуля разности комплексных чисел

Выясним геометрический смысл модуля разности двух комплексных чисел, т.е. \( |z_1-z_2| \).
Пусть \( z_1 = a_1+b_1i, \; z_2 = a_2+b_2i \)
Тогда \( |z_1-z_2| = |(a_1-a_2) + (b_1-b_2)i| = \sqrt <(a_1+a_2)^2 + (b_1+b_2)^2>\)

Из курса геометрии известно, что это число равно расстоянию между точками с координатами \( (a_1;b_1) \) и \( (a_2;b_2) \).

Итак, \( |z_1-z_2| \) — расстояние между точками \( z_1 \) и \( z_2 \).

Тригонометрическая форма комплексного числа. Аргумент комплексного числа

Определение
Аргумент комплексного числа \( z \neq 0 \) — это угол \( \varphi \) между положительным направлением действительной оси и вектором \(Oz\). Этот угол считается положительным, если отсчет ведется против часовой стрелки, и отрицательным при отсчете по часовой стрелке.

Связь между действительной и мнимой частями комплексного числа \(z = a + bi\), его модулем \(r=|z|\) и аргументом \( \varphi \) выражается следующими формулами:
\( \left\< \begin a=r \cos \varphi \\ b=r \sin \varphi \end \qquad (1) \right. \)

Аргумент комплексного числа \(z = a+bi\) ( \( z \neq 0 \) ) можно найти, решив систему (2). Эта система имеет бесконечно много решений вида \( \varphi =\varphi_0+2k\pi \), где \( k\in\mathbb , \;\; \varphi_0 \) — одно из решений системы (1), т.е. аргумент комплексного числа определяется неоднозначно.

Для нахождения аргумента комплексного числа \(z = a+bi\) ( \( z\neq 0 \) ) можно воспользоваться формулой
\( tg \varphi = \large \frac \normalsize \qquad (3) \)

При решении уравнения (3) нужно учитывать, в какой четверти находится точка \(z = a+bi\).

Запись комплексного числа в тригонометрической форме

Умножение и деление комплексных чисел, записанных в тригонометрической форме

С помощью тригонометрической формы записи комплексных чисел удобно находить произведение и частное комплексных чисел \(z_1\) и \(z_2\). Если два комплексных числа записаны в тригонометрической форме :
\( z_1 = r_1(\cos\varphi_1 +i\sin\varphi_1), \quad z_2 = r_2(\cos\varphi_2 +i\sin\varphi_2) \) то произведение этих комплексных чисел можно найти по формуле:
\( z_1z_2 = r_1r_2(\cos(\varphi_1+\varphi_2) +i\sin(\varphi_1+\varphi_2)) \)

Из этой формулы следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

Из этой формулы следует, что модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность аргументов делимого и делителя является аргументом частного.

Формула Муавра

Источник

Калькулятор комплексных чисел

Чтобы быстро и правильно выполнить операцию с комплексными числами, воспользуйтесь данным онлайн калькулятором, для этого необходимо:

Комплексное число z можно представить в алгебраической, тригонометрической или показательной (экспоненциальной) форме.

1. Алгебраическая запись: z = a + bi, где a и b являются вещественными числами, причем, a — действительная часть, bi — мнимая, i — мнимая единица.

2. Тригонометрическая запись: z = r (cos + i sin φ), где r — модуль комплексного числа, z — расстояние от точки на комплексной плоскости до начала координат.

Модуль комплексного числа — вещественное число |z|, равное корню квадратному из суммы квадратов вещественных чисел (a и b): r = |z| = √a 2 + b 2

Аргумент комплексного числа z — угол φ, образованный радиус-вектором точки, соответствующей комплексному числу. Значение аргумента находится в диапазоне (-π. π], для всех целых k определяется с точностью 2πk: φ = Аrg (z) = arctg (b/a). Для z, равного нулю, аргумент не определен.

3. Для сокращения Эйлер ввел Показательную запись: z = rе iφ

Действия над комплексными числами

1. Сложение: z1 + z2 = (а1 + а2) + (b1 + b2) i, где z1 = а1 + b1i; z2 = а2 + b2i. При сложении комплексных чисел складываются их реальные и мнимые части, причем, сумма не изменится от перемены мест слагаемых.

2. Вычитание: z1 — z2 = (а1 — а2) + (b1 — b2) i. При вычитании комплексных чисел вычитаются их реальные и мнимые части.

3. Умножение: z1z2 = (а1а2 — b1b2) + (а1b2 + а2b1) i, зная что i*i=-1. Умножение комплексных чисел выполняется по правилам умножения многочленов.

4. Деление: z1 / z2 = (a + bi) / (c + di) = (ac + bd) / (c2 + d2) + ((bc — ad) / (c2 + d2)) i, где z1 = a + bi; z2 = c + di. Деление выполняется путем умножения числителя и знаменателя на выражение, сопряженное знаменателю.

5. Возведение в целую степень. Для возведения комплексного числа во вторую степень можно записать степень, как произведение двух множителей и выполнить операцию умножения по правилу умножения многочленов. Для возведения комплексного числа в большую степень проще воспользоваться показательной формой: z n = r n e inφ полученной из формулы Муавра: (cos (х) + isin (х)) n = cos (nх) + isin (nх).

6. Вычисление корня n-ой степени: 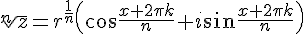, где k — целое число в диапазоне 0. n-1

Источник

Калькулятор комплексных чисел в тригонометрической форме

Понятия комплексные или мнимые числа впервые начали применяться при решении квадратных уравнений. Когда дискриминант получался меньше нуля (D Онлайн калькулятор комплексных чисел

Программа выполняет вычисления c комплексными числами, представленными в алгебраической или показательной форме, а так же рациональными числами.

Сложение и вычитание комплексных чисел необходимо осуществлять в алгебраической форме, если число представлено в иной форме, нужно перевести его в алгебраическую, воспользовавшись калькулятором, или же вручную по формулам ниже:

Умножение и деление комплексных чисел возможно реализовать как в алгебраической, так и в показательной формах. Но намного практичней осуществлять действие в показательной форме, этот способ займет намного меньше времени при расчете, например, токов короткого замыкания.

Сложение сопряженных чисел:

При делении комплексных чисел в алгебраической форме необходимо избавиться от мнимой составляющей в знаменателе. Для этого числитель и знаменатель домножают на число, сопряженное знаменателю.

Перевод чисел из алгебраической формы в показательную и наоборот возможно осуществить с помощью калькулятора для комплексных чисел, который Вы можете скачать по ссылке. Кстати, именно этим калькулятором я пользовался при расчете комплексных чисел ТОЭ, когда учился в университете. Пользоваться им крайне просто. Для перевода в разные формы используется установка нужного «флажка».

Если на руках имеется реальный калькулятор, который Вы купили в канцелярском магазине, и он обладает возможностью расчета комплексных чисел, то внимаем. Сейчас расскажу как им пользоваться.

1. Чтоб перевести комплексное число 5+3i из алгебраической формы в показательную, нажимаем клавиши в следующей последовательности:

Источник

Онлайн калькулятор для работы с комплексными числами

Не у каждого пользователя может возникнуть необходимость в вычислении комплексных чисел. При этом те, у кого она все же появляется, обязательно должны знать, что есть возможность вычислять в интернете комплексные числа, калькулятор онлайн для этого и создан. Есть множество таких сервисов, простых в использовании и доступных в любое время. В этой статье мы поговорим о наиболее популярных, и рассмотрим некоторые нюансы, которые следует учитывать в процессе работы.

Для чего используется?

Естественно, тем, кто ищет такой онлайн калькулятор, не нужно объяснять, для чего он нужен, но стоит отметить некоторые функции, с которыми он должен справляться.

Такая программа должна выполнять:

На некоторых сайтах необходимо просто ввести известные части задачи и выбрать нужную операцию из предлагаемого списка. Ниже будут представлены наиболее функциональные и удобные программы, с которыми легко работать в режиме реального времени.

Отличный онлайн калькулятор для комплексных чисел – Kontrolnaya Rabota

Данный сервис можно смело считать одним из самых надежных, он оперативно и правильно вычисляет. Работать с ним нужно так:

При необходимости детальный принцип решения найдете под ответами, для этого существует окошко «Описание». Кроме того, сайт можно использовать и для неравенств, уравнений, матриц и прочего.

OnlineMSchool

Данный ресурс очень простой и понятный, освоится сразу даже новичок за несколько секунд. Провести действия поможет следующий алгоритм:

С помощью данного ресурса вы получаете детальное описание нужного примера, позволяющее понять принцип вычисления задач с комплексными числами и закрепить пройденное. Доступен для скачивания из сервиса Гугл Плей.

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Если вам нужно решить задачи, где есть комплексные числа, калькулятор онлайн станет отличным помощником. Ресурсы, отмеченные в этой статье, очень просты в использовании. На каждом из них вам будет выдан не только ответ, но и полное описание принципа решения. Если у вас возникли какие-то вопросы, пишите в комментариях. Подписывайтесь на обновления блога, чтобы не пропустить все самое актуальное и интересное.

Источник