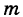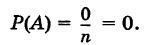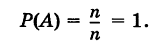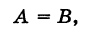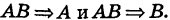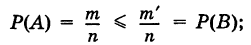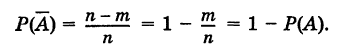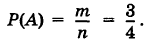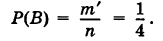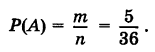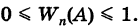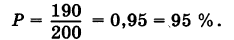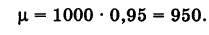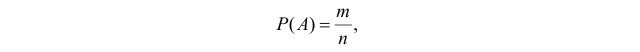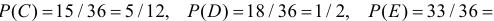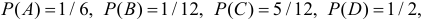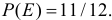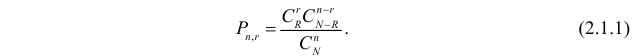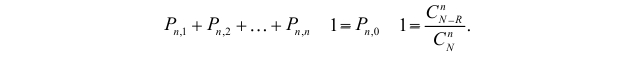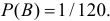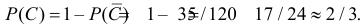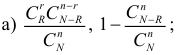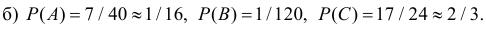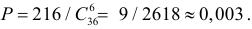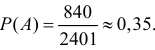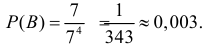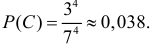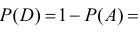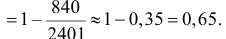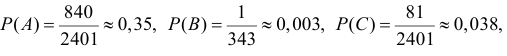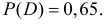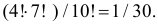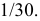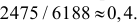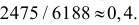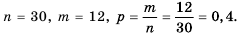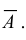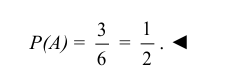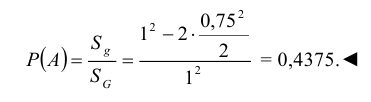классической вероятностью события а называется отношение
Теория вероятностей, формулы и примеры
Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!
Основные понятия
Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.
Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.
Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».
Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.
Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.
Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:
Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.
Формулы по теории вероятности
Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.
Случайные события. Основные формулы комбинаторики
Классическое определение вероятности
Вероятностью события A в некотором испытании называют отношение:
P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A
Таким образом, вероятность любого события удовлетворяет двойному неравенству:
Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?
Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:
Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.
Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?
Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).
Геометрическое определение вероятности
Геометрическая вероятность события А определяется отношением:
P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно
Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.
Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?
У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!
Сложение и умножение вероятностей
Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B)
Эта теорема справедлива для любого числа несовместных событий:
Если случайные события A1, A2. An образуют полную группу несовместных событий, то справедливо равенство:
Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:
P(A + B) = P(A) + P(B) − P(AB)
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:
P(AB) = P(A) * P(B)
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.
Найдем вероятности того, что формула содержится:
А — формула содержится в первом справочнике;
В — формула содержится во втором справочнике;
С — формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.
Формула полной вероятности и формула Байеса
 |
По теореме умножения вероятностей:
Аналогично, для остальных гипотез:
Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.
Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Формула Бернулли
При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.
Биномиальное распределение — распределение числа успехов (появлений события).
Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.
Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:
Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂
Наивероятнейшее число успехов
Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:
Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.
В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:
 |
Здесь λ = np обозначает среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.
События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).
При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.
Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
P1000(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.
Ответ: ориентировочно 0,18.
Теоремы Муавра-Лапласа
Кроме того, пусть Pn(k1;k2) — вероятность того, что число появлений события А находится между k1 и k2.
Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:
Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.
Содержание:
Классическое определение вероятности:
Пусть событие А — некоторый исход испытания и
— конечная система всех возможных и единственно возможных попарно несовместных элементарных исходов этого испытания (полная система элементарных событий). Таким образом, событие А происходит тогда и только тогда, когда имеют место некоторые события из системы (1) (благоприятные или благоприятствующие исходы или так называемые шансы для события А).
Предположим, что события системы (1) равновозможны, т. е. нет основания предполагать, что одно из событий системы (1) превалирует, в смысле появления, перед другими. Иногда это можно установить, используя свойство симметрии.
Определение: Под вероятностью Р(А) события А понимается отношение числа равновозможных элементарных исходов, благоприятствующих событию А> к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания.
Таким образом, если
Так как, очевидно, 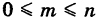
т. е. вероятность любого события есть неотрицательное число, не превышающее единицы.
Замечание. Из определения вероятности следует, что равновозможные элементарные события являются равновероятными, т. е. обладают одной и той же вероятностью.
Из определения вероятности вытекают следующие основные ее свойства.
1. Вероятность невозможного события равна нулю.
Действительно, если событие А невозможно, то число благоприятных ему элементарных исходов 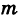
2. Вероятность достоверного события равна единице.
В самом деле, если событие А достоверно, то, очевидно, 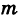
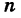
Приведем некоторые элементарные теоремы о вероятностях.
Определение: Два события А и В называются эквивалентными:
если каждое из них происходит всякий раз, когда происходит другое.
С точки зрения теории вероятностей такие события считаются равными.
Например, если в урне содержатся только белые и черные шары, то появление черного шара и появление небелого шара есть события эквивалентные.
Теорема: Эквивалентные события имеют одинаковые ве-роятности, т. е. если А = В, то
Действительно, каждый элементарный исход для события А является таковым же для события В и обратно. В силу формулы (2) справедливо равенство (4).
Определение: Говорят, что из события А следует событие 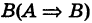
Например, для любых событий Аи В имеем
Теорема: Если 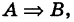
В самом деле, пусть события А и В включены в общую систему равновероятных элементарных исходов, причем 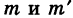
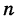
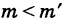
таким образом, неравенство (5) доказано.
Определение: Событие А, происходящее тогда и только тогда, когда не происходит событие А, называется противоположным последнему.
Например, если при бросании монеты событие А есть выпадение герба, то событие А представляет собой невыпадение герба, т. е. выпадение решетки.
Из определения 4 следует, что: 1) событие А + 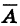
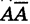
Теорема: Вероятность противоположного события 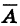
Действительно, пусть полная система равновозможных элементарных исходов содержит п событий, из которых 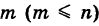

Приведем ряд примеров на непосредственное вычисление вероятностей событий.
Пример:
Монета бросается два раза. Какова вероятность: 1) выпадения герба хотя бы один раз (событие А); 2) двукратного выпадения герба (событие В)?
Решение:
Равновозможными элементарными исходами здесь являются: ГГ, ГР, РГ, РР; число их 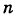
Событию А благоприятствуют исходы ГГ, ГР, РГ, число которых 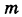
Событию В благоприятствует один исход ГГ 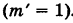
Пример:
Игральная кость бросается два раза. Какова вероятность того, что сумма выпавших очков равна 6 (событие А)?
Решение:
Равновозможными элементарными исходами здесь являются пары (х, у), где х и у принимают значения 1, 2, 3, 4, 5, 6; общее число элементарных исходов 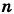
Событию А благоприятствуют пары (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), число которых 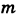
Статистическое определение вероятности:
Классическое определение вероятности события предполагает, что: 1) число элементарных исходов конечно; 2) эти исходы равновозможны.
Однако на практике встречаются испытания с бесконечным числом различных возможных исходов. Кроме того, нет общих методов, позволяющих результат испытания, даже с конечным числом исходов, представить в виде суммы равновозможных элементарных исходов.
Поэтому применение классического определения вероятности весьма ограниченно.
Мы укажем сейчас другое определение вероятности, иногда более удобное для приложений.
Пусть производится п однотипных испытаний, одним из исходов которых является данное событие А.
Определение: Отношение числа появлений тп события А к общему числу испытаний п называется относительной частотой (частостью) события А.
Таким образом, обозначая через Wn (А) относительную частоту события А при 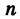
Очевидно,
Из формулы (1) получаем
т. е. число появлений события А равно его относительной частоте умноженной на число испытаний.
При однотипных массовых испытаниях во многих случаях наблюдается устойчивость относительной частоты события, т. е. при числе испытаний 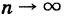
Определение: Под вероятностью события в статистическом смысле понимается почти достоверный предел его относительной частоты при неограниченно растущем числе испытаний.
Таким образом, почти достоверно, что относительная частота события приближенно совпадает с его статистической вероятностью, если число испытаний достаточно велико.
С этой точки зрения величина
представляет собой среднее значение числа появления события А при п испытаниях.
При широких предположениях доказывается, что вероятности события в классическом и статистическом смыслах совпадают между собой.
Пример:
В результате ряда испытаний было обнаружено, что при 200 выстрелах стрелок попадает в цель в среднем 190 раз. Какова вероятность р поражения цели этим стрелком? Сколько для него попаданий в цель можно ожидать при 1000 выстрелов?
Решение:
Используя статистическое определение вероятности, имеем
Отсюда число удачных выстрелов из 1000 выстрелов примерно составляет
Классическое определение вероятности (Формула)
Классическое определение вероятности. Если исходы опыта равновозможны, то вероятностью события A называется отношение числа исходов, благоприятствующих данному событию, к числу всех возможных исходов опыта, т.е.
где 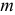
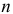
Свойства вероятностей
Если вероятность интересующего нас события A по каким-либо причинам вычислить трудно, то можно попытаться вычислить вероятность противоположного события, а затем с помощью свойства 3 вычислить искомую вероятность события A.
Пример №1
Брошены две игральные кости. Найти вероятности следующих событий:
A – на обеих костях выпало одинаковое число очков;
B – сумма числа очков не меньше 11;
C – число очков на первой кости больше, чем на второй;
D – сумма очков четная;
E – сумма числа очков больше трех.
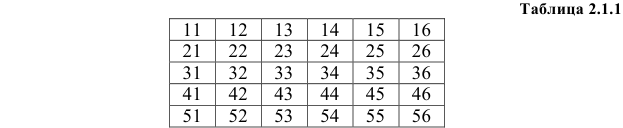
Решение. Число очков, благоприятствующих каждому из названных событий, легко подсчитать, если все возможные исходы опыта перечислить в виде табл. 2.1.1. В каждой клетке таблицы первая цифра указывает число очков на первой кости, вторая –– на второй кости.
Если кости симметричны и однородны, то все перечисленные исходы опыта равновозможны. Тогда 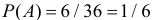
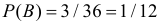
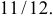
Ответ.
Пример №2
а) В урне содержится N шаров, из них R красного цвета. Наугад выбрано 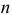
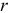
б) Из партии, содержащей 10 изделий, среди которых три бракованных, наугад извлекаются три изделия для контроля. Найти вероятности следующих событий:
A – среди выбранных изделий ровно два бракованных;
B – выбраны только бракованные изделия;
С – среди выбранных изделий содержится хотя бы одно бракованное.
Решение. а) Если шары тщательно перемешаны и выбираются наугад, то равновозможен выбор любых 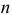
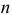
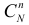
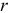
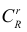
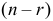
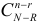
Пусть 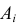
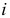
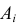
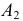
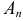
б) Выбрать любых три изделия из 10 можно 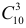
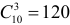
Событию A благоприятствуют те исходы, при которых из семи годных изделий выбирается одно (это можно сделать 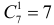
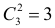
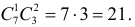
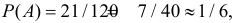
Вероятность события 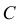
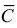
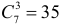
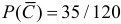
Ответ.
Пример №3
При раздаче тщательно перемешанных карт (в колоде 36 карт) игрок получает шесть карт. Какова вероятность того, что игрок получит два туза, два короля и две дамы любой масти?
Решение. Шесть карт данному игроку можно сдать 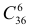
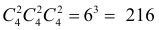
Ответ. 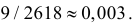
Пример №4
В течение недели независимо друг от друга происходят четыре события. Найдите вероятности следующих событий:
A – все четыре события произойдут в разные дни недели;
B – все четыре события произойдут в один день;
C – все эти события произойдут в последние три дня недели;
D – хотя бы в один день недели произойдут два или более из этих событий.
Решение. Дни недели можно представить в виде ящиков, а события в виде шариков. Тогда распределение событий по дням недели можно считать раскладкой шариков по ящикам. Так как каждый из четырех шариков можно поместить в любой из семи ящиков, то существует 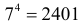
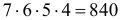
Поэтому
Событию B благоприятствует всего семь способов. Поэтому
Все четыре события могут произойти в последние три дня недели 3 4 способами. Поэтому
Событие D противоположно событию A. Поэтому
Ответ.
Пример №5
10 книг, из которых четыре имеют красный переплет, наугад ставят на полку. В предположении, что все расстановки книг на полке равновозможны, найти вероятность того, что книги с красными переплетами окажутся стоящими подряд.
10 книг можно на полке расставить 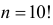
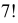
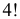
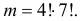
Ответ.
Замечание. Пусть 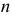
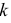
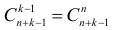
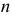
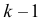
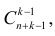
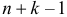
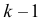
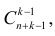
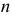
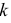
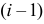
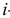
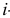
Пример №6
Случайным образом 12 одинаковых шаров размещаются в шести ящиках. Какова вероятность того, что ровно два ящика останутся пустыми?
Решение. Согласно предыдущему замечанию распределить 12 шаров по шести ящикам можно 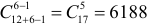
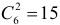
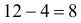
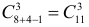
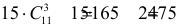
Ответ.
Классическое определение вероятности и решение задач
Пример №7
В ящике лежат два шара: белый и черный. Из ящика наугад вынимают один шар.
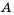
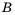
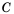
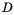
Как известно из предыдущего параграфа, событие 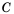
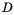
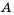
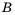
Эту вероятность получим, если количество белых шаров, то есть 1, разделим на количество всех шаров 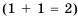
Сформулируем классическое определение вероятности:
вероятность случайного события 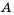
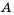
В виде формулы это определение можно записать так:
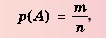
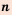
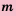

Иногда вероятность представляют в процентах, тогда 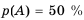
Возвращаясь к примеру 1, можно легко найти вероятности событий 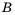
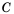
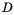
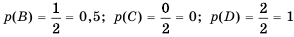
Таким образом, приходим к важному выводу:
вероятность достоверного события равна 1, вероятность невозможного события равна 0; вероятность случайного события равна любому числу от 0 до 1.
Вероятности событий 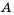
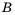
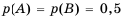
Равновероятные события — события, вероятность которых одинакова в данном испытании.
Рассмотрим еще примеры.
Пример №8
Из 30 учеников класса 12 имеют по алгебре оценки высокого уровня. Какова вероятность того, что наугад выбранный учащийся этого класса имеет по алгебре оценку высокого уровня?
Решение:
Имеем:
Пример №9
Одновременно бросили два игральных кубика. Какова вероятность того, что сумма выпавших очков:
1) равна 6; 2) меньше 5?
Решение:
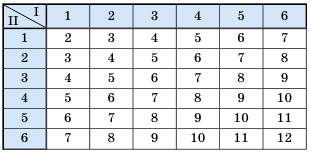
Составим таблицу суммы очков, которые могут выпасть на двух игральных кубиках, брошенных одновременно. 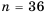
1) Имеем 5 случаев, когда сумма очков на обоих кубиках равна 6, поэтому 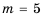
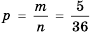
2) Имеем 6 случаев, когда сумма очков на обоих кубиках меньше чем 5. Поэтому 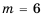
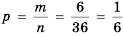
Ответ. 1) 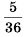
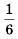
Пример №10
1) равна 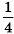
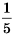
Решение:
Пусть в коробке 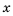
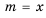
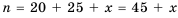
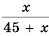
1) По условию- 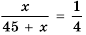
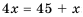
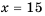
2) По условию- 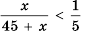
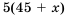
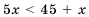
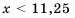
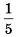
Ответ. 1) 15; 2) не более 11.
Пример №11
Владелец мобильного телефона забыл две последние цифры своего PIN-кода, но помнит, что они разные. Найти вероятность того, что он разблокирует телефон с первой попытки.
Решение:
Ответ.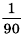
Классификация событий
Одним из основных понятий теории вероятностей является понятие события.
Событием называется любой факт, который в результате испытания может произойти или не произойти.
Под испытанием (опытом, экспериментом) в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
События принято обозначать прописными буквами латинского алфавита: А, В, С и т.д.
Событие называется достоверным, если в результате испытания оно обязательно должно произойти. Событие называется случайным, если в результате испытания оно может либо произойти, либо не произойти. Событие называется невозможным, если в результате испытания оно вообще не может произойти.
События называются несовместными, если наступление одного из них исключает появление любого другого. В противном случае события называются совместными.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
Например, два студента пришли сдавать зачет. Обязательно произойдет одно из следующих событий: оба студента сдадут зачет (событие А), только один студент сдаст зачет (событие В), ни один из студентов не сдаст зачет (событие С). События А, В, С являются единственно возможными.
События называются равновозможными, если по условиям симметрии есть основания считать, что ни одно из этих событий не является объективно более возможным, чем другие.
Например, появление герба или решки при бросании монеты есть события равновозможные. Действительно, предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму, и наличие чеканки не оказывает влияния на выпадение той или иной стороны монеты.
Несколько событий образуют полную группу, если они являются единственно возможными и несовместными исходами испытания. Это означает, что в результате испытания должно произойти одно и только одно из этих событий.
Например, студент отвечает на вопросы экзаменационного билета. Билет содержит два вопроса. Возможны следующие исходы испытания: студент ответит на оба вопроса (событие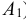
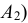
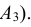
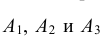
Противоположными называют два единственно возможных события, образующих полную группу.
Например, событие, состоящее в том, что студент в данный момент находится в аудитории, и событие, состоящее в том, что он находится вне аудитории, являются противоположными.
Если одно из двух противоположных событий обозначено через А, то другое принято обозначать
Классическое и статистическое определение вероятности
Для практической деятельности необходимо уметь сравнивать события по степени возможности их наступления. Рассмотрим классический случай. В урне находится 10 шаров, 8 из них белого цвета, 2 черного. Очевидно, что событие «из урны будет извлечен шар белого цвета» и событие «из урны будет извлечен шар черного цвета» обладают разной степенью возможности их наступления.
Поэтому для сравнения событий нужна определенная количественная мера. Количественной мерой возможности наступления события является вероятность. Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Классическое определение вероятности связано с понятием благоприятствующего исхода. Остановимся на этом подробнее. Пусть исходы некоторого испытания образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Такие исходы называют элементарными исходами, или случаями. При этом говорят, что испытание сводится к схеме случаев или «схеме урн», т.к. любую вероятностную задачу для подобного испытания можно заменить эквивалентной задачей с урнами и шарами разных цветов.
Исход называется благоприятствующим событию А, если появление этого случая влечет за собой появление события А.
Согласно классическому определению вероятность события А равна отношению числа исходов, благоприятствующих этому событию, к общему числу исходов, т.е. 
Пример №12
При бросании игральной кости возможны шесть исходов – выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления четного числа очков?
Решение:
Исходя из классического определения вероятности события, отметим ее свойства:
Как было сказано ранее, классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытаний, обладающих симметрией возможных исходов, т.е. сводящихся к схеме случаев. Однако существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения.
Например, если допустить, что монета сплющена, то очевидно, что события «появление герба» и «появление решки» нельзя считать равновозможными. Поэтому формула для определения вероятности по классической схеме в данном случае неприменима.
Однако существует другой подход при оценке вероятности событий, основанный на том, насколько часто будет появляться данное событие в произведенных испытаниях. В этом случае используется статистическое определение вероятности.
Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.
В отличие от математической вероятности Р(А), рассматриваемой в классическом определении, статистическая вероятность Р*(А) является характеристикой опытной, экспериментальной. Иначе говоря, статистической вероятностью события А называется число, относительно которого стабилизируется (устанавливается) относительная частота w(A) при неограниченном увеличении числа испытаний, проводимых при одном и том же комплексе условий.
Например, когда про стрелка говорят, что он попадает в цель с вероятностью 0,95, то это означает, что из сотни выстрелов, произведенных им при определенных условиях (одна и та же цель на том же расстоянии, та же винтовка и т.д.), в среднем бывает примерно 95 удачных. Естественно, не в каждой сотне будет 95 удачных выстрелов, иногда их будет меньше, иногда больше, но в среднем при многократном повторении стрельбы в тех же условиях этот процент попаданий будет оставаться неизменным. Цифра 0,95, служащая показателем мастерства стрелка, обычно очень устойчива, т.е. процент попаданий в большинстве стрельб будет для данного стрелка почти один и тот же, лишь в редких случаях отклоняясь сколько-нибудь значительно от своего среднего значения.
Еще одним недостатком классического определения вероятности (1.1), ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания. В некоторых случаях этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).
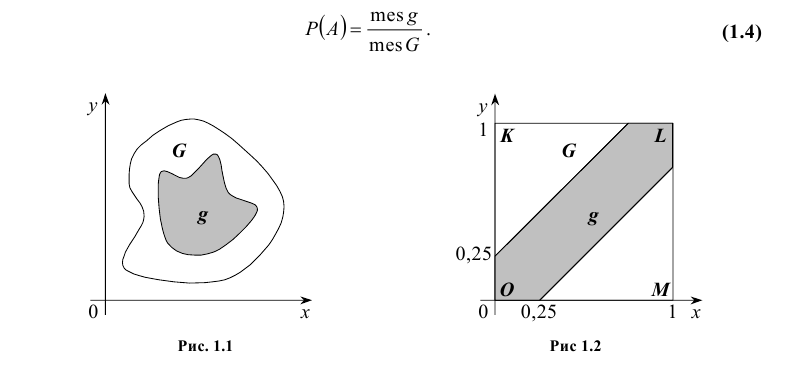
Пусть плоская фигура g составляет часть плоской фигуры G (рис. 1.1). На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении попадания на нее брошенной случайной точки.
где 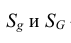
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок), двумерной (плоская фигура) или трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е.
Пример №13
Два студента условились встретиться в определенном месте между 10 и 11 часами дня. Пришедший первым ждет второго в течение 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода между 10 и 11 часами.
Решение:
Решение этого неравенства есть полоса 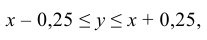
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.