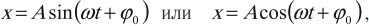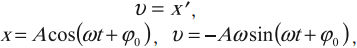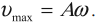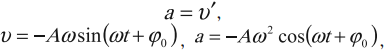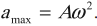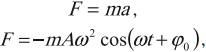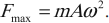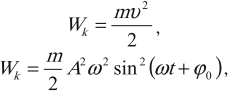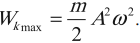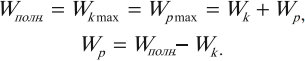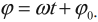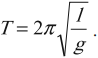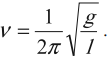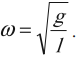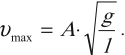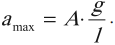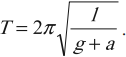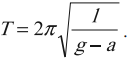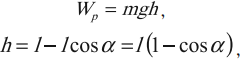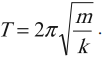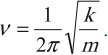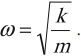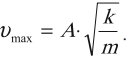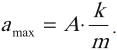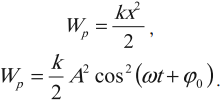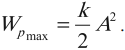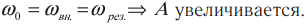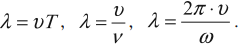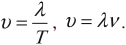колебания протекающие за счет действия внутренних сил

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

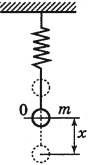
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

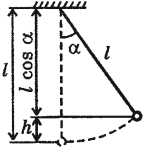
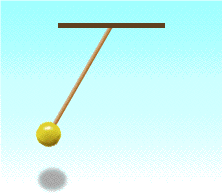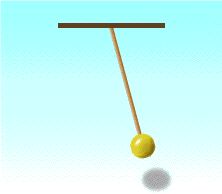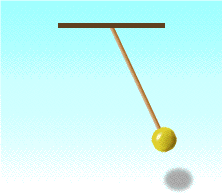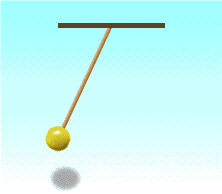
Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s», окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω₀ t (или x = x_m sin ω₀ t), х_m — амплитуда колебания, ω₀ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω₀ t (или x = x_m sin ω₀ t)), получим выражение для скорости:

где a_m = ω 2 ₀ x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

Источник

Механические колебания. Свободные и вынужденные колебания. Резонанс. Превращение энергии …

Механические колебания – это движения, которые точно или приблизительно повторяются через определенные интервалы времени. (например, колебание ветки на дереве, маятника часов, автомобиля на рессорах и так далее)

Колебания бывают свободными и вынужденными.

Колебания, совершаемые телами под действием внешних периодически изменяющихся сил, называются вынужденными (например: колебание металлической заготовки при работе кузнеца молотом).

Условия возникновения свободных колебаний :

В реальных колебательных системах всегда происходят потери энергии при свободных колебаниях. Механическая энергия расходуется на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, затем колебания прекращаются. Колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления, называются затухающими.

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Любое колебание характеризуется:

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний ().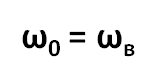

Явление резонанса учитывается в акустике, радиотехнике и технике. В строительстве, например, при сооружении мостов и других сооружений, которые подвержены механическим колебаниям и действию внешней силы.

Существует несколько колебательных систем – математический маятник (шарик на тонкой длинной нити) и пружинный маятник (тело на пружине).

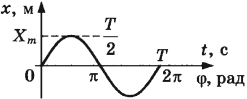
Самый простой вид колебательного движения — гармонические колебания, при которых физическая величина периодически изменяется со временем по закону синуса или косинуса (рис.).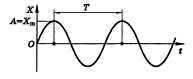При гармонических колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно :

… Е_кин → Е_р → Е_кин →…

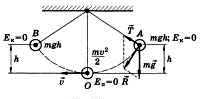
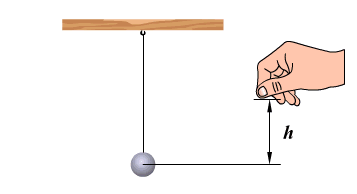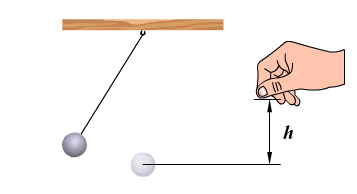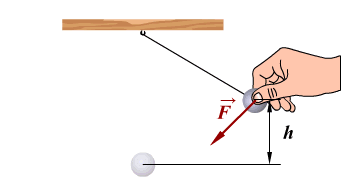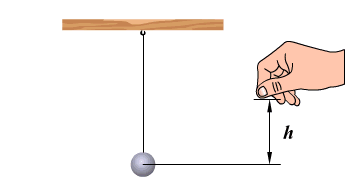
На примере колебаний тела на нити видим превращение энергии. В 1 положении наблюдаем равновесие колебательной системы. Скорость и, следовательно, кинетическая энергия тела максимальны. При отклонении маятника от положения равновесия он поднимается на высоту h относительно нулевого уровня, следовательно, в точке А маятник обладает потенциальной энергией Е_р. При движении к положению равновесия, к точке О, уменьшается высота до нуля, а скорость груза увеличивается, и в точке О вся потенциальная энергия Е_р превратится в кинетическую энергию Е_кин. В положении равновесия кинетическая энергия имеет максимальное значение, а потенциальная энергия минимальна. После прохождения положения равновесия по инерции происходит превращение кинетической энергии в потенциальную, скорость маятника уменьшается и при максимальном 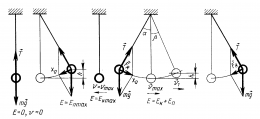отклонении от положения равновесия становится равной нулю. Е_кин = 0, Е_р = max

Закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной: Е_кин = Е_р = const

Источник

Колебания протекающие за счет действия внутренних сил

В современной физике существует специальный раздел — физика колебаний, которая занимается исследованием вибраций машин и механизмов.

Механические колебания

Механические колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Примеры колебаний: движения поршней в двигателе автомобиля, поплавка на волне, ветки дерева на ветру.

Если движение повторяется точно, то такое движение называется периодическим.

Что является характерным признаком колебательного движения?
При колебаниях движения тела повторяются.
Так, маятник, совершив один цикл колебаний, вновь совершает такой же цикл и т.д.

Маятником называют подвешенное на нити или закрепленное на оси тело, которое может совершать колебания под действием силы тяжести Земли.

Колебания бывают свободными, затухающими и вынужденными.

Свободные колебания.

Свободными колебаниями называются колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия и предоставлена затем самой себе.

Примеры свободных колебаний: колебания груза, прикрепленного к пружине, или груза, подвешенного на нити.

Затухающие колебания.

После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил.
Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления.
Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.

Вынужденные колебания.

Для того чтобы колебания не затухали, на тела системы должна действовать периодически изменяющаяся сила.
Постоянная сила не может поддерживать колебания, так как под действием этой силы может измениться только положение равновесия, относительно которого происходят колебания.

Вынужденными колебаниями называются колебания тел под действием внешних периодически изменяющихся сил.

Наибольшее значение в технике имеют вынужденные колебания.

Источник

Механические колебания и волны

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Отличительными признаками колебательного движения являются:

Для существования механических колебаний необходимо:

Механические волны – это процесс распространения колебаний в упругой среде.

Виды волн

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.

Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

где ​ \( x \) ​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​ \( A \) ​ – амплитуда колебаний; ​ \( \omega t+\varphi_0 \) ​ – фаза колебаний; ​ \( \omega \) ​ – циклическая частота; ​ \( \varphi_0 \) ​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

где ​ \( v \) ​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

где ​ \( a \) ​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ​ \( F \) ​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где ​ \( W_k \) ​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

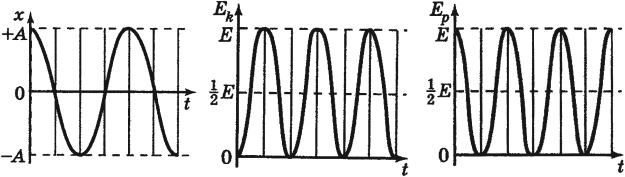
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:

При максимальном отклонении от положения равновесия:

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Амплитуда и фаза колебаний

Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ​ \( A\, (X_) \) ​, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ​ \( \varphi \) ​, единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
​ \( \varphi_0 \) ​ – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период колебаний

Период колебаний – это время одного полного колебания.
Обозначение – ​ \( T \) ​, единицы измерения – с.

Период гармонических колебаний – постоянная величина.

Частота колебаний

1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ​ \( \omega \) ​, единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

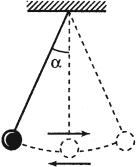
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.

Период колебаний математического маятника:

Частота колебаний математического маятника:

Циклическая частота колебаний математического маятника:

Максимальное значение скорости колебаний математического маятника:

Максимальное значение ускорения колебаний математического маятника:

Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:

Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:

Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:

Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ​ \( h \) ​, определяется по формуле:

где ​ \( l \) ​ – длина нити, ​ \( \alpha \) ​ – угол отклонения от вертикали.

Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.

Период колебаний пружинного маятника:

Частота колебаний пружинного маятника:

Циклическая частота колебаний пружинного маятника:

Максимальное значение скорости колебаний пружинного маятника:

Максимальное значение ускорения колебаний пружинного маятника:

Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:

Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.

Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.

Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.

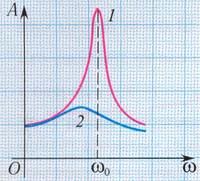
Резонанс

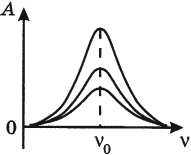
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.

​ \( v_0 \) ​ – собственная частота колебаний маятника.

На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.

Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.

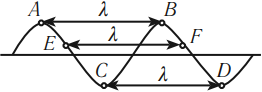
Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ​ \( \lambda \) ​, единицы измерения – м.

Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.

Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.

Источник