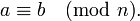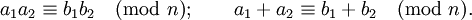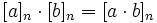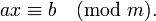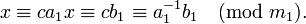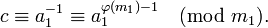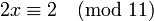кольцо вычетов по модулю натурального числа

30.04.202307.05.2023 admin 0 Комментариев

Кольцо вычетов

Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.

В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.

Содержание

Определения

Утверждение « a и b сравнимы по модулю n » записывается в виде:

Свойства

Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если

Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: , однако, сократив на 2, мы получаем ошибочное сравнение: . Правила сокращения для сравнений следующие.

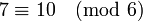
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.

Классы вычетов

Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел , то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается или .

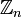
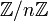
Операции сложения и умножения на индуцируют соответствующие операции на множестве :

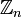
[a]_n + [b]_n = [a + b]_n

Относительно этих операций множество 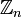является конечным кольцом, а если n простое — конечным полем.

Решение сравнений

Сравнения первой степени

В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:

Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:

Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:

Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: 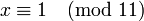, эквивалентное двум решениям по модулю 22: .

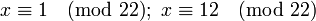
Сравнения второй степени

Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.

История

В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.

Ссылки

Полезное

Смотреть что такое «Кольцо вычетов» в других словарях:

Кольцо (алгебра) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия

Кольцо (множество) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия

Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия

Кольцо алгебраическое — Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия

Кольцо — алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия

Кольцо когомологий — Гомология одно из основных понятий алгебраической топологии. Замкнутая линия гомологична нулю, если она ограничивает кусок поверхности, который отделяется от неё, если мы произведём разрез по этой линии. Например, на сфере любая замкнутая линия… … Википедия

Мультипликативная группа кольца вычетов — Приведённая система вычетов по модулю m множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) функция Эйлера. В качестве приведённой системы вычетов… … Википедия

АНАЛИТИЧЕСКОЕ КОЛЬЦО — кольцо ростков аналитич. функций в точке аналитического пространства. Более точно: пусть kесть поле с нетривиальным абсолютным значением (обычно предполагаемое полным) и есть fc алгебра степенных рядов от с коэффициентами в k, сходящихся в нек… … Математическая энциклопедия

ЛОКАЛЬНОЕ КОЛЬЦО — коммутативное кольцо с единицей, имеющее единственный максимальный идеал. Если А Л. к. с максимальным идеалом то факторкольцо является полем и наз. полем вычетов Л. к. А. Примеры Л. к. Любое поле или кольцо нормирования является локальным.… … Математическая энциклопедия

ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО — дискретно нормированное кольцо, кольцо с дискретным нормированием, т. е. область целостности с единицей, в к рой существует такой элемент я, что любой ненулевой идеал порождается нек рой степенью элемента я; такой элемент наз. униформизирующим и… … Математическая энциклопедия

Источник

Модель натурального числа II

Структура конечного кольца вычетов по составному модулю

Замысел работы. Создать такую математическую модель большого числа, которая позволила бы находить его делители, исключая схему перебора возможных их вариантов. При построении модели полагаем известными все ее элементы: значение N = dмdб, позицию его в контуре натурального ряда чисел (НРЧ), оба делителя, их свойства.

Определяемыми неизвестными характеристиками такой универсальной модели являются функциональные зависимости одних переменных модели от других. Эти зависимости должны иметь характер законов и выполняться всегда (для всех чисел) независимо от масштаба чисел. Формирование работоспособной модели числа оказалось достаточно сложным и объемным процессом, поэтому принято решение разбить его на 2 статьи (Часть I здесь).

В настоящее время ситуация с моделированием чисел и факторизацией как пишут Манин и Панчишкин близка к тупику или уже в тупике.

В этой статье на основе закона распределения делителей (ЗРД см.здесь ) числа рассматривается вопрос о структуре конечного числового кольца вычетов (КЧКВ) и о том, как неизвестные нам делители N управляют возникновением полных квадратов — квадратичных вычетов (КВВ) в списке квадратичных вычетов, которые доступны нашему наблюдению. Часть понятий и определений вводилась в части I и здесь повторяются не все из них.

Тривиальные области списочной многострочной модели (СММ) нечетного числа

Будем рассматривать натуральный ряд чисел с добавленным слева нулевым элементом и считать, что его элементы размещены в ячейках регистра бесконечной длины. Для каждого элемента хо вычисляется квадрат, помещаемый в ячейку с таким же номером ленты другого бесконечного регистра с заливкой желтого цвета (рис.1). Если же задать составное нечетное натуральное число (СННЧ) N в качестве модуля конечного числового кольца вычетов, то лента с квадратами преобразуется.

В ее ячейки будут включены не просто квадраты (хо), а квадратичные вычеты чисел r_л ≡ хо 2 (mod N) по модулю этого составного числа N=dмdб. Для ячеек двух этих регистровых полос будет выполняться условие комплементарности. При этом мы ограничиваемся рассмотрением лишь фрагмента НРЧ от 0 до N — 1.

Добавление к фрагменту слева нулевого элемента и введение операций (+) и (·) превращает его в конечное числовое кольцо вычетов по модулю N. Если квадратичный вычет получает значение полного квадрата, то КВВ обозначается — квадратичный вычет квадрат (КВК).

Введем несколько определений.

r_л≡хо 2 (modN)≡x1 2 (modN)-квадратичный вычет левый;
х1 = N — xо — дополнение хо до модуля;
хо — текущий номер строки СММ;
t=х1 — хо =t1 + tо — разность слагаемых строки; раскладывается в сумму смежных;
p =t1tо — произведение смежных слагаемых;
r_с ≡ ¼(t 2 –1)(mod N) =t1tо(modN); средний вычет в строке;
t_пi = 2xоi — 1; нечетное число; сумма номеров смежных строк;
r_п ≡х1хо(modN=N — r_л — произведение слагаемых; правый вычет в строке.

Определение. (ТКВК) Тривиальной областью строк СМ-модели называется начальное множество строк списка, следующих подряд, содержащих в качестве r_л (левого КВВ) монотонно возрастающие полные квадраты.

Определение. Границей ТКВК (левый 1-й верхний порог) называется наибольший КВК – полный квадрат, не превышающий составного модуля N, например, для N =34999, граница ТКВК
r_лmax ≡ √N (mod N) = √34999 = 187.
Извлекаемые квадратные корни округляются до целых значений.

Определение. (ТССС) Тривиальной областью строк СМ-модели (внизу списка) называется множество строк конца списка, следующих снизу вверх подряд, содержащих монотонно возрастающие разности нечетных чисел
t = x1-xо от 1 до границы (порога), а в качестве вычетов r_с (полные квадраты за вычетом первой степени) и обладающие свойством сохранять смежность сомножителей (ССС).

Рисунок 1 — фрагмент НРЧ, реализующий конечное числовое кольцо вычетов по модулю N

Тип модели

Под типом модели будем понимать степень различия (разность) делителей модуля N. Если в области строк ТКВК имеет место пересечение (строки, содержащие левые и правые вычеты из тривиальных областей) одной или более строк с тривиальной областью ТССС, то это первый тип моделей (рабочий), если пересечение пусто, то это модели второго типа.

К первому типу относятся все RSA-числа и многие другие, в которых значения делителей с одной стороны не являются близкими, а с другой — не очень удаленными друг от друга на числовой оси НРЧ. Поясним сформулированные условия.

Числа N в СММ могут существенно различаться не только своими значениями, но и делителями. Сами делители также могут иметь различия (малые и большие значения) при близких значениях их произведений, т.е. N1 и N2 близки, а их делители N1 = 11·1129 = 12419 существенно различаются на 1129 – 11 = 1118 или N2 = 101·123 = 12423 всего на 123 – 101 = 22 единицы.

Числа, включающие в качестве делителей квадраты, имеют свои особенности. Указанные различия проявляются специфически в СМ-моделях и всегда желательно учитывать такую специфику N.

Например, в канонической СМ-модели (N = a(a+2) близнецы) дублируемые КВК следуют смежными парами, сумма первых степеней которых постоянна и равна среднему числу (a + 1).

Пример 1. (Делители числа значительно удалены друг от друга). Пусть N = 31·1129 = 34999; это число удовлетворяет основной теореме факторизации N = 34999 = 19 +30·1166.
rс(1) = 26250 = 3·rл(0) = 3·8750, контур НРЧ 34999 +35001 = 70000 с номером kп =70000:8 = 8750, инвариант N равен kп/2 = 4375, отсюда интервал для N содержит слагаемых 31 и среднее слагаемое равно dб = 1129, меньшее число tпм= 1 + dб – dм = 1+1129 –31 =1099 и большее число интервала tпб= dб + dм – 1= 1129 + 31–1 = 1159; действительно,
15(tпм+ tпб) + dб =15·2258 +1129 = 34999.

В этой точке с использованием закона распределения делителей (ЗРД) определяются делители:
dм·25 = 952 – 177 = 775 = 31·25;
dб = 952 + 177 = 1129.

Рассмотрим поведение КВВ (всего имеется 187 КВК), дублирующих (181 КВК) тривиальной области списка. Квадрат числа 31 и квадраты его кратных не дублируются, так как число 31 является делителем N.
Определение. Аттрактором (притягивающим к себе квадраты элементом НРЧ) будем называть точку (клетку) НРЧ, соответствующую значению кратному dб.

Распределение КВК до середины списка обладает определенной регулярностью, КВК группируются по 12 строк с интервалом между ними 31 позиция, и интервал между группами строк равен 797 либо 766 строк. Это следует из анализа таблиц. Существует 15 групп с 1 по 15. В пределах групп возникают аттракторы, строки как бы притягивающие к себе полные квадраты КВК-дубли. Аналогичная ситуация имеет место и для 2-й половины списка.

Определение. Областью аттрактора назовем множество точек в окрестности аттрактора, значения квадратичных вычетов которых содержат КВК, не превышающие границы тривиальной области ТКВК.

Для более ясного представления и понимания как все устроено с делителями N в НРЧ вначале будем рассматривать картину хорошо разделяемых областей аттракторов. Текст будем сопровождать числовым примером, в котором роль модуля играет полупростое число
N =31·1129 = 34999. Следовательно, аттракторами будут точки кратные dб (числа: 1·1129, 2·1129 = 2258, 3·1129 =3387, …, 15·1129) и их дополнения до модуля для 2-й половины списка.

Клетка, выделенная заливкой зеленого цвета — инволюция КЧКВ. Желтым цветом в полосе выделены КВК для каждого аттрактора. Соединения полосы переменной хо (без заливки) не везде показаны (не загромождают рисунок), но фактически имеют место, являются сплошной лентой.

Пока хо малы (левая желтая колонка верхней части таблицы) их квадраты 187 штук (хо 2 2 –1)(mod N), где
t = х1 – хо = N – 2хо разность значений, также порождает ещё одну другую тривиальную область значений переменной (r_с), обозначаемую (ТССС).

ТССС – область строк модели, содержащая вычеты (r_с), которые следуют в возрастающем порядке и представляют собой вычеты, со свойством после приведения по модулю (после редукции) сохранять смежность сомножителей. По аналогии с первой тривиальной областью для (r_л) значения из области ТССС также повторяются (дублируются) в других точках хо при продолжении преобразований списка нечетных чисел.

Эта область также характеризуется порогом, при превышении которого произведение смежных слагаемых редуцируется и результат (уменьшенное значение) уже чаще не сохраняет смежность меньших сомножителей, чем сохраняет. При сохранении свойства говорят средний вычет имеет свойство ССС- сохранение смежности сомножителей.

Устройство моделей натурального ряда чисел (НРЧ) и отдельного составного нечетного натурального числа (СННЧ) можно представить разными математическими зависимостями. Каждая из моделей ее автором ориентируется, приспосабливается к конкретной задаче или группе задач, представляющих интерес для исследования. Здесь будем рассматривать списочную многострочную модель (СММ) составного натурального числа
N = dm·dб.

На числовой оси с шагом, равным большему делителю dб, размечаются точки (позиции): dб, 2dб, 3dб, …, dм·dб – аттракторы. После этого аналогичную разметку выполняем для меньшего делителя dm. Последняя точка в обоих случаях совпадает с N.

Между размеченными с разным шагом точками возникает множество интервалов разной длины четной и нечетной, среди которых имеются такие интервалы, которые называются решающими, задачу разложения числа N на множители, так как именно они обеспечивают нахождение делителей составного модуля КЧКВ
N = dм·dб.

В соответствии с законом распределения делителей (ЗРД) решающий задачу факторизации больших чисел (ЗФБЧ) интервал своими границами [Гл, Гп] должен иметь точки кратные разным делителям N.

Поскольку относительно произвольной точки кратной dб группируются точки кратные dm с КВК и их 2 или более слева и справа от dб, то точки кратные dб называют (Аi) аттракторами («притягивающими»). Для решающих интервалов между построенными точками их границы выбираются кратными одна меньшему делителю, другая – большему.

Для установления решающих интервалов и их границ выполняем детальный анализ окрестностей точек аттракторов (dб) (см.табл.1-15). При разметке числовой оси каждый аттрактор (Аi) как бы накрывается коротким интервалом (величиной из dm позиций, точек), совпадая с одной из промежуточных. Расстояние (в числе точек) аттрактора до ближайшей одной из границ накрывающего малого интервала всегда четное, до другой – нечетное.

Пример 2. Пусть задан составной модуль приведения N = dm·dб = 31·1129 = 34999 конечного числового кольца вычетов. Числовая ось (фрагмент ряда) разбита точками с шагами dm = 31 и dб = 1129. Требуется представить картину подобного разбиения фрагмента на отрезки и определить положение решающих ЗФБЧ интервалов с их характеристиками.

Решение. Начнем с первой (i = 1) точки (аттрактора А1) с координатой равной dб. Эта точка принадлежит замкнутому малому интервалу [31·36=1116, 1147 = 1116+31], накрывающему ее, 36dm 2 (mod 34999) = 81 = 9 2 и этот результат указывает на то, что этот интервал решающий, т. е. обеспечивает вычисление делителей модуля N. Вычисления делителей пока отложим.

Перейдем к рассмотрению интервала [1116, 1129] слева от А1 аттрактора, длина которого 13. Он не имеет целочисленной средней точки и не является решающим, но положение легко исправимо, переносом левой границы (Гл) в другую более близкую к началу координат (дальше от аттрактора) и кратную dм точку.

Исправленный новый интервал [Гл, Гп] = [1116 – 31, 1129] — решающий и он приобретает вид [1085, 1129] с изменившейся длиной 1129 – 1085 = 44, т. е. уже имеет среднюю точку, координата которой равна хц = ½ (Гл+ Гп) = ½ (1085 + 1129) = 1107.

Таким образом, найдены два (справа и слева) решающих ЗФБЧ интервала для аттрактора А1, т. е. точки 1·dб, ближайшей (i = 1) среди кратных к началу координат. Зададимся вопросом ограничено ли количество решающих интервалов для этого аттрактора? Если да, то чем определяется это ограничение?

Замечание. Квадратичные вычеты-дубли (за пределами области строк ТКВК), являющиеся полными квадратами – это всегда КВК центров решающих интервалов. Они являются дублями КВК из ТКВК. Их количество в ТКВК конечно и допустимое значение наибольшего из них ограничено.

В рассматриваемом примере порог maxКВК = r_лmax =√N=√34999=187,080, т. е. превышает 6-кратную длину малого интервала 6·31 = 186 187.

Следовательно, все значения КВК (дубли из ТКВК) могут принимать значения, не превышающие 187. Что касается количества решающих интервалов, группируемых аттракторами, то анализ ситуации показывает следующее.

Мощность множества ТКВК – это 187 элементов кольца, из которых не дублируются КВК кратных значений kmdm, km = 1(1)(187/ dm). В примере имеется шесть таких значений 31, 62, 93, 124, 157, 186. Строки СМ-модели в своем составе содержат строки, кратные разным делителям.

Строк кратных dб всего 15 = ½ (dm – 1), так в каждой из них сумма номера строки хо = dб и его дополнения х1 =N-dб остается постоянной равной N, т. е. дополнение х1 также кратно числу dб.

Из анализа нашего примера следует, что существует всего 15 аттракторов Аi, i = 1(1)15 и с каждым из них связаны по (186 – 6)/15 = 12 решающих интервалов, с центрами которых связаны дубли из ТКВК. Другими словами, сдвигаясь к началу координат с шагом 31, увеличиваем решающий интервал, КВВ в центре которого – получаем новый полный квадрат.

Пример 3. Используя данные примера А, вычислим решающие интервалы, наиболее удаленные влево и вправо от аттрактора А1. Левые интервалы:
[Гл, Гп] = [1116 – 62, 1129] = [1054, 1129] этот интервал не имеет целочисленной центральной точки хц = ½(Гл +Гп) = ½ (1054 + 1129) = 1091,5.
Обе границы интервалов должны быть нечетными числам кратными разным делителям.

Заметим, что положение центров (53 – 22 = 31) интервалов, как и их протяженности √(r_л) изменяются на величину кратную dм, а левой границы на 2dм. Таким образом, левые (правые) границы решающих интервалов и их центры принимают конкретные значения (здесь граница 1129 постоянная):

Зачеркнутые числа выходят за пределы допустимых элементов КЧКВ.

Для аттрактора А2 = 2dб и всех последующих вычисления аналогичные. Их результаты приведены далее в таблицах 1-15.

В работе здесь рассмотрена контурная модель НРЧ, связанная с изучением возможностей решения задачи факторизации больших чисел (ЗФБЧ). Особенность модели состоит в том, что в ней НРЧ представлен непрерывной последовательностью нумерованных (номер k = 1(1) ∞) контуров (блоков), размер которых (L(k)) с увеличением номера возрастает, но остается всегда кратным числу 8, L(k) = 8k.

Все контуры образованы двумя полуконтурами с размерами левый полуконтур m(k) = 4k –1 и правый контур – M(k) = 4k+1. Полуконтуры в k-м контуре имеют общую границу
Гц(k) = (2k) 2 – квадрат четного числа.

Длина (размер) каждого полуконтура – нечетное число и M(k)– m(k)= 2, а их сумма равна
M(k) + m(k) = L(k) длине k-го контура, левая и правая границы которого совпадают с левой границей меньшего и с правой – большего полуконтура.

Знак (+) соответствует левому полуконтуру и (–) – правому. Любое составное нечетное натуральное число (СННЧ) N >9, будем рассматривать как полуконтур или интервал в НРЧ с длиной N. Длина интервала – нечетное число равное сумме нечетного количества последовательных слагаемых (полуконтуров), в которой количество слагаемых равно меньшему делителю N, а среднее слагаемое – большему делителю N.

В действительности нам известны лишь N и, что оно составное, равно произведению двух простых чисел.

Рассматриваются составные нечетные натуральные числа (СННЧ) среди которых нет чисел N =k 2 полных нечетных квадратов.

Дело в том, что такие квадраты дают другую картину распределения квадратичных вычетов (КВВ) элементов кольца, отличающуюся от картины для полупростых чисел N = pq, p 2 из тривиальной области не дублируются в списочной многострочной модели (СММ) числа и закон распределения делителей (ЗРД) в такой ситуации не работает.

Напомним, что в СММ при дублировании одного из вычетов строки дублируются и другие два. При этом, если делители p и q не очень близки (далеки) друг от друга, то в области тривиальных строк ТКВК имеются две строки, содержащие средние вычеты со свойством, сохранять смежность сомножителей (ССС).

Утверждение. Для двух нечетных произвольных простых чисел p и q их сумма ∑ и разность Δ четные и либо их сумма ∑ = (р + q), либо их разность Δ = (р – q) делится на 4.

Расстояние (в числе строк) между этими строками равно меньшему делителю р. Номер верхней строки с дублируемым средним вычетом определяется соотношением хов = (р – q):4. Отсюда номер нижней строки равен хон = хов + р. Положение этих (верхняя и нижняя) строк определяются элементами колонки Тп, которые кратны меньшему делителю.

В случае, когда разность делителей Δ = (р – q) не делится на 4, а сумма делится, то номер верхней строки равен хов = хон – ½ Δ, где хон = (р + q):4.

В области строк СММ тривиальных средних вычетов, также появляются две строки, содержащие средние вычеты и дублируемые левые КВВ, с теми же значениями вычетов, что и в верхней части модели.

Области аттракции модуля сравнения N = 34999 конечного числового кольца

Размах области аттракции постоянный для всех аттракторов (равен 341 строке), кроме той, что содержит инволюцию (увеличен на dm =31 строку).

Между областями аттракции интервалы либо 766, либо 797 строк. Области хорошо разделены, хотя их влияние друг на друга не исключается.

Сближение значений делителей изменяет (уменьшает) удаленность областей вплоть до того, что области «наезжают» одна на другую и разобраться с решающими интервалами становится проблематично. Но закон распределения делителей (ЗРД) числа работает и в этих условиях. Здесь возникает множество вопросов, ответы на которые пока не получены.