квантово химическое описание элементарного акта химической реакции

КВАНТОВО-ХИМИЧЕСКОЕ ОПИСАНИЕ РЕАКЦИЙ

Химические реакции в газовой фазе 5

Элементарный акт химической реакции 9

Теория переходного состояния химической реакции 13

Расчет поверхности потенциальной энергии химической реакции 15

Расчет особых точек ППЭ 19

Путь химической реакции 24

Полуколичественная оценка геометрии переходного состояния

химической реакции 28

Квантово-химическое описание реакций в жидкой и твердой фазе 30

Роль орбитальной симметрии 32

Индексы реакционной способности 36

Молекулярный электростатический потенциал 38

Метод граничных орбиталей. Теория жестких и мягких кислот и

Абсолютная жесткость и абсолютная мягкость молекулярных систем 48

Валентность атома и порядок связи 55

Энергия диссоциации химической связи в молекулярной системе 56

Орбитальные модели взаимодействия молекул с поверхностью.

Квантовая химия каталитических реакций 59

Затратив достаточное количество усилий, всегда можно

из бесконечного множества теорий выбрать

удовлетворяющие конечному множеству экспериментов.

В методах термохимии и кинетики химическая реакция изучается измерением макроскопических свойств атомно-молекулярных ансамблей. Современная экспериментальная техника позволяет исследовать химический процесс на уровне элементарного акта. Но таким образом исследован узкий круг реакций. Обычно механизм химической реакции, причины различий реакционной способности реагентов получают лишь косвенные обоснования.

Квантовая химия позволяет понять механизмы химических реакций, смоделировать синтез новых молекул с заданными свойствами (молекулярный дизайн). Расчет дает поверхность потенциальной энергии; с особыми точками этой поверхности связаны равновесные и переходные состояния системы в совокупности элементарных актов химической реакции. Анализ особых точек приводит к характеристикам, непосредственно связанным с макроскопическими свойствами молекул. Учет свойств переходного состояния химической реакции и теория возмущений позволяют трактовать результаты квантово-химического расчета и с помощью различных индексов предсказывать реакционную способность молекул.

Авторы благодарны профессору А.В. Тулубу кафедры квантовой химии химического факультета Санкт-Петербургского университета (СПбГУ) за конструктивные замечания и плодотворное обсуждение пособия.

Химические реакции в газовой фазе

Квантовая химия по сравнению с кинетикой и термохимией открывает новые возможности для изучения химических реакций, позволяя расчетным путем проследить ненаблюдаемое экспериментально движение реагирующей системы между реагентами и продуктами. Однако как всякое теоретическое рассмотрение она нуждается в экспериментальном подтверждении. Рассмотрим, какие величины и как следует рассчитывать, чтобы описать химические реакции и корректно сравнить результаты теоретических расчетов с экспериментом.

Ответ на первую часть вопроса дают статистическая термодинамика и теория химической кинетики. В их основе лежат представления Аррениуса, развитые в теории абсолютных скоростей химических реакций (они подробно рассматриваются в курсе «Физическая химия»):

поверхность потенциальной энергии (ППЭ) как вещественный образ химической реакции;

минимумы ППЭ в долинах реагентов и продуктов реакции, соответствующие равновесным состояниям;

переходное состояние или активированный комплекс – точка максимума ППЭ;

путь химической реакции – классическая траектория поступательного движения изображающей точки из долины реагентов в долину продуктов через точку переходного состояния.

Успех теоретических расчетов скоростей химических реакций доказал плодотворность этих понятий.

Квантовая теория выявила физический смысл вышеперечисленных интуитивных представлений и дала им строгие определения. Это позволило разработать методы их расчета и ответить на вопрос как следует рассчитывать величины, описывающие химические реакции.

Схема сравнения результатов квантово-химических расчетов с данными измерений по методам термохимии и кинетики для реакций между молекулами идеальных газов представлена рис. 1 [1]. Прежде всего принимают приближение Борна-Оппенгеймера, в результате чего уравнение Шредингера для электронно-ядерной системы распадается на уравнение Шредингера для электронов и уравнение Шредингера для ядер. Колебательную задачу, состоящую в решении уравнения Шредингера для ядер, мы опускаем из рассмотрения. Совокупность решений уравнения Шредингера для электронов при различных конфигурациях ядерной подсистемы определяет поверхность потенциальной энергии (ППЭ) химической реакции как совокупность точек, характеризуемых определенной энергией системы при фиксированном положении ядер. Решение электронного уравнения Шредингера по методу молекулярных орбиталей было рассмотрено в разделе «Квантовая химия молекулы» курса «Введение в квантовую химию». Для понимания последующего материала достаточно помнить, что в результате получаются потенциальная энергия основного состояния реагирующей системы и электронная волновая функция. Мы опускаем из рассмотрения все случаи, когда приближение Борна-Оппенгеймера несправедливо и взаимодействием электронной и ядерной подсистем пренебречь нельзя (другими словами, мы, в частности, не касаемся свойств, обусловленных эффектом Яна-Теллера). Ограничимся рассмотрением ППЭ основного электронного состояния реагирующей системы.

Размерность пространства, в котором определяется ППЭ, для N взаимодействующих частиц задается числом координат, принятых в качестве степеней свободы (3N – 6 для нелинейных и 3N – 5 для линейных систем, соответственно) плюс 1 (энергия): 3N – 5 (3N – 4). Из всех этих координат

Уравнение Шредингера для электронов и ядер

Уравнение Шредингера для электронов. Уравнения Хартри-Фока

Уравнение Шредингера для ядер

Теория молекулярных орбиталей

Поверхность потенциальной энергии основного состояния реагирующей системы. Энергетические профили и двумерные сечения

Геометрия и энергия равновесного состояния реагирующей системы

Геометрия и энергия переходного состояния реагирующей системы

Разделение колебаний и вращений

Вращательные энергетические уровни реагирующей системы

Колебательные энергетические уровни реагирующей системы

Трансляционная функция распределения реагирующей системы

Вращательная функция распределения реагирующей системы

Колебательная функция распределения реагирующей системы

Энергия нулевых колебаний реагирующей системы

Энтальпия, энтропия, теплоемкость.

Энтальпия активации, энтропия активации.

Методы термохимии Методы кинетики

Рис. 1. Приближенная схема вычисления термодинамических и кинетических параметров реагирующих молекул идеальных газов по их молекулярным свойствам. Жирным шрифтом выделены промежуточные результаты вычислений, курсивом – приближения или (и) методы их получения

может быть выделена одна, непрерывно соединяющая долину исходных веществ и долину продуктов через точку локального максимума – переходное состояние или активированный комплекс. Эта координата называется координатой реакции.

Для количественного описания реакций интерес представляют одно- и

Рис. 2. Энергетический профиль ППЭ вдоль координаты реакции электрофильного замещения в ароматическом кольце. Цифрами обозначены четыре стадии реакции

Элементарный акт химической реакции.

В квантовой химии каждую стадию реакции принято рассматривать как элементарный акт (единичный акт превращения реагентов в продукты). Пример такого рассмотрения для элементарного акта некоторой многостадийной реакции представлен рис. 3. Сечение (профиль) ППЭ вдоль координаты реакции для элементарного акта (в общем случае) содержит 5 особых точек:

1. Бесконечно удаленные реагенты.

2. Предреакционный комплекс – ван-дер-ваальсов или со специфическими

Рис. 3. Энергетический профиль ППЭ вдоль координаты реакции для элементарного акта некоторой многостадийной реакции

3. Переходное состояние.

4. Послереакционный комплекс – ван-дер-ваальсов или со специфическими взаимодействиями.

5. Бесконечно удаленные продукты.

Отметим, что на больших расстояниях взаимодействие между частицами реагентов или продуктов может быть описано и достаточно простыми потенциалами без анализа всех деталей строения ППЭ [2].

Характеристиками реакционной способности системы являются разности энергий перечисленных особых точек, относящиеся к Т = 0 К. Рассмотрим два основных вида реакций, состоящих в преобразовании : 1) предреакционного комплекса АВ в послереакционный комплекс CD; 2) реагентов А + В в продукты C + D.

1) Для реакции AB  CD :

Энергия активации Е_а 0 или Е*– разность полных энергий переходного состояния АВ * (3) и предреакционного комплекса АВ (2).

Тепловой эффект химической реакции Н 0 или Н – разность полных энергий после- и предреакционного комплексов CD (4) и АВ (2).

2) Для реакции A + B  C + D :

Энергия активации Е_а или Е – разность полных энергий переходного состояния АВ * (3) и свободных реагентов А + В (1).

Тепловой эффект химической реакции Н_р или Н_р * – разность полных энергий продуктов C + D (5) и реагентов А + В (1).

Заметим, что рассмотрение межмолекулярных взаимодействий, важнейшее, в частности, в биохимических процессах, основано на изучении реакций вида А + В  АВ. При этом рассчитывается разность полных энергий комплекса АВ (2) и свободных реагентов А + В (1).

Преобразование энергии активации Е_а 0 в Е*, Е_а в Е и теплового эффекта Н 0 в Н, Н_р в Н_р * может быть осуществлено с помощью энергии нулевых колебаний Е_нк исследуемых систем (см. ниже). Е_нк – разность энергий низшего колебательного состояния гармонического осциллятора (при значении полного колебательного квантового числа, равном нулю) и минимума ППЭ, соответствующего изучаемому состоянию системы.

В качестве примера рассмотрим результаты квантово-химического расчета первой стадии реакции радикального окисления метана, весьма важной с технологической точки зрения:

Легко видеть, что по абсолютной величине энергия активации Е (Е_а) много меньше полных энергий реагентов и переходного состояния, с которыми она вычисляется. Поэтому использование расширенного базиса и учет корреляционной энергии весьма желательны (смотри раздел «Квантовая химия молекул» курса «Введение в квантовую химию») для повышения точности расчета. Параметры Е (Е_а), Е* (Е_а 0 ), Н (Н 0 ), Н_р * (Н_р) обычно применяют для расчета термодинамических и кинетических параметров, которые в рамках теории переходного состояния могут сравниваться с экспериментальными величинами.

Источник

Теория элементарного акта химической реакции

Все рассмотренные выше кинетические уравнения направлены на определение констант скорости по экспериментальным данным С(τ) или х(τ). В свою очередь, константа скорости представляет собой основную величину, необходимую для проведения любых кинетических и технологических расчетов. Мы видели, что экспериментальное определения констант является достаточно трудоемкой задачей, даже в случае относительно простых реакций. Возникает вопрос, нельзя ли рассчитать константу скорости реакции, исходя из теоретических представлений, как это сделано в термодинамике для констант равновесия? С этой целью для расчета константы скорости реакции 2го порядка в теоретической кинетике были предложены 2 подхода:

1) теория активных соударений и

2) теория переходного состояния (абс. скор. реакции).

3.1 Теория активных соударений

Начнем с более простой теории активных соударений (АС), разработанной Аррениусом и Хиншельвудом в развитие 1-го и 2-го постулатов кинетики. В теории АС реагирующие частицы упрощенно считаются упругими шарами. Поскольку для протекания реакции необходимо столкновение 2 частиц (1й постулат), суммарная энергия которых ≥ Е (2й постулат), для расчета скорости реакции необходимо рассчитать число столкновений (z) в единицу времени, в единице реакционного пространства и найти долю активных соударений (ε). Произведение zε будет представлять собой расчетную скорость реакции. Активными считаются соударения, в которых система частиц имеет энергию Е≥Е_a.

В качестве реакционного пространства выберем т. н. цилиндр соударений с диаметром (δ_AB), равным полусумме диаметров молекул А и В, и высотой, равной длине свободного пробега (l₀) между двумя столкновениями. Очевидно, что l₀ равна произведению средней скорости движения молекул (ω) на время между двумя столкновениями Δt.

А

Рис. 13. Цилиндр соударений молекул A и B

Выразим скорость движения молекул согласно кинетической теории газов

где μ = (Ма + Мв)/Ма•Мв – функция молекулярных масс реагентов. Тогда число столкновений молекул А и В в единицу времени Δt, в единичном цилиндре определяется выражением:

Доля активных соударений определяется функцией распределения молекул по энергии Максвелла-Больцмана, согласно которой

ε == exp(-E/RT) (3.3)

Заметим, что доля активных соударений растет с температурой существенно быстрее, чем кинетическая энергия частиц. Например, при увеличении температуры от 1000 до 2000К средняя кинетическая энергия частиц увеличивается в 2 раза, а доля молекул с энергией

Е≥ 80 кДж/моль возрастает приблизительно в 150 раз.

Таким образом, перемножая уравнения 2 и 3, получим расчетное выражение скорости реакции по теории АС:

При сопоставлении (3.4) с уравнением кинетики r = kC_AC_B видно, что величина константы скорости по теории АС имеет вид:

Теория АС позволяет рассчитать только величину k, а энергию активации Е определяют экспериментально. Из уравнения 3.5 видно, что предэкспоненциальный множитель слабо зависит от температуры (как Т 1/2 ). Поэтому экспериментально наблюдаемая величина Е_н, найденная по уравнению Аррениуса, будет отличаться от истинной Е на величину, которую можно найти из (3.5) после логарифмирования:

и дифференцирования этого выражения:

Следовательно, найденная Е_н будет отличаться от истинной Е_а на ½ RT. Ввиду малости этой поправки (она составляет 1-1,5 кДж/моль в интервале 300-400К и 4,2 при 1000К) величиной (½ RT) обычно пренебрегают.

Посмотрим теперь, насколько хорошо «работает» теория активных соударений. С этой целью сопоставим экспериментальные и расчетные значения предэкспоненциального множителя для некоторых газофазных реакций, приведенные в табл. 3.

Таблица 3. Параметры Аррениуса для газофазных бимолекулярных реакций

Как видно из табл. 3 теория АС для реакций 1, 4, 5 дает качественное соответствие предэкспоненциального множителя в пределах порядка величины, а для реакций 2 и 3 результативными являются лишь 0,008 и 1,7 из миллиона соударений. Следовательно, кроме энергии столкновения, имеется неучтенный фактор протекания реакции. Этот стерический фактор, учитывает вероятность благоприятной конфигурации частиц при соударении. Было установлено, что, например, для протекания реакции 2 необходимо, чтобы ось молекулы водорода Н-Н при соударении была перпендикулярна плоскости метильного радикала, а для реакции 3 необходимо, чтобы оси молекул С₂Н₄ и Н₂ были параллельны (для максимального перекрывания s–орбитали водорода c π–орбиталью этилена).

Таким образом, согласно уточненной теории АС скорость реакции определяется тремя факторами: стерическим (f), энергетическим (ε) и транспортным (Z) или

причем 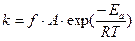(3.9)

Транспортный фактор Z определяет частоту соударений молекул реагентов, энергетический фактор ε учитывает долю молекул с энергией, необходимой для реакций, а стерический фактор учитывает долю молекул с надлежащей конфигурацией при соударении.

Следовательно, теория активных соударений дает качественную оценку предэкспоненциального множителя только для сферически симметричных молекул. Очевидная недостаточность теории АС стимулировала поиск более перспективных моделей расчета скорости химических реакций. Такая модель активированного комплекса была положена в основу теории абсолютных скоростей химических реакцийили:

3.2 Теория переходного состояния

Теория переходного состояния (ПС) была разработана Эйрингом и Поляни (1935) с использованием аппарата статистической термодинамики. В модели активированного комплекса (АК) или переходного состояния предполагается, что исходная конфигурация реагирующих частиц, обладающих достаточной энергией для преодоления барьера реакции, преобразуется при непрерывном изменении межатомных расстояний и соответствующей энергии системы в активированный комплекс, который обязательно превращается в продукты реакции. Например, для реакции

для превращения исходных молекул АА и В в продукты они обязательно должны образовать некий активированный комплекс ААВ (рис. 15).

Е δ ▲ АА+В АВА ■ ●	Рис. 15. Изменение потенциальной энергии в ходе превращения исходных веществ АА и В в продукт ABA через активированный комплекс
Координата реакции, ρ

В переходном комплексе старые связи существенно искажены (разрыхлены), и наметились уже новые связи, однако их конфигурация и соответствующая энергия не соответствуют стабильным молекулам.

Задачи по кинетике

1. Энергия активации гидрирования ацетилена равна 40 кДж/моль. Кинетическое уравнение имеет вид:

r= k (P_С2Н2) 0,5 (P_Н2 ) 0,5 ; скорость реакции при 300 К и Р(Н₂)= Рац = 0,5 атм равна 1 моль/(л.с). Найти r в условиях.: вар.1) Т = 350К Рэ = 1 и Р_Н2= 2 атм

2. Константа скорости реакции второго порядка Н₂ + Cl₂ = 2НСl:

k= 0,2 л/(моль.c), [H₂]= 15 ммоль/л. Найти время, обеспечивающее данную степень превращения хлора (х= 75%), и количество катализатора, дающего производительность по НСl (П= 1,5 куб. м/мин); соотношение Н₂ /Cl₂ = 3 (моли).

3. Энергия активации распада оксида этилена равна 210 кДж/моль; время полураспада оксида: t ½ = 150 мин при 650К. Найти константу скорости реакции (1й порядок) при температуре 750К

5. Энергия активации гидрирования этилена равна 45 кДж/моль, а порядок реакции по С₂Н₄ и Н₂ равен 1 и 1,5; скорость реакции при 300 К и Р(Н₂)= Рэ = 1 атм равна 1 моль/(л.с). Найти скорость реакции при: Т = 350К Рэ = 2 и Р(Н₂)= 2,5 атм

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

КВАНТОВО-ХИМИЧЕСКОЕ ОПИСАНИЕ РЕАКЦИЙ

Химические реакции в газовой фазе 5

Элементарный акт химической реакции 9

Теория переходного состояния химической реакции 13

Расчет поверхности потенциальной энергии химической реакции 15

Расчет особых точек ППЭ 19

Путь химической реакции 24

Полуколичественная оценка геометрии переходного состояния

химической реакции 28

Квантово-химическое описание реакций в жидкой и твердой фазе 30

Роль орбитальной симметрии 32

Индексы реакционной способности 36

Молекулярный электростатический потенциал 38

Метод граничных орбиталей. Теория жестких и мягких кислот и

Абсолютная жесткость и абсолютная мягкость молекулярных систем 48

Валентность атома и порядок связи 55

Энергия диссоциации химической связи в молекулярной системе 56

Орбитальные модели взаимодействия молекул с поверхностью.

Квантовая химия каталитических реакций 59

Затратив достаточное количество усилий, всегда можно

из бесконечного множества теорий выбрать

удовлетворяющие конечному множеству экспериментов.

В методах термохимии и кинетики химическая реакция изучается измерением макроскопических свойств атомно-молекулярных ансамблей. Современная экспериментальная техника позволяет исследовать химический процесс на уровне элементарного акта. Но таким образом исследован узкий круг реакций. Обычно механизм химической реакции, причины различий реакционной способности реагентов получают лишь косвенные обоснования.

Квантовая химия позволяет понять механизмы химических реакций, смоделировать синтез новых молекул с заданными свойствами (молекулярный дизайн). Расчет дает поверхность потенциальной энергии; с особыми точками этой поверхности связаны равновесные и переходные состояния системы в совокупности элементарных актов химической реакции. Анализ особых точек приводит к характеристикам, непосредственно связанным с макроскопическими свойствами молекул. Учет свойств переходного состояния химической реакции и теория возмущений позволяют трактовать результаты квантово-химического расчета и с помощью различных индексов предсказывать реакционную способность молекул.

Авторы благодарны профессору А.В. Тулубу кафедры квантовой химии химического факультета Санкт-Петербургского университета (СПбГУ) за конструктивные замечания и плодотворное обсуждение пособия.

Химические реакции в газовой фазе

Квантовая химия по сравнению с кинетикой и термохимией открывает новые возможности для изучения химических реакций, позволяя расчетным путем проследить ненаблюдаемое экспериментально движение реагирующей системы между реагентами и продуктами. Однако как всякое теоретическое рассмотрение она нуждается в экспериментальном подтверждении. Рассмотрим, какие величины и как следует рассчитывать, чтобы описать химические реакции и корректно сравнить результаты теоретических расчетов с экспериментом.

Ответ на первую часть вопроса дают статистическая термодинамика и теория химической кинетики. В их основе лежат представления Аррениуса, развитые в теории абсолютных скоростей химических реакций (они подробно рассматриваются в курсе «Физическая химия»):

поверхность потенциальной энергии (ППЭ) как вещественный образ химической реакции;

минимумы ППЭ в долинах реагентов и продуктов реакции, соответствующие равновесным состояниям;

переходное состояние или активированный комплекс – точка максимума ППЭ;

путь химической реакции – классическая траектория поступательного движения изображающей точки из долины реагентов в долину продуктов через точку переходного состояния.

Успех теоретических расчетов скоростей химических реакций доказал плодотворность этих понятий.

Квантовая теория выявила физический смысл вышеперечисленных интуитивных представлений и дала им строгие определения. Это позволило разработать методы их расчета и ответить на вопрос как следует рассчитывать величины, описывающие химические реакции.

Схема сравнения результатов квантово-химических расчетов с данными измерений по методам термохимии и кинетики для реакций между молекулами идеальных газов представлена рис. 1 [1]. Прежде всего принимают приближение Борна-Оппенгеймера, в результате чего уравнение Шредингера для электронно-ядерной системы распадается на уравнение Шредингера для электронов и уравнение Шредингера для ядер. Колебательную задачу, состоящую в решении уравнения Шредингера для ядер, мы опускаем из рассмотрения. Совокупность решений уравнения Шредингера для электронов при различных конфигурациях ядерной подсистемы определяет поверхность потенциальной энергии (ППЭ) химической реакции как совокупность точек, характеризуемых определенной энергией системы при фиксированном положении ядер. Решение электронного уравнения Шредингера по методу молекулярных орбиталей было рассмотрено в разделе «Квантовая химия молекулы» курса «Введение в квантовую химию». Для понимания последующего материала достаточно помнить, что в результате получаются потенциальная энергия основного состояния реагирующей системы и электронная волновая функция. Мы опускаем из рассмотрения все случаи, когда приближение Борна-Оппенгеймера несправедливо и взаимодействием электронной и ядерной подсистем пренебречь нельзя (другими словами, мы, в частности, не касаемся свойств, обусловленных эффектом Яна-Теллера). Ограничимся рассмотрением ППЭ основного электронного состояния реагирующей системы.

Размерность пространства, в котором определяется ППЭ, для N взаимодействующих частиц задается числом координат, принятых в качестве степеней свободы (3N – 6 для нелинейных и 3N – 5 для линейных систем, соответственно) плюс 1 (энергия): 3N – 5 (3N – 4). Из всех этих координат

Уравнение Шредингера для электронов и ядер

Уравнение Шредингера для электронов. Уравнения Хартри-Фока

Уравнение Шредингера для ядер

Теория молекулярных орбиталей

Поверхность потенциальной энергии основного состояния реагирующей системы. Энергетические профили и двумерные сечения

Геометрия и энергия равновесного состояния реагирующей системы

Геометрия и энергия переходного состояния реагирующей системы

Разделение колебаний и вращений

Вращательные энергетические уровни реагирующей системы

Колебательные энергетические уровни реагирующей системы

Трансляционная функция распределения реагирующей системы

Вращательная функция распределения реагирующей системы

Колебательная функция распределения реагирующей системы

Энергия нулевых колебаний реагирующей системы

Энтальпия, энтропия, теплоемкость.

Энтальпия активации, энтропия активации.

Методы термохимии Методы кинетики

Рис. 1. Приближенная схема вычисления термодинамических и кинетических параметров реагирующих молекул идеальных газов по их молекулярным свойствам. Жирным шрифтом выделены промежуточные результаты вычислений, курсивом – приближения или (и) методы их получения

может быть выделена одна, непрерывно соединяющая долину исходных веществ и долину продуктов через точку локального максимума – переходное состояние или активированный комплекс. Эта координата называется координатой реакции.

Для количественного описания реакций интерес представляют одно- и

Рис. 2. Энергетический профиль ППЭ вдоль координаты реакции электрофильного замещения в ароматическом кольце. Цифрами обозначены четыре стадии реакции

Элементарный акт химической реакции.

В квантовой химии каждую стадию реакции принято рассматривать как элементарный акт (единичный акт превращения реагентов в продукты). Пример такого рассмотрения для элементарного акта некоторой многостадийной реакции представлен рис. 3. Сечение (профиль) ППЭ вдоль координаты реакции для элементарного акта (в общем случае) содержит 5 особых точек:

1. Бесконечно удаленные реагенты.

2. Предреакционный комплекс – ван-дер-ваальсов или со специфическими

Рис. 3. Энергетический профиль ППЭ вдоль координаты реакции для элементарного акта некоторой многостадийной реакции

3. Переходное состояние.

4. Послереакционный комплекс – ван-дер-ваальсов или со специфическими взаимодействиями.

5. Бесконечно удаленные продукты.

Отметим, что на больших расстояниях взаимодействие между частицами реагентов или продуктов может быть описано и достаточно простыми потенциалами без анализа всех деталей строения ППЭ [2].

Характеристиками реакционной способности системы являются разности энергий перечисленных особых точек, относящиеся к Т = 0 К. Рассмотрим два основных вида реакций, состоящих в преобразовании : 1) предреакционного комплекса АВ в послереакционный комплекс CD; 2) реагентов А + В в продукты C + D.

1) Для реакции AB  CD :

Энергия активации Е_а 0 или Е*– разность полных энергий переходного состояния АВ * (3) и предреакционного комплекса АВ (2).

Тепловой эффект химической реакции Н 0 или Н – разность полных энергий после- и предреакционного комплексов CD (4) и АВ (2).

2) Для реакции A + B  C + D :

Энергия активации Е_а или Е – разность полных энергий переходного состояния АВ * (3) и свободных реагентов А + В (1).

Тепловой эффект химической реакции Н_р или Н_р * – разность полных энергий продуктов C + D (5) и реагентов А + В (1).

Заметим, что рассмотрение межмолекулярных взаимодействий, важнейшее, в частности, в биохимических процессах, основано на изучении реакций вида А + В  АВ. При этом рассчитывается разность полных энергий комплекса АВ (2) и свободных реагентов А + В (1).

Преобразование энергии активации Е_а 0 в Е*, Е_а в Е и теплового эффекта Н 0 в Н, Н_р в Н_р * может быть осуществлено с помощью энергии нулевых колебаний Е_нк исследуемых систем (см. ниже). Е_нк – разность энергий низшего колебательного состояния гармонического осциллятора (при значении полного колебательного квантового числа, равном нулю) и минимума ППЭ, соответствующего изучаемому состоянию системы.

В качестве примера рассмотрим результаты квантово-химического расчета первой стадии реакции радикального окисления метана, весьма важной с технологической точки зрения:

Легко видеть, что по абсолютной величине энергия активации Е (Е_а) много меньше полных энергий реагентов и переходного состояния, с которыми она вычисляется. Поэтому использование расширенного базиса и учет корреляционной энергии весьма желательны (смотри раздел «Квантовая химия молекул» курса «Введение в квантовую химию») для повышения точности расчета. Параметры Е (Е_а), Е* (Е_а 0 ), Н (Н 0 ), Н_р * (Н_р) обычно применяют для расчета термодинамических и кинетических параметров, которые в рамках теории переходного состояния могут сравниваться с экспериментальными величинами.

Источник