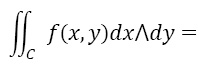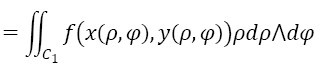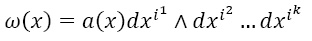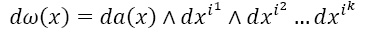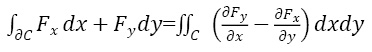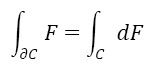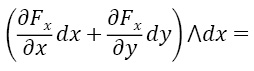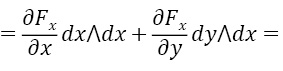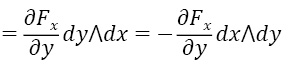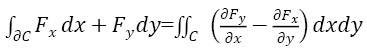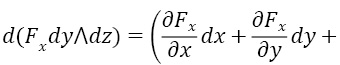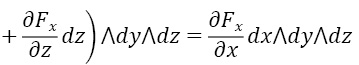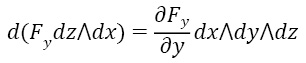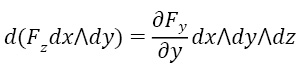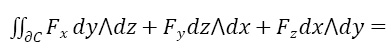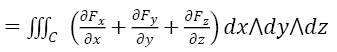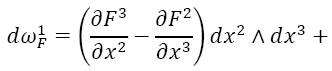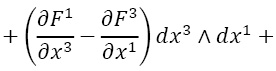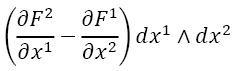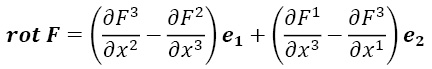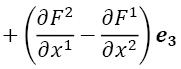зачем нужны дифференциальные формы
в математический поля дифференциальная геометрия и тензорное исчисление, дифференциальные формы подход к многомерное исчисление это не зависит от координаты. Дифференциальные формы обеспечивают единый подход к определению интегрирует над кривыми, поверхностями, телами и многомерными коллекторы. Современное понятие дифференциальных форм было впервые предложено Эли Картан. Он имеет множество приложений, особенно в геометрии, топологии и физике.
Содержание
История
Дифференциальные формы являются частью области дифференциальной геометрии, на которую влияет линейная алгебра. Хотя понятие дифференциала довольно старое, первоначальную попытку алгебраической организации дифференциальных форм обычно приписывают Эли Картан со ссылкой на его статью 1899 года. [1] Некоторые аспекты внешняя алгебра дифференциальных форм появляется в Герман Грассманнработа 1844 г., Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik (Теория линейного расширения, новый раздел математики).
Концепция
Дифференциальные формы обеспечивают подход к многомерное исчисление это не зависит от координаты.
Интеграция и ориентация
которая является отрицательной величиной интеграла той же дифференциальной формы на том же интервале, когда используется противоположная ориентация. То есть:
Это дает геометрический контекст условности для одномерных интегралов знак меняется при изменении ориентации интервала на противоположную. Стандартное объяснение этого в теории интегрирования с одной переменной состоит в том, что когда пределы интегрирования находятся в противоположном порядке ( б ), приращение dx отрицательно в направлении интеграции.
Мультииндексная нотация
Внешняя производная
Сама внешняя производная применяется в произвольном конечном числе измерений и представляет собой гибкий и мощный инструмент с широким применением в дифференциальная геометрия, дифференциальная топология, и многие области физики. Следует отметить, что хотя приведенное выше определение внешней производной было определено относительно локальных координат, ее можно определить совершенно бескординатным способом, как антидеривация степени 1 на внешняя алгебра дифференциальных форм. Преимущество этого более общего подхода состоит в том, что он позволяет использовать естественный бескординатный подход к интегрированию на коллекторы. Это также позволяет естественным образом обобщить основная теорема исчисления, называемый (обобщенным) Теорема Стокса, что является центральным результатом теории интегрирования на многообразиях.
Дифференциальное исчисление
(Это понятие можно распространить точечно на случай, когда v это векторное поле на U оценивая v в момент п в определении.)
Первой идеей, ведущей к дифференциальным формам, является наблюдение, что ∂v ж (п) это линейная функция из v :
Смысл этого выражения дается путем оценки обеих сторон в произвольной точке п : в правой части указана сумма «точечно», так что
так что найти такой ж пока не
куда ∧ определяется так, что:
Внутренние определения
По универсальному свойству внешних степеней это эквивалентно чередование многолинейная карта:
Внешняя алгебра может быть вложена в тензорную алгебру с помощью отображения чередования. Карта чередования определяется как отображение
куда Sk это симметричная группа на k элементы. Отображение альтернирования постоянно на смежных классах идеала в тензорной алгебре, порожденной симметричными 2-формами, и поэтому спускается до вложения
Операции
Помимо сложения и умножения с помощью скалярных операций, которые возникают из структуры векторного пространства, существует несколько других стандартных операций, определенных для дифференциальных форм. Наиболее важными операциями являются внешний продукт двух дифференциальных форм внешняя производная единой дифференциальной формы интерьерный продукт дифференциальной формы и векторного поля Производная Ли дифференциальной формы относительно векторного поля и ковариантная производная дифференциальной формы относительно векторного поля на многообразии с определенной связностью.
Внешний продукт
Антисимметрия, присущая внешней алгебре, означает, что когда α ∧ β рассматривается как полилинейный функционал, он знакопеременный. Однако, когда внешняя алгебра вложила подпространство тензорной алгебры с помощью отображения альтернирования, тензорное произведение α ⊗ β не чередуется. Существует явная формула, описывающая внешний вид продукта в этой ситуации. Внешний вид продукта
Риманово многообразие
Структуры векторных полей
Внешний дифференциальный комплекс
Откат
Pullback учитывает все основные операции с формами. Если ω и η формы и c это действительное число, тогда
Интеграция
Интеграция в евклидовом пространстве
Интеграция по цепочкам
Предположим, что φ определяется
Тогда интеграл в координатах можно записать как
является определителем Якобиан. Якобиан существует потому, что φ дифференцируема.
Интеграция с использованием разделов единства
Интеграция по волокнам
Обозначим эту форму через
Потом (Дьедон, 1972) ошибка harv: цель отсутствует: CITEREFDieudonne1972 (помощь) доказывает обобщенную формулу Фубини
определяется предметом интерьера
Теорема Стокса
Эта теорема также лежит в основе двойственности между когомологии де Рама и гомология цепей.
Связь с мерами
Течения
Приложения в физике
Дифференциальные формы возникают в некоторых важных физических контекстах. Например, в теории Максвелла электромагнетизм, то 2-форма Фарадея, или же напряженность электромагнитного поля, является
Используя приведенные выше определения, Уравнения Максвелла можно очень компактно записать на геометрические единицы в качестве
Приложения в геометрической теории меры
Многочисленные результаты о минимальности для комплексных аналитических многообразий основаны на Неравенство Виртингера для 2-форм. Краткое доказательство можно найти в Герберт Федерерклассический текст Геометрическая теория меры. Неравенство Виртингера также является ключевым элементом Неравенство Громова для комплексного проективного пространства в систолическая геометрия.
СОДЕРЖАНИЕ
История
Концепция
Интеграция и ориентация
которая является отрицательной величиной интеграла той же дифференциальной формы на том же интервале, когда используется противоположная ориентация. То есть:
Это придает геометрический контекст соглашениям об одномерных интегралах, согласно которым знак меняется при изменении ориентации интервала на противоположную. Стандартное объяснение этого в теории интегрирования одной переменной состоит в том, что, когда пределы интегрирования находятся в противоположном порядке ( b ), приращение dx отрицательно в направлении интегрирования.
Мультииндексная нотация
Внешняя производная
Дифференциальное исчисление
Первой идеей, ведущей к дифференциальным формам, является наблюдение, что ∂ v f ( p ) является линейной функцией от v :
Смысл этого выражения дается путем вычисления обеих сторон в произвольной точке p : в правой части сумма определяется « поточечно », так что
поэтому найти такое f будет невозможно, если только
где ∧ определяется так, что:
Внутренние определения
По универсальному свойству внешних степеней это эквивалентно чередующемуся полилинейному отображению :
Внешняя алгебра может быть вложена в тензорную алгебру с помощью отображения чередования. Карта чередования определяется как отображение
Операции
Помимо сложения и умножения с помощью скалярных операций, которые возникают из структуры векторного пространства, существует несколько других стандартных операций, определенных для дифференциальных форм. Наиболее важными операциями являются внешнее произведение двух дифференциальных форм, внешняя производная одной дифференциальной формы, внутреннее произведение дифференциальной формы и векторного поля, производная Ли дифференциальной формы относительно векторного поля и ковариантная производная дифференциальной формы по векторному полю на многообразии с заданной связностью.
Внешний продукт
Антисимметрия, присущая внешней алгебре, означает, что когда α ∧ β рассматривается как полилинейный функционал, он является альтернированным. Однако, когда внешняя алгебра вложила подпространство тензорной алгебры с помощью отображения альтернирования, тензорное произведение α ⊗ β не является альтернированным. Существует явная формула, описывающая внешний вид продукта в этой ситуации. Внешний вид продукта
Риманово многообразие
Структуры векторных полей
Внешний дифференциальный комплекс
Откат
Интеграция
Интеграция в евклидовом пространстве
Интеграция по цепочкам
Предположим, что φ определяется формулой
Тогда интеграл в координатах можно записать как
Интеграция с использованием разделов единства
Интеграция по волокнам
Обозначим эту форму через
Затем ( Dieudonne 1972 ) доказывает обобщенную формулу Фубини ошибка harv: цель отсутствует: CITEREFDieudonne1972 ( справка )
определяется предметом интерьера
Теорема Стокса
Эта теорема также лежит в основе двойственности между когомологиями де Рама и гомологиями цепей.
Связь с мерами
Течения
Приложения в физике
Используя упомянутые выше определения, уравнения Максвелла могут быть очень компактно записаны в геометрических единицах как
Приложения в геометрической теории меры
Зачем нужны дифференциальные уравнения?
Ну и да, не сочтите за навязчивую рекламу, но это же мой пост, всё-таки.
В общем, я уже некоторое время занимаюсь репетиторством. Готовлю школьников к экзаменам, помогаю студентам освоиться в математике. Судя по отзывам, объясняю вполне себе доходчиво и интересно. А сейчас как раз в расписании появилась ещё пара мест для новых людей. Так что, если вдруг вам надо к чему-то подготовиться, что-то подтянуть, понять и т.п., обращайтесь, будем думать =Ъ
порядок изучения основ матанализа у нормальных людей:
1) теория множеств, функции и теория пределов.
2) дифференциальное и интегральное исчисление.
3) ряды
в школе:
1) функции
2) дифференциальное и интегральное исчисление
. Полезные практические знания пришли не от «теоретического трёпа», (как бы нас ни старались обмануть СТАНДАРТНЫМИ попугайскими сказками на эту тему)! «Теорию» подгоняют потом.
Вот если б мне так в школе объяснили, то я бы всё равно ничего не поняла.
Но автору плюсище за попытку обратить гуманитариев в технарей!)
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
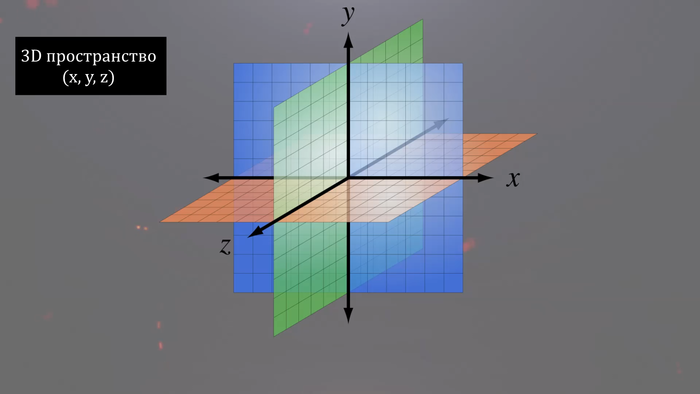
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
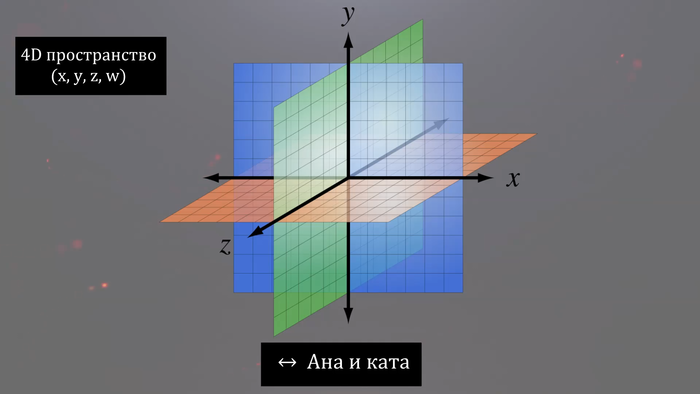
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
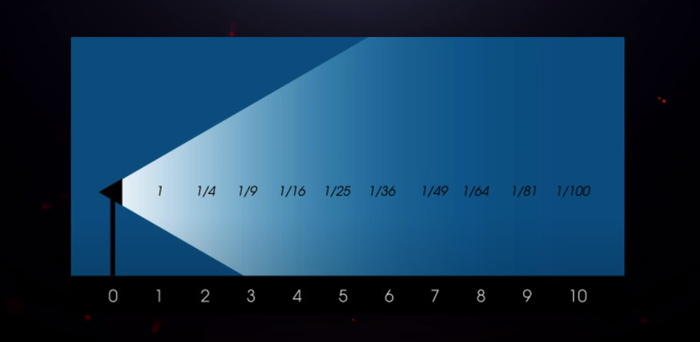
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
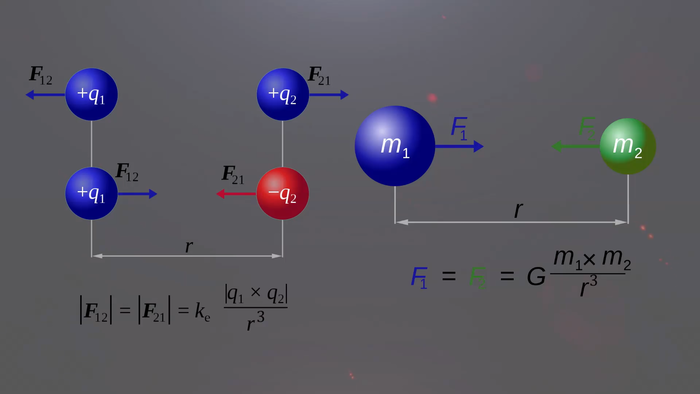
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
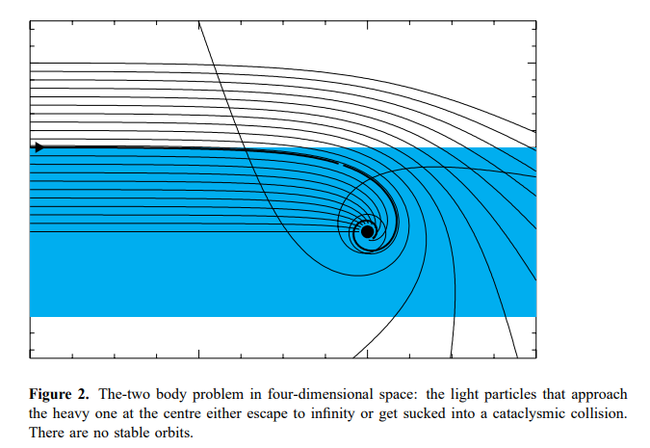
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
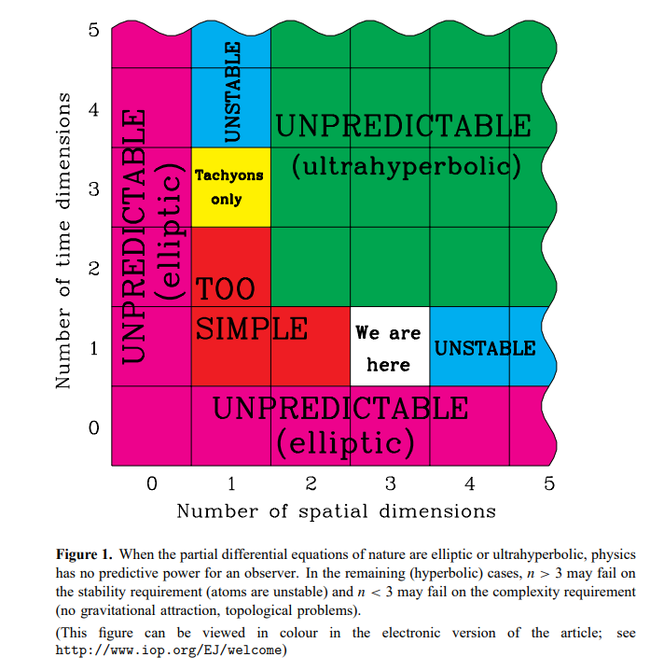
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Зачем нужны дифференциальные формы
В настоящее время данная теория не излагается для студентов технических вузов и даже в общем курсе анализа для менее продвинутых университетов. Для студентов тех специальностей, где анализ функций нескольких переменных не используется, это понятно. Но даже сейчас знание интегрального исчисления нескольких переменных необходимо, например, для студентов физико-технических специальностей, радио- и электротехников, где требуется знание уравнений Максвелла и для теплотехников, где необходим расчет контурных интегралов на PV-диаграммах [1]. В данной статье будет показано преимущество от введения теории внешних форм при изучении интегрального исчисления нескольких переменных по сравнению с существующими курсами. Начнем с простейшего примера – попробуем преобразовать интеграл с помощью замены переменных.
Это кажется настолько очевидным, что студент так же автоматически может попробовать, например, преобразовать двойной интеграл, выразив его в полярных координатах – x=ρcosφ, y=ρsinφ, тогда будет dx=cosφdρ-ρsinφdφ; dy=sinφdρ+ρcosφdφ. Имеем формально:
dxdy=cosφsinφ(dρ) 2 +(ρcos 2 φ–ρsin 2 φ)dρdφ-ρ 2 cosφ sinφ(dφ) 2
Остается спросить, что такое, скажем, интеграл от cosφsinφ(dρ) 2 и… выгнать с экзамена. Понятно, что любой преподаватель знаком со многими подобными примерами.
Теперь, а если студент знает теорию внешних форм? Покажем, как немедленно получается правильная формула.
Здесь, во вводной статье, предполагается, что все нижеследующие понятия уже объяснены, а теоремы доказаны. Все определения и доказательства будут даваться в более подробном учебном курсе [2]. В дальнейшем все криволинейные, поверхностные интегралы заменяются одним видом интеграла – интеграла по гладкому многообразию [3] (кусочно-гладкому) от дифференциальной формы.
Интегралы мы будем брать по т.н. внешним или кососимметричным дифференциальным формам. Форма – это линейная (полилинейная) функция от нескольких векторов, а именно
где ξ и η – произвольные вектора пространства Rm,, а α – число. Количество векторов-аргументов k называется порядком или степенью формы, а сама форма называется k-формой [4]. Кососимметричность означает, что при перестановке двух аргументов форма меняет знак, то есть
Если в каждой точке пространства Rn или в области D этого пространства задана некоторая k-форма, то она называется дифференциальной формой. В разных точках пространства форма в общем случае может быть различной. Важнейшим примером 1-формы может служить обычный дифференциал функции от нескольких переменных. Доказывается, что любая внешняя дифференциальная k-форма (мы будем рассматривать только внешние формы) представляет собой сумму внешних произведений дифференциалов координат типа a(x)dxm∧…dxn, причем по вышесказанному dx∧dy=–dy∧dx, откуда dx∧dx=0 [5]. Здесь мы покажем удобство от введения данного понятия.
Например, в той же задаче о приведении двойного интеграла к новым переменным попробуем перейти к полярным координатам ρ,φ.
dx∧dy=(cosφdρ–ρsinφdφ)∧ ∧(sinφdρ+ρcosφdφ)= cosφsinφdρ∧dρ + +cosρcosφdρ∧dφ–ρsinφsinφdφ∧dρ – –ρsinφρcosφdφ∧dφ=ρcos2φdρ∧dφ– –ρsinφ2dφ∧dρ = (убирая нулевые формы dρ∧dρ и dφ∧dφ ) = ρcos2φdρ∧dφ+ +ρsinφ2dρ∧dφ = (пользуемся антисимметричностью dφ∧dρ=–dρ∧dφ) =ρ dρ∧dφ
Остается выразить f(x,y) через ρ и φ и автоматически сразу получить формулу преобразования двойного интеграла к полярным координатам – якобиан перехода получился «сам» (сейчас студент должен помнить то, что при переходе к новым координатам внутри интеграла появляется якобиан, да и как вычислять определители студенты могут забыть):
Здесь мы не даем явное определение интеграла по форме f(x,y) dx∧dy, но укажем, что он является просто обычным двойным интегралом от функции f на области C изменений переменных x,y, аналогично интеграл справа является двойным интегралом на области изменений переменных ρ и φ.
Введем операцию взятия дифференциала (или внешнего дифференциала) формы, которая будет переводить дифференциальную k-форму в форму степени k+1.
Для формы ω(x)=f(x) нулевой степени (функции в пространстве Rm) дифференциал формы является просто дифференциалом функции f, а именно:
Для внешней формы-одночлена k-й степени
(x точка в Rn) ее дифференциалом будет:
где da(x) – обычный дифференциал функции. От суммы таких форм-одночленов (любая форма, как мы упоминали, представляется в виде суммы таких форм) дифференциал берется по линейности. Ясно, что дифференцирование переводит кососимметричные формы в кососимметричные (в силу свойства внешнего произведения) и повышает степень формы на единицу.
Одно из важнейших свойств дифференциала: d(dω)=0 для любой формы [6] ω.
Теперь приведем несколько примеров, показывающих простоту использования теории внешних форм. Вспомним, например, формулу Грина, связывающую криволинейный интеграл с двойным:
(В данном случае мы не ставим при левом интеграле кружок, означающий замкнутый контур, а границу многообразия C запишем как дC по причинам, которые объясняются в более подробном курсе, хотя прямо сейчас укажем, что граница от границы ддC=0, что тесно связано с равенством ddA=0).
Обычную формулу Грина трудно запомнить (почему, например, стоит знак минуса или почему под скобкой берется частная производная по x от Fy), а, не зная или позабыв вывод, трудно вспомнить саму формулу. Знание теории внешних форм резко упрощает дело. Мы имеем т.н. общую формулу Стокса (Стокса-Пуанкаре) [7]:
где дC – граница многообразия C, F – дифференциальная форма, а dF – ее дифференциал. В данном случае мы не указываемем кратность интегралов, надо только отметить, что она, как и размерность области интегрирования, на единицу меньше для левого интеграла.
Теперь перейдем к доказательству формулы Грина. Найдем дифференциал Fxdx+Fydy,:
d(Fxdx)=
Аналогично d(Fydy) равна (∂Fy)/∂x dx∧dy и окончательно сама формула Грина:
(вспоминая, что интеграл по 2-форме f(x,y) dx∧dy является просто обычным двойным интегралом).
Аналогичный пример для формулы Гаусса-Остроградского:
Имеем, пользуясь кососимметричностью внешнего произведения, в частности, равенством нулю внешнего произведения одинаковых форм:
Наконец, сама формула:
(интеграл по форме Fdx∧dy на поверхности ∂C – это то, что в обычных курсах называется интегралом второго рода, а в правой части интеграл по форме Fdx∧d∧dz будет обычным тройным интегралом, то у нас есть наша искомая формула).
Аналогично выводится и обычная (необобщенная) формула Стокса.
С помощью дифференциальных форм очень легко выражаются понятия векторного анализа, необходимого студентам изучающих электродинамику, гидро- или аэродинамику.
0-форма ω 0 f =f(x) (обычная функция на трехмерном пространстве)
Нетрудно видеть, что любая кососимметричная 0-,1-,2-,или 3-форма представляется однозначно в виде указанных форм с некоторыми f,F,V или ρ [8].
Градиент f – это такой вектор grad f, что
В самом деле, ω 2 rot grad f= dω 1 grad f=dd ω 0 f=0, то есть равенство rot F=0 является необходимым (не достаточным!) чтобы F выражался как grad f. Если F выражается через градиент, то в электродинамике такое поле называется потенциальным.
Также легко доказать, что div rot F=0
В самом деле, ω 3 div rot F= dω 2 rot F=dd ω 1 F=0, то есть равенство div A=0 является необходимым (не достаточным!) чтобы A выражался как rot F. Если div A=0, то в электродинамике такое поле называется соленоидальным.
В заключение заметим, что теория внешних форм не упрощает, хотя и не усложняет, изложение анализа от нескольких переменных. Почему же мы считаем внедрение ее в преподавание в технических вузах определенно полезным, а в некоторых случаях даже совершенно необходимым? Укажем следующие преимущества:
Поэтому можно считать, что если студенту вообще необходимо для конкретных технических дисциплин знание интегрального исчисления нескольких переменных, то ему было бы полезно знать теорию внешних форм, причем учитывая учебные программы для физико-технических, электро- и теплотехнических факультетов уже на первых курсах бакалавриата.
Рецензенты:
Долинер Л.И., д.п.н., профессор, профессор кафедры ИСиТ, УРФУ, ИнФО, г. Екатеринбург;
Матвеева Т.А., д.п.н., профессор, зав. кафедрой ИСиТ, УРФУ, ИнФО, г. Екатеринбург.
Работа поступила в редакцию 29.07.2014.
1 А также диаграмм в других координатах, например T,S (где T–температура, а S–энтропия).
2 Для читателя статьи все нужное содержится в книгах [1]-[5] списка литературы.
3 Особой строгости при введении понятия многообразия (с краем или без) в предполагаемом курсе мы не будем придерживаться, но укажем, что 1-многообразием будет кривая, 2-многообразием – поверхность.
4 Нельзя путать степень формы k с размерностью векторного пространства m.
5 У нас дифференциал координаты dxi (i – здесь индекс, а не показатель степени!) – это функция, сопоставляющая вектору его i-ю координату. Очевидно, что это форма первой степени.
6 Формы, дифференциал которых равен нулю, называются замкнутыми, формы, являющиеся дифференциалом других форм, – точными. Согласно вышесказанному, все точные формы замкнуты, но, как правило, не наоборот.
7 Доказательство этой формулы представляет собой самую сложную часть теории, но обратим внимание читателя на предельную простоту самой этой формулы!
8 Для 2- и 3-форм только в обычном трехмерном пространстве.