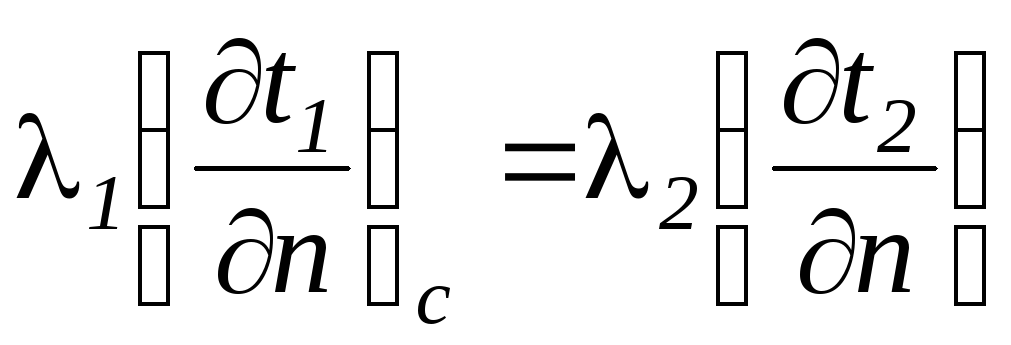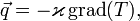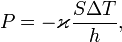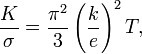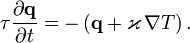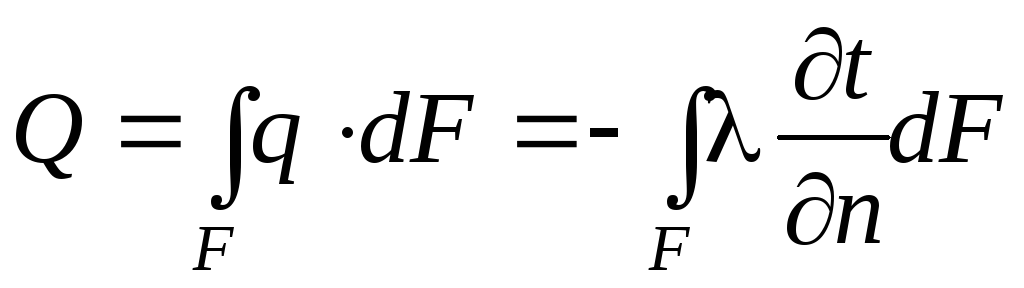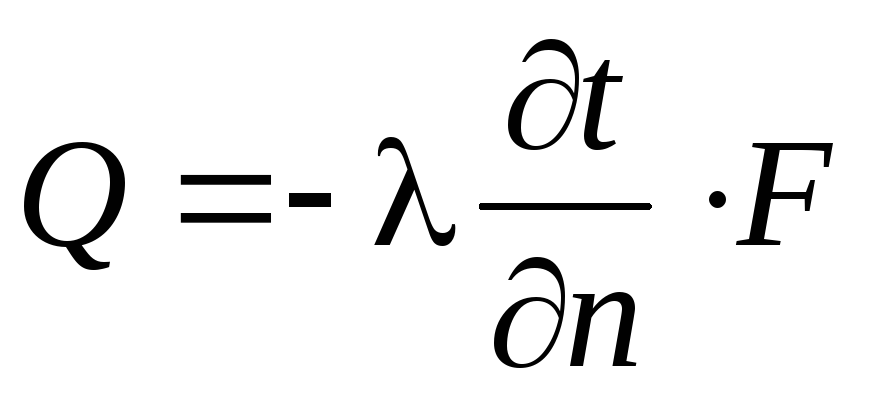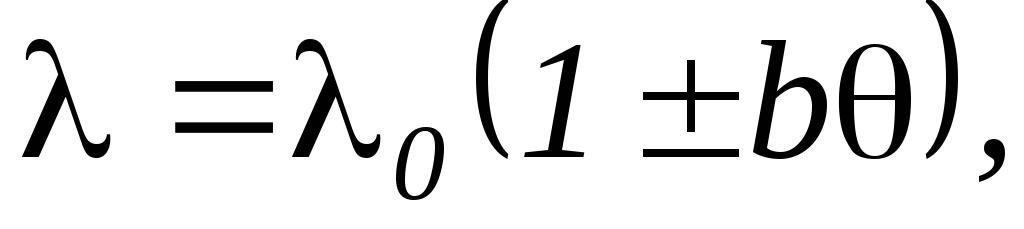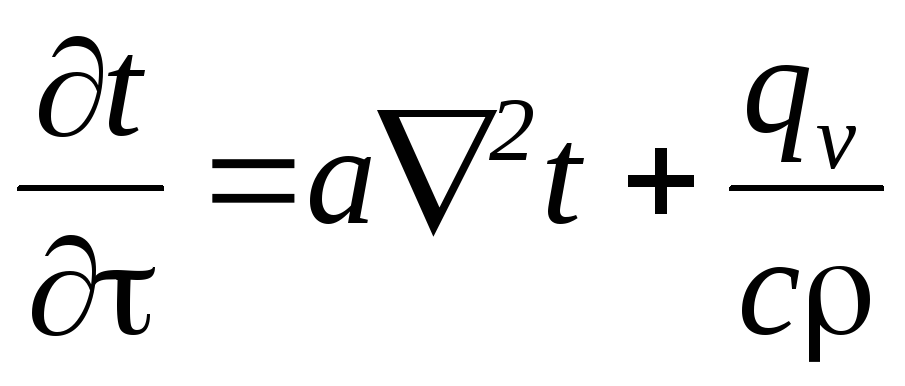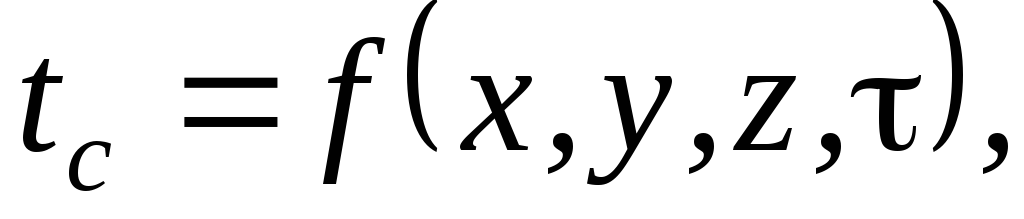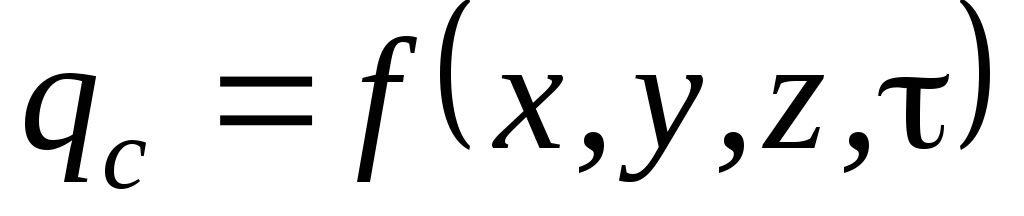закон фурье в дифференциальной форме

Закон Фурье – основной закон теплопроводности.

В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:

,

где Q – тепловой поток, выражается в Вт;

grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;

S – площадь поверхности теплообмена, м 2 ;

Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:

,

где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.

Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.

Закон Фурье для поверхностной плотности теплового потока принимает вид:

.

Знак « минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.

И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики высокочастотных процессов таких как, к примеру, распространение ультразвука, ударной волны.

Источник

Дифференциальное уравнение теплопроводности Фурье

Дата добавления: 2015-06-12 ; просмотров: 5906 ; Нарушение авторских прав

Сущность закона Фурье заключается в утверждении, что количество теплоты, проходящей через выделенную на изотермической поверхности элементарную площадку dF, определяется величиной температурного градиента в рассматриваемом месте:

,

где — вектор теплового тока, которым определяется количество протекшей теплоты, отнесенное к единице площади изотермической поверхности и единице времени; — коэффициент теплопроводности, — градиент температуры.

В дифференциальной форме уравнение теплопроводности выглядит следующим образом:

,

здесь — коэффициент температуропроводности вещества (представляет собой отношение коэффициента теплопроводности к объемной теплоемкости ).

Дифференциальное уравнение теплопроводности, определяющее температурное поле твердого тела, выражает связь между изменением температуры во времени и ее распределением в пространстве. Левая часть уравнения характеризует скорость изменения температуры некоторой точки тела со временем, правая – пространственное распределение температуры вблизи этой точки.

Дифференциальное уравнение Фурье описывает весь класс явлений теплопроводности. Однако в нем не отражены частные особенности конкретных явлений. Для решения конкретной задачи необходимо задать дополнительные условия, которые в совокупности с дифференциальным уравнением однозначно определяют единичное явление. Такие условия называются условиями однозначности:

1. Геометрические свойства (размеры, форма, конфигурация).

2. Физические свойства (коэффициенты , , и т.д.).

3. Временные (начальные) условия (задаются в форме распределения температуры в теле для некоторого момента времени, принимаемого за начальный).

4. Граничные условия (условия взаимодействия со средой, т.е. условия на границах тела; могут быть заданы в различной форме в зависимости от объема предварительных сведений о процессе).

а) Граничное условие первого рода – задается температура поверхности тела.

б) Граничное условие второго рода – задается тепловой поток на поверхности тела.

в) Граничное условие третьего рода – задаются температура окружающей среды и закон теплообмена между поверхностью тела и средой. Выражает требование, чтобы количество теплоты, подходящей изнутри тела к его поверхности с помощью теплопроводности, равнялось количеству теплоты, которая теряется с его поверхности тела в окружающую среду.

Источник

Дифференциальное уравнение теплопроводности.. (Дифференциальное уравнение Фурье)

(Дифференциальное уравнение Фурье)

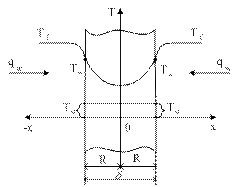
Если поместить тело, например, бесконечную пластинку толщиной δ и начальной температурой T₀ в горячую среду с температурой T_f (рис. 1.1), то пластинка, получая энергию от горячей среды, будет нагреваться, и ее температура изменяется с течением времени в каждой точке.

Рис. 2.1. Нагрев пластины в среде с температурой T_f

Температурное поле, т.е. распределение температур в пространстве и во времени, находят решением дифференциального уравнения (ДУ) теплопроводности, которое в 1814 году вывел французский ученый Фурье и поэтому это уравнение носит его имя. Вывод ДУ теплопроводности основан на законе сохранения энергии и использует закон Фурье. Уравнение Фурье моделирует процессы, которые в процессе теплопроводности протекают в каждом элементарном объеме тела:

1) поглощение тепловой энергии при нагреве или выделение при охлаждении;

2) прохождение теплоты через элементарный объем транзитом;

3) выделение или поглощение теплоты за счет действия внутренних источников или стоков теплоты мощностью q_v.

В векторной форме записи дифференциальное уравнение теплопроводности имеет вид:

,

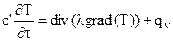
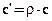
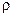
где – удельная объемная теплоемкость, Дж/(м 3 ×К);– плотность, кг/м 3 ; с – удельная массовая теплоемкость, Дж/(кг×К).

Напомним, что для твёрдых тел .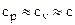

Решая это уравнение, мы получим температурное поле: Т(х_i, t). Т.о. дифференциальное уравнение теплопроводности устанавливает связь между пространственным и временным изменениями температуры.

Вид формул для операторов дивергенции (div) и градиента (grad) зависят от выбора системы координат. Например, в декартовой системе координат ДУ теплопроводности примет вид:

,

или принимая допущение о независимости физических свойств вещества от температуры <>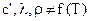

,

где 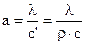– коэффициент температуропроводности, м 2 /с.

В нашем кратком курсе ТМО будем решать дифференциальное уравнение Фурье для тел простейшей формы (бесконечная пластина, бесконечный цилиндр и шар или сфера) с постоянными физическими коэффициентами:

,

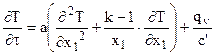
где x₁ – первая координата в ортогональной системе координат: x₁ = xв декартовой системе координат,x₁= r в цилиндрической и сферической системах координат; k = 1, 2 или 3 – коэффициент формы тела: k = 1 – бесконечная пластина; k = 2 – бесконечный цилиндр; k = 3 – шар.

При отсутствии в системе внутренних источников\стоков теплоты (q_v = 0) дифференциальные уравнения Фурье для тел простейшей формы записываются следующим образом:

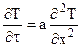
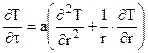
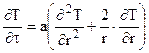
k = 1 :; k = 2 : ;k = 3 : .

При неизменных условиях теплообмена (постоянных температурах флюида, омывающих тело с разных сторон, и постоянных коэффициентах теплоотдачи) на границах тела его температурное поле с некоторого момента времени перестает изменяться во времени и наступает стационарный режим теплопроводности, который для тел простейшей формы описывается уравнением Пуассона при действии внутренних источников теплоты

,

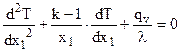
или уравнением Лапласа, если q_v =0

.

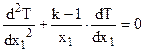
В результате решения одномерного дифференциального уравнения для стационарного процесса теплопроводности находят температурное поле в виде T(x₁) или в явном виде T(x) – в декартовой системе координат и T(r) – в цилиндрической и сферической системах координат.

§4. Условия однозначности,

Источник

Закон Фурье

Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.

В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:

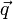
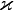
где — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Это выражение известно как закон теплопроводности Фурье.

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.

Коэффициент теплопроводности измеряется в Вт/(м·K).

Содержание

Коэффициенты теплопроводности различных веществ

На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).

Коэффициент теплопроводности вакуума

Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.

Связь с электропроводностью

Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:

Обобщения закона Фурье

Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.

Источник

29. Теплопроводность. Закон Фурье. Коэффициент теплопроводности

Теплопроводность представляет собой форму передачи теплоты путем непосредственного соприкосновения отдельных частиц тела, имеющих различную температуру. При этом процесс теплообмена происходит вследствие передачи энергии микродвижения одних элементарных частиц другим.

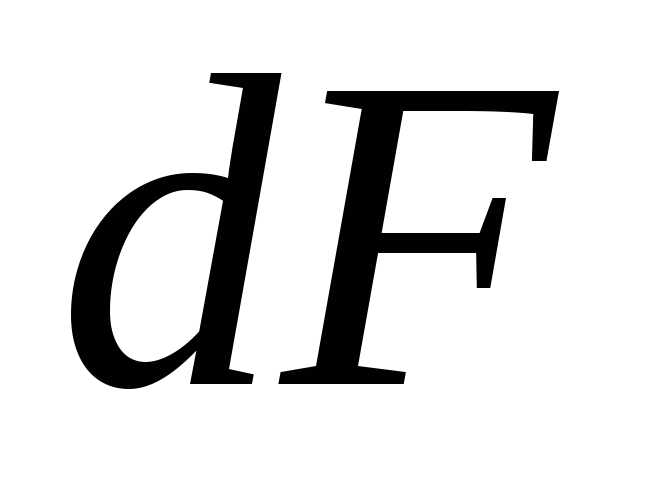
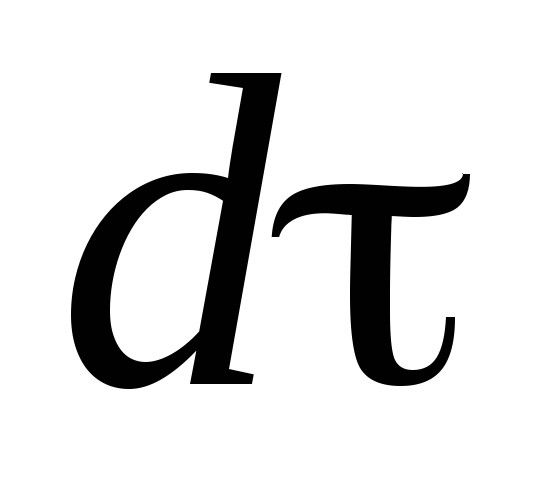
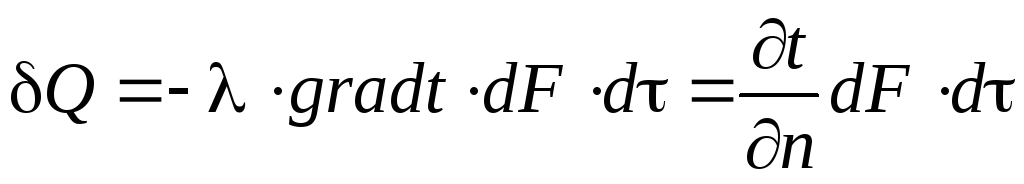
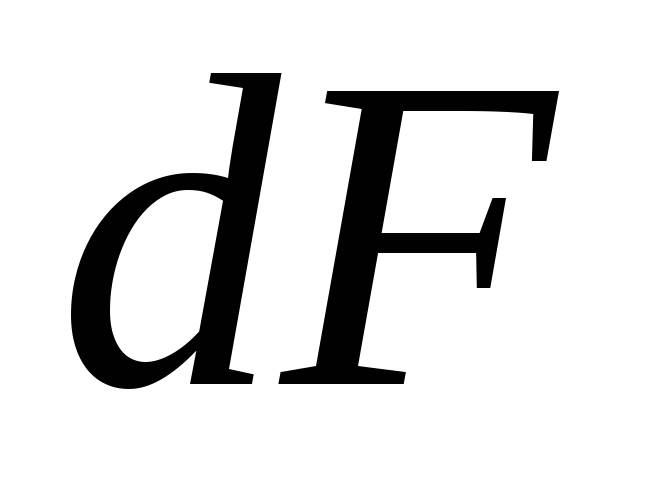
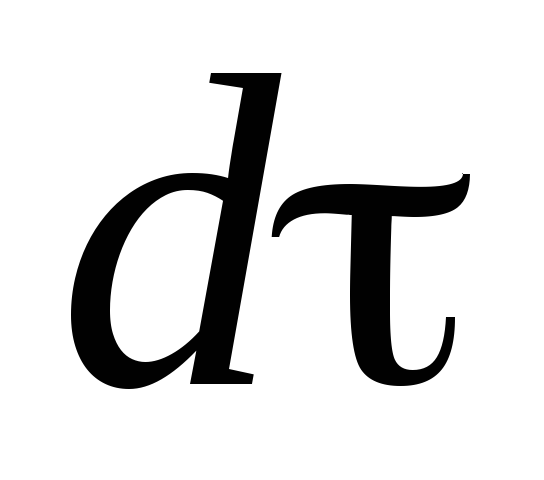
Согласно гипотезе Фурье, количество теплоты проходящей через элемент изотермической поверхности за промежуток времени , пропорционально температурному градиенту , где–коэффициент теплопроводности, – элементарная площадь поверхности, м 2 ; – время передачи теплоты,

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности 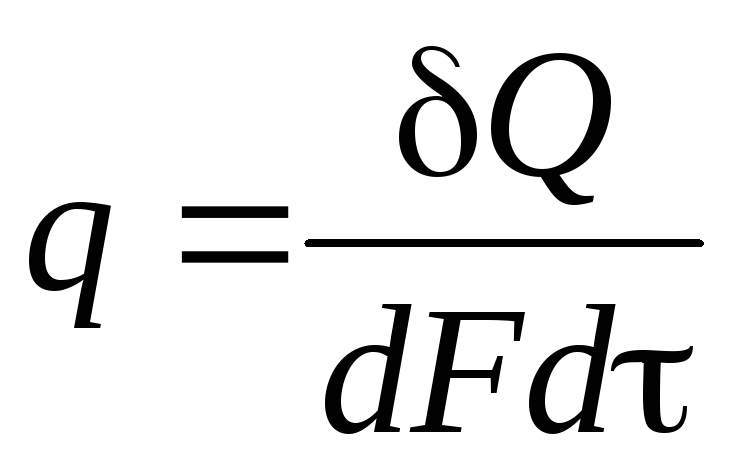, называетсяплотностью теплового потока.

Количества теплоты , проходящее в единицу времени через изотермическую поверхность, называетсятепловым потоком (Дж/с =Вт):

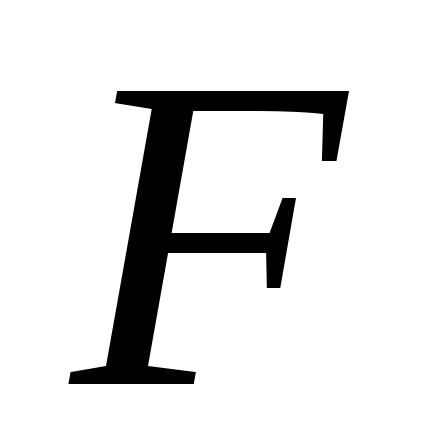
Величина теплового потока и плотность теплового потока являются векторами, за положительное направление которых принимают направление по нормали к изотермической поверхности в сторону уменьшения температуры.

Скалярная величина вектора плотности теплового потока будет равна: Скалярная величина векторатеплового потока будет равна: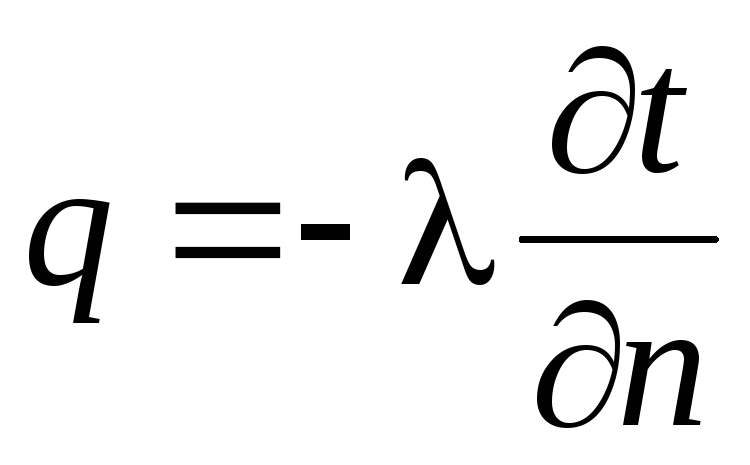

Знак минус в правой части уравнений указывает на то, что тепловой поток и температурный градиент как векторы имеют противоположные направления.

Для каждого тела имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Численное значение определяется опытным путем (в справочных таблицах). При выводе уравнения принято, чтоне зависит от температуры. Как показывают опыты, для многих материалов, зависимость коэффициента теплопроводности от температуры можно принять линейной во всем рассматриваемом интервале т-р:

где – коэффициент теплопроводности при температуре(0°C); b – постоянная, характеризующая приращение (уменьшение) материала при повышении его температуры на1°C.

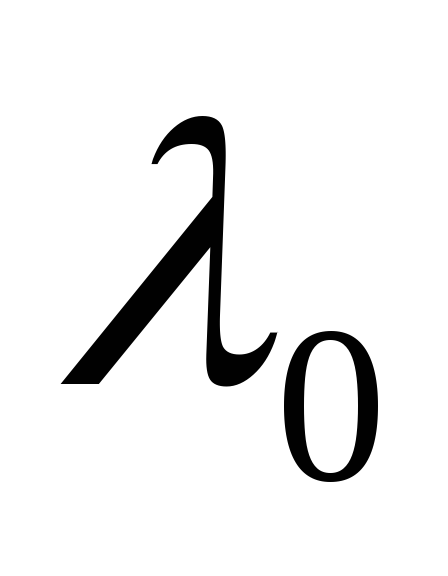
Наилучшими проводниками теплоты являются металлы, у которых Вт/(м·°C). У большей части металлов с возрастанием температуры он уменьшается.

30. Дифференциальное уравнение теплопроводности. Условия однозначности

Распределение температуры в теле, описывается дифференциальным уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:

, где – время,сек; – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела,;

–теплоемкость тела; – плотность тела;– объемная плотность тепловыделения,вm/м 3 ; – температура;– оператор Лапласа.

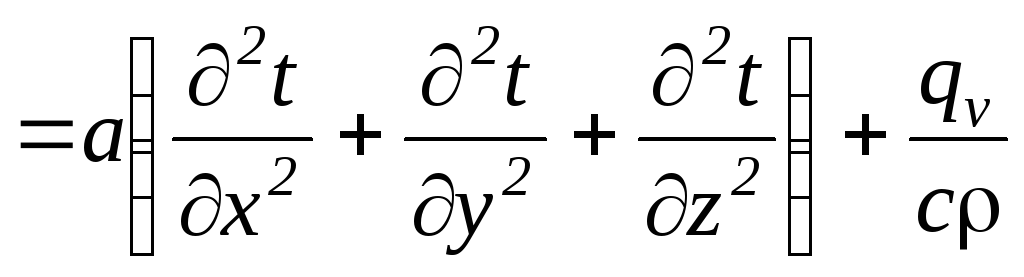
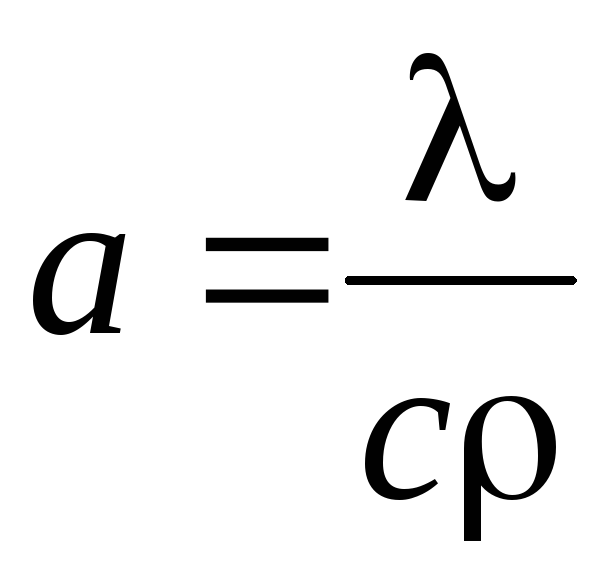
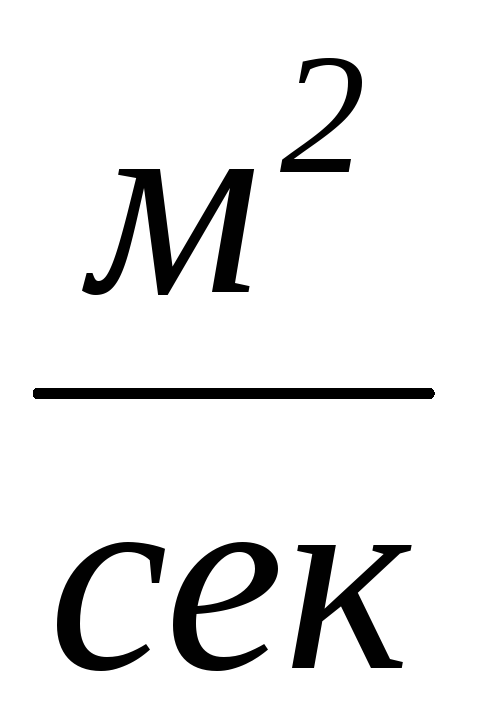
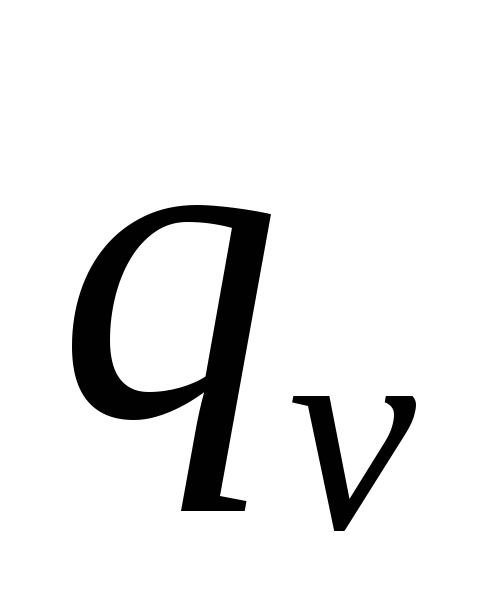
Уравнение называется дифференциальным уравнением теплопроводности.

Чтобы получить конкретное решение уравнения для рассматриваемого случая, необходимо ввести полное математическое описание данного конкретного процесса теплопроводности. Эти частные особенности называются условиями однозначности или краевыми условиями, включающими:

I) Геометрические условия (форма, размеры тела);

II)Физические условия (физические свойства тела и его физические параметры);

III) Начальные условия (распределение температуры в теле в начальный момент времени);

IV) Граничные условия, определяющие взаимодействие тела с окружающей средой.

1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени:

2. Граничные условия второго рода. Задается распределение плотности потока на поверхности тела, как функция координат и времени:

В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем .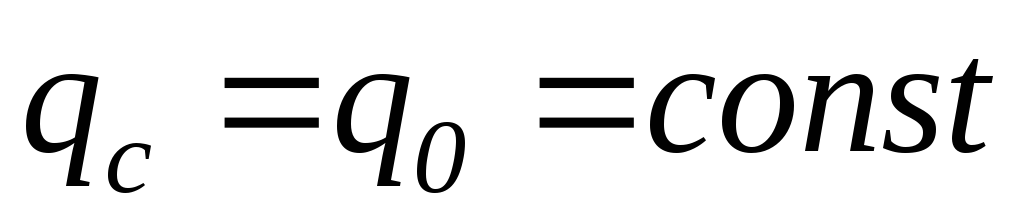

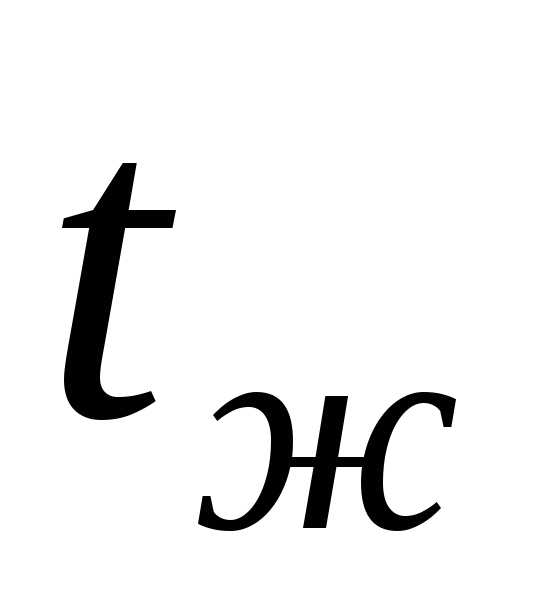
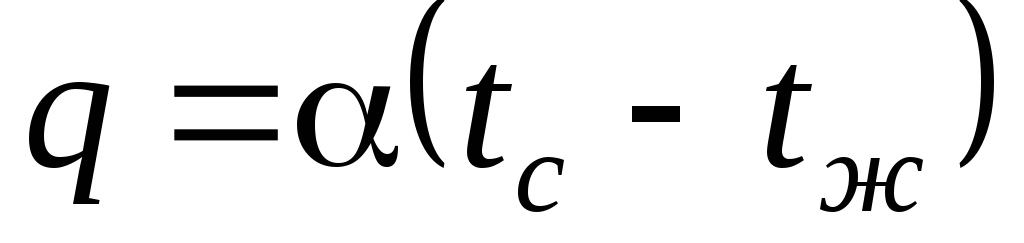
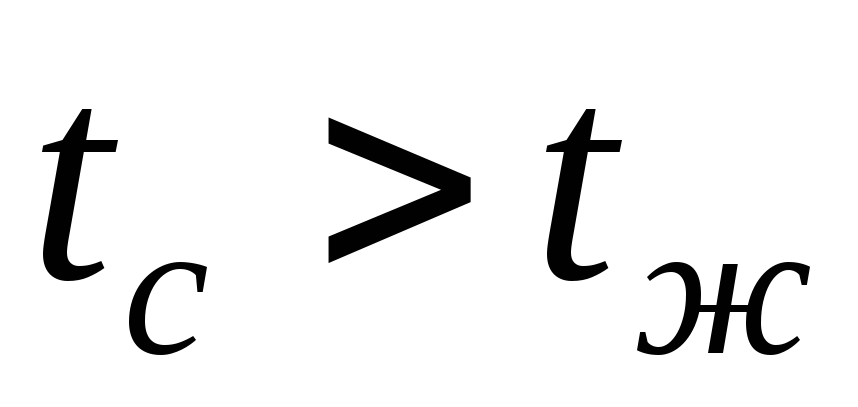
3. Граничные условия третьего рода. Задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой: если , где– коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1 0 С, вm/м 2 град.

4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные коэффициенты теплопроводности. Между телами предполагается идеальный контакт. Тогда , где– коэффициент теплопроводности первого тела;– коэффициент теплопроводности второго тела.

Источник