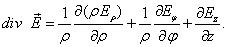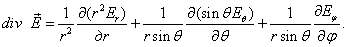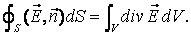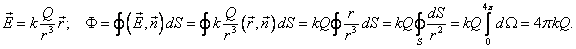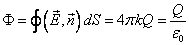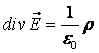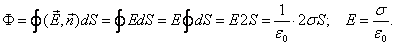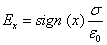закон гаусса в дифференциальной форме

20.03.202303.04.2023 admin 0 Комментариев

Теорема Гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Поток вектора напряженности

Δ Φ = E Δ S cos α = E n Δ S.

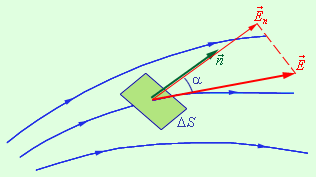
Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Теорема Гаусса. Доказательство

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

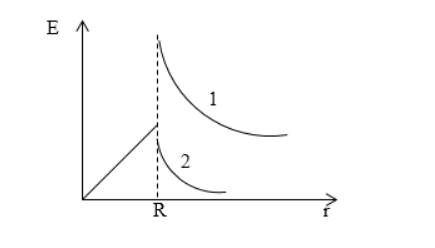
где R является радиусом сферы.

Так, мы доказали теорему Гаусса.

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Применение теоремы Гаусса

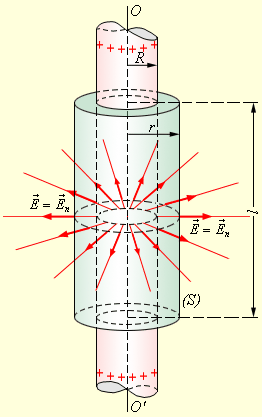
Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

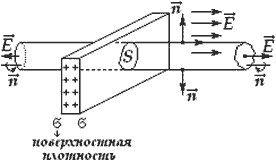
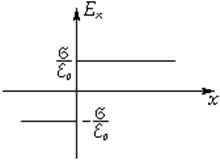
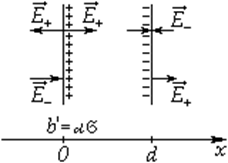
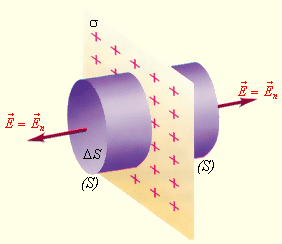
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.

Источник

Закон гаусса в дифференциальной форме

Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля 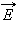через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

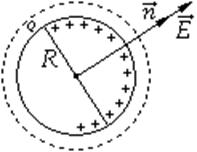
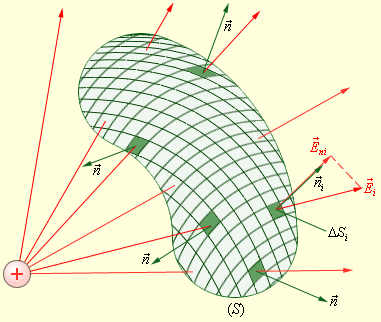
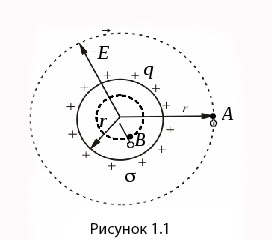
Окружим теперь точечный заряд произвольной замкнутой поверхностью и рассмотрим вспомогательную сферу радиуса (рис. 1.3.3).

Таким образом, теорема Гаусса доказана.

Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.

Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.

Этот результат не зависит от радиуса заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.

Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.

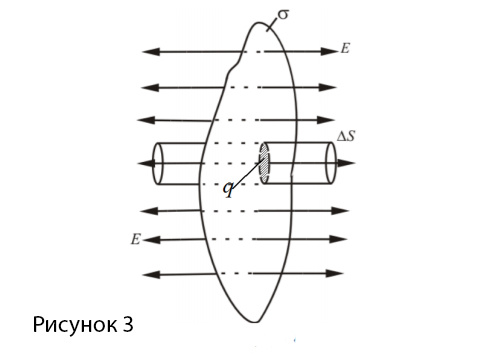
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.

Источник

Расчет теоремы Остроградского-Гаусса для полей в диэлектрике

Теорема Остроградского-Гаусса: история открытия

Теорема Остроградского-Гаусса или теорема о дивергенции — один из основополагающих законов электродинамики, устанавливающий связь между электрическими зарядами и электрическим полем.

В отличие от закона Кулона теорема Остроградского-Гаусса позволяет выразить свойства электростатического поля в более общей форме.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В этом заключается суть теоремы Остроградского-Гаусса. Ее можно сформулировать как совокупный поток напряженного электрического поля, проходящий через плоскость, окружающую заряд, пропорционален величине заряда.

Теорема активно используется в электродинамике, а для более сложных полевых теорий, существуют ее обобщения и аналоги.

Теорема была выведена двумя учеными независимо друг от друга. Российский математик Михаил Остроградский в 1828 году вывел теорему, применимую для векторного поля любой природы, а то время как его немецкий коллега Карл Гаусс, увлекшись изучением магнетизма и электрических полей, представил миру свою теорему применительно к электростатическому полю.

Михаил Остроградский доказал теорему электростатики через уравнение дифференциальной формы, в то время как Карл Гаусс в 1839 году получил аналогичный результат в интегральной форме.

Физический смысл формулы

Физический смысл формулы сводится к тому, что поток электрической индукции ( \(D\) ) через любую замкнутую поверхность \(S\) пропорционален суммарному заряду, заключенному внутри этой поверхности ( \(q\) ).

Вывод формулы в интегральной форме

\(\phi_E=\int_SE_ndS=\int_s\overrightarrow Ed\overrightarrow S\)

Проекция \(\overrightarrow E\) на направление внешней нормали одинакова на каждой точке поверхности \(S_1\) и вычисляется по формуле:

В таким случае поток через \(S_1\) можно узнать, применив формулу:

Пример

Формула для нескольких зарядов будет записываться следующим образом:

Вывод формулы в дифференциальной форме

Дифференциальная форма теоремы используется для расчета электростатического поля в случае произвольного пространственного распределения зарядов. В этой форме отражена связь между объемной плотностью заряда \(\rho\) и изменением \(\overrightarrow E\) вокруг этой точки пространства.

Используем теорему Остроградского-Гаусса, в соответствии с которой поток вектора \(\overrightarrow A\) через любую замкнутую поверхность равняется интегралу от его дивергенции по объему, охваченному этой поверхностью:

Пример

Этим же способом определяется дивергенция любого векторного поля.

Применение формулы

Формула используется для того, чтобы преобразовать объемный интеграл в интеграл по замкнутой поверхности и наоборот.

Применение теоремы

Для расчета электростатического поля

Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:

Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.

Для плоскости

Рассмотрим применение теоремы для равномерно заряженной плоскости.

Задача

Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.

Для сферической поверхности

Задача

В диэлектрике

Диэлектрики влияют на электрического поле. Это влияние выражается в ответном действии поляризационных зарядов, которые возникают в поле. Исходя из этого теорему Остроградского-Гаусса для тел в вакууме можно видоизменить, прибавив к свободным зарядам поляризационные, и тогда эту теорему можно применять в диэлектрической среде.

Теорема будет выглядеть так: \(\oint_s\overrightarrow Dd\overrightarrow S=\sum_^Nq_i=Q(2)\)

Для расчета магнитного поля

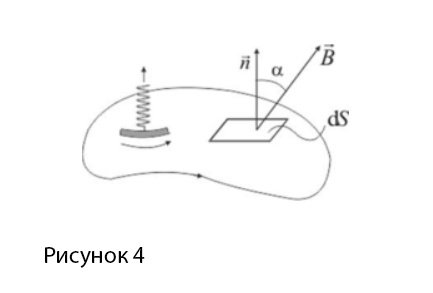
Выделим элементарную бесконечно малую площадку \(dS\) в магнитном поле. Предположим, что она настолько маленькая и плоская, что вектор B можно признать одинаковым по величине и направлению в каждой точке магнитного поля, независимо от того однородно оно или нет.

Определение потока магнитной индукции через произвольную поверхность звучит как сумма потоков через элементарные площадки, на которые разбита эта поверхность, и выражается в виде интеграла по этой поверхности:

Области применения теоремы

Ценность теоремы Остроградского-Гаусса состоит в формулировке общих свойств электрического поля. Она — один из основных постулатов теории электричества. Поэтому широко применяется в общей и учебной физике и таких ее областях как электромагнетизм, электростатика и механика, с ее помощью решают задачи и изучают векторные (в том числе электромагнитные) поля.

Кроме этого теорема применяется в электродинамике, гидродинамике и математическом анализе.

Источник

Теорема Гаусса в присутствии диэлектриков

Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:

Теорема Остроградского-Гаусса

Поток вектора D → через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы D → и E → совпадающие.

Дифференциальная форма теоремы Гаусса выражения ∮ S D → · d S → = ∑ i = 1 N q i = Q изображается как:

Теорема Остроградского-Гаусса вида ∮ S D → · d S → = ∑ i = 1 N q i = Q и d i v D → = ρ справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.

Теорема Остроградского-Гаусса в дифференциальной форме

Напомним формулу вектора электрической индукции:

Произведем подстановку формулы D → = ε 0 E → + P → в d i v D → = ρ :

При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:

Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:

Теорема Остроградского-Гаусса для диэлектриков

Решение

Заряд, находящийся внутри сферы, ищем из формулы:

В результате запишем:

Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: 1 ) все пространство будет заполнено однородным и изотопным диэлектриком, 2 ) произвести замену сферической поверхности на кубическую?

Решение

Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:

Источник

Лекция 4

Ранее была установлена связь между характеристикой электрического поля – напряженностью и его источниками, т.е. зарядами в виде определения напряженности. Существует еще одна связь между ними, которая может оказать существенную помощь при решении симметричных задач – теорема Гаусса. Заметим, что она входит в качестве постулата в систему уравнений Максвелла.

1.Общие замечания о векторном поле

В физике достаточно часто приходится изучать векторные поля (поле скорости жидкости, электромагнитное поле), теория которых достаточно хорошо разработана в математике.

Поле называют векторным, если каждой точке пространства поставлено в соответствии три числа, т.е. вектор.

Векторные поля существенно сложнее скалярных. Вектор поля можно показать с помощью силовых линий. Могут существовать точки, в которых эти линии начинаются и заканчиваются, такие точки называются источниками и стоками. Для электрического поля – это положительный и отрицательный заряд. Где линии гуще – поле сильнее.

Интегральной характеристикой векторного поля является поток вектора поля через какую-то либо поверхность. Дифференциальной или локальной характеристикой векторного поля является дивергенция. Вся терминология пришла из гидродинамики.

2.Понятие потока

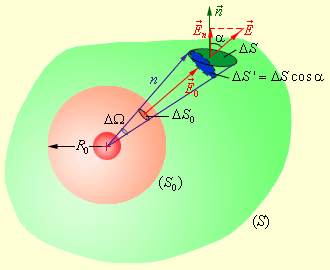
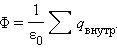
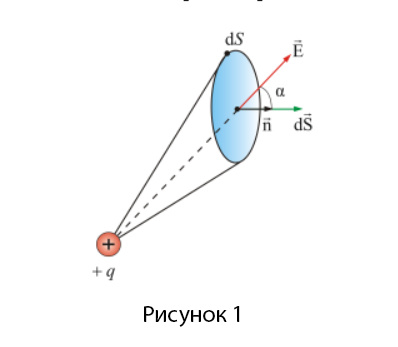
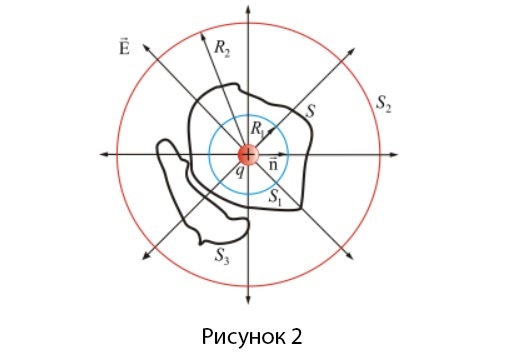
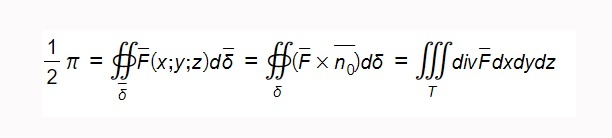
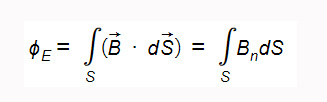
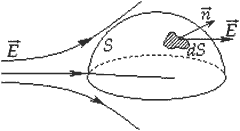
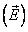Пусть имеется какое-либо векторное поле и некоторая поверхность S. На этой поверхности мы выберем маленькую площадку dS, покажем нормаль к этой точке .

Потоком вектора 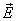через произвольную поверхность площади S называется поверхностный интеграл следующего вида:

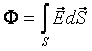или используется ещё обозначение ,где 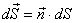– произведение нормали на площадь.

Если поверхность замкнута, то поток через замкнутую поверхность обозначается, как

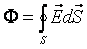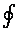где – интеграл по замкнутой поверхности.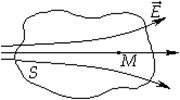

Поток – это объёмная или интегральная характеристика векторного поля.

Возьмем точку M в пространстве. Окружим ее замкнутой поверхностью S и вычислим поток через замкнутую поверхность. Затем поверхность будем стягивать к точке. Понятно, что поток начинает уменьшаться, однако отношение потока к объему, охваченному этой поверхностью, будет конечной величиной – это отношение и называется дивергенцией.

Дивергенцией векторного поля в точке пространства называется следующий интеграл.

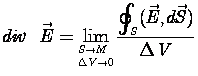, div – дивергенция.