закон инерции для квадратичных форм

Закон инерции квадратичных форм

Установлено, что число отличных от нуля канонических коэффициентов квадратичной формы равно ее рангу и не зависит от выбора невырожденного преобразования, с помощью которого форма A(x, x) приводится к каноническому виду. На самом деле не меняется и число положительных и отрицательных коэффициентов.

Теорема 11.3 (закон инерции квадратичных форм). Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду.

Пусть квадратичная форма f ранга r от n неизвестных x₁, x₂, …, x_n двумя способами приведена к нормальному виду, то есть

f = + + … + – – … – ,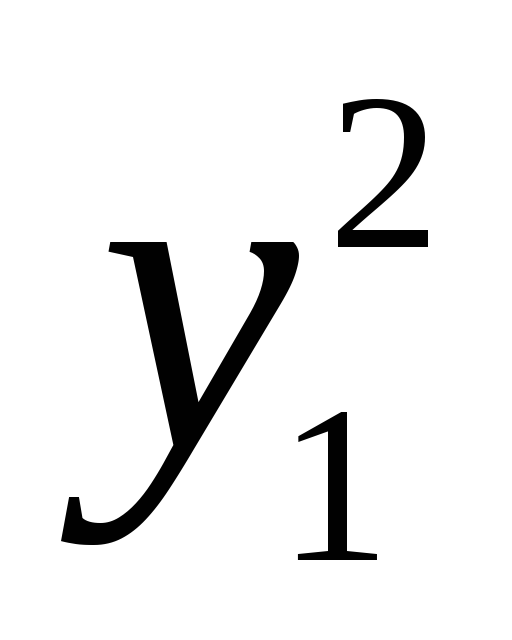

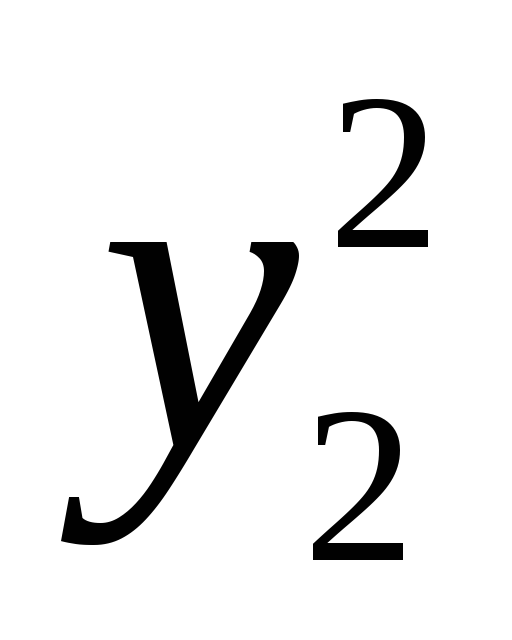
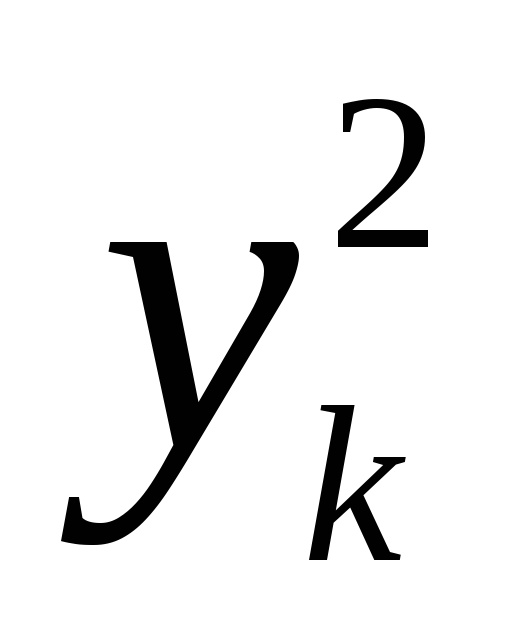
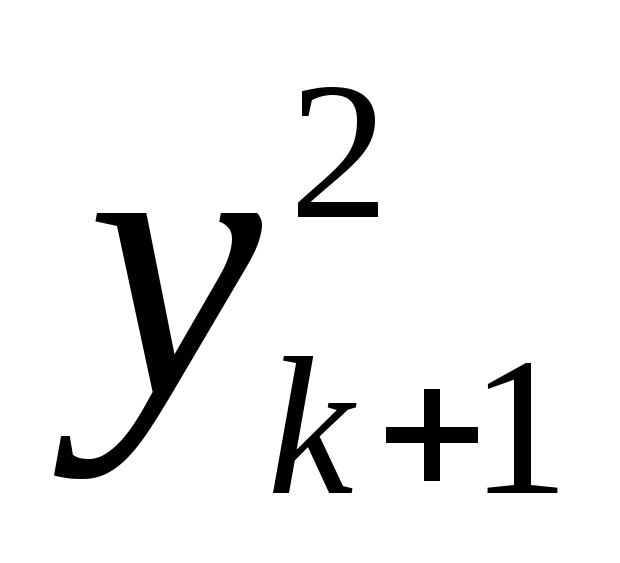
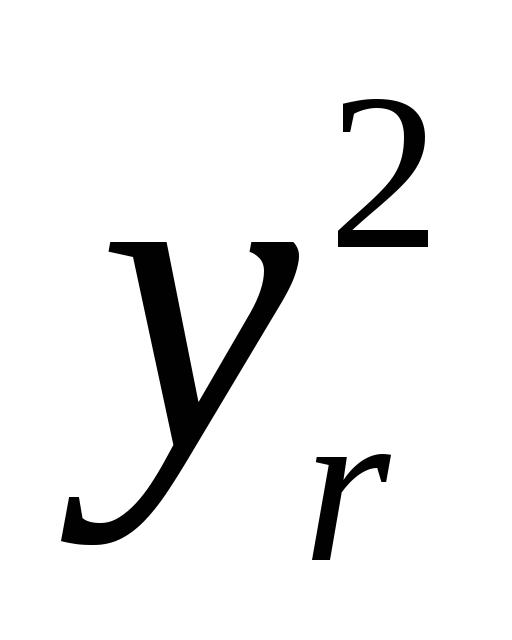
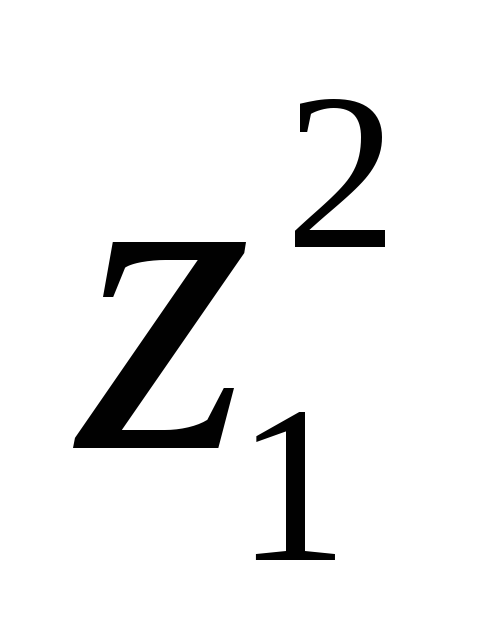
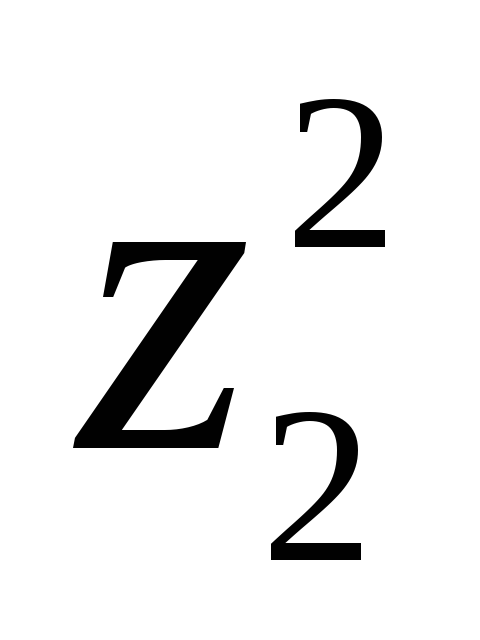
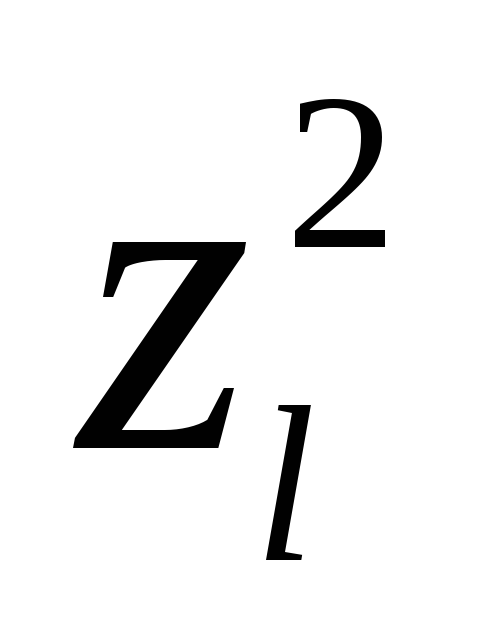
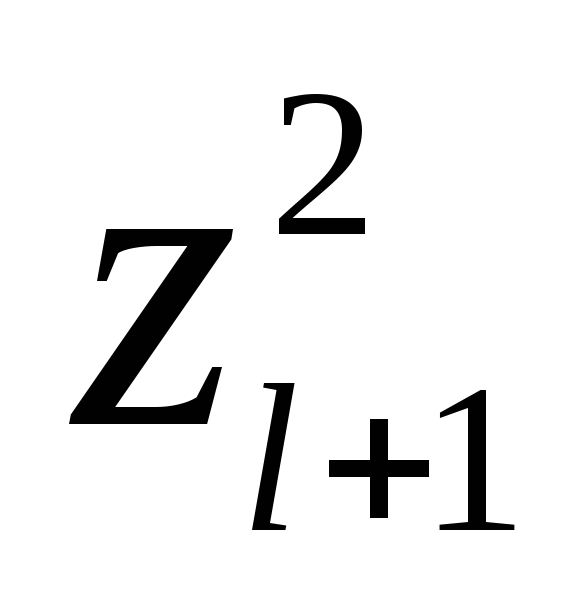
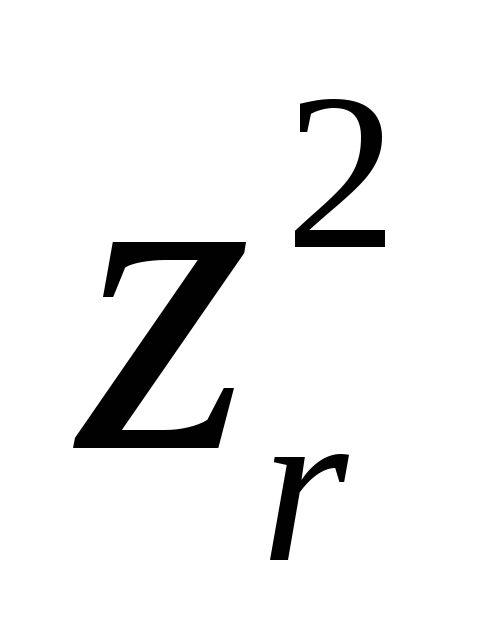
f = + + … + – – … – . Можно доказать, что k = l.

Определение 11.14. Число положительных квадратов в нормальной форме, к которой приводится действительная квадратичная форма, называется положительным индексом инерции этой формы; число отрицательных квадратов – отрицательным индексом инерции, а их сумма – индексом инерции квадратичной формы или сигнатурой формы f.

Если p – положительный индекс инерции; q – отрицательный индекс инерции; k = r = p + q – индекс инерции.

Классификация квадратичных форм

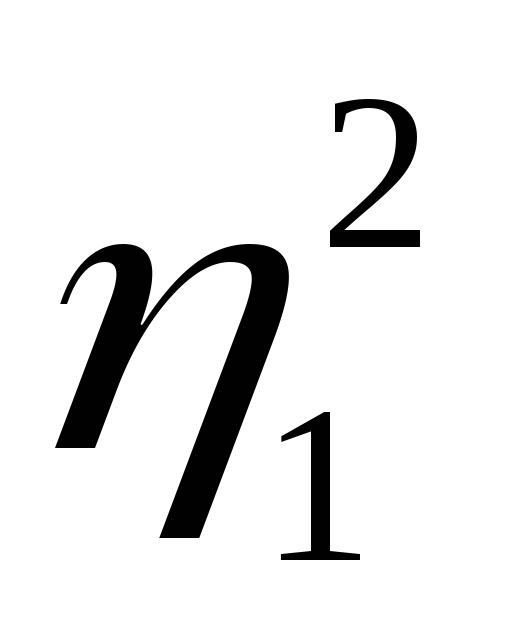
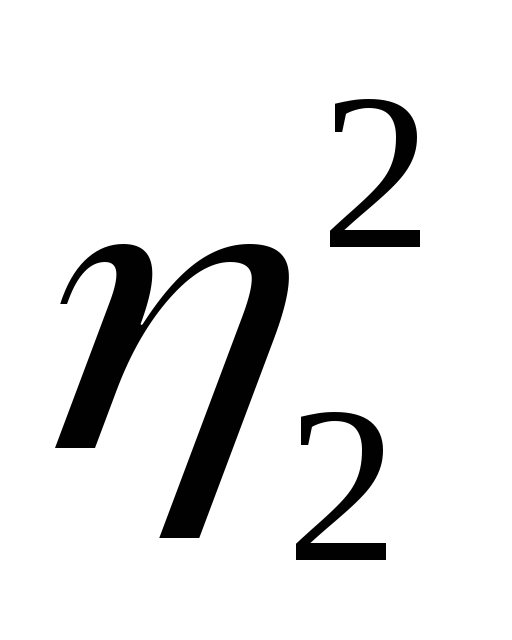
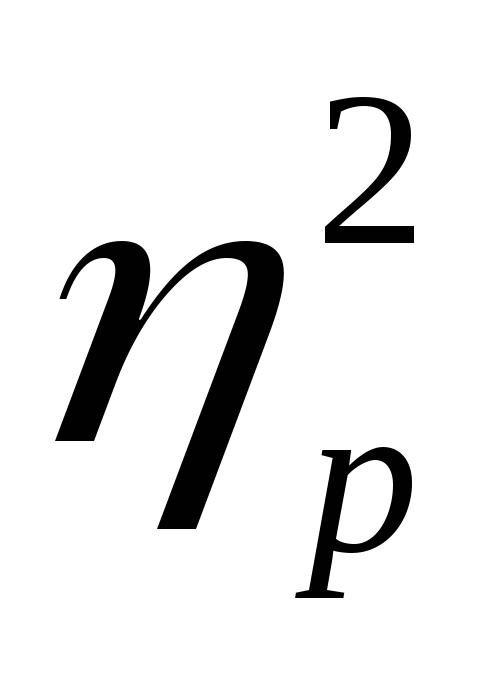
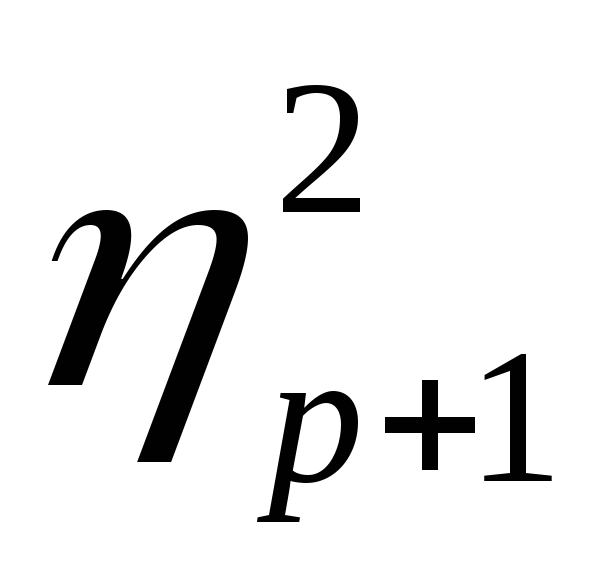
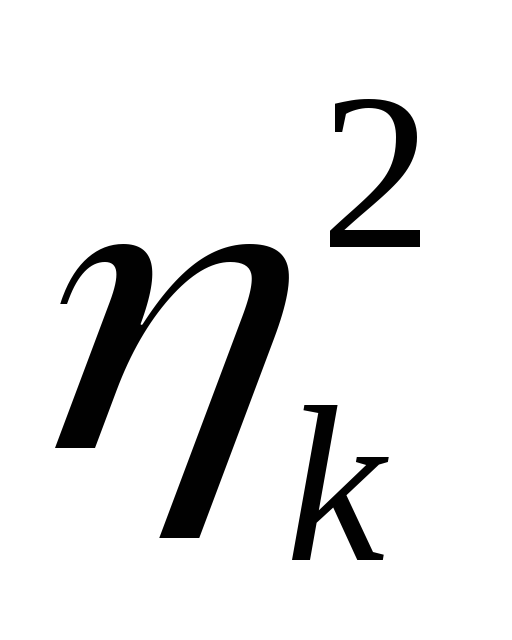
Было доказано, что в любом каноническом базисе f = <f₁, f₂, …, f_n> эта квадратичная форма A(x, x) может быть приведена к нормальному виду A(x, x) = + + … + – – … – , где ₁, ₂, …, _n координаты вектора x в базисе <f>.

Необходимое и достаточное условие знакоопределенности квадратичной формы

Утверждение 11.1. Для того чтобы квадратичная форма A(x, x), заданная в n-мерном векторном пространстве V, была знакоопределенной, необходимо и достаточно, чтобы либо положительный индекс инерции p, либо отрицательный индекс инерции q, был равен размерности n пространства V.

При этом если p = n, то форма положительно определена (то есть для любого x ≠ 0 A(x, x) > 0).

Если же q = n, то форма отрицательно определена (то есть для любого x ≠ 0 A(x, x) 0 и A(y, y) 15 этого не требуется.

Источник

22. Квадратичные формы. Закон инерции квадратичных форм. Критерий Сильвестра.

Однородный многочлен второй степени от п переменных с действительными коэффициентами

, R, (9.1)

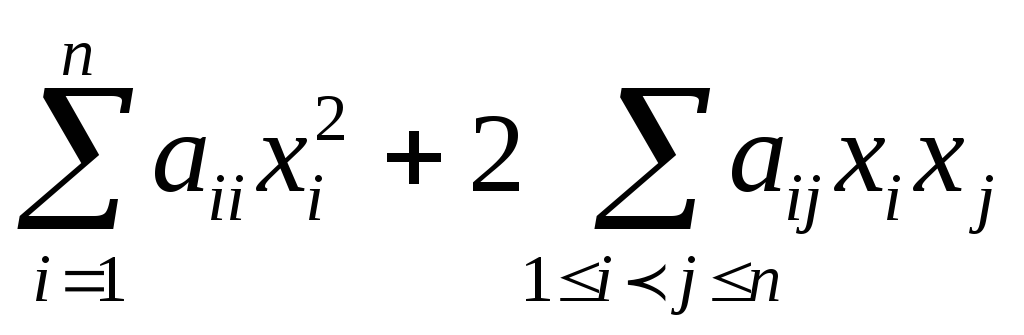
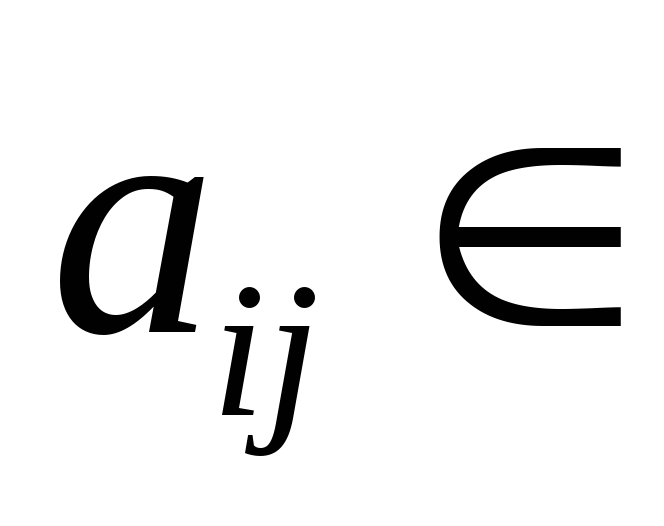
называется квадратичной формой.

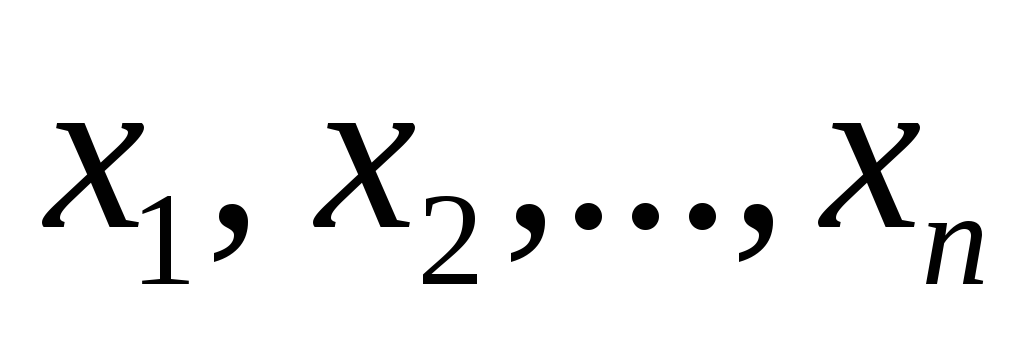
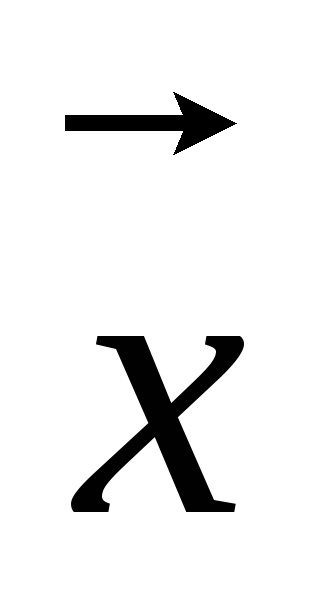
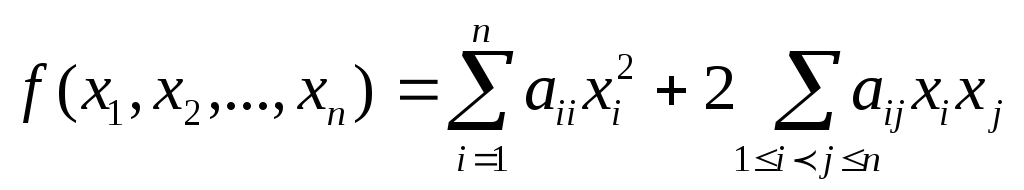
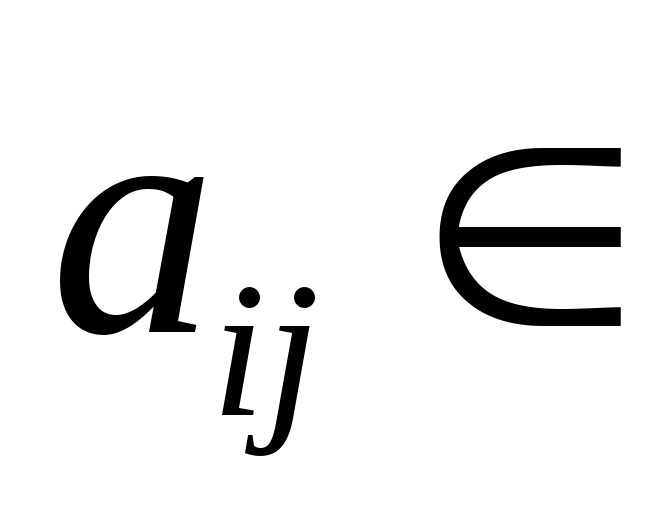
Если в линейном п-мерном пространстве выбрать некоторый базис, то квадратичную форму можно рассматривать как числовую функцию, значение которой определено через вещественные координаты вектора:,R

Если переменные принимают действительные значения иквадратичная форма называется действительной.Матричная запись квадратичной формы

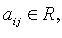
Главные миноры матрицы A называются главными минорами квадратичной формы.

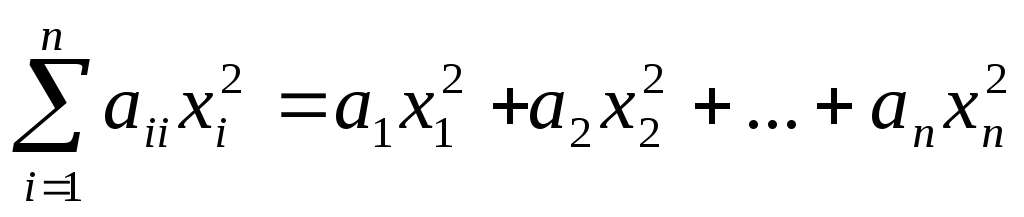
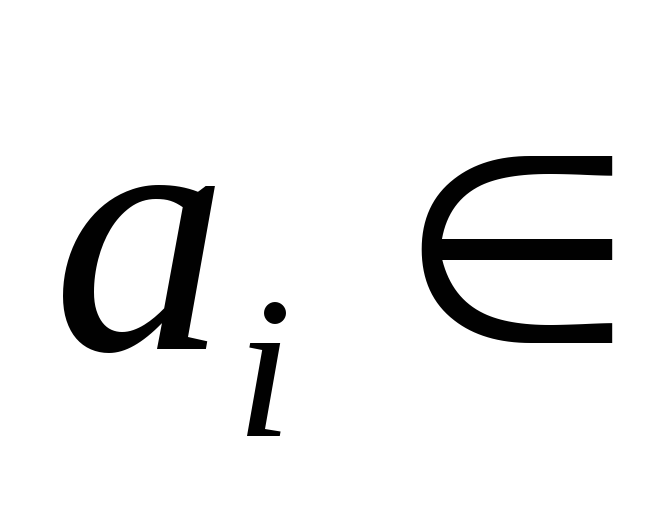
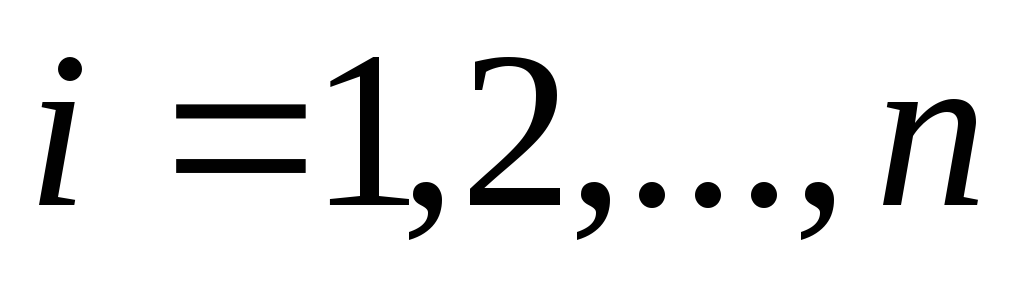
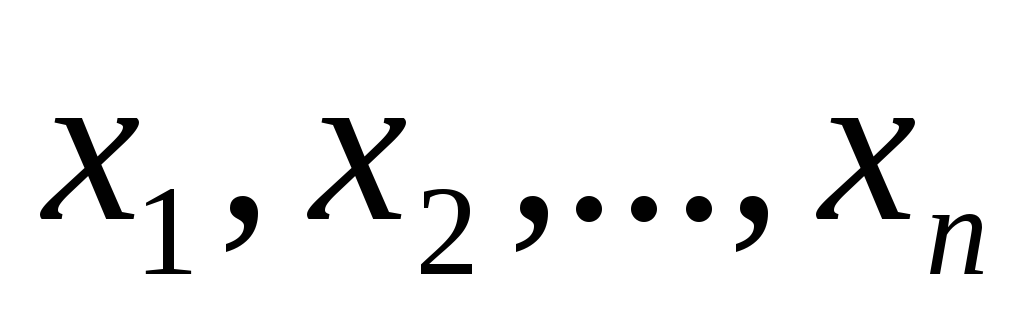
Квадратичная форма ,R, , не имеющая попарных произведений переменных, называется квадратичной формой канонического вида. Переменные, в которых квадратичная форма имеет канонический вид, называются каноническими переменными.

Один из методов преобразования квадратичной формы к каноническому виду путем замены переменных состоит в последовательном выделении полных квадратов. Такой метод называется методом Лагранжа

Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.

Классификация действительных квадратичных форм Положительно-определенные

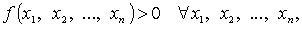
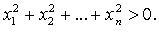
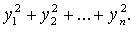
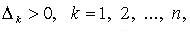
Квадратичные формы, для которых таких, чтоНормальный видКвадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны(критерий Сильвестра).

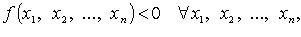
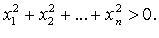
Квадратичные формы, для которых таких, чтоНормальный видКвадратичная форма является отрицательно-определенной тогда и только тогда, когда

Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.

Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу (a_ij). Тогда эта форма положительно определена, если и только если все её угловые миноры Δ_i положительны, отрицательно определена, если и только если их знаки чередуются, причём Δ₁ 13 / 15 13 14 15 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Закон инерции и знакоопределенность квадратичных форм

Закон инерции вещественных квадратичных форм

Рассмотрим вещественные (действительные) квадратичные формы, коэффициенты которых являются действительными числами, а переменные принимают действительные значения. Любую вещественную форму можно привести к каноническому виду

при помощи линейной невырожденной замены переменных с действительной матрицей (см. теорему 6.1 и п.2 замечаний 6.4). Коэффициенты квадратичной формы являются действительными числами.

то получим нормальный вид квадратичной формы

в котором коэффициенты равны либо единице, либо минус единице (переменные входят с нулевыми коэффициентами).

Теорема 6.3 о законе инерции квадратичных форм. Ранг, положительный и отрицательный индексы, а также сигнатура вещественной квадратичной формы не зависят от действительной невырожденной линейной замены переменных, приводящей квадратичную форму к каноническому виду.

Из теоремы 6.3 следует, что два канонических вида одной и той же квадратичной формы имеют:

а) одинаковое количество ненулевых слагаемых (которое определяется рангом квадратичной формы);

б) одинаковое количество слагаемых одного знака.

В самом деле, пусть квадратичная форма ранга приведена к нормальному виду (6.19)

Знакоопределенность вещественных квадратичных форм

Пример 6.11. Исследовать знакоопределенность квадратичных форм

Решение. 1) Выделим полный квадрат по переменной

Следовательно, данная форма положительно определенная.

3) Квадратичная форма неопределенная, так как она может принимать как положительные, так и отрицательные значения. Например, 0,

2. Дискриминант положительно определенной квадратичной формы больше нуля, т.е. 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFMAAAARBAMAAABTDI1UAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAcBBF4GZW9AxsOCC8HGfqzT7AAABcklEQVQoz2NgoAywTMAl80gdTYBNEV2JswOEnvYVQnPCJOwvouvdqgRRywxVKiQAoRn7P6IpjXZgWoCi1AiqVDwXrJSvEKaS8RoD+0+4UkagskVQpd5On8F0RQhUKVAB8z8gzb4o/SsDS1Cbg9XvUAOwTDoTRKkgTC3fHwbmX0A6e8KMrwweC6S2OHcYg93O0sj1GWpxRQqY5gGa+glo6HeQ+fETOL8zKgmAXcBkwAp1PIOAEVgtK0Qp00eQ0v3Gxt+ASsHyRcZmX+EeMlqJMFUWpJTx/5kz4VClLE1KGt/gSq00EUolwEr3g1QpMRaAxAPA4tDwy4SFANAiti8gKn8CgztQqQLQHG8BuFLGIoi3WL6BvMTAco2B7ZuAbwtDMsNaF2CUcLYBvfob4uqKFEYII9uBqwFIzWhV+/+RU1epgGFuBzCw7v9PAOJv4KAKYYS6w0kvG5zYXFgmCjCwTASyQFhQEIRBhvEdQSSCqcDIAQA2IGnMbGi0ggAAAABJRU5ErkJggg==»/>.

4. Для отрицательно (неположительно) определенных квадратичных форм справедливы утверждения аналогичные пунктам 1-3, так как знаки форм и противоположные.

Критерий Сильвестра

Теорема 6.4 (критерий Сильвестра). Для того чтобы вещественная квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все угловые миноры ее матрицы были положительны:

В самом деле, рассмотрим первое утверждение теоремы (о положительной определенности). Достаточность условий (6.20) следует из теоремы 6.3 (теоремы Якоби), так как при выполнении этих неравенств квадратичная форма приводится к каноническому виду

Критерий полуопределенности квадратичной формы

Теорема 6.5 (критерий полуопределенности квадратичной формы). Для того чтобы квадратичная форма была неотрицательно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы были неотрицательны.

Для неположительной определенности квадратичной формы необходимо и достаточно, чтобы все главные миноры ее матрицы удовлетворяли условиям:

Условия (6.22) означают, что главные миноры четного порядка должны быть неотрицательны, а нечетного порядка — неположительны. Для доказательства теоремы используется критерий Сильвестра.

Пример 6.12. Выяснить знакоопределенность квадратичных форм с матрицами

главные миноры первого порядка: ;

главные миноры второго порядка: ;

Источник

Закон инерции для квадратичных форм

Теорема 3. Если квадратичная форма преобразована двумя способами к каноническому виду, то число квадратов новых переменных с положительными коэффициентами будет одинаково, так же как число квадратов новых переменных с отрицательными коэффициентами. Иными словами, число положительных и отрицательных коэффициентов не зависит от способа приведения формы к каноническому виду.

Доказательство. Пусть дана форма, приведенная к каноническому виду двумя способами:

Считаем, что все и 0, положительны. Пусть исходные переменные связаны с новыми посредством следующих невырожденных преобразований:

Допустим, что число положительных коэффициентов не одинаково. Будем считать, для определенности, что Положим . Все — являются линейными формами от . Таким образом, написанная совокупность равенств есть система линейных однородных уравнений относительно . Число неизвестных равно , число уравнений равно . Поэтому система имеет нетривиальные решения. Пусть — одно из них. Соответствующие значения для обозначим через Заметим, что . Соответствующие значения для обозначим через . Эти значения не равны одновременно нулю (иначе равнялись бы нулю ), но . Поэтому среди чисел имеются отличные от нуля.

Из представления имеем:

Из другого представления:

Последнее неравенство строгое, ибо среди имеются отличные от нуля. Мы пришли к противоречию, так что предположение о различии числа положительных коэффициентов неверно.

Для установления равенства числа отрицательных коэффициентов достаточно перейти к форме и ее каноническим представлениям

и применить уже доказанное утверждение о равенстве положительных коэффициентов. Теорема доказана полностью.

Заметим еще, что если

то можно дать формулу для числа отрицательных коэффициентов в канонической форме. Именно, оно равно числу перемен знаков в ряду чисел

Действительно, коэффициенты в канонической форме, получающейся при преобразовании с правой унитреугольной матрицей, равны

так что число отрицательных среди них равно указанному выше числу перемен знаков.

Источник

113. Закон инерции квадратичных форм

Квадратичную форму можно привести к каноническому виду различными способами.

Теорема 1. Любую квадратичную форму с действительными переменными невырожденным линейным преобразованием переменных можно привести к нормальному виду.

Доказательство. Приведем сначала квадратичную форму к каноническому виду (2) §3. Можно предположить что в полученной квадратичной форме канонического вида имеется R коэффициентов неравных нулю, среди которых имеется S положительных коэффициентов и T отрицательных коэффициентов. При этом можно неизвестные перенумеровать и форму канонического вида представить в виде:

,

Где 0 £ S £ R £ N И все коэффициенты С1, с2,…, СR положительны. Тогда невырожденное преобразование переменных

Приводит форму F к нормальному виду,

.

Определение 2. Рангом квадратичной формы называется ранг матрицы квадратичной формы.

Теорема 2. При невырожденных линейных преобразованиях переменных ранг квадратичной формы не меняется. Ранг квадратичной формы равен числу ненулевых коэффициентов в форме канонического вида, т. е. Rang F = S+ T .

Лемма 1. Ранг произведения AB матриц не превосходит ранга каждого из его сомножителей.

Доказательство. Из определения произведения матриц следует, что столбцы матрицы AB являются линейными комбинациями столбцов матрицы A. Тогда столбцы матрицы AB выражаются через базисные столбцы матрицы A. И максимальное число линейно независимых столбцов матрицы AB меньше ранга матрицы A. Отсюда ранг матрицы AB не больше ранга матрицы A.

Из определения произведения матриц следует, что строки матрицы AB являются линейными комбинациями строк матрицы B. Тогда строки матрицы AB выражаются через базисные строки матрицы B. Отсюда ранг матрицы AB не больше ранга матрицы B. 

Лемма 2. Если один из сомножителей A или B квадратная невырожденная матрица, то ранг произведения AB равен рангу другого сомножителя.

Так как форма канонического вида получена из квадратичной формы невырожденным преобразованием переменных, то ранг квадратичной формы равен рангу матрицы квадратичной формы, т. е. равен числу ненулевых коэффициентов в форме канонического вида.

Теорема 3. Число положительных и число отрицательных коэффициентов в форме канонического вида (сигнатура квадратичной формы) не зависит от способа приведения квадратичной формы к каноническому виду.

Доказательство. Допустим, что квадратичная форма F ранга R от N переменных двумя способами приведена к каноническому виду,

, (1)

Где предполагаем, что все коэффициенты СI и DI (I=1,…,N) положительны. Пусть исходные переменные связаны с новыми переменными посредством невырожденных преобразований:

Источник