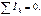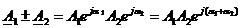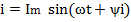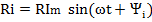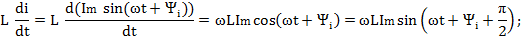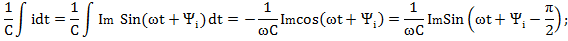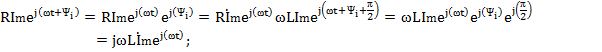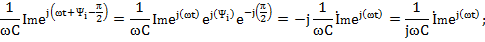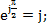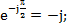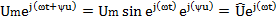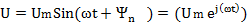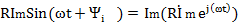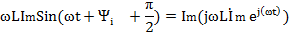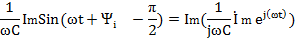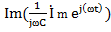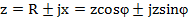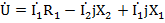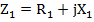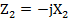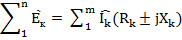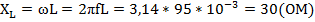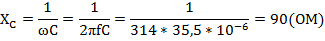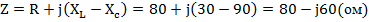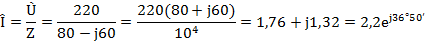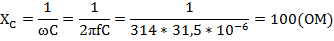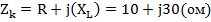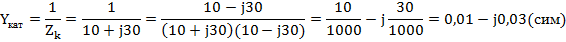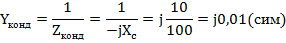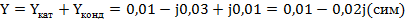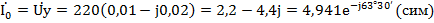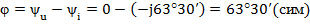закон кирхгофа и ома в символической форме
Закон Ома и Кирхгофа в символической форме
По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е. 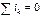
В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.



Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:


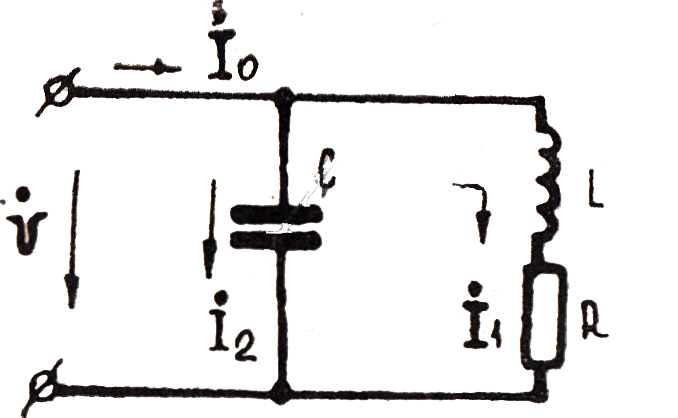
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
 |  |  |
Если  , ,  (по теореме о линейном преобразовании), то (по теореме о линейном преобразовании), то  . Это закон Ома в символической форме. . Это закон Ома в символической форме. |    (по теореме о производной) Закон Ома: (по теореме о производной) Закон Ома:  . . |   (по теореме об интеграле) Закон Ома: (по теореме об интеграле) Закон Ома:  . . |
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
 |  |  |
Дата добавления: 2015-04-16 ; просмотров: 98 ; Нарушение авторских прав
Закон Ома и законы Кирхгофа для мгновенных значений токов и напряжений. Законы Ома и Кирхгофа в символической и операторной формах.
Первый закон Кирхгофа. Алгебраическая сумма мгновенных токов, притекающих к узлу равна нулю.
Заметим, что первый закон Кирхгофа можно сформулировать и так: сумма мгновенных токов, притекающих к узлу, равна сумме токов, вытекающих из этого узла. В более общей форме: алгебраическая сумма токов, притекающих к произвольному сечению, равна нулю.
Пример. Записать первый закон Кирхгофа для следующего узла (рис. 1.14.2).
Решение. 
Второй закон Кирхгофа для мгновенных величин. Алгебраическая сумма мгновенных падений напряжений в контуре равна алгебраической сумме мгновенных ЭДС в этом контуре.
где n – количество пассивных элементов в контуре;
m – количество источников ЭДС в контуре.
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
Для последовательно соединенных элементов формула импеданса имеет следующее значение:
При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:
При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:
Операторная запись законов Кирхгофа
При ненулевых начальных условиях II закон Кирхгофа можно записать
Величина, обратная комплексному сопротивлению, – комплексная проводимость:
Законы киргофа в символической форме:
Согласно первому закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:
Подставив вместо ik в (2.63) Íkejωt и вынеся ejωt за знак суммы, получим ejωtΣÍk=0. Так как ejωt не равно нулю при любом t, то:
Уравнение (2.63,а) представляет собой первый закон Кирхгофа в символической форме записи.
Пусть замкнутый контур содержит n ветвей и каждая k- ветвь в общем случае включает в себя источник ЭДС ek, резистор Rk, индуктивную катушку Lk и конденсатор Ck, по которым протекает ток ik.
Тогда по второму закону Кирхгофа:
Но каждое слагаемое левой части можно заменить на ÍkZk, а каждое слагаемое правой части – на Ék. Поэтому уравнение примет вид:
Уравнение (2.65) представляет собой второй закон Кирхгофа в символической форме записи.
Изображение синусоидальных ЭДС, напряжений и токов с помощью вращающихся векторов и комплексных чисел. Формулы Эйлера для комплексных чисел. Сложение, вычитание, умножение, деление синусоидальных функций времени. Векторная диаграмма.
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

показательной
тригонометрической 
алгебраической 
Например, ЭДС 

Фазовый угол 

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
 , , | (4) |
Рис.2.7. Векторное изображение синусоидальных ЭДС
Рис.2.8. Векторное изображение синусоидальных значений напряжения и тока, имеющих угол сдвига фаз
На рис. 2.9 и 2.10 показано сложение и вычитание векторов на векторных диаграммах. Здесь сложение двух синусоид 


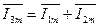

Изображение синусоидальных величин на комплексной плоскости осуществляется комплексными числами.
Данная формула связывает комплексную экспоненту с тригонометрическими функциями:
Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:

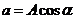
При сложении и вычитании комплексных чисел удобно пользоваться алгебраической формой записи:
При умножении, делении, возведении в степень удобно пользоваться показательной формой
Если комплексное число 

Синусоидальное ЭДС можно представить комплексным числом:
1.4. Законы Ома и Кирхгофа
1.4. Законы Ома и Кирхгофа
Закон Ома для всей цепи выражает соотношение между электродвижущей силой (ЭДС), сопротивлением и током. Согласно этому закону ток в замкнутой цепи равен ЭДС источника деленной на сопротивление всей цепи:

где I – ток, протекающий по цепи;
E – ЭДС, генератора, подключенного к электрической цепи;
Rг – сопротивление генератора;
Rц – сопротивление цепи.
Закон Ома для участка цепи. Ток на участке цепи прямо пропорционален напряжению между началом и концом участка и обратно пропорционален сопротивлению участка. Аналитически закон выражается в следующем виде:

где I – ток, протекающий на участке цепи;
R – сопротивление участка цепи;
U – напряжение на участке цепи.
Обобщенный закон Ома. Сила тока в контуре цепи прямо пропорциональна алгебраической сумме ЭДС всех источников цепи и обратно пропорциональна арифметической сумме всех активных сопротивлений цепи.

где m и n – количество источников и резисторов в контуре цепи.
При алгебраическом суммировании со знаком “плюс” берутся те ЭДС, направление которых совпадает с направлением тока, а со знаком “минус”– те ЭДС, направление которых не совпадает с направлением тока.
Первый закон Кирхгофа. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 1.10 представлена простейшая разветвленная цепь.
Рис. 1.10 Схема разветвленной цепи.
Разветвленной называется такая электрическая цепь, в которой ток от какого-либо источника может идти по различным путям и, в которой, следовательно, имеются точки, где сходятся два и более проводников. Эти точки называютузлами. Токи, текущие к узлу считаются имеющими один знак, а от узла – другой.
Учитывая это правило для схемы, изображенной на рис. 1.11,а можно записать


Для цепи, имеющей n ветвей, сходящихся в одном узле, имеем:

т.е. алгебраическая сумма токов ветвей, сходящихся в любом узле, равна
Рис. 1.11 Схема поясняющая законы Кирхгофа.
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа устанавливает связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре, который можно выделить в рассматриваемой цепи.
В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС, действующих в любом контуре разветвленной электрической цепи, равна алгебраической сумме падений напряжений на всех сопротивлениях контура

Рассмотрим электрическую цепь, изображенную на рис. 1.11,б. Обозначим стрелкой направление обхода контура. При составлении уравнений будем брать со знаком “плюс” те ЭДС и падения напряжений, направления которых совпадают с направлением обхода контура и со знаком “минус” те, которые направлены против обхода. Для цепи, изображенной на рис. 1.11,б второй закон Кирхгофа запишется в следующем виде:

Законы Ома и Кирхгофа в символической форме
В символической форме можно представить не только отдельные синусоидальные функции времени, но и уравнения, содержащие такие функций. Рассмотрим последовательную цепь с R, L, С. Мгновенные значения напряжения и тока для такой цепи связаны, на основании второго закона Кирхгофа, уравнением:
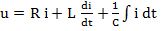
Пусть мгновенное значение тока в цепи определяется выражением
Полученным выражением соответствуют комплексные функции времени:
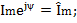
Напряжение на зажимах цепи является также синусоидальной функцией времени 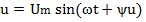
В соответствии с равенствам 4.5 мгновенные значения напряжений уравнения 4.7 представляют собой мнимые части соответствующих комплексных функций, взятые без множителя j:
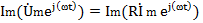
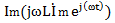
В данном случае при равенстве мнимых частей будут равны и действительные части комплексов напряжений, а следовательно равны и комплексные числа
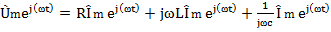
Разделим левую и правую части уравнения 4.8 на оператор вращения 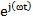
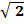
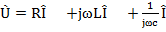
Сравнивая уравнения 4.7 и 4.9, можно сделать выводы:
а) для перехода от интегро-дифференциального уравнения к изображению в комплексной форме необходимо все мгновенные значения напряжений и токов заменить их комплексами; дифференцирование оригинала заменить умножением изображения на 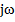
б) интетро-дифференциальному (или тригонометрическому) уравнению для мгновенных значений соответствует алгебраическое уравнение для изображений.
Таким образом, применение символического метода приводит к алгебраизации интегро-дифференциальных и тригонометрических уравнений, что позволяет применять для расчета цепей синусоидального тока все соотношения и законы цепей постоянного тока.
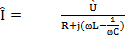
Полученное выражение представляет закон Ома в символической форме.
Величина, стоящая в знаменателе, называется комплексом полного сопротивления Z.
Комплекс полного сопротивления (или комплексное сопротивление) представляет собой комплексное число, действительная часть которого равна активному, а мнимая часть—реактивному сопротивлениям цепи.
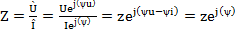
Модуль комплекса полного сопротивления равен полному сопротивлению цепи
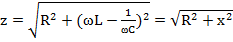
В выражении для комплекса полного сопротивления цепи
знак плюс перед мнимой частью ставится при индуктивном характере сопротивления ( 

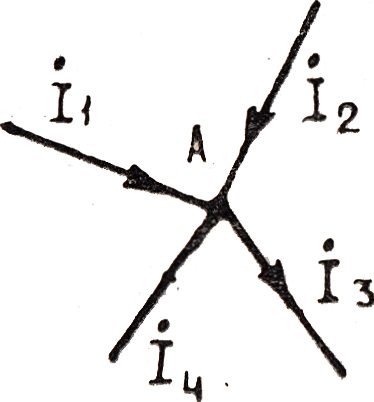
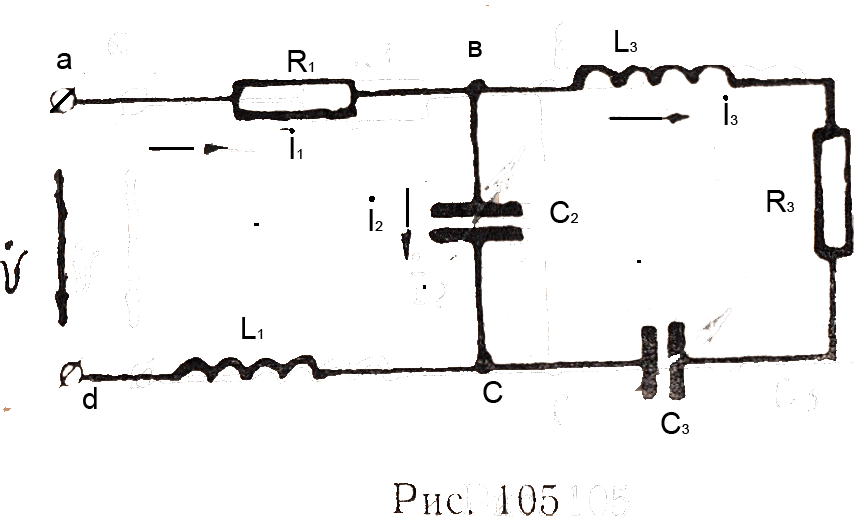
При изображении синусоидальных электрических величин в комплексной (символической) форме законы Кирхгофа имеют такой же вид, как и для цепей постоянного тока. Например, по первому закону Кирхгофа’ алгебраическая сумма комплексов токов, сходящихся в узле А (рис. 104), равна нулю, т.е. 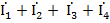
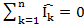
По второму закону Кирхгофа для замкнутого контура электрической цепи алгебраическая сумма комплексов э.д.с. действующих в контуре, равна алгебраической сумме комплексов падений, напряжений на отдельных участках этого контура. Так, для контура abed по второму закону Кирхгофа уравнение имеет вид:
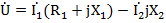
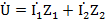
В общем виде уравнение по второму закону Кирхгофа записывается следующим образом:
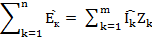
Пример 31. Определить ток в цепи если, активное сопротивление R = 80om,индуктивность L=90
мгн и конденсатор С = 35,5мкф, соединенные последовательно, включены в сеть с напряжением 220в и частотой 50гц.
Решение: Индуктивное сопротивление
Комплекс полного сопротивления цепи
Комплекс тока в цепи по закону Ома
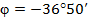
Решение. Индуктивное сопротивление
Комплекс полного сопротивления цепи
Полная комплексная проводимость катушки
Комплексная проводимость конденсатора
Полная комплексная проводимость всей цепи:
Ток в цепи (комплекс тока)
Характер сопротивления цепи активно-индуктивный, так как
Дата добавления: 2016-04-06 ; просмотров: 2811 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ