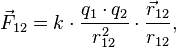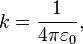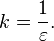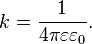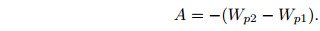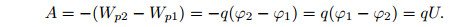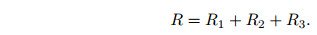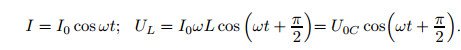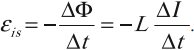закон кулона в дифференциальной форме
ВОПРОСЫ. 1. Закон Кулона. Теорема Гаусса в интегральной и дифференциальной формах
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14
1. Закон Кулона. Теорема Гаусса в интегральной и дифференциальной формах. Теорема о циркуляции для электростатического поля. Потенциал. Уравнение Пуассона.
Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами. Современная формулировка [1] :
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Важно отметить, что для того, чтобы закон был верен, необходимы:
Точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
Их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
Расположение зарядов в вакууме.
Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов. [2]
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
где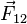 
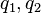
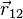
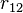
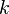
— сила, с которой заряд 1 действует на заряд 2; 
— величина зарядов; 
— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — 
); 
— коэффициент пропорциональности.
В СГСЭ единица измерения заряда выбрана таким образом, что коэффициент k равен единице.
В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c 2 ·10 −7 Гн/м = 8,9875517873681764·10 9 Н·м 2 /Кл 2 (или Ф −1 ·м). В СИ коэффициент k записывается в виде:
где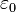 
≈ 8,85418781762·10 −12 Ф/м — электрическая постоянная.
В однородном изотропном веществе в знаменатель формулы добавляется диэлектрическая проницаемость среды ε.
Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния [1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).
В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.
Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
| СГС | СИ |
 |  |
— поток вектора напряжённости электрического поля через замкнутую поверхность 
.
— полный заряд, содержащийся в объёме, который ограничивает поверхность .
— электрическая постоянная.
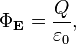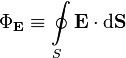
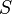
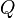
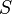
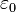
Данное выражение представляет собой теорему Гаусса в интегральной форме.
Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
В дифференциальной форме теорема Гаусса выражается следующим образом:
| СГС | СИ |
 |  |
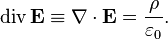Здесь 
— объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а 
— оператор набла.
Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана еще и иначе (альтернативным образом) — через поток вектораэлектрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
| СГС | СИ |
 |  |
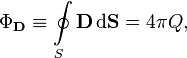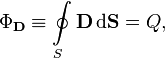Важный комментарий[показать]
В дифференциальной форме:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Закон Кулона
Поэтому, вычисляя дивергенцию поля () как производную произведения, получаем:
где введена следующая скалярная функция:
∫ δ a ( r ) d V = 3 a 2 4 π ∫ 0 ∞ ∫ 4 π r 2 d r d Ω ( r 2 + a 2 ) 5 / 2 = ∫ 0 ∞ 3 χ 2 d χ ( 1 + χ 2 ) 5 / 2 = χ 3 ( 1 + χ 2 ) 3 / 2 | 0 ∞ = 1. <\displaystyle \int \delta _(\mathbf 
Экспериментальным фактом является принцип суперпозиции:
поле, создаваемое несколькими зарядами, равно векторной сумме напряжённостей поля от каждого заряда.
Поэтому закон Кулона в дифференциальной форме может быть записан в следующем виде, который называют законом Гаусса:
то для ротора сферически симметричного поля получаем:
Поэтому как для закона Кулона, так и для его регуляризованного выражения () ротор будет равен нулю. В силу принципа суперпозиции это справедливо для любого статического распределения заряда. Поэтому уравнения электростатики имеют вид:
Последнее уравнение, выражающее центральный характер кулоновского поля для точечного заряда, выполняется автоматически, если:
Кулоновский потенциал поля точечного заряда равен
что проверяется вычислением его градиента () и сравнением с ().
Потенциал и напряжённость можно представить в интегральном виде, просуммировав кулоновские поля от зарядов малых объёмов:
d E d t = u F − q Q r 2 r u r = q Q r 3 ( r u ) − q Q r 3 ( r u ) = 0. <\displaystyle <\frac
При помощи теоремы Стокса равенство нулю ротора электрического поля можно записать в интегральном виде:
A = ∫ r 1 r 2 F d r = − ∫ r 1 r 2 q ∇ φ ( r ) d r = − q ∫ r 1 r 2 d φ = q φ ( r 1 ) − q φ ( r 2 ) <\displaystyle A=\int \limits _<\mathbf
равна разнице потенциалов в начальной и конечной точках (изменению потенциальной энергии) и поэтому не зависит от формы пути.
Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.
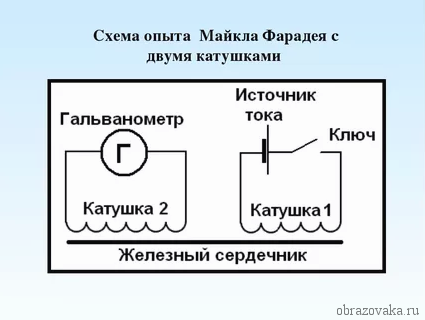
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Основные понятия и законы электростатики
Закон Кулона:
сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:
Коэффициент пропорциональности в этом законе
В СИ коэффициент k записывается в виде
где ε0 = 8, 85 · 10−12 Ф/м (электрическая постоянная).
Точечными зарядами называют такие заряды, расстояния между которыми гораздо больше их размеров.
Электрические заряды взаимодействуют между собой с помощью электрического поля. Для качественного описания электрического поля используется силовая характеристика, которая называется «напряжённостью электрического поля» (E). Напряжённость электрического поля равна отношению силы, действующей на пробный заряд, помещённый в некоторую точку поля, к величине этого заряда:
Направление вектора напряжённости совпадает с направлением силы, действующей на положительный пробный заряд. [E]=B/м. Из закона Кулона и определения напряжённости поля следует, что напряжённость поля точечного заряда
где q — заряд, создающий поле; r — расстояние от точки, где находится заряд, до точки, где создаётся поле.
Если электрическое поле создаётся не одним, а несколькими зарядами, то для нахождения напряжённости результирующего поля используется принцип суперпозиции электрических полей: напряжённость результирующего поля равна векторной сумме напряжённостей полей, созданных каждым из зарядов — источников в отдельности:
Работа электрического поля при перемещении заряда: найдём работу перемещения положительного заряда силами Кулона в однородном электрическом поле. Пусть поле перемещает заряд q из точки 1 в точку 2:
В электрическом поле работа не зависит от формы траектории, по которой перемещается заряд. Из механики известно, что если работа не зависит от формы траектории, то она равна изменению потенциальной энергии с противоположным знаком:
Отсюда следует, что
Потенциалом электрического поля называют отношение потенциальной энергии заряда в поле к этому заряду:
Запишем работу поля в виде
Здесь U = ϕ1 − ϕ2 — разность потенциалов в начальной и конечной точках траектории. Разность потенциалов называют также напряжением
Часто наряду с понятием «разность потенциалов» вводят понятие «потенциал некоторой точки поля». Под потенциалом точки подразумевают разность потенциалов между данной точкой и некоторой заранее выбранной точкой поля. Эту точку можно выбирать в бесконечности, тогда говорят о потенциале относительной бесконечности.
Потенциал поля точечного заряда подсчитывается по формуле
Проекция напряжённости электрического поля на какую-нибудь ось и потенциал связаны соотношением
Электроёмкость. Конденсаторы. Энергия электрического поля
Электроёмкостью тела называют величину отношения
Формула для подсчёта ёмкости плоского конденсатора имеет вид:
где S — площадь обкладок, d — расстояние между ними.
Конденсаторы можно соединять в батареи. При параллельном соединении ёмкость батареи C равна сумме ёмкостей конденсаторов:
Разности потенциалов между обкладками одинаковы, а заряды прямо пропорциональны ёмкостям.
При последовательном соединении величина, обратная ёмкости батареи, равна сумме обратных ёмкостей, входящих в батарею:
Заряды на конденсаторах одинаковы, а разности потенциалов обратно пропорциональны ёмкостям.
Заряженный конденсатор обладает энергией. Энергию заряженного конденсатора можно подсчитать по любой из следующих формул:
Основные понятия и законы постоянного тока
Электрический ток — направленное движение электрических зарядов. В разных веществах носителями заряда выступают элементарные частицы разного знака. За положительное направление тока принято направление движения положительных зарядов. Количественно электрический ток характеризуют его силой. Это заряд, прошедший за единицу времени через поперечное сечение проводника:
Закон Ома для участка цепи имеет вид:
Коэффициент пропорциональности R, называемый электрическим сопротивлением, является характеристикой проводника [R]=Ом. Сопротивление проводника зависит от его геометрии и свойств материала:
где l — длина проводника, ρ — удельное сопротивление, S — площадь поперечного сечения. ρ является характеристикой материала и его состояния. [ρ] = Ом·м.
Проводники можно соединять последовательно. Сопротивление такого соединения находится как сумма сопротивлений:
При параллельном соединении величина, обратная сопротивлению, равна сумме обратных сопротивлений:
Для того чтобы в цепи длительное время протекал электрический ток, в составе цепи должны содержаться источники тока. Количественно источники тока характеризуют их электродвижущей силой (ЭДС). Это отношение работы, которую совершают сторонние силы при переносе электрических зарядов по замкнутой цепи, к величине перенесённого заряда:
Если к зажимам источника тока подключить нагрузочное сопротивление R, то в получившейся замкнутой цепи потечёт ток, силу которого можно подсчитать по формуле
Это соотношение называют законом Ома для полной цепи.
Электрический ток, пробегая по проводникам, нагревает их, совершая при этом работу
где t — время, I — сила тока, U — разность потенциалов, q — прошедший заряд.
Закон Джоуля-Ленца:
Основные понятия и законы магнитостатики
Основные понятия и законы электромагнитной индукции
Если замкнутый проводящий контур пронизывается меняющимся магнитным потоком, то в этом контуре возникает ЭДС и электрический ток. Эту ЭДС называют ЭДС электромагнитной индукции, а ток — индукционным. Явление их возникновения называют электромагнитной индукцией. ЭДС индукции можно подсчитать по основному закону электромагнитной индукции или по закону Фарадея:
Знак «−» связан с направлением индукционного тока. Оно определяется по правилу Ленца:
индукционный ток имеет такое направление, что его действие противодействует причине, вызвавшей появление этого тока.
Магнитный поток, пронизывающий контур, прямо пропорционален току, протекающему в этом контуре:
Коэффициент пропорциональности L зависит от геометрии контура и называется индуктивностью, или коэффициентом самоиндукции этого контура. [L] = 1 Гн
Энергию магнитного поля тока можно подсчитать по формуле
где L — индуктивность проводника, создающего поле; I — ток, текущий по этому проводнику
Электромагнитные колебания и волны
Колебательным контуром называется электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью C и катушки с индуктивностью L (см. рис. 7).
Для свободных незатухающих колебаний в контуре циклическая частота определяется формулой
Период свободных колебаний в контуре определяется формулой Томсона:
Если в LC-контур последовательно с L, C и R включить источник переменного напряжения, то в цепи возникнут вынужденные электрические колебания. Такие колебания принято называть переменным электрическим током
В цепь переменного тока можно включать три вида нагрузки — конденсатор, резистор и катушку индуктивности.
Конденсатор оказывает переменному току сопротивление, которое можно посчитать по формуле
Ток, текущий через конденсатор, по фазе опережает напряжение на π/2 или на четверть периода, а напряжение отстаёт от тока на такой же фазовый угол.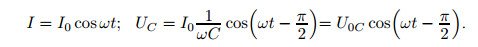
Катушка индуктивности оказывает переменному току сопротивление, которое можно посчитать по формуле
Ток, текущий через катушку индуктивности, по фазе отстаёт от напряжения на π/2 или на четверть периода. Напряжение опережает ток на такой же фазовый угол.
Трансформатором называется устройство, предназначенное для преобразования переменных токов. Трансформатор состоит из замкнутого стального сердечника, на который надеты две катушки. Катушка, которая подключается к источнику переменного напряжения, называется первичной обмоткой, а катушка, которая подключается к потребителю, называется вторичной обмоткой. Отношение напряжения на первичной обмотке и вторичной обмотке трансформатора равно отношению числа витков в этих обмотках:
Если K > 1, трансформатор понижающий, если K 
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
Рис. 3. Возникновение вихревого магнитного поля
Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.
Что мы узнали?
Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
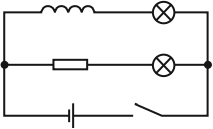
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
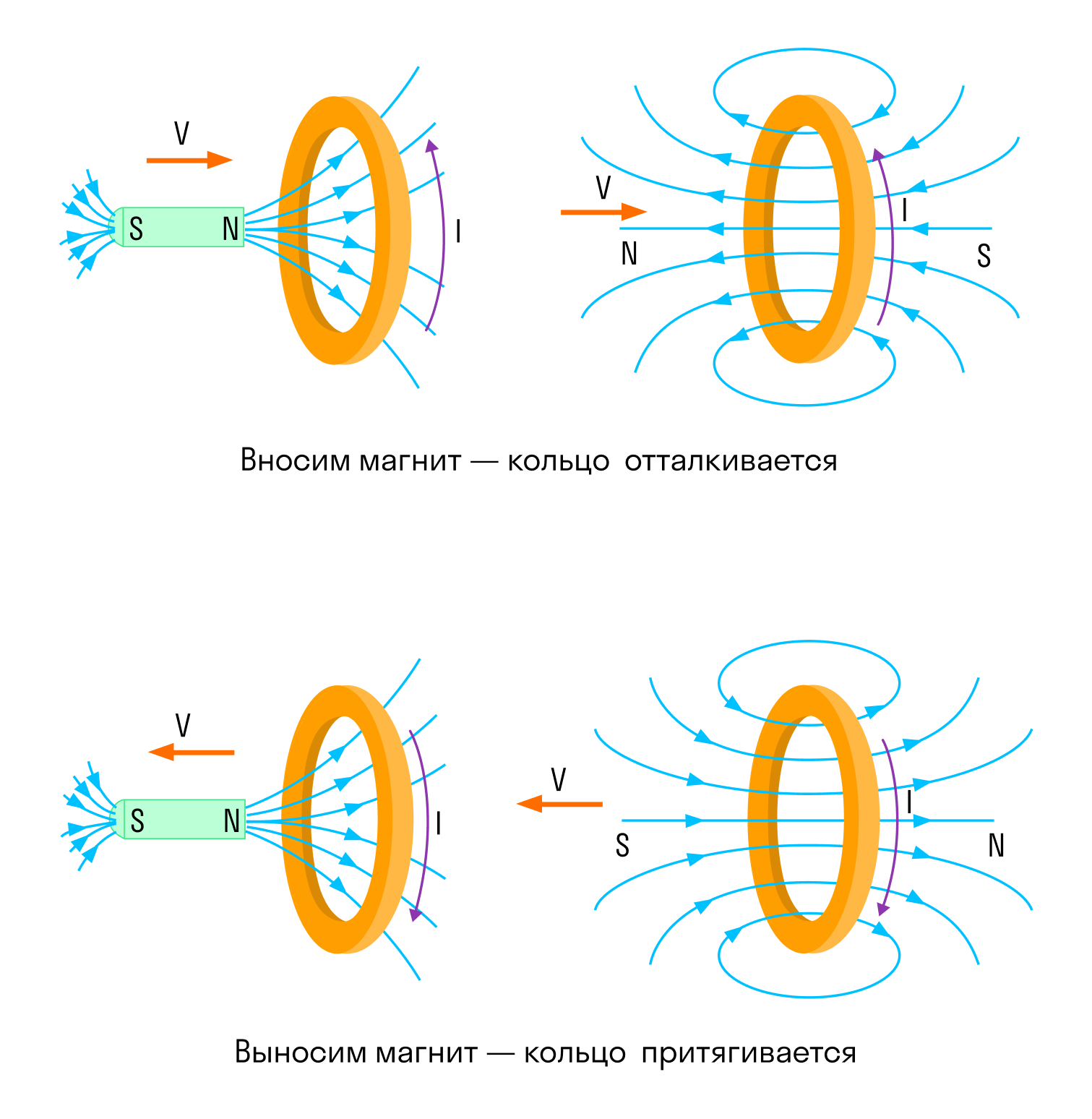
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Задачи на применение закона Фарадея
Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный Φ1 и уменьшающийся после этого до 0. Найдите величину заряда, проходящего по цепи.
Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:
Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:
Полное сопротивление цепи здесь обозначено буквой R.
Для нахождения заряда, идущего по цепи, нам пригодится выражение:
Поставим эти выражения в нужную формулу и получим:
Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.
Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна l. Она движется поступательно с постоянной скоростью v в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию εi от расстояния x.
Найти ответ можно с помощью закона Фарадея.
Для получения искомой функции Ei(x) нам нужно построить функцию Ф(x). Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:
Расстояние до точки рассмотрения здесь обозначено буквой r.
Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:
С учетом приведенных выше выражений, а также того факта, что B→⊥S→, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:
Далее вычисляем величину полного потока, учитывая, что x≤r≤x+a:
После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее: