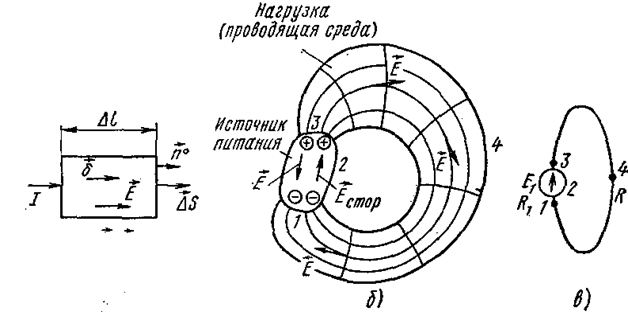
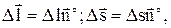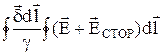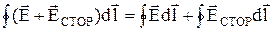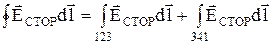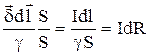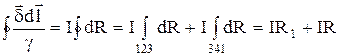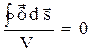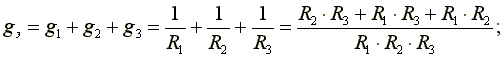закон ома и кирхгофа в дифференциальной форме

ЗАКОНЫ оМА И КИРХГОФА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

Выделим в проводящей среде небольшой параллелепипед объемом ΔV. Длина ребра параллелепипеда Δl, площадь поперечного сечения Δs. Расположим этот параллелепипед так, чтобы напряженность поля в нем была направлена параллельно ребру (рис. 1, а). В силу малости объема можно считать, что напряженность электрического поля 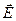одна и та же во всем элементарном объеме:

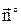
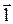
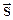
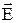
где — единичный вектор по направлению Δ, Δи .

Ток.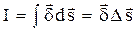

Напряжение на элементе объема .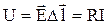

Сопротивление элемента объема .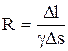

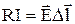
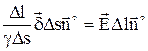
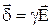
Подставив в выражение эквиваленты R и I, получим

,

. (1)

Соотношение (1) называют законом Ома в дифференциальной форме. Оно устанавливает связь между плотностью тока в данной точке проводящей среды и напряженностью поля в этой же точке.

Уравнение (1) справедливо для областей вне источников э. д. с. В областях, занятых источниками э. д. с., кроме кулонова (электростатического) поля, существует еще так называемое стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи.

Под сторонним электрическим полем понимают электрическое поле не электростатической природы (например, обусловленное химическими, электрохимическими, тепловыми, термоэлектрическими, механическими или электромагнитными процессами).

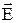
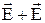
Напряженность стороннего поля обозначают _стор. В областях, занятых источниками э. д. с., полное значение напряженности поля равно геометрической сумме напряженности кулонова и стороннего полей _стор.

На рис. 3.1, б схематически изображена электрическая цепь постоянного тока. Она состоит из источника питания и нагрузки.

Источник сторонней э. д. с. создает внутри источника питания стороннюю напряженность поля 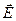_стор.

Линейный интеграл от сторонней напряженности поля внутри источника называется э. д. с. источника (Е₁):

(2)

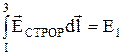
Под действием стороннего поля в источнике непрерывно происходит разделение электрических зарядов. Положительные заряды перемещаются к плюсу источника, а отрицательные — к минусу.

Эти заряды в области внутри и вне источника создают электрическое поле, напряженность которого, как и напряженность электростатического (кулонова) поля, направлена от положительных зарядов к отрицательным.

При протекании постоянного тока по цепи одни электрические заряды непрерывно сменяются другими, такими же, как и в предыдущие моменты времени. Таким образом, картина поля в макроскопическом смысле повторяется в смежные моменты времени. Поле носит как бы статический характер. Это и послужило основанием для того, чтобы поле, созданное в проводящей среде разделившимися зарядами, называть кулоновым полем, а его напряженность Е называть напряженностью кулонова поля.

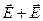
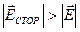
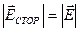
Внутри источника кулоново поле направлено навстречу стороннему полю. Полное значение напряженности поля внутри источника равно _стор. Вне источника кулоново поле направлено от положительного электрода к отрицательному. Под действием этого поля и происходит упорядоченное движение зарядов в области вне источника. При протекании тока по цепи . При разомкнутой цепи .

Закон Ома в дифференциальной форме для областей, занятых источниками э. д. с., записывают следующим образом:

. (3)

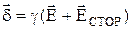
Уравнение (3) в литературе называют обобщенным законом Ома в дифференциальной форме.

Если от обеих частей уравнения (3) взять интеграл по замкнутому контуру, включающему в себя источник э. д. с., то из уравнения (3) будет получен второй закон Кирхгофа. Поэтому уравнение (3) называют также вторым законом Кирхгофа в дифференциальной форме.

На рис. 1, в изображен замкнутый контур, по которому течет ток I. На участке 123 имеется источник сторонней э. д. с. Е₁. На участке 341 нет источников сторонней э. д. с. Обозначим через R₁ сопротивление участка 123 и через R — сопротивление участка 341. Примем, что площадь поперечного сечения всех участков замкнутого контура достаточно мала для того, чтобы можно было считать направление плотности тока и направление напряженности поля в некоторой точке совпадающими с направлением элемента пути 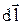в той же точке.

Умножим обе части (3) на 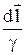и составим циркуляцию вдоль замкнутого контура 12341 рис. 1, в:

Интеграл от суммы равен сумме интегралов. Поэтому

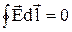
в силу потенциально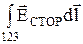го характера кулонова поля.

но равен сторонней э. д. с.E₁, a, так как на участке 341 нет сторонней э. д.с.

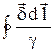
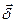
Для подсчета величины умножим и разделим подынтегральное выражение на площадь поперечного сечения S, от плотности тока перейдем к току I и заменим на сопротивление участка пути dR. Получим:

Таким образом, из уравнения (3) образовано уравнение

составленное по второму закону Кирхгофа.

Первый закон Кирхгофа в дифференциальной форме

Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, который войдет в объем, должен равняться току, вышедшему из объема, иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Сумму входящего в объем и выходящего из объема токов записывают так:

(4)

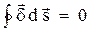
Если разделить и левую и правую части (2) на одно и то же число (на объем, о котором шла речь), то равенство останется справедливым:

Очевидно, что последнее соотношение будет справедливо и в том случае, если объем, находящийся внутри замкнутой поверхности, будет стремиться к нулю:

Таким образом, для постоянного, неизменного во времени поля в проводящей среде

(5)

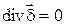
Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме (при постоянном токе) в любой точке поля нет ни истока, ни стока линий тока проводимости .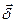

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.

Первый закон Кирхгофа является следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через эту поверхность должно быть равно количеству входящих зарядов.

Обобщая сказанное на произвольное число ветвей сходящихся в узле, можно сформулировать первый закон Кирхгофа следующим образом:

в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов.

Второй закон Кирхгофа связан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру, то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.

Сформулируем оба варианта второго закона Кирхгофа, т.к. они принципиально равноценны:

знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;

знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.

Для линейного элемента справедливо

Закон Джоуля-Ленца. Если по активному сопротивлению (проводнику) течет постоянный ток, то работа тока на этом участке идет на преобразование электрической энергии во внутреннюю. Увеличение внутренней энергии проводника приводит к повышению его температуры (проводник нагревается).

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

Математически может быть выражен в следующей форме:

где w — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах [3] :

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

В математической форме этот закон имеет вид

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂. В случае постоянных силы тока и сопротивления:

3.Анализ электрического состояния цепей постоянного тока В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы.

После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи

Ток I1 в неразветвленной части схемы определяется по формуле:

Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:

Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:

В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Пример параллельной цепи является — ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.

Все те, кто знаком с основами электротехники, представляют себе значение закона Ома в теории и практике электрических цепей. Не вдаваясь в подробности, перечислим некоторые примеры использования закона Ома при изучении электрических цепей.

В первую очередь, как уже упоминалось, закон Ома в виде

служит для определения сопротивления проводника. При наличии амперметра и вольтметра эта операция даже для неопытного экспериментатора не представит трудностей. Одним из наиболее точных и чувствительных способов определения сопротивления является метод мостовых схем, расчет которых производится также с использованием закона Ома.

Применяя закон Ома для полной цепи, можно, изменяя внешнее сопротивление, вычислить ЭДС и внутреннее сопротивление источника тока, решив для этого систему двух соответствующих выражений:

ПоказанияI₁ и I₂ при этом снимают с амперметра, включенного в цепь. Сопротивление R₁ и R₂ внешних участков цепи можно найти, измеряя вольтметром падение напряжения на этих участках и применяя формулу закона Ома для участка цепи.

Этот же закон позволяет рассчитать электрическую цепь, источником тока в которой является батарея, составленная из нескольких элементов.

В настоящее время в электротехнике широко применяются правила Кирхгофа, с помощью которых рассчитывают разветвленные цепи. Зная эти правила, можно, например, определить силу и направление тока в любой части разветвленной системы проводников, если заданы сопротивления и ЭДС всех его участков. Второе правило Кирхгофа получено в результате применения закона Ома к различным участкам замкнутой цепи. Первое правило также следует из теоретических рассуждений Ома, изложенных им в работе «Теоретические исследования электрических цепей».

Изучение нелинейных цепей обязано своим прогрессом также закону Ома. Важнейшие характеристики электронных ламп и полупроводниковых приборов — крутизна характеристики, внутреннее сопротивление — определяется в соответствии с законом Ома.

Закон Ома применяется ко всей цепи. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа

Последовательное соединение элементов
электрических цепей

На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.

Рис. 2.1

Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи. где — эквивалентное сопротивление.

Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.

Параллельное соединение элементов
электрических цепей

На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.

Рис. 2.2

Токи в параллельных ветвях определяются по формулам:

где — проводимости 1-й, 2-й и n-й ветвей.

В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.

где

Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости

Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость

Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента

Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.

Рис. 2.3 Эквивалентная проводимость схемы

,

а эквивалентное сопротивление Напряжение на входе схемы Токи в параллельных ветвях

Аналогично

Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.

Преобразование треугольника сопротивлений
в эквивалентную звезду

Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.

Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

Эквивалентное соединение полученной схемы определяется по формуле

Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.

Преобразование звезды сопротивлений
в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.

2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:

Эквивалентное сопротивление преобразованной схемы равно

При решении схемы методом непосредственного преобразования элементов используют серию эквивалентных преобразований схемы, направленных на упрощение схемы. Понятие эквивалентного преобразования подразумевает такое изменение состава и/или топологии фрагментасхемы, при котором не изменяются электрические показатели (токи и напряжения) в остальных частях схемы, не затронутых преобразованием. Такое обстоятельство означает, что величины, найденные для одной из эквивалентных схем (искомые или вспомогательные), действительны и для любой другой из эквивалентных схем.

Источник