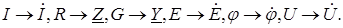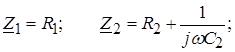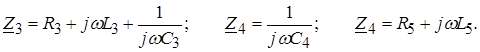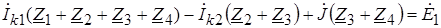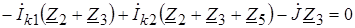закон ома закон кирхгофа в комплексной форме

Законы Ома и Кирхгофа в комплексной форме

Выражениязакона Ома в комплексной форме имеют вид

(4.14)

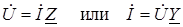
Первый закон Кирхгофа для мгновенных значений токов, имеющий вид

,

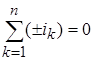
в комплексной форме записываются в виде

,

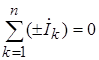
т.е. алгебраическая сумма комплексных токов ветвей в любом узле ЭЦ равна нулю.

, (4.16)

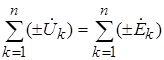
т.е. алгебраическая сумма комплексных напряжений в любом замкнутом контуре ЭЦ равна алгебраической сумме комплексных ЭДС в том же контуре.

Вывод: законы Ома и Кирхгофа, записанные в комплексной форме, имеют такой же вид, что и для цепей постоянного тока. Поэтому для расчета цепей синусоидального тока символическим методом применимы все методы расчета резистивных цепей, если в них произвести замены

Расчет ЭЦ символическим методом производится в следующем порядке:

1) от заданных гармонических воздействий переходят к комплексным изображениям;

2) с помощью любого известного метода расчета определяют комплексные токи и напряжения (реакция цепи);

3) от комплексных изображений токов и напряжений переходят к их мгновенным значениям.

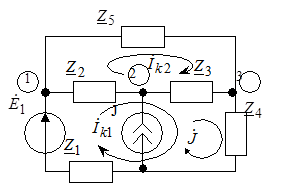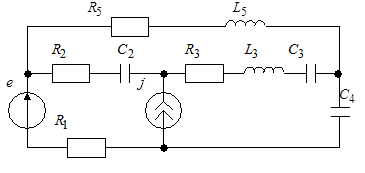
Пример: Составить уравнения по МКТ и МУН для схемы рис. 4.3.

;

;

Метод контурных токов (МКТ)

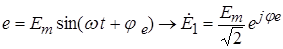
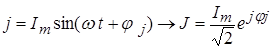
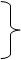
I.

II.

Метод узловых напряжений (МУН)

1) ;

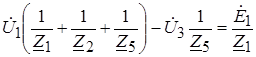
2) ;

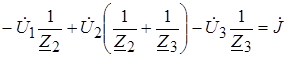
3) .

Источник

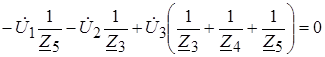
Законы Ома и Кирхгофа в комплексной форме

Выражения закона Ома в комплексной форме имеют вид:

(2.12)

(2.13)

(2.14)

(2.15)

Достоинство этих выражений заключается в том, что в них учитывается как связь между действующими током и напряжением , так и сдвиг фаз φ между ними.

Первый закон Кирхгофав применении к узлу цепи, для мгновенных токов имеющий вид , в комплексной форме записывается в виде

(2.16)

т.е. сумма комплексных токов, направленных к узлу, равна сумме комплексных токов, направленных от него, т.е. алгебраическая сумма комплексных токов в узле равна 0.

Второй закон Кирхгофав применении к контуру цепи, для мгновенных ЭДС и падений напряжений имеющий вид , в комплексной форме записывается в виде

(2.17)

где — комплексные ЭДС, падение напряжения, ток и сопротивление в k-й ветви, входящей в контур.

Для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений.

Если в ветвь входят последовательно соединенные участок с сопротивлением r_k, катушка с индуктивностью L_k и конденсатор с емкостью C_k, то

или

для этой ветви имеем:

Как было указано выше, необходимо перед составлением уравнений по законам Кирхгофа задать положительные направления ЭДС, токов и напряжений во всех ветвях цепи, обозначив эти направления на схеме стрелками. В этом отношении полезным может оказаться обозначение ЭДС, токов и напряжений двойными индексами, соответствующими обозначению узлов, между которыми находится данная ветвь цепи. Достаточно условиться, что положительное направление принимается от узла, соответствующего первому индексу, к узлу, соответствующему второму индексу, и тогда уже нет необходимости ставить стрелки на схеме, а сама аналитическая запись величин указывает принятое их положительное направление. При изменении порядка расположения индексов меняется знак ЭДС, тока или напряжения. Так как сопротивления ветвей цепи и проводимости являются параметрами, не имеющими направления, то порядок индексов у них безразличен.

Все эти правила действуют и при использовании комплексного метода, т.е. имеют место соотношения:

Источник

Закон ома закон кирхгофа в комплексной форме

Задача анализа установившегося режима в ЭЦ синусоидального тока

Среди режимов работы ЭЦ различают установившиеся и переходные режимы. Установившиеся режимы имеют место в результате сколь угодно длительного воздействия источников энергии в ЭЦ. В ЭЦ с источниками постоянного напряжения и тока токи ветвей и напряжения на них неизменны во времени. В ЭЦ с источниками периодических напряжений и токов (синусоидальных и несинусоидальных) токи в ветвях и напряжения на них являются периодическими функциями времени.

Решение задачи анализа установившегося режима в ЭЦ с источниками синусоидального напряжения и тока во временной области сводится к отысканию частного решения системы дифференциальных уравнений, записанных по законам Кирхгофа для контуров и узлов ЭЦ. Но такой расчет для цепей с числом независимых контуров более двух связан с громоздкими выкладками, вызванными тем, что искомые начальные фазы токов находятся под знаком тригонометрических функций.

Комплексные амплитуды и комплексы

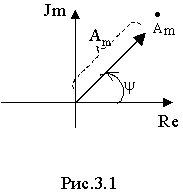
При расчете этим методом всякой синусоидальной функции времени

A m Sin ( w t+ y ) ставится в соответствие комплексное число вида

Во многих случаях пользуются понятием комплекса синусоидальной величины

т.е. комплексного числа с модулем в виде действующего значения синусоидальной величины и аргументом в виде начальной фазы.

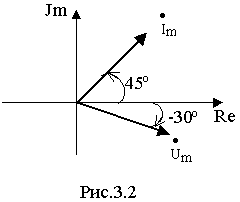
Существует взаимно-однозначное соответствие между комплексной амплитудой и синусоидальной функцией времени. Например, мгновен-ныму значению напряжения u=25Sin(314t-30 o )B соответствует комплекс-ная амплитуда 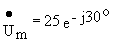B и вектор на комплексной плоскости (рис.3.2).

Примечание. Естественно, что масштабные коэффициенты при построении векторов тока и напряжения на комплексной плоскости могут быть разными.

Комплексное сопротивление и комплексная проводимость

Отношение комплексной амплитуды напряжения на зажимах двухполюсника к комплексной амплитуде тока, протекающего через эти зажимы, называется комплексным сопротивлением пассивного двухпо-люсника

Ом.

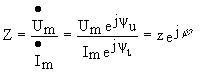
Модуль комплексного сопротивления, равный отношению амплитуды напряжения к амплитуде тока называется полным сопротивлением двухполюсника, т.е.

Аргументом комплексного сопротивления является фазовый сдвиг между напряжением и током на зажимах двуполюсника, т.е.

Представляя комплексное сопротивление, как комплексное число, в алгебраической форме, получим

Z=z Cos j +j z Sin j = 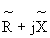(Ом)

Вещественная и мнимая части комплексного сопротивления двухполюсника носят название соответственно активной и реактивной составляющих комплексного сопротивления.

Величина обратная комплексному сопротивлению называется комплексной проводимостью

Сим

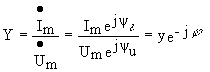
Модуль комплексной проводимости, равный отношению амплитуды тока к амплитуде напряжения называется полной проводимостью двухполюсника, т.е.

Аргументом комплексной проводимости является фазовый сдвиг между напряжением и током на зажимах двуполюсника, взятый со знаком (-)

Представляя комплексную проводимость, как комплексное число, в алгебраической форме, получим

Вещественная и мнимая части комплексной проводимости двухполюсника носят название соответственно активной и реактивной составляющих комплексной проводимости.

Законы Ома и Кирхгофа в комплексной форме

Введение понятий комплексного сопротивления и комплексной проводимости означает, по-существу, введение закона Ома в комплексной форме для установившегося синусоидального режима

или .

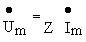
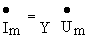
Комплексная амплитуда напряжения на зажимах пассивного двухполюсника равна комплексной амплитуде тока, умноженной на комплексное сопротивление двухполюсника.

Пример 1. Через зажимы двухполюсника с комплексным сопротивлением Z=40e j30 Ом протекает синусоидальный ток i =3 Sin (314 t + 15 o ) A. Определить напряжение u(t) на зажимах двухпо-люсника.

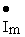
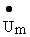
Находя комплексную амплитуду тока =3е j15 и зная комплексное сопротивление двухполюсника, на основании закона Ома в комплексной форме определяем комплексную амплитуду напряжения

=3е j15 ґ 40e j30 =120 е j45 В.

Следовательно, мгновенное напряжение равно u=120 Sin (31 4 t + 45 o ), B.

Первый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.

.

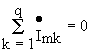
Поскольку каждое слагаемое в представленном выражении есть вектор, то результат есть сумма векторов. Это обстоятельсво позволяет контролировать аналитические расчеты наглядными графическими построениями-векторными диаграммами.

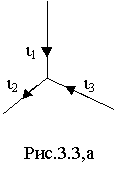
Пример 2 В узле ЭЦ сходятся 3 ветви с синусоидальными токам одной частоты (рис.3.3,а).

Решение. На основании первого закона Кирхгофа в комплексной форме находим

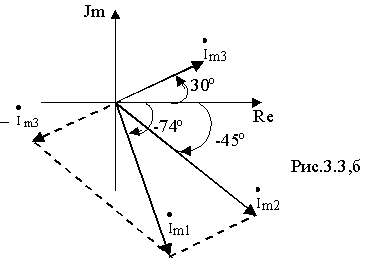
Построив вектора токов на комплексной плоскости (рис.3.3,б), убеждаемся, что сумма их действительно равна 0.

Переходя от комплекса к мгновенному значению, получим i 1 = 101 Sin( 100t-74 o ), А.

Второй закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом

.

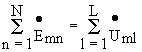
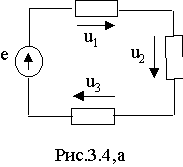
Пример 3. Известны мгновенные значения напряжений на элемен-тах контура ( рис.3.4,а) u 1 = 10 Sin( 100t-45 o ) B, u 2 = 25 Sin( 100t+30 o )B, u 3 = 5 Sin( 100t+60 o )B. Требуется определить мгновенное значение ЭДС источника напряжения.

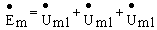
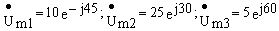
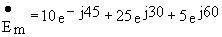
Переходя к комплексам, получим , где

.

=

=30.75+j9.75= 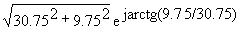@ 32.3e j18 в.

Построив вектора напряжений на комплексной плоскости (рис.3.4,б ) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e= 32.3 Sin( 100t+18 o ), В.

Источник

Законы Ома и Кирхгофа в комплексной форме.

Введение понятий комплексного сопротивления и комплексной проводимости означает, по-существу, введение закона Ома в комплексной форме для установившегося синусоидального режима

или.

Комплексная амплитуда напряжения на зажимах пассивного двухполюсника равна комплексной амплитуде тока, умноженной на комплексное сопротивление двухполюсника.

Пример 1. Через зажимы двухполюсника с комплексным сопротивлением Z=40e j30 Ом протекает синусоидальный ток i =3 Sin (314 t + 15 o ) A. Определить напряжение u(t) на зажимах двухполюсника.

Находя комплексную амплитуду тока и зная комплексное сопротивление двухполюсника, на основании закона Ома в комплексной форме определяем комплексную амплитуду напряжения

Следовательно, мгновенное напряжение равно u=120 Sin (314 t + 45 o ), B.

Первый закон Кирхгофа в комплексной форме: Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.

.

Пример 2. В узле электрической цепи сходятся 3 ветви с синусоидальными токам одной частоты (рис.3.3,а).

Мгновенные значения токов i ₂ и i ₃ определяются выражениями i₂= 100 Sin( 100t-45 o ) и i₃= 50 Sin( 100t+30 o ). Требуется определить ток i₁, пользуясь методом комплексных амплитуд.

На основании первого закона Кирхгофа в комплексной форме находим

, где ,

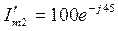
Построив вектора токов на комплексной плоскости (рис.3.3,б), убеждаемся, что сумма их действительно равна 0.

Переходя от комплекса к мгновенному значению, получим i₁= 101 Sin(100t-74 o ), А.

.

Пример 3. Известны мгновенные значения напряжений на элемен-тах контура ( рис.3.4,а) u₁= 10 Sin( 100t-45 o ) B, u₂= 25 Sin( 100t+30 o )B, u₃= 5 Sin( 100t+60 o )B. Требуется определить мгновенное значение ЭДС источника напряжения.

На основании второго закона Кирхгофа для мгновенных значений напряжений и ЭДС находим e = u₁+ u₂+ u₃.

Переходя к комплексам, получим

, где

; ;

=

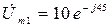
Построив вектора напряжений на комплексной плоскости (рис.3.4,б) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e = 32.3 Sin(100t+18 o ), В.

Метод комплексных амплитуд.

Метод комплексных амплитуд — метод расчета линейных радиотехнических цепей, содержащих реактивные элементы, в установившемся режиме при гармонических входных сигналах.

Суть метода заключается в следующем:

1) Для всех реактивных элементов определяется их комплексный импеданс.

2) Все токи и напряжения рассматриваются в виде комплексных амплитуд.

После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе:

— импедансы трактуются как обычные сопротивления;

— комплексные амплитуды токов и напряжений как обычные токи и напряжения.

Таким образом, мы избавились от реактивности элементов и зависимости от времени сигналов. Эти факторы, затрудняющие математические операции при описании схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными.

Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.

Данный метод применяется для расчёта разветвлённых цепей переменного тока, содержащих реактивные сопротивления (конденсаторы и индуктивности). Сопротивления

этих элементов записываются через комплексные числа.

Сопротивление конденсатора будет равно: Z_c=j/ωC,

сопротивление индуктивности: Z_L=jωL,

где j – мнимая единица вместо i, так как через i обозначается ток,

ω – циклическая частота, которая равна 2πν,

C и L – соответственно ёмкость и индуктивность.

Если последовательно резистору включён конденсатор, то их общее сопротивление записывается, как R-jZ_c, если индуктивность, то общее сопротивление равно R+jZ_L.

1) Закон Ома для участка цепи содержащего ЭДС:

φ1 φ2

φ1 – узел, от которого течёт ток;

φ2– узел, к которому течёт ток;

V1 – источник, включённый по направлению тока;

V2– источник, включённый противоположно направлению тока;

R1 – сопротивление ветви.

2) Закон сохранения заряд:

Далее решая эту систему, получим комплексные значения токов в ветвях. Чтобы получить значения токов, которые будут показывать амперметры, нужно просто взять модули этих комплексных токов.

Пример:

Рассчитаем методом комплексных амплитуд с помощью правил Кирхгофа данную цепь.

Источник