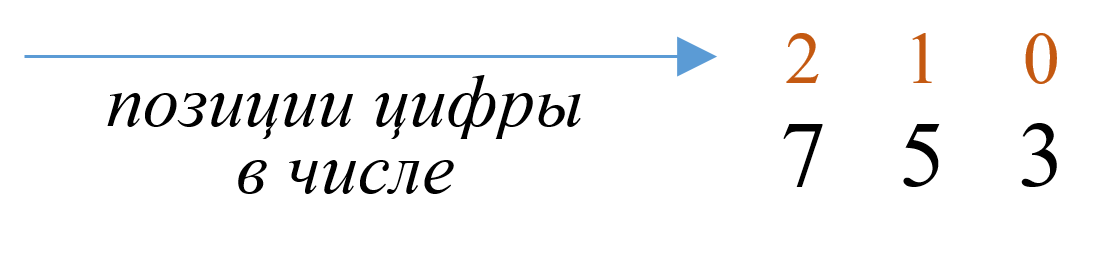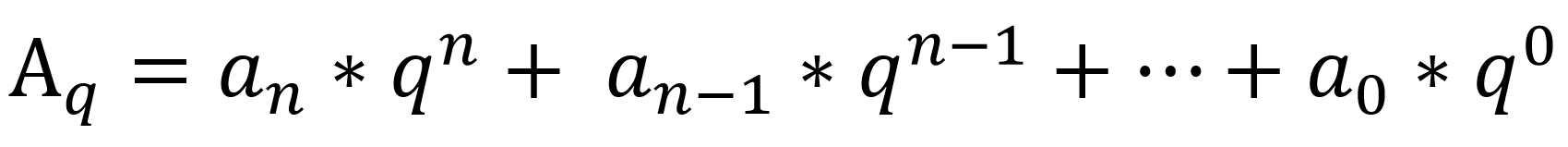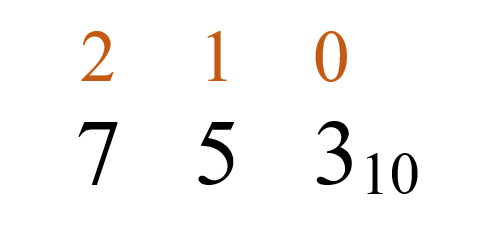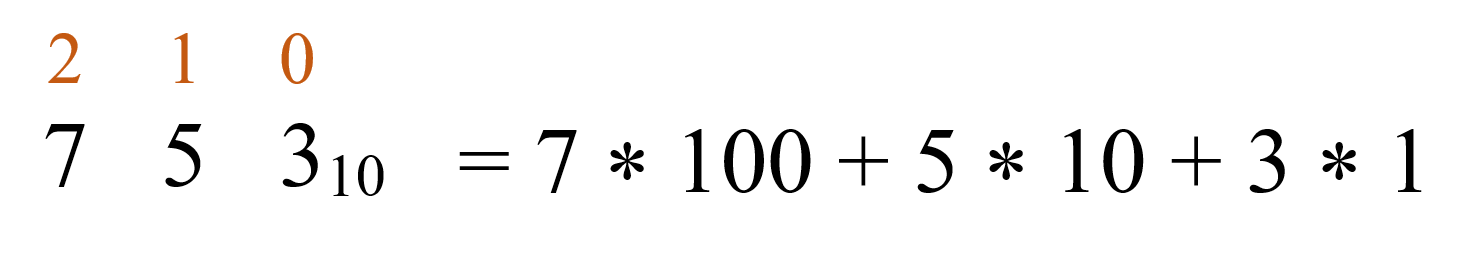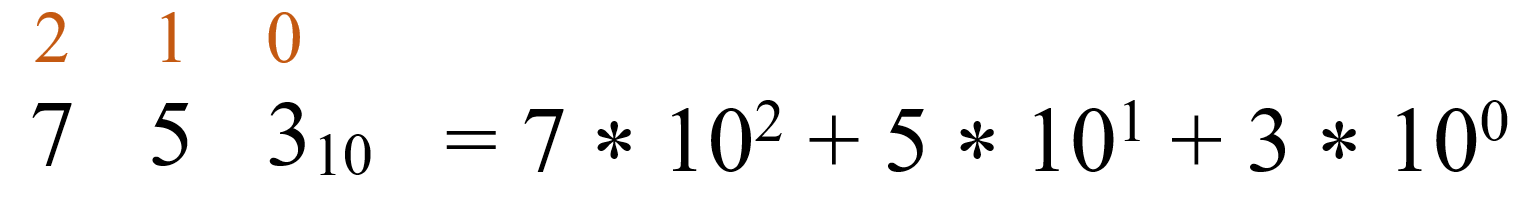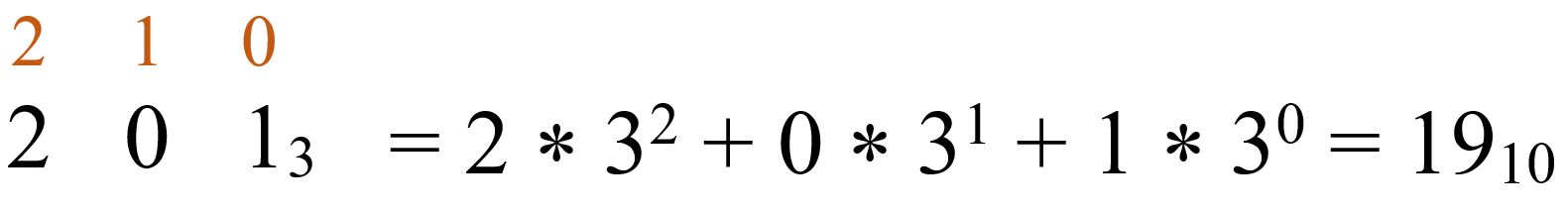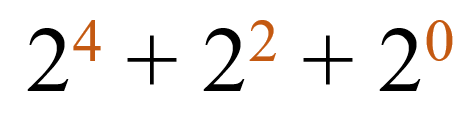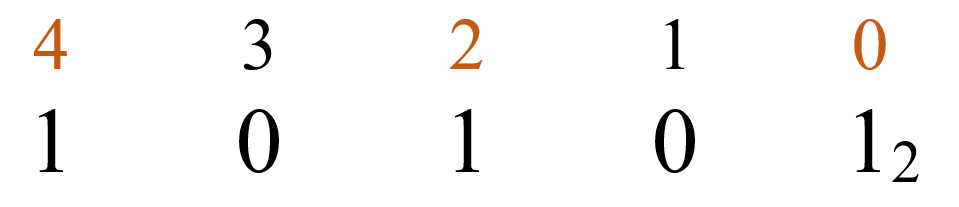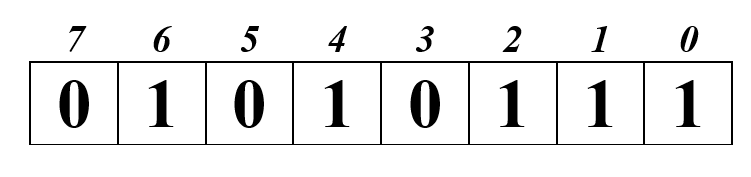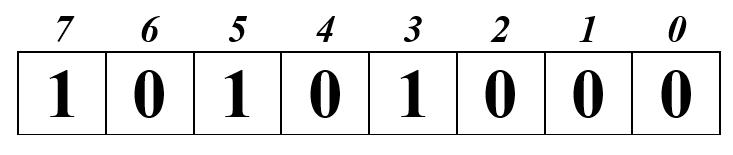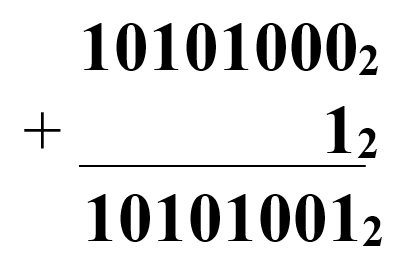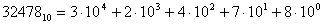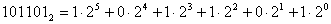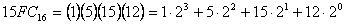записать десятичные числа в развернутой форме

20.03.202303.04.2023 admin 0 Комментариев

Перевод чисел из одной системы счисления в другую

Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.

Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.

Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
200₁₀ = 11001000₂ = 310₈ = C8₁₆

Кратко об основных системах счисления

Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.

Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.

Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.

Перевод в десятичную систему счисления

Перевод из десятичной системы счисления в другие

Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.

Переведем число 375₁₀ в восьмеричную систему:

Перевод из двоичной системы в восьмеричную

Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:

Перевод из двоичной системы в шестнадцатеричную

Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:

Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Перевод из восьмеричной системы в двоичную

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Используем таблицу триад:

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

Перевод из шестнадцатеричной системы в двоичную

Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.

Используем таблицу тетрад:

Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.

Перевод из восьмеричной системы в шестнадцатеричную и наоборот

Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме

Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?

Ответ

Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

Переход от свернутой формы к развернутой

1. Посмотрите на данное вам число и определите количество его цифр.

Пример:
Напишите 5827 в развернутом виде.

Прочитайте число вслух: пять тысяч восемьсот двадцать семь.

Обратите внимание, что в этом числе есть четыре цифры. В результате развернутая форма будет содержать четыре слагаемых.

2. Перепишите число в виде суммы его цифр, оставив между ними некоторое расстояние, чтобы умножить каждую цифру на некоторую цифру (об этом далее).

Пример:
5827 перепишите так:

3. Цифры числа расположены в определенных позициях, которые соответствуют (справа налево) единицам, десяткам, сотням, тысячам и так далее. Определите название позиции и ее значение для каждой цифры (справа налево).

Пример:
Так как в данном числе четыре цифры, то вам нужно определить названия четырех позиций (справа налево).

7 соответствует единицам (значение = 1 = 10 0 ).
2 соответствует десяткам (значение = 10 = 10 1 ).
8 соответствует сотням (значение = 100 = 10 2 ).
5 соответствует тысячам (значение = 1000 = 10 3 ).

4. Умножьте каждую цифру данного числа на значение соответствующей ей позиции.

Пример:
5 · 10 3 + 8 · 10 2 + 2 · 10 1 + 7 · 10 0

Источник

Записать десятичные числа в развернутой форме

Любой вид информации можно представить в виде чисел. Кодирование информации с помощью чисел осуществляется по определённым правилам. Для понимания этих правил, разберём логику образования любого числа.

| Система счисления – это правила записи чисел с помощью знаков – цифр и операций над ними.

Любое число, в данной системе счисления, образуется путём повторения одинаковых элементов (палочка, камешек, ракушка и т.д.).

Данная система счисления позволяет записывать только натуральные числа и запись «большого» числа получается очень громоздкой.

В дальнейшем, у человечества возникла необходимость производить серьёзные подсчёты. Для этого были придуманы непозиционные системы счисления.

| Непозиционная система счисления – это система счисления, в которой цифра не изменяет своего значения, от изменения позиции в числе.

Египетская система счисления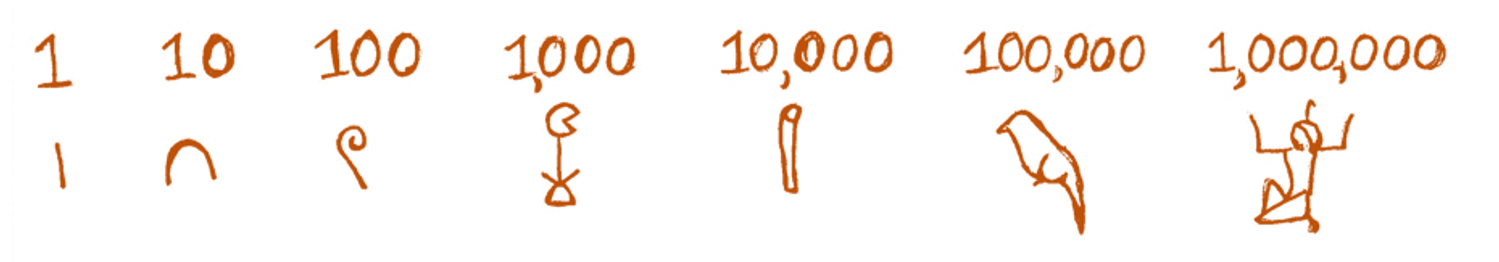
Кириллическая система счисления
Римская система счисления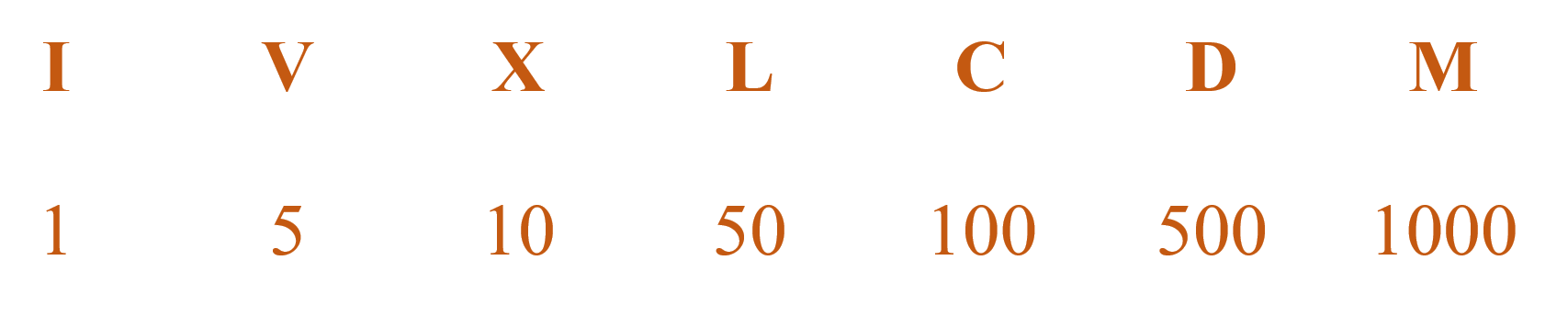
| Позиционная система счисления – это система счисления, в которой цифра изменяет своё значения, при изменении позиции в числе.

Вспомним, что любое число в десятичной (арабской) системе счисления можно разложить на разряды. Например, в числе 753 цифра 7 обозначает сотни (700), цифра 5 – десятки (50), цифра 3 – единицы. Таким образом, число можно представить, как:

753 = 7 * 100 + 5 * 10 + 3 * 1
| Алфавит системы счисления – совокупность всех её цифр.

| Основание системы счисления – указывает на количество цифр в данной системе счисления.

Алфавит десятичной системы счисления состоит из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Следовательно, основанием данной системы счисления является 10.

Тогда, любое число будем записывать по правилу, с указанием основания данной системы счисления:

Число читается, как «семьсот пятьдесят три по основанию десять» или «семьсот пятьдесят три в десятичной системе счисления».

| Разряд – это позиция цифры в числе (нумерация в целых числах производится с права налево, начиная с нуля).

Укажем разряд каждой цифры в числе 753:

Развёрнутая форма представления чисел

В результате разбиения числа на разряды, любое такое число можно представить в развёрнутой форме.

Формула развёрнутой формы представления чисел:

q – основание системы счисления;

a – цифра данного числа;

n – число разрядов в числе.

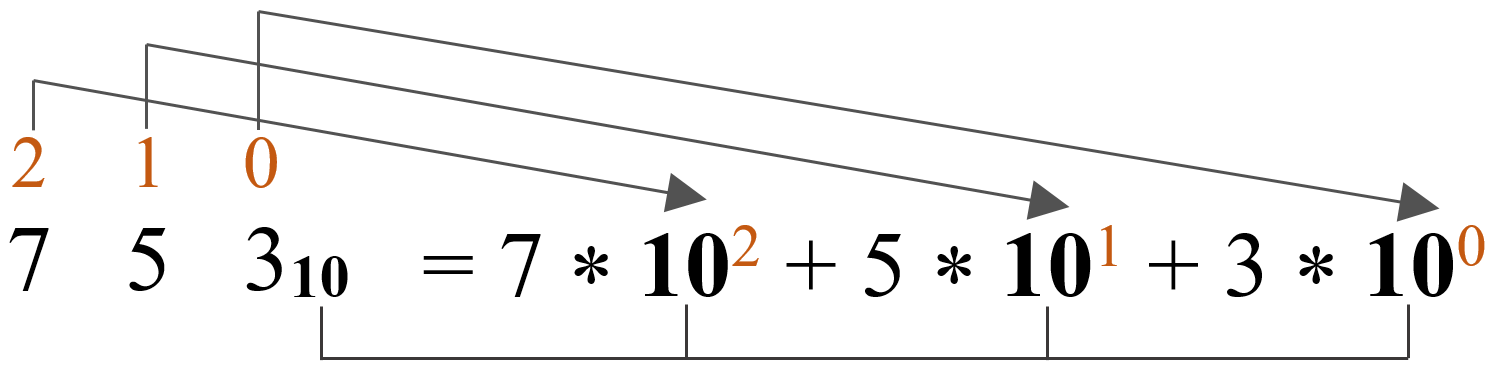
Представим число 75310 в развёрнутой форме.

1) Определим позиции каждой цифры в числе:

Каждую цифру в числе, умножим в соответствии занимаемой позицией:

Для упрощения данной записи, представим данное число, как основание 10 в степени n:

Запишем полученный результат.

Обратите внимание, что степень основания числа совпадает с позицией каждой цифры в числе!

Перевод числа в десятичную систему счисления

С помощью развёрнутой формы представления чисел можно перевести число из любой системы счисления в десятичную.

✒ Определение: каждую цифру числа нужно умножить на его основание, возведённое в степень, равную позиции цифры в числе.

Двоичная система счисления

Алфавит системы счисления: 0, 1.

Перевод десятичного числа в двоичную систему счисления методом подбора степеней числа 2

Для перевода двоичных чисел в десятичную систему счисления, используют метод подбора степеней двойки.

Пусть дано десятичное число 21_10.

1) Подберём ближайшую наименьшую степень числа 2 к данному числу: 2 4 = 16;

3) Повторить, пока не достигнем нуля.

В результате, мы получим следующие степени:

Найденные нами степени – это позиции цифры 1 в двоичном числе, а отсутствующие степени – это нули:

Перевод целого десятичного числа в другую систему счисления методом деления на новое основание

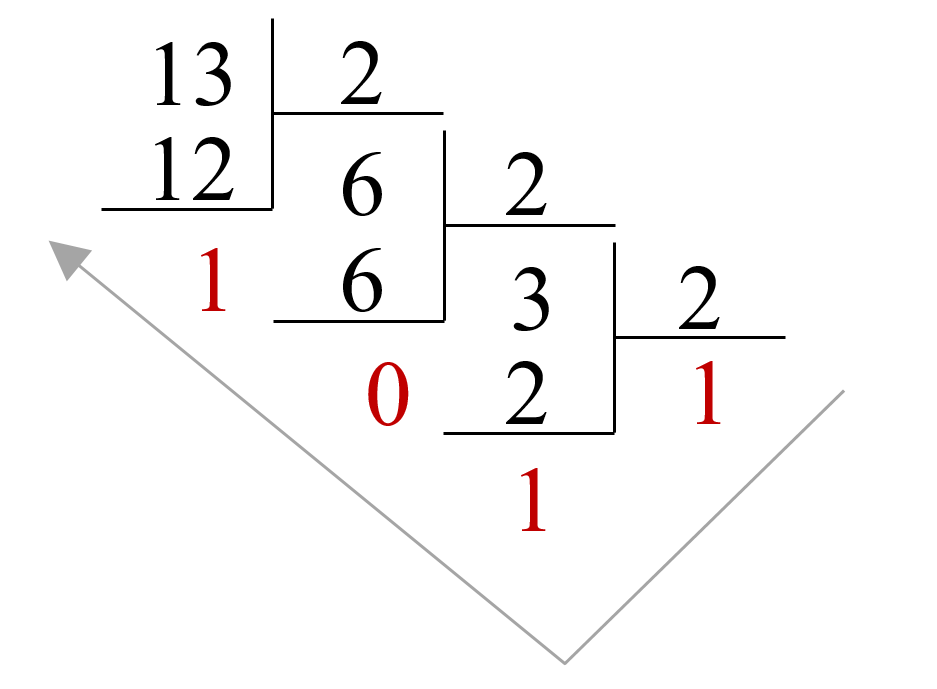
✒ Определение: Для перевода целого десятичного числа в другую систему счисления, необходимо делить данное число на новое основание (той системы счисления, в которую необходимо осуществить перевод). Ответ складывается из остатков от деления.

Переведите число 13₁₀ в двоичную систему счисления.

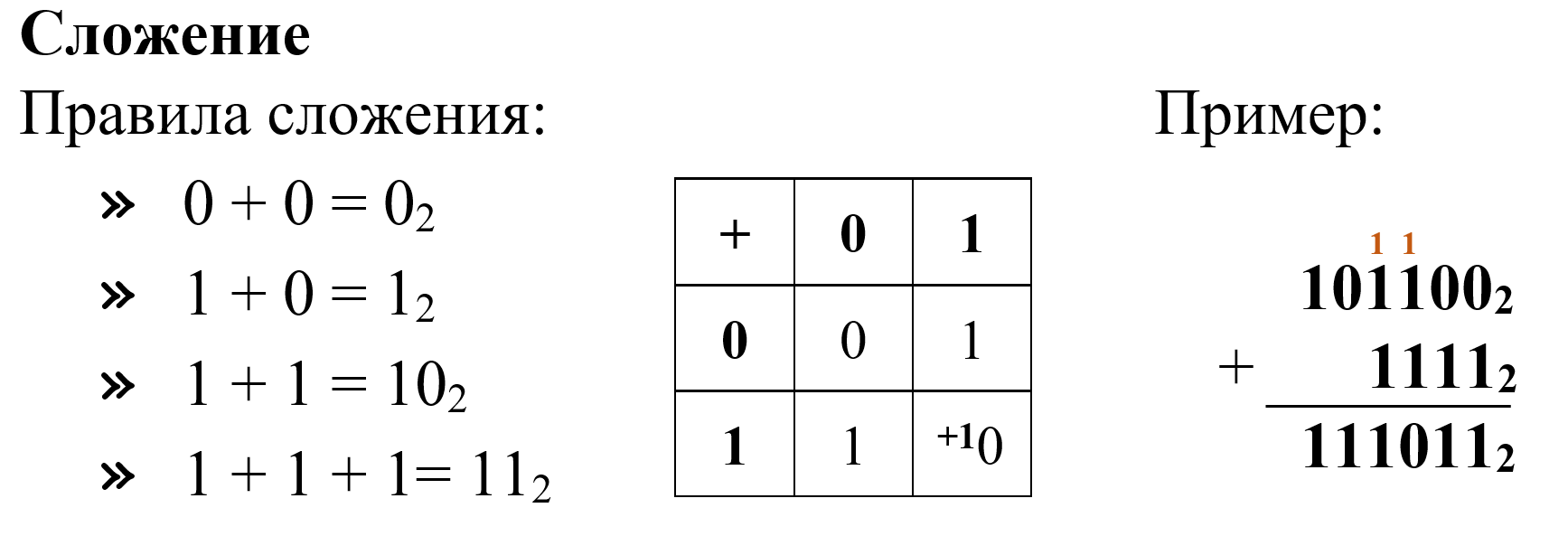
Арифметические операции в двоичной системе счисления

Все вычисления в компьютере выполняются в двоичной системе счисления.

Рассмотрим базовые арифметические операции.

Кодирование числовой информации в памяти компьютера

Для представления целого числа без знака в памяти компьютера, необходимо:

1. перевести число в двоичную систему счисления;

2. поместить число в ячейку памяти компьютера;

3. заполнить пустые ячейки незначащими нулями.

Представьте число 56₁₀ в компьютерной форме.

1. переведём число в двоичную систему счисления:

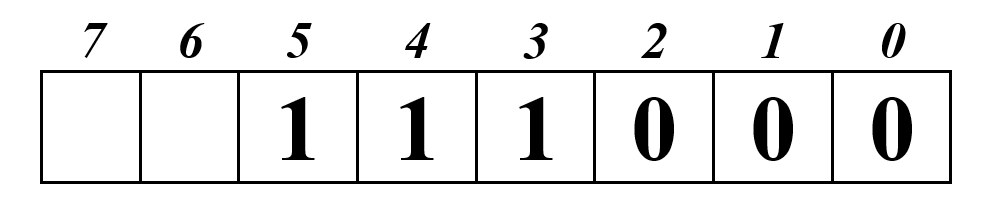
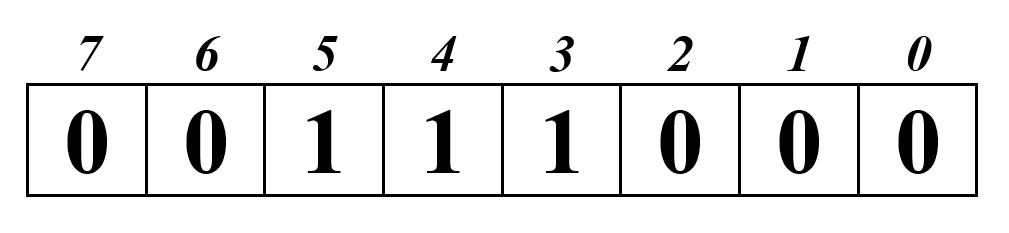
2. число состоит из 6 разрядов и помещается в одну ячейку:

3. дополним незначащими нулями:

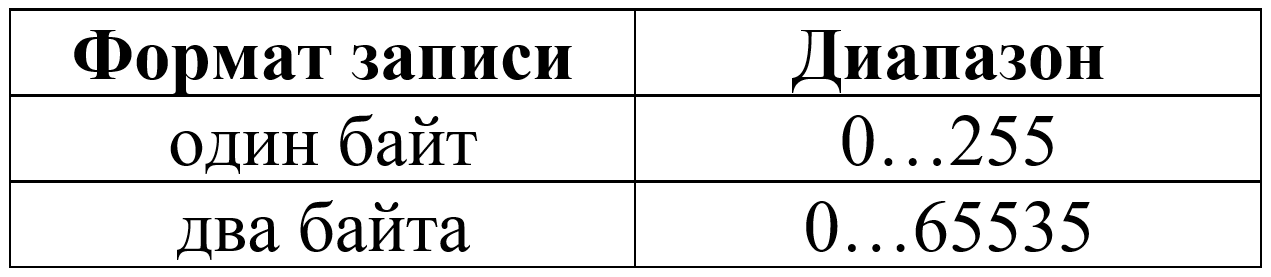
Диапазон значений целых чисел без знака

Хранение чисел со знаком отличается от беззнаковой формы.

Знак «+» принято обозначать за «0», а знак «–» за «1». Знак записывается в старший бит ячейки. Для хранения таких чисел выделяют 1, 2 или 4 байта.

Для представления целого числа со знаком «+» в памяти компьютера, необходимо:

1. перевести число в двоичную систему счисления;

2. поместить число в ячейку памяти;

3. выделить старший бит ячейки под знак и поставить на это место нуль.

4. заполнить оставшиеся биты незначащими нулями.

Представьте число +292₁₀ в компьютерной форме.

1. переведём число в двоичную систему счисления:

2. число состоит из 9 разрядов и для хранения требует двух ячеек:

3. число положительное, значит в старший бит необходимо поместить нуль:

4. заполним оставшиеся биты незначащими нулями:

Для представления целого числа со знаком «–» в памяти компьютера применяют метод прямого и обратного кода:

1. перевести модуль данного числа в двоичную систему;

2. Прямой код: поместить число в ячейку памяти и дополнить его незначащими нулями;

3. Обратный код: выполнить инверсию (заменить нули на единицы и наоборот);

4. Дополнительный код: увеличить получившееся число на единицу.

Представьте число –87₁₀ в компьютерной форме.

1. переведём модуль числа в двоичную систему счисления:

2. число состоит из 7 разрядов и помещается в одну ячейку. Поместим число в ячейку и дополним незначащими нулями:

4. прибавляем к числу единицу:

Обратите внимание на старший бит. Здесь 1 – это знак числа.

Переводы

1. Выполните перевод чисел из двоичной системы счисления в десятичную систему методом развёрнутой формы представления числа:

а) 1100₂	д) 1100011₂	з) 1001110111000₂
б) 11000₂	е) 100101101₂	к) 1001000010111₂
в) 101010₂	ж) 101110110₂	л) 101110101111₂
г) 1100011₂	з) 111111₂	м) 1111111₂

2. Выполните перевод из десятичной системы счисления в двоичную методом подбора степеней числа 2:

а) 42	д) 232	з) 400
б) 97	е) 286	к) 405
в) 111	ж) 309	л) 528

3. Выполните перевод из десятичной системы счисления в двоичную методом деления на новое основание:

а) 20	д) 100	з) 568
б) 31	е) 102	к) 443
в) 49	ж) 127	л) 500
г) 96	з) 269	м) 600

Арифметические операции в двоичной СС

4. Выполните сложение чисел:

а) 1001₂ + 1100₂	д) 100001₂ + 11000₂
б) 1010₂ + 1010₂	е) 101110₂ + 1010100₂
в) 111001₂ + 110110₂	ж) 1011111₂ + 1011111₂
г) 101010₂ + 110011₂	з) 1111011₂ + 1111001₂

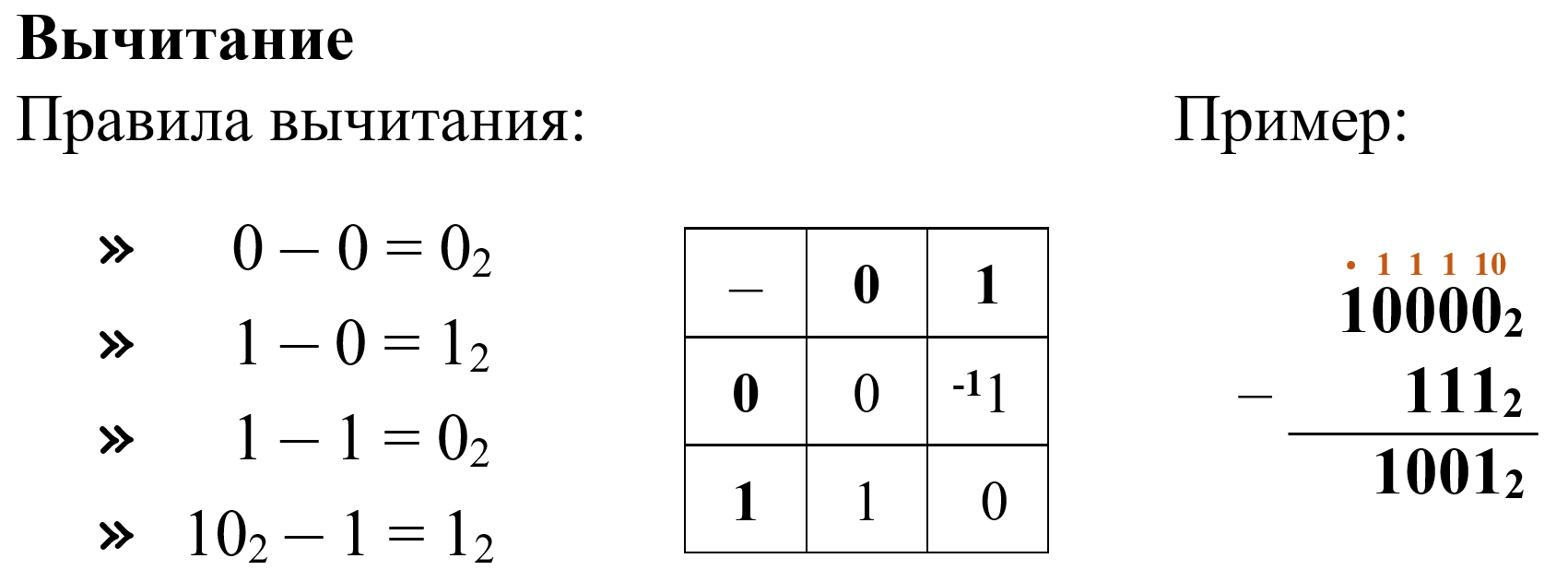
5. Выполните вычитание чисел:

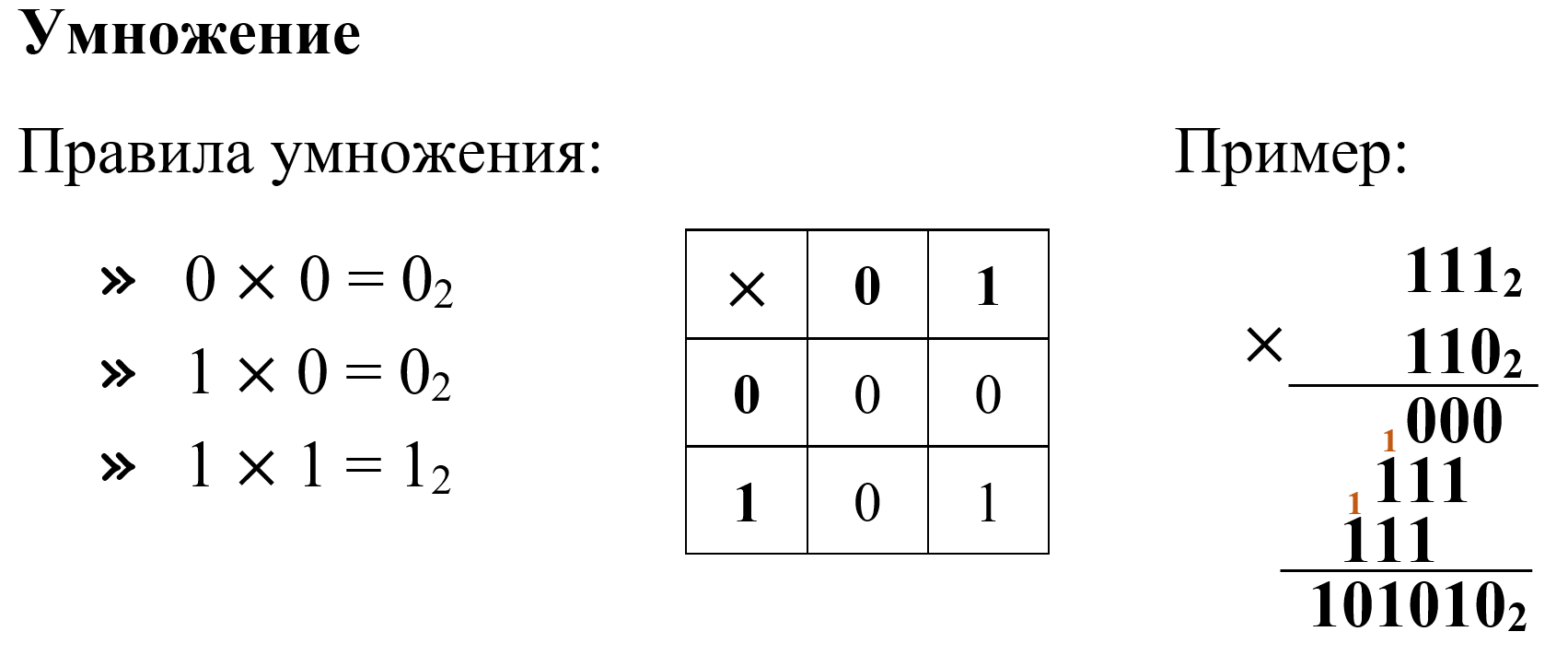
6. Выполните умножение чисел:

а) 1100₂ × 101₂	д) 101100₂ × 1011₂
б) 1010₂ × 111₂	е) 101111₂ × 1101₂
в) 11011₂ × 1011₂	ж) 101101₂ × 1111₂
г) 11110₂ × 1011₂	з) 101011₂ × 1110₂

7. Найти значение выражения:

Кодирование чисел

8. Представьте целое десятичное число со знаком в памяти компьютера. Сколько ячеек памяти нужно выделить для хранения данного числа?

а) +25	д) +204	з) +512
б) +64	е) +212	к) +4096
в) +96	ж) +256	л) +32256
г) +128	з) +302	м) +65536

9. Представьте целое десятичное число со знаком в памяти компьютера. Сколько ячеек памяти нужно выделить для хранения данного числа?

10. Дано внутреннее представление целого числа со знаком. Какому десятичному числу оно соответствует?

Источник

Как записать число в развернутой форме информатика

2.5. РАЗВЕРНУТАЯ ФОРМА ЧИСЛА

Развернутая форма записи числа – это запись в виде разрядных слагаемых, записанных с помощью степени соответствующего разряда и основания степени (основание счета).

1. Десятичная система:

Пронумеруем разряды, начиная с младшего:

Теперь запишем выражение:

2. Двоичная система:

Пронумеруем разряды, начиная с младшего:

3. Шестнадцатеричная система:

Пронумеруем разряды, начиная с младшего:

Другие системы счисления записываются аналогично вышеприведенным системам с тем лишь исключением, что основание степени будет соответствовать основанию счета.

В позиционной системе счисления число можно представить в развернутой форме (в виде суммы разрядных слагаемых) и в свернутой форме. Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.

Десятичное число А₁₀= 4718,63 в развернутой форме будет имеет вид:

Рассмотрим еще примеры записи чисел в развернутом виде

589₁₀ → 500 + 80 + 9 = 5*100 + 8*10 + 9*1 = 5*10 2 +8*10 1 + 9*10 0

₁₀ = 5*10 2 + 8*10 1 + 9*10 0

= 4*10 5 + 8*10 4 + 5*10 3 + 7*10 2 + 6*10 1 + 3*10 0

= 1*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 0*2 0

= 7*8 2 + 6*8 1 + 4*8 0

= 7*16 2 + 6*16 1 + 4*16 0

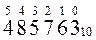
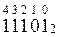
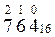
Задания для самостоятельной работы

Задание 1. Запишите числа в развернутой форме

1)	1111010₂	6)	111101,001₂	11)	1110,11₂	16)	10001110₂
2)	2174,5₅	7)	5771,001₅	12)	8978451₅	17)	51476317₅
3)	647911₈	8)	1622,84₈	13)	111487₈	18)	113874,334₈
4)	12147₁₀	9)	5120014₁₀	14)	1874,596₁₀	19)	1554,014₁₀
5)	1247,0321₁₆	10)	157894₁₆	15)	163201,98₁₆	20)	885412₁₆

Перевод чисел в десятичную систему счисления

1. Записать число в развернутом виде

2. Выполнить вычисления как в десятичной системе счисления

→ 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 + 0*2 0 = 1*16 + 0*8 + 1*4 + 0*2 + 1*1 = 16 + 0 + 4 + 0 + 1 = 21₁₀

→ 3*8 2 + 4*8 1 + 7*8 0 = 3*64 + 4*8 + 7*1 = 192 + 32 + 7 = 231₁₀

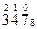
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10571 – | 7330 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно