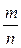збч в форме чебышева

Как работает Закон больших чисел – Примеры в реальной жизни

Как начать торговать на бирже: Инструкции и Примеры, Обучение

Примеры работы закона больших чисел в разных областях и отраслях. Чем отличаются ЗБЧ от Чебышева и Бернулли и как их применять в своей жизни.

Этот термин пришел из теории вероятности, закон больших чисел показывает насколько близким окажется среднее значение выборки к математическому ожиданию для одного и того же распределения.

Звучит несколько непонятно, ниже подробнее остановимся на физическом смысле этого закона и методах его применения в разных сферах человеческой деятельности.

Этот закон применяется и в инвестировании, и в здравоохранении, и в сфере страхования – везде, где нужно анализировать массив информации.

Что такое закон больших чисел

Для начала разберемся с терминами:

Закон больших чисел простыми словами – это закон, позволяющий понять, каким вероятнее всего окажется результат эксперимента, если проводить его неоднократно. Чем большим будет число таких экспериментов, тем ближе будет результат к математическому ожиданию.

Более того, закон больших чисел – это та закономерность, которая позволяет прогнозировать исход случайных событий на длинной дистанции. Это важно в прогнозировании и оценке рисков в любой сфере деятельности человека.

Если заинтересуетесь доказательствами этого, рекомендуем углубиться в теорию вероятности. Так, доказательство закона больших чисел Чебышева показывает, что среднее арифметическое при приближении числа экспериментов к бесконечности практически уравнивается с матожиданием.

Схожее доказательство есть для закона больших чисел Бернулли. В нем доказывается, что при неограниченно большом количестве экспериментов частота проявления определенного события оказывается равной вероятности его появления.

Помимо обычного есть и усиленный закон больших чисел. В обычном матожидание может бесконечное количество раз сильно отличаться от среднего значения результата экспериментов (происходит это бесконечно редко). В усиленном же законе вероятность такого отличие сведена к нулю, то есть со 100%-ной вероятностью матожидание сводится к арифметическому среднему.

Сущность закона больших чисел

Для визуализации закона представьте себе подбрасывание монетки. Вероятность выпадения одной из сторон 50%, если подбросить ее 10 раз, то распределение может оказаться и 70/30 и 20/80.

Но если продолжать эксперимент 10000, 1000000 раз, то распределение будет приближаться к 50/50. То есть частота проявления каждого события на дистанции стремится к вероятности его появления.

Еще один пример – подбрасывание кубиков (вернее одного кубика). В каждом эксперименте может выпасть число от 1 до 6, но закон больших чисел утверждает, что на длинной дистанции среднее арифметическое суммы бросков приближается к 3,5. Результаты эксперимента доказывают это на практике.

Похожую закономерность можно найти, например, при исследовании результатов общения страховых агентов с потенциальными клиентами. При большой выборке окажется, что в среднем на 1000 звонков приходится определенное количество заключенных договоров. Так что важно понимать суть закона больших чисел, он работает в любой сфере.

Без использования этого закона было бы невозможно планировать развитие бизнеса и оценивать эффективность работы в прошлом.

Как использовать закон больших чисел инвестору

Зная, что понимается под законом больших чисел инвестор может прогнозировать результаты вложений.

Работа со статистикой в этом и заключается, инвестиционная стратегия проверяется на истории, рассчитывается математическое ожидание, коэффициент Шарпа, Сортино и прочие характеристики.

Если для исследования взять достаточно продолжительный временной отрезок, то в будущем при использовании этой инвестиционной стратегии результат вероятнее всего окажется близок к полученному на истории.

Простейший пример оценки стстратегии:

Ответьте на вопрос – стоит ли работать при таких условиях?

Например, алгоритмические хедж-фонды работают с сотнями/тысячами стратегий, нацеленных на сотни различных инструментов. Обязательное требование для включения стратегии в пул – положительное математическое ожидание. При работе с инструментами с с максимальной отрицательной корреляции, это делает работу практически безубыточной.

Рядовой инвестор также использует понятие о законе больших чисел (даже если не владеет терминологией из теории вероятности). Вспомните как проводится анализ любого инвестиционного портфеля:

Эта схема – типичное использование закона больших чисел, ей следуют все опытные инвесторы.

Разберем этот метод на примере инвестиций в ETF с тикером SPY.

Для тестирования выберем любой временной промежуток, например, 2010-2016 гг.. В отчете нас интересует математическое ожидание или средний арифметический прирост капитала в год и в месяц.

Есть еще и средний геометрический прирост, он рассчитывается на основании наклона кривой роста депозита, при стабильном росте капитала средний арифметический и геометрический прирост практически совпадают.

Теперь проведем форвард-тест (взяв участок истории после 2016 г.). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат.

Ожидания оправдались – рассчитывали на среднюю месячную и годовую доходность на уровне 1,07% и 13,62%, а при форвард-тесте получили 1,20% и 15,42%. Расхождение составило 12,2% и 13,2%, что для не особенно длинной дистанции неплохой результат.

Закон больших чисел просто показывает каким вероятнее всего будет результат случайного события. Но он не гарантирует, что в каждом следующем испытании итог будет строго равен математическому ожиданию.

За период с февраля 1993 г. по конец 2000 г. SPY показал себя отлично. Опираясь на статистику, инвестор мог рассчитывать на средний профит в 17,98% в год или 1,39% в месяц.

Но после 2000 г. начался спад и фонд просел, инвестор получил убыток. На короткой дистанции могло показаться, что закон перестал работать и пора искать новый инструмент для вложений.

В следующие пару лет ETF SPY был убыточным. Вместо роста капитала инвестор получил убыток в среднем 15,19% в год или 1,36% в месяц. Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя.

Причина таких расхождений – работа с небольшими временными промежутками. Здесь уместна аналогия с подбрасыванием монетки:

То же и в инвестировании. Вспомните сущность закона больших чисел, он применим только при достаточном массиве статистики.

Если вернуться к ETF SPY и оценить его показатели за все время существования, то окажется, что рассчитывать можно в среднем на рост в 10,83% за год и 0,86% в месяц.

Этим результатам стоит доверять больше еще и потому, что за выбранный период SPY успел пережить 2 кризиса.

Ровно по такой же схеме закон больших чисел используется и в хедж-фондах, управляющих миллиардами долларов. Отличаются лишь инструменты анализа информации, сам принцип остается тем же.

Как использовать закон больших чисел в бизнесе

Закон больших чисел связан с обработкой статистических данных. Крупный бизнес не сможет работать и прогнозировать развитие без обработки статистики, поэтому этот закон в бизнесе применяется повсеместно.

Ниже – варианты применения закона в различных секторах:

Закон больших чисел в бизнесе применяется повсеместно. Прогнозирование результатов в будущем – не единственное его применение.

Так, закон больших чисел описывает фазы развития бизнеса. В частности, из него следует, что темпы роста бизнеса в процентном соотношении не могут сохраняться постоянными неограниченно долго.

Отсюда следует, что у молодого бизнеса более вероятен резкий рост, чем у компаний с многомиллиардными оборотами. Это следует взять на вооружение инвесторам.

По мере роста происходит насыщение рынка, рост в процентном соотношении падает (при этом в деньгах показатели растут). Чтобы не перейти к стагнации компания выводит новые продукты, выходит на новые рынки.

Применение закона больших чисел в банковской деятельности

Закон больших чисел просто необходим в банковской сфере.

В кредитовании. Например, чтобы обосновать проценты по кредиту. Использовав закон больших чисел банк может спрогнозировать какая доля заемщиков не выплатит займ. В том числе исходя из этого назначается процент за использование кредитных денег.

Для составления профиля благонадежного и неблагонадежного заемщика. На основании этого закона составляется профиль заемщика, который с наибольшей вероятностью вернет займ. Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.

Что касается того, на чем основывается закон больших чисел при его применении в банковской сфере, то это тот же массив статистики.

Эта закономерность используется и другими околофинансовыми учреждениями. Например, БКИ при расчете кредитного рейтинга и прогнозе о возможности займа в банке опираются на анализ статистики. Значит закон больших чисел задействован и здесь.

Как работает закон больших чисел в страховании

Сектор страхования предлагает всем желающим (не только физлицам) защитить себя от убытков при наступлении несчастного случая.

На первый взгляд форс-мажоры спрогнозировать невозможно, но при изучении статистики оказывается, что и они подчиняются математическим закономерностям.

Закон больших чисел в страховании используется для определения минимального страхового взноса, который бы позволил компании перекрыть убытки при наступлении страхового случая.

Пример

Закон больших чисел говорит о том, что в среднем за год вероятность попадания в ДТП/угона (условия наступления страхового случая оговариваются отдельно) составляет 1/200 или 0,5%. То есть ежегодно страховщику придется выплачивать компенсацию 0,5 х 100000/100 = 500 автовладельцам.

Страхование – бизнес, который стал возможным исключительно благодаря закону больших чисел. Без прогнозирования соотношения прибыли и убытка по страховым случаям страховщики не стали бы работать.

Когда закон больших чисел не работает

Сложно найти сферу деятельности человека, где не применяется закон больших чисел. Но сама по себе эта закономерность не является 100%-ной гарантией того, что в будущем события будут развиваться в соответствии с расчетами.

Закон больших чисел может не работать при:

Это не значит, что закон больших чисел нельзя использовать в бизнесе и инвестировании. Просто нужно заранее понимать, что он лишь прогнозирует вероятный результат в будущем на основе статистики.

Заключение

Если дать определение закону больших чисел простым языком, его можно назвать законом, описывающим наиболее вероятный сценарий развития событий в будущем, опираясь на массив исторических данных. При этом он не гарантирует на 100%, что результаты окажутся точно такими же.

Эту закономерность использует любой бизнес без исключения, в инвестировании ей также отведена существенная роль.

Вероятнее всего вы и сами неосознанно пользуетесь этой закономерностью при планировании своих инвестиций. Если же нет – самое время начать это делать.

Трейдер, инвестор, частный предприниматель. «Финансовые рынки объединяют разные интересы, бизнес, континенты. Это то место, где всегда можно найти, чем заняться, что и как сделать или создать.»

Источник

Закон больших чисел и то, чем он не является

О законе больших чисел (збч) написано много (например, на английском, тут и тут, также [1]). В этом тексте я попробую рассказать о том, чем закон больших чисел не является – об ошибочном восприятии этого закона и потенциальных ловушках, спрятанных в математических формулировках.

Начнем с того, что же такое закон больших чисел. Неформально, это математическая теорема о том, что «вероятность отклонений среднего по выборке от математческого ожидания мала» и что «эта вероятность стремится к нулю при увеличении выборки». Совсем неформально, теорема утверждает, что с мы можем быть в достаточной степени уверены, что среднее по нашей выборке достаточно близко к «настоящему» среднему и таким образом хорошо его описывает. Разумеется, предполагается наличие традиционного статистического «багажа» — наши наблюдения из выборки должны описывать одно и то же явление, они должны быть независимы, и мысль о том, что есть некоторое «настоящее» распределение с «настоящим» средним, не должна вызывать у нас существенных сомнений.

При формулировке закона мы говорим «среднее по выборке», и все что может быть математически записано как такое среднее, попадает под действие закона. Например, доля событий в общей массе может быть записана как среднее, — нам достаточно записать наличие события как «1» и отсутствие как «0». В итоге среднее будет равно частоте и частота должна быть близка к теоретическому среднему. Именно поэтому по ожидаем, что доля «орлов» при подбрасывании идеальной монеты будет близка к ½.

Рассмотрим теперь ловушки и ошибочные представления об этом законе.

Во-первых, ЗБЧ не всегда верен. Это всего лишь математическая теорема с «входными данными» — предположениями. Если предположения неверны, то и закон не обязан выполняться. Например, это так если наблюдения зависимы, или если нет уверенности в том, что «настоящее» среднее существует и конечно, или если изучаемое явление меняется во времени и мы не можем утверждать, что мы наблюдаем одну и ту же величину. По правде говоря, в определенной степени ЗБЧ верен и в этих случаях, например, для слабокоррелированных наблюдений или даже в том случае когда наблюдаемая величина меняется во времени. Однако, для корректного приложения этого к непосредственной реальности нужен хорошо тренированный специалист-математик.

Во-вторых, кажется верным, что ЗБЧ утверждает «среднее по выборке близко к настоящему среднему». Однако, такое утверждаение остается не полным: надо обязательно добавлять «с высокой долей вероятности; и эта вероятность всегда меньше 100%».

В-третьих, хочется сформулировать ЗБЧ как «среднее по выборке сходится к настоящему среднему при неограниченном росте выборки». Однако, это неверно, потому что среднее по выборке вообще никуда не сходится, так как оно случайное и остается таковым для любого размера выборки. Например, даже если подбросить симметричную монету миллион раз, все равное есть шанс, что доля орлов будет далека от ½ или даже равна нулю. В определенном смысле, всегда есть шанс получить что-то необычное. Надо признать, однако, что наша интуиция все-таки подсказыает нам что ЗБЧ должен описывать какую-то сходимость, и так есть на самом деле. Только «сходится» не среднее, а «вероятность отклонения выборочного среднего от его истинного значения», и сходится к нулю. Так как эта идея интуитивно очень удобна («шансы увидеть что-то необычное стремятся к нулю»), матетматики придумали для этого особый тип сходимости – «сходимость по вероятности».

В-четвертых, ЗБЧ не говорит ничего о том, когда выборочное среднее можно считать достаточно близким к теоретическому. Закон больших чисел только постулирует существование определенного явления, он ничего не говорит о том, когда его можно использовать. Получается, на ключевой вопрос с точки зрения практики — «могу ли я использовать ЗБЧ для моей выборки размера n?», закон больших чисел не отвечает. Ответы на эти вопросы дают другие теоремы, например, Центральная Предельная Теорема. Она дает представление о том, в каких пределах выборочное среднее может отклоняться от своего истинного значения.

В заключение следует отметить центральную роль ЗБЧ в статистике и теории вероятностей. История этого закона началась тогда, когда ученые заметили, что частоты некоторых повторяющихся явлений стабилизируются и перестают существенно меняться, при условии многократного повторения опыта или наблюдения. Поразительным было то, что эта «стабилизация частот» наблюдалась для совершенно несвязаных явления – от бросания игральной кости до урожайности в сельском хозяйстве, указывая на возможное существование «закона природы». Интересно, что этот закон природы оказался частью математики, а не физики, химии или биологии, как обычно бывает с законами природы.

[1] Illustrating the Law of Large Numbers (and Confidence Intervals) Jeffrey D Blume & Richard M Royall

Источник

Неравенство Маркова. Неравенство Чебышева

На этой странице мы собрали примеры решения учебных задач по теории вероятностей, в которых применяются неравенство Маркова, неравенство Чебышева, теорема Чебышева и их следствия (закон больших чисел, ЗБЧ).

Краткая теория. Закон больших чисел

Неравенство Маркова дает вероятностную оценку того, что значение неотрицательной случайной величины превзойдет некоторую константу через известное математическое ожидание. Когда никаких других данных о распределении нет, неравенство дает некоторую информацию, хотя зачастую оценка груба или тривиальна.

Альтернативная форма записи (когда нужно оценить вероятность того, что СВ меньше некоторой константы):

Когда известны не только математическое ожидание (первый момент), но и дисперсия (второй центральный момент) для случайной величины (и они конечны), можно применять следствие неравенства Маркова — неравенство Чебышева, которое дает оценку вида:

Также его можно записать в другой форме:

Приведем также теорему Чебышева, которая имеет большое практические значение.

Примеры решенных задач

Неравенство Маркова: примеры решений

Задача 1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500.

Задача 2. Количество потребляемой за сутки электроэнергии предприятием является случайной величиной с математическим ожиданием 6 мегаватт при среднем квадратическом отклонении 1,5 мегаватта. Оценить вероятность того, что в ближайшие сутки потребление электроэнергии окажется более 12 мегаватт.

Неравенство Чебышева: примеры решений

Задача 4. В 1600 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,3. С помощью неравенства Чебышева оценить вероятность того, что разница между числом успехов в этих испытаниях и средним числом успехов будет меньше 50.

Задача 6. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух.

Теорема Чебышева и ЗБЧ: примеры решений

Задача 8. Вероятность того, что абсолютная величина отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не превышает 0,5, равна 0,8. Дисперсия каждой независимой случайной величины не превышает 7. Найти число таких случайных величин.

Задача 9. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.

Решебник по терверу

Нужны еще решения? Найди в решебнике сейчас:

Источник

Закон больших чисел в форме Чебышева

Если явление устойчивости средних имеет место в действительности, то в математической модели, с помощью которой мы изучаем случайные явления, должна существовать отражающая этот факт теорема.
В условиях этой теоремы введем ограничения на случайные величины X₁, X₂, …, X_n:

а) каждая случайная величина Х_i имеет математическое ожидание

б) дисперсия каждой случайной величины конечна или, можно сказать, что дисперсии ограничены сверху одним и тем же числом, например С, т. е.

Доказательство. Для конечного числа n независимых испытаний применим неравенство Чебышева для случайной величины = :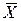

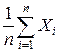
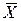
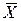
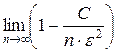
Р(|– M()| 0и n ® ¥, то получим

= 1,

что и доказывает теорему Чебышева.

Из рассмотренной теоремы вытекает важный практический вывод: неизвестное нам значение математического ожидания случайной величины мы вправе заменить средним арифметическим значением, полученным по достаточно большому числу опытов. При этом, чем больше опытов для вычисления, тем с большей вероятностью (надежностью) можно ожидать, что связанная с этой заменой ошибка ( 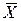– а)не превзойдет заданную величину ε.

Кроме того, можно решать другие практические задачи. Например, по значениям вероятности (надежности) Р = Р(|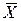– а|

Предположим, что испытания удовлетворяют следующим требованиям:

Учитывая вышеуказанные условия, получим

Р(|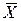– а|

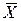
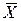
Пример4.1.2. Дисперсия случайной величины Х равна D(Х) = 5. Произведено 100 независимых опытов, по которым вычислено . Вместо неизвестного значения математического ожидания а принята . Определить максимальную величину ошибки, допускаемую при этом с вероятностью не менее 0,8.

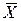
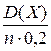
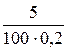
Решение.По условию задачи n = 100, Р(|– а| 2 = = = 0,25.

Следовательно, ε = 0,5.

Ответ: максимальная величина ошибки ε = 0,5.

4.2. Закон больших чисел в форме Бернулли [4]

Хотя в основе любого статистического вывода лежит понятие вероятности, мы лишь в немногих случаях можем определить вероятность события непосредственно. Иногда эту вероятность можно установить из соображений симметрии, равной возможности и т.п., но универсального метода, который позволял бы для произвольного события указать его вероятность, не существует. Теорема Бернулли дает возможность приближенной оценки вероятности, если для интересующего нас события А можно проводить повторные независимые испытания. Пусть произведено п независимых испытаний, в каждом из которых вероятность появления некоторого события А постоянна и равна р.

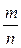
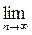
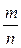
Теорема Бернулли. При неограниченном возрастании числа независимых испытаний п относительная частота появления события А сходится по вероятности к вероятности p появления события А,т. е.

P(½ — p ½≤ ε) = 1, (4.2.1)

где ε – сколь угодно малое положительное число.

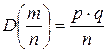
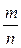
Для конечного n при условии, что , неравенство Чебышева для случайной величины будет иметь вид:

P(| 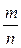– p| 2 = 1 2 ∙p + 0 2 ∙q – p 2 = p – p 2 = = p(1 – p) = pq.

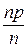
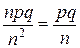
M(Y_n) = = p; D(Y_n) = ® 0.

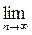
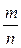
Следовательно, выполняются условия теоремы Чебышева, т. е. P(½ — p ½≤ ε) = 1, что и требовалось доказать.

Из теоремы Бернулли следует, что при достаточно большом числе испытаний относительная частота 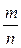появления события практически утрачивает свой случайный характер, приближаясь к постоянной величине p – вероятности данного события. В этом и состоит принцип практической уверенности.

Пример 4.2.1. С целью установления доли брака продукции было проверено по схеме возвратной выборки 1000 единиц. Какова вероятность того, что установленная этой выборкой доля брака по абсолютной величине будет отличаться от доли брака по всей партии не более чем на 0,01, если известно, что в среднем на каждые 10000 изделий приходится 500 бракованных?

Решение.По условию задачи число независимых испытаний n = 1000;

p = 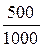= 0,05; q = 1 – p = 0,95; ε = 0,01.

Применяя формулу (4.2.2), получим

P(| – p|

Источник