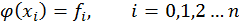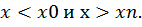Аппроксимация что это

29.08.202228.08.2022 admin 0 Комментариев

Аппроксимация что это

Значение слова «аппроксимация»

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.

В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

аппроксима́ция

1. матем. приближённое выражение некоторых величин или объектов через другие, более простые величины или объекты ◆ Вследствие того, что массы элементарных частиц распределены в пределах многих порядков, аппроксимацию распределения целесообразно представить в логарифмическом масштабе. Воспоминания о Шкловском, «1996» (цитата из НКРЯ) ◆ Коэффициент аппроксимации 6,8% свидетельствует о высокой степени согласия уравнения регрессии с фактическими величинами. «Прогноз необходимости борьбы с непарным шелкопрядом в нагорных дубравах», 2004 г. // «Лесное хозяйство» (цитата из НКРЯ)

2. перен. филос. метод приближения, указание на приблизительный, неокончательный характер чего-либо

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: начистую — это что-то нейтральное, положительное или отрицательное?

Источник

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ — АППРОКСИМАЦИЯ (от лат. approximare приближаться) метод сознательного упрощения “слишком точного” теоретического знания с целью привести его в соответствие с потребностями и возможностями практики. Напр., использование числа π с точностью до… … Философская энциклопедия

Аппроксимация — (approximation приближение) процедура выбора оптимальной аппроксимирующей функции из определенного класса функций. Следует различать параметрическую и непараметрическую аппроксимацию. При параметрической аппроксимации общий вид (формула, модель)… … Официальная терминология

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

аппроксимация — приближение; апроксимирование, апроксимация, линеаризация Словарь русских синонимов. аппроксимация сущ., кол во синонимов: 3 • апроксимация (2) • … Словарь синонимов

аппроксимация — и, ж. approximation, нем. Approximation <лат. approximare приближаться. мат. Приближенное выражение каких л. величин через другие, более простые величины. Крысин 1998. | Аппроксимация называется официальное снижение требований в школьной… … Исторический словарь галлицизмов русского языка

Аппроксимация — приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В экономике целью А. часто является укрупнение характеристик моделируемых экономических объектов. Словарь бизнес терминов. Академик.ру.… … Словарь бизнес-терминов

АППРОКСИМАЦИЯ — (от лат. approximo приближаюсь) замена одних математических объектов (напр., чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными) … Большой Энциклопедический словарь

АППРОКСИМАЦИЯ — приближенное выражение математических величин (чисел, функций и т. п.) через другие. Любую непрерывную функцию f(x), a ≤ х ≤ b можно аппроксимировать алгебраическими или тригонометрическими многочленами. Важно определить степень… … Геологическая энциклопедия

АППРОКСИМАЦИЯ — (от лат. approximare – приближаться). Обучение иноязычному произношению, ограниченное приближением к правильному произношению и допускающее «снисходительное отношение» к фонетическим ошибкам, не нарушающим коммуникацию. Однако А. не должна… … Новый словарь методических терминов и понятий (теория и практика обучения языкам)

Аппроксимация — [approximation] «замена одних математических объектов другими, в том или ином смысле близкими к исходным»[1] ; в частности приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Экономико-математический словарь

аппроксимация — «Замена одних математических объектов другими, в том или ином смысле близкими к исходным» [1]. В частности — приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Справочник технического переводчика

Источник

Что такое аппроксимация

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.

Сегодня рассмотрим один из них, термин «аппроксимация».

Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.

Аппроксимация в математике — это …

Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».

Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).

Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.

Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.

Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.

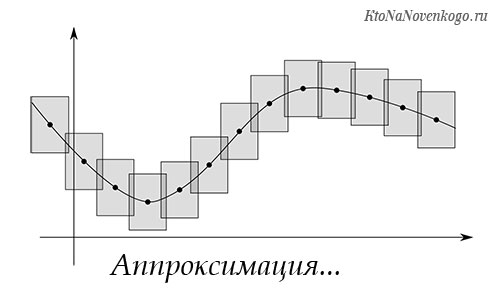
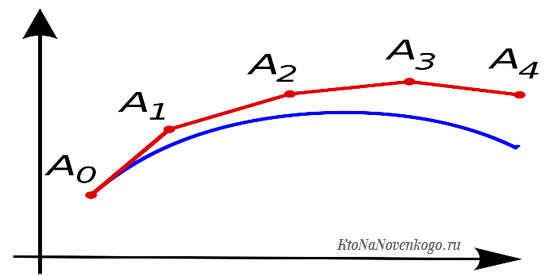
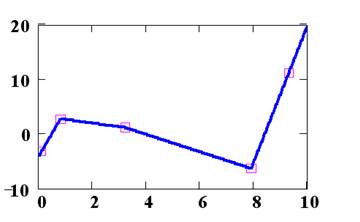
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:

Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.

Термин «аппроксимация» схож по сути со следующими математическими понятиями:

Применение термина «аппроксимация» в иных областях

Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.

Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).

Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.

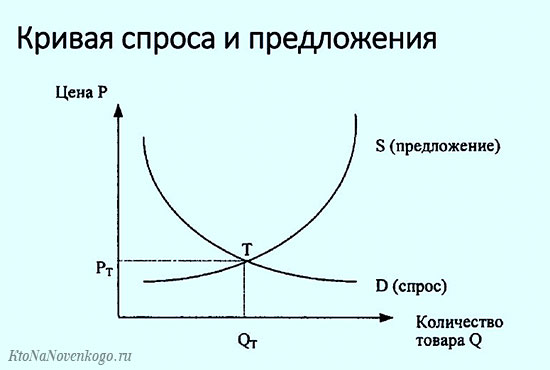
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:

На самом деле на спрос и предложение влияние оказывают и другие факторы.

При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.

Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».

Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.

Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.

Краткое резюме

Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.

Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.

Читайте наш блог, это познавательно!

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?

Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.

Источник

Аппроксимация

Добавлено в закладки: 0

Что такое аппроксимация – это научный метод, который можно использовать в разных областях познания. В дословном переводе он означает «приближение», и под ним подразумевается замена одних объектов, которые изучаются, на другие, схожие с исходными и более простые.

Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.

Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.

Рассмотрим, более детально, ч то значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.

Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.

В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

Остаточный член

Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.

Примеры

Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.

Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.

Мы надеемся, что да ли наиболее полное определение и понятие термина аппроксимация, привели ее примеры

Источник

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

Источник

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

Аппроксимация

Аппроксимация — это метод сознательного упрощения излишне сложного теоретического знания с целью привести его в соответствие с потребностями и возможностями практики. Метод аппроксимации первоначально использовался в математике и затем распространился на другие науки. В математике аппроксимация подразумевает замену одних математических объектов (например, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным. Так, использование числа n с точностью до пятого знака после запятой достаточно для решения поставленной практической задачи. В прикладных науках метод аппроксимации в общем случае подразумевает приближённое выражение сложной функции с помощью более простых функций. В практике управления (см. Управление) целью аппроксимации часто является укрупнение характеристик моделируемых [системных] объектов (например, приближённое выражение характеристик сложной системы или объекта через другие, более простые системы, объекты), что значительно упрощает решение оптимизационных задач, особенно при управлении крупными и сложными системами (см. Системный анализ и Системная инженерия).

Источник

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

АППРОКСИМАЦИЯ

Найдено 1 изображение:

— аппроксимация импульсной функции
— аппроксимация Паде
— аппроксимация по методу наименьших квадратов
— аппроксимация полиномами
— аппроксимация ступенчатой функции непрерывной функцией
— аппроксимация функцией
— аппроксимация функции
— бикубическая аппроксимация
— графическая аппроксимация
— грубая аппроксимация
— двумерная аппроксимация
— двухступенчатая аппроксимация
— жёсткая аппроксимация
— изопараметрическая аппроксимация
— импульсная аппроксимация
— квадратичная аппроксимация
— конечноэлементная аппроксимация
— кусочная аппроксимация
— кусочно-линейная аппроксимация
— линейная аппроксимация
— линейная симплексная аппроксимация
— ограниченная аппроксимация
— полиномиальная аппроксимация
— полудискретная аппроксимация
— поточечная аппроксимация
— прямолинейная аппроксимация
— разностная аппроксимация вперёд
— разностная аппроксимация назад
— симплексная аппроксимация
— сопряжённые аппроксимации
— статистическая аппроксимация
— субпараметрическая аппроксимация
— триквадратичная аппроксимация
— трикубическая аппроксимация
— трилинейная аппроксимация
— центральная разностная аппроксимация

При выполнении определенных условий f(x) можно аппроксимировать конечной суммой ряда Тейлора или Фурье или конечными суммами других рядов. Типичным примером использования А. в геологии является решение задач по расчету тренда. См. Тренд-анализ.

Источник:

«АНАЛИЗ ПОВОЗРАСТНЫХ РИСКОВ СМЕРТНОСТИ НАСЕЛЕНИЯ. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ»

(утв. Минздравом РФ 22.01.2001 N 11-3/25-09)

Источник

4. Аппроксимация

В главе 3 была рассмотрена задача интерполяции, которая заключается в определении промежуточных значений функции по известному дискретному набору значений функции. Аппроксимация – это определение параметров аналитической функции, описывающей набор точек, полученных в результате эксперимента.

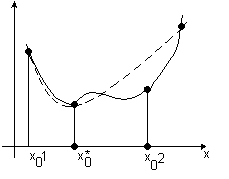
4.1. Задача аппроксимации

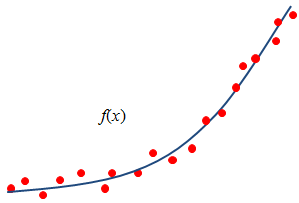
Предположим, имеется набор из n точек (x_i y_i), полученных в результате эксперимента, и необходимо аппроксимировать (описать) эти данные некоторой функцией f(x). Если исходные данные были получены с высокой точностью и количество точек не очень большое, то можно аппроксимировать данные функцией, которая проходит через все узловые точки. На практике экспериментально полученные данные всегда обладают погрешностью, часто довольно значительной, тогда при аппроксимации можно провести кривую таким образом, чтобы ее отклонение от всех точек было минимальным, но при этом она не обязательно будет проходить через каждую точку (рис.4.1). Такая аппроксимация сгладит погрешность первоначальных данных.

y₁	x₁
y₂	x₂
…	…
y_i	x_i
…	…
y_n	x_n

Рис.4.1. Задача аппроксимации

Представим аппроксимирующую функцию в виде суммы произведений коэффициентов с₀, с₁, …, с_m и базисных функций g₀, g₁, …, g_m:

, (4. 1)

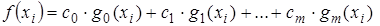
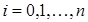
Выбор базисных функций, то есть зависимости, которой можно описать реальные данные – это отдельная задача, часто решаемая методом проб и последовательных приближений. В этом случае исходные данные, представленные в графической форме (семейства точек или кривые), сопоставляются с семейством графиков ряда типовых функций, используемых обычно для целей аппроксимации. Однако во многих случаях базисная функция известна, и требуется только найти ее коэффициенты.

Во многих случаях в качестве базисной функции выбирают степенной полином:

, (4.2)

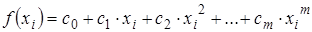
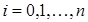
4.2. Система линейных алгебраических уравнений (СЛАУ)

Для определения неизвестных коэффициентов составим систему линейных уравнений. В общем случае система линейных алгебраических уравнений (СЛАУ) – это система из m линейных алгебраических уравнений с n неизвестными:

(4. 3)

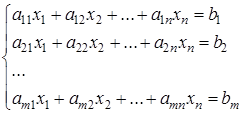
Систему линейных алгебраических уравнений можно записать в матричной форме:

(4.4)

(4.5)

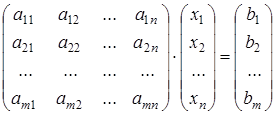
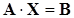
где A – матрица системы, X – столбец неизвестных, B – столбец свободных членов:

, , (4.6)

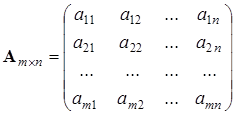
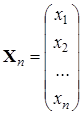
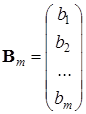
Решение системы линейных алгебраических уравнений сводиться к нахождению значений элементов столбца неизвестных X (корней системы) по известным A и B. Необходимым и достаточным условием существования единственного решения системы линейных алгебраических уравнений является условие 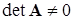, то есть определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной, и при этом СЛАУ либо не имеет решения, либо имеет бесчисленное множество решений.

Если матрица системы квадратная, и ее определитель не равен нулю, систему можно решить одним из следующих методов.

Метод Крамера

При небольшой размерности системы m для решения часто используют метод Крамера:

(4.7)

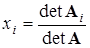
где 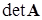– определитель матрицы системы, – определитель матрицы системы, где вместо i-го столбца стоит столбец правых частей.

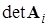
Для больших матриц решение методом Крамера является слишком долгим и трудоемким.

Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных, когда система уравнений (матрица A) приводится к равносильной системе треугольного вида (прямой ход метода Гаусса). Затем из полученной треугольной матрицы последовательно, начиная с последних по номеру, находятся все переменные системы (обратный ход метода Гаусса).

Метод обратной матрицы

Если 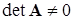, то существует обратная матрица . Тогда решение СЛАУ можно записать в виде:

(4.8)

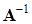
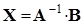
То есть, решение СЛАУ можно свести к умножению известной обратной матрицы на вектор правых частей. Нахождение обратной матрицы – трудоемкая операция, однако, при наличии вычислительных библиотек, предоставляющих вычисление обратной матрицы (иногда несколькими способами), такой вариант может быть менее сложен и более эффективен для самостоятельной реализации.

4.3. Пример использование СЛАУ для решения задачи аппроксимации

Систему линейных алгебраических уравнений можно применить и для решения задачи аппроксимации. Например, аппроксимируем n имеющихся точек (x_i y_i) параболой:

(4.9)

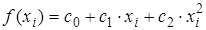
Тогда в столбец неизвестных можно записать искомые коэффициенты с₀, с₁, с₂, в столбец свободных членов – известные значения y₀,…, y_n, а в матрицу системы – вычисленные значения для каждого y_i при каждом коэффициенте с₀, с₁, с₂:

, , (4.10)

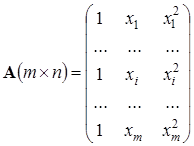
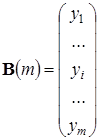
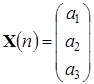
4.4. Метод наименьших квадратов (МНК)

Для переопределенных СЛАУ (количество уравнений больше количества неизвестных m > n) система не имеет единственного точного решения, но можно найти “оптимальный” вектор X. В этом случаем для решения СЛАУ используется метод наименьших квадратов (МНК). При помощи этого метода коэффициенты аппроксимирующей функции вычисляются таким образом, чтобы среднеквадратичное отклонение экспериментальных данных от найденной аппроксимирующей функции (сумма квадратов отклонений между векторами 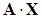и уравнения (4.5)) было наименьшим:

, где (4.11)

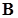
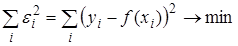
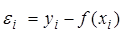
Для вывода решения системы линейных уравнений методом наименьших квадратов перепишем выражение (4.5), с добавлением вектора погрешности :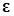

(4.12)

(4.13)

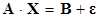
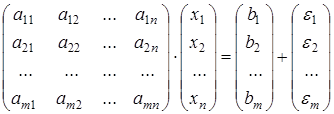
Теперь задача сводится к минимизации квадрата нормы вектора погрешности :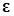

(4.14)

(4.15)

(4.16)

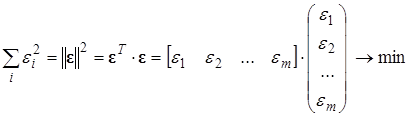
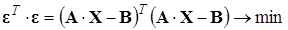
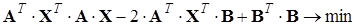
Для нахождения минимума необходимо вычислить частную производную по X уравнения (4.16) и приравнять ее к 0:

(4.17)

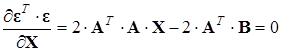
Отсюда находим значение вектора X:

(4.18)

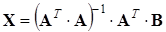
Таким образом, метод наименьших квадратов сводится к нахождению обратной матрицы.

Взвешенный метод наименьших квадратов

Если в полученных экспериментально данных разные измерения (точки) имеют разные погрешности, можно использовать взвешенный метод наименьших квадратов. Во взвешенном МНК разные уравнения системы (разные точки экспериментально полученных данных) получают разный вес w_i, обычно пропорциональный погрешности каждой точки 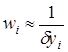. Взвешенный метод наименьших квадратов можно записать в матричном виде:

(4.19)

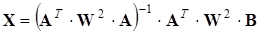
где W — диагональная матрица весов:

(4.20)

Источник

аппроксимация

Смотреть что такое «аппроксимация» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

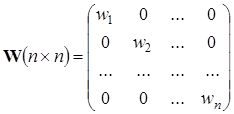
АППРОКСИМАЦИЯ

При выполнении определенных условий f(x) можно аппроксимировать конечной суммой ряда Тейлора или Фурье или конечными суммами других рядов. Типичным примером использования А. в геологии является решение задач по расчету тренда. См. Тренд-анализ.

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

Аппроксимация и интерполяция данных. Основные определения

Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Например: зависимость числа оборотов двигателя от нагрузки, т.е. n=f(Мкр.); зависимость силы резания при обработке детали на металлорежущем станке от глубины резания, т.е. P=f(t), и т.д.

Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости в виде функции n=f(Мкр.), P=f(t), y=f(t).

Однако на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, измеряются значения параметров на выходе системы. Результаты измерений заносятся в таблицу.

Таким образом, в результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию.

Далее с этой табличной функцией необходимо вести научно-исследовательские расчеты. Например, необходимо проинтегрировать или продифференцировать табличную функцию и т.д.

При такой постановке задачи моделирования нужно заменить табличную функцию аналитической. Для этой цели используются методы аппроксимации и интерполяции.

Аппроксимация – это замена исходной функции f(x) функцией φ(x) так, чтобы отклонение f(x) от φ(x) в заданной области было наименьшим. Функция φ(x) называется аппроксимирующей.

Если исходная функция f(x) задана таблично (дискретным набором точек), то аппроксимация называется дискретной. Если исходная функция f(x) задана аналитически (на отрезке), то аппроксимация называется непрерывной или интегральной.

Интерполяция – это замена исходной функции f(x) функцией φ(x) так, чтобы φ(x) точно проходила через точки исходной функции f(x).

Интерполяция еще называется точечной аппроксимацией.

Точки исходной функции f(x) называются узлами интерполяции.

Для интерполирующей функции справедливо

Экстраполяцией называется аппроксимация вне заданной области определения исходной функции, т.е.

Найдя интерполяционную функцию, мы можем вычислить ее значения между узлами интерполяции, а также определить значение функции за пределами заданного интервала (провести экстраполяцию).

Основной мерой отклонения функции y(x) от функции f(x) при аппроксимации является величина, равная сумме квадратов разностей между значениями аппроксимирующей и исходной функций

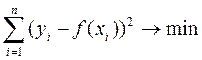Простейшими видами интерполяции является линейная и квадратичная.

При линейной интерполяции точки заданной функции соединяются линейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках. В качестве уравнения интерполяционного многочлена используются уравнения прямой, проходящей через две точки.

При квадратичной интерполяции в качестве приближающей функции, соединяющей соседние точки, принимается квадратный трехчлен. Такая интерполяция называется параболической.

Распространенным видом интерполяции является интерполяция с использованием кубических сплайн-функций.

Сплайн представляет собой модель гибкого тонкого стержня из упругого материала, закрепленного в двух соседних узлах интерполяции с заданными углами наклона α и β так, чтобы потенциальная энергия стержня была минимальна.

Интерполяция может выполняться с помощью многочленов Ньютона, Эрмита, Лагранжа и т.д.

Наиболее известными методами аппроксимации являются метод наименьших квадратов, метод многочленов Чебышева, рядов Тейлор и т.д.

При решении задач аппроксимации часто используются функции регрессии.

Регрессия – представление совокупности данных некоторой функцией f(x).

Задачей регрессии является вычисление параметров функции f(x) таким образом, чтобы функция приближала последовательность исходных точек с наименьшей погрешностью. При этом функция f(x) называется уравнением регрессии.

При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки.

Источник

Аппроксимация экспериментальных данных

Вы будете перенаправлены на Автор24

Аппроксимация экспериментальных данных — это научная методика, состоящая в замене одних объектов другими, в определенном смысле близкими к исходным данным, но более простыми.

Введение

Сегодня проблема аппроксимации считается актуальной темой фактически для любого технического исследования. От выбора типа аппроксимации в значительной мере зависит набор количественных характеристик и качественных свойств отображения исследуемых объектов.

Аппроксимацией является замена одних математи¬ческих объектов другими, в том или ином смысле, являющимися приближенными к исходным. Аппрок¬симация предоставляет возможность исследования числовых характеристик или качественных свойства объекта, путем сведения задачи к исследованию более простых или более удобных объектов (к примеру, та¬ких, у которых характеристики можно легко вычислить или свойства которых уже были извест¬ны ранее).

Приближением является аналог аппроксимации, термин «приближение» может иногда употребляться в смысле приближающего объекта. Приближением функций является определение для данной функции f функции g из некоторого определенного класса (к примеру, среди алгебраических многочленов требуемой степени), которая в некотором смысле будет близкой к f, то есть, дающей ее приближенное представление.

Моделью может быть любой образ какого-нибудь объекта, процесса или явления («оригинала» этой модели), применяемый как его «заместитель» или «представитель». Математической моделью является приближен¬ное описание какого-нибудь класса явлений окружающей действительности, которое выражено при помощи ма¬тематических символов. Физической моделью является приближенное описание определенного объекта или явления при помощи образа, который имеет такую же физическую природу.

Одним из главных этапов исследования явления при помощи его математической модели считается определение того факта, способна ли удовлетворить сформированная гипотетическая модель критериям практики, то есть, осуществляется выяснение вопроса о том, можно ли согласовать итоги наблюдений с теоретическими постулатами модели в границах точности наблюдений. Это означает, что требуется проверка на адекватность (то есть, наличие соответствия свойствам реального объекта) дан¬ной математической модели. При этом точность модели, обязана быть больше точности наблюдений, то есть, ошибка модели обязана быть меньше ошибки наблюдений.

Готовые работы на аналогичную тему

Адекватностью является соответствие, верность, точность. Точностью измерения является характеристика измерения, которая отражает уровень близости его результатов к фактическому значению измеряемой величины.

Аппроксимация экспериментальных данных

Аппроксимация условно может быть поделена на следующие виды:

Строгая теория математической аппроксимации состоит из следующих ме¬тодов аппроксимации:

Менее строгой аппроксимацией является физическая, то есть, техническая аппроксимация или математическая модель физического явления, процесса (физической модели), техниче¬ского устройства (его характеристик), сигнала (его параметров), среды, материи и тому подобное. Физическая (техническая) аппроксимация состоит из множества методов ап¬проксимации и аппроксимирующих функций, которые следует выбрать согласно конкретно по¬ставленной физической (технической) задаче.

То есть, при помощи физической (технической) аппроксимации может оператив¬но решаться обширный круг задач, являющихся актуальными на текущий момент времени, связанных с конкретными проблемами и вопросами прикладного (технического) характера. Строгая теория математической аппроксимации построена как фундаментальная, глобальная тео¬рия аппроксимации, которая, по сути, может и не помочь в решении повседневных прикладных практических задач. Это может случиться по причине либо потери с течением вре¬мени актуальности решаемой задачи, либо из-за сложности теории (аппроксимирующей функции), либо большого числа коэффициентов аппроксимации.

Приведем пример, который поясняет всю важность как технической аппроксимации, так и строгой математической теории. Если проследить процесс создания теории теплового излучения, то можно увидеть следующую очередность событий:

Необходимо заметить, что законы Стефана-Больцмана, Вина, Рэлея-Джинса являются частными случаями закона излучения Планка.

На рисунке ниже представлена классификация методов аппроксимации экспериментальных данных и формирования моделей:

Рисунок 1. Классификация методов аппроксимации экспериментальных данных и формирования моделей. Автор24 — интернет-биржа студенческих работ

Представленный выше путь развития физической теории теплового излучения является ни чем иным, как методом индукции, то есть, одним из типов умо¬заключения и методом исследования. Умозаключением является переход от отдельных фактов, то есть, частных случаев, к определенной гипотезе, то есть, общему утверждению или общим положениям.

Известен и иной, являющийся конкурирующим метод исследования, а именно, это дедукция, то есть, один из главных методов рассуждения (умозаключения) и методик исследования.

Нужны еще материалы по теме статьи?

Воспользуйся новым поиском!

Найди больше статей и в один клик создай свой список литературы по ГОСТу

Источник

Значение слова «аппроксимировать»

аппроксими́ровать

1. матем. производить аппроксимацию; заменять близким, приблизительно равным ◆ При проведении любых измерений в соответствии с центральными предельными теоремами теории вероятностей принято аппроксимировать распределения результатов гладкими кривыми, монотонно убывающими от экстремума (среднего арифметического измерений, математического ожидания). Симон Штоль, «Макроскопические флуктуации — возможное следствие флуктуации пространства-времени. (Арифметические и космофизические аспекты)», 2000 г. // «Российский химический журнал» (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова утя (существительное):

Источник

Линейная аппроксимация

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию ).

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:

Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

Источник

Электронная библиотека

Аппроксимацией (приближением) функции называется нахождение такой функции (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций и могут быть различные.

Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяций) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.

Рис. 3.6 Метод Лагранжа

Близость исходной и аппроксимирующей функций определяется числовой мерой

— критерием аппроксимации (близости). Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от «экспериментальных» (т.е. заданных), — критерий близости в заданных точках:

Здесь у_i — заданные табличные значения функции; у_i расч — расчетные значения по аппроксимирующей функции; b_i — весовые коэффициенты, учитывающие относительную важность i-и точки (увеличение b,. приводит при стремлении уменьшить R к уменьшению, прежде всего отклонения в i—й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).

Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.

Другим распространенным критерием близости является следующий:

Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.

Выделяют две основные задачи:

1) получение аппроксимирующей функции, описывающей имеющиеся данные, с погрешностью не хуже заданной;

2) получение аппроксимирующей функции заданной структуры с наилучшей возможной погрешностью.

Чаще всего первая задача сводится ко второй перебором различных аппроксимирующих функций и последующим выбором наилучшей.

Метод наименьших квадратов

Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и расчетных значений. При заданной структуре аппроксимирующей функции у_i расч (х) необходимо таким образом подобрать параметры этой функции, чтобы получить наименьшее значение критерия близости, т.е. наилучшую аппроксимацию. Рассмотрим путь нахождения этих параметров на примере полиномиальной функции одной переменной:

Запишем выражение критерия аппроксимации при b_i =1 (i=1, 2,…, n) для полиномиального у_i расч (х):

Искомые переменные а_j можно найти из необходимого условия минимума R по этим переменным, т.е. dR / dа_р = 0 (для _р =0, 1,2,…,k). Продифференцируем по а_р (р — текущий индекс):

После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим

Перепишем последние равенства

Получилась система n+1 уравнений с таким же количеством неизвестных а_j, причем линейная относительно этих переменных. Эта система называется системой нормальных уравнений. Из ее решения находятся параметры а_j аппроксимирующей функции, обеспечивающие minR, т.е. наилучшее возможное квадратичное приближение. Зная коэффициенты, можно (если нужно) вычислить и величину R (например, для сравнения различных аппроксимирующих функций). Следует помнить, что при изменении даже одного значения исходных данных (или пары значений х_i, у_i, или одного из них) все коэффициенты изменят в общем случае свои значения, так как они полностью определяются исходными данными. Поэтому при повторении аппроксимации с несколько изменившимися данными (например, вследствие погрешностей измерения, помех, влияния неучтенных факторов и т.п.) получится другая аппроксимирующая функция, отличающаяся коэффициентами. Обратим внимание на то, что коэффициенты а_j полинома находятся из решения системы уравнений, т.е. они связаны между собой. Это приводит к тому, что если какой-то коэффициент вследствие его малости захочется отбросить, придется пересчитывать заново оставшиеся. Можно рассчитать количественные оценки тесноты связи коэффициентов. Существует специальная теория планирования экспериментов, которая

позволяет обосновать и рассчитать значения х_i, используемые для аппроксимации, чтобы получить заданные свойства коэффициентов (несвязанность, минимальная дисперсия коэффициентов и т.д.) или аппроксимирующей функции (равная точность описания реальной зависимости в различных направлениях, минимальная дисперсия предсказания значения функции и т.д.).

Рис. 3.7 Влияние степени аппроксимирующего полинома М на точность аппроксимации

В случае постановки другой задачи — найти аппроксимирующую функцию, обеспечивающую погрешность не хуже заданной, — необходимо подбирать и структуру этой функции. Эта задача значительно сложнее предыдущей (найти параметры аппроксимирующей функции заданной структуры, обеспечивающей наилучшую возможную погрешность) и решается в основном путем перебора различных функций и сравнения получающихся мер близости. Для примера на рис. 3.7 приведены для визуального сравнения исходная и аппроксимирующие функции с различной степенью полинома, т.е. функции с различной структурой. Не следует забывать, что с повышением точности аппроксимации растет и сложность функции (при полиномиальных аппроксимирующих функциях), что делает ее менее удобной при использовании.

Рассмотрим решение задачи аппроксимации и интерполяции с шумом в

программе MathCAD (рисунок 3.8).

Источник

Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

Аппроксимация функций, моделирующих сигналы

Сглаживание статистических данных или аппроксимация данных с учетом их статистических параметров относится к задачам регрессии, и рассматриваются в следующей теме. Как правило, при регрессионном анализе усреднение данных производится методом наименьших квадратов (МНК).

Все вышеперечисленные задачи относятся к задачам приближения сигналов и функций и имеют многовековую историю, в процессе которой сформировались классические математические методы аппроксимации, интерполяции, экстраполяции и регрессии функций. В рамках настоящего курса мы не будем углубляться в строгую математическую теорию этих операций. Все современные математические системы (Mathcad, MATLAB, Maple и пр.) имеют в своем составе универсальный аппарат выполнения таких операций, дающий пользователю возможность реализации любых практических задач по обработке данных без отвлечения на теоретические подробности их исполнения. В качестве основной математической системы для примеров использована система Mathcad.

Содержание

Приближение сигналов рядами Тейлора

Исторически разложение функций в ряд Тейлора явилось одним из первых методов приближения функций в окрестностях точек x 0 <\displaystyle x_<0>\,\!> :

Источник

Лекция 17. Приближение функций

Аппроксимация – замена одной функции f(x) другой, похожей функцией Q(x). Например, функцию, полученную экспериментально в виде таблицы или графика, надо записать в аналитическом виде, либо функцию, достаточно сложную нужно заменить похожей, но более простой.

Простейший способ аппроксимации – замена функции f(x) алгебраическим полиномом

Необходимо так подобрать коэффициенты в формуле (2.1), чтобы Q(x, c_j ) как можно меньше отличалась от f ( x ).

2.1 Меры погрешности аппроксимации

1. Равномерное приближение

a) точечная аппроксимация

Подберем коэффициенты с_j таким образом, чтобы R было минимальным:

Это есть минимаксный подход, который осуществляет равномерное приближение функций.

b) интегральная аппроксимация

Критерий (2.3) перепишется в виде:

2. Метод наименьших модулей

a) точечная аппроксимация

b) интегральная аппроксимация

3. Метод наименьших квадратов

Чаще всего при точечной аппроксимации используют меру

а коэффициенты с j ищут из условия

Это точечная квадратичная аппроксимация.

При интегральной аппроксимации

Описанный подход к задаче аппроксимации называется методом наименьших квадратов. Условия (2.9) и (2.10) геометрически означают: из всех кривых заданного вида выбирают ту, у которой сумма площадей квадратов отклонений – наименьшая.

2.2 Нахождение коэффициентов c_j при точечной аппроксимации методом наименьших квадратов

Пример: построить аппроксимирующую параболу для функции

Источник

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

Аппроксимация

Аппроксима́ция (от лат. proxima – ближайшая) или приближе́ние — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.

В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

Содержание

Остаточный член

Остаточный член — разность между заданной функцией и функцией её аппроксимирующей. Тем самым оценка остаточного члена является оценкой точности рассматриваемой аппроксимации. Этот термин применяется, например, в формуле ряда Тейлора.

Примеры

: неверное или отсутствующее изображение

Если функция будет использована только для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

Источник

АППРОКСИМАЦИЯ

замена одних математич. объектов другими, в том или ином смысле близкими к исходным. А. позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (напр., таких, характеристики к-рых легко вычисляются или свойства к-рых уже известны). В теории чисел изучаются диофантовы приближения, в частности приближения иррациональных чисел рациональными. В геометрии и топологии рассматриваются А. кривых, поверхностей, пространств и отображений. Нек-рые разделы математики в сущности целиком посвящены А., напр, теория приближения функций, численные методы анализа. БСЭ-3.

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

Источник

Значение слова аппроксимация

Аппроксимация в словаре кроссвордиста

аппроксимация

Аппроксимация Аппроксима́ция (от — ближайшая) или приближе́ние — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны).

, аппроксимирование ( лат. approximare приближаться) мат. приближенное выражение каких-л. величин (или геометрических объектов) через другие, более простые величины.

Новый словарь иностранных слов

Словарь русского языка Лопатина

Современный толковый словарь, БСЭ

Большая советская энциклопедия, БСЭ

Полный орфографический словарь русского языка

Если там затрагивался вопрос модификации общества, построение его на более разумных принципах, чем нынешняя псевдодемократия [4], то в этой книге вопрос ставится гораздо шире, а именно: что такое человек, как он развивался в этом качестве, к чему это привело и как выглядит аппроксимация этого развития.

Реально уход уже начался, просто из–за близости событий он не виден — это даже имеет научное название — аппроксимация близости.

Источник

Метод аппроксимации в Microsoft Excel

Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

Выполнение аппроксимации

Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

Но она может быть построена с применением одного из пяти видов аппроксимации:

Рассмотрим каждый из вариантов более подробно в отдельности.

Способ 1: линейное сглаживание

Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.

Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.

Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.

Сглаживание, которое используется в данном случае, описывается следующей формулой:

В конкретно нашем случае формула принимает такой вид:

Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.

Способ 2: экспоненциальная аппроксимация

Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.

Общий вид функции сглаживания при этом такой:

где e – это основание натурального логарифма.

В конкретно нашем случае формула приняла следующую форму:

Способ 3: логарифмическое сглаживание

Теперь настала очередь рассмотреть метод логарифмической аппроксимации.

В общем виде формула сглаживания выглядит так:

где ln – это величина натурального логарифма. Отсюда и наименование метода.

В нашем случае формула принимает следующий вид:

Способ 4: полиномиальное сглаживание

Настал черед рассмотреть метод полиномиального сглаживания.

Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:

В нашем случае формула приняла такой вид:

Формула, которая описывает данный тип сглаживания, приняла следующий вид:

Способ 5: степенное сглаживание

В завершении рассмотрим метод степенной аппроксимации в Excel.

Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.

Общая формула, описывающая данный метод имеет такой вид:

В конкретно нашем случае она выглядит так:

Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

Источник

Аппроксимация функций

Смотреть что такое «Аппроксимация функций» в других словарях:

Аппроксимация — В Викисловаре есть статья «аппроксимация» Аппроксимация, или приближение научный метод, состоя … Википедия

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА РАЗНОСТНЫМ — приближение дифференциального оператора таким зависящим от параметра оператором, результат применения к рого к функции определяется ее значениями на нек ром дискретном множестве точек сетке, уточняющееся при стремлении параметра (шага сетки) к… … Математическая энциклопедия

Аппроксимация Паде — Содержание 1 История 2 Определение 3 Таблица Паде … Википедия

аппроксимация — (от лат. approximo приближаюсь), замена одних математических объектов (например, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (например, кривых линий близкими к ним ломаными). * * * АППРОКСИМАЦИЯ… … Энциклопедический словарь

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОЙ КРАЕВОЙ ЗАДАЧИ РАЗНОСТНОЙ — приближение дифференциального уравнения и краевых условий системой конечных (обычно алгебраических) уравнений относительно значений искомой функции на нек рой сетке, к рое уточняется при стремлении параметра разностной задачи (шага сетки) к нулю … Математическая энциклопедия

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РАЗНОСТНЫМ — приближение дифференциального уравнения системой алгебраич. уравнений относительно значений искомых функций на нек рой сетке, к рое уточняется при стремлении параметра (шага сетки) к нулю. Пусть нек рый дифференциальный оператор, а нек рый… … Математическая энциклопедия

Аппроксимация — (от лат. approximo приближаюсь) замена одних математических объектов другими, в том или ином смысле близкими к исходным. А. позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более… … Большая советская энциклопедия

Источник

Аппроксимация

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании.

Прострáнством называется математическое множество, имеющее структуру, определяемую аксиоматикой свойств его элементов (например, точек в геометрии, векторов в линейной алгебре, событий в теории вероятностей и так далее).Подмножество пространства называется «подпространством», если структура пространства индуцирует на этом подмножестве структуру такого же типа (точное определение зависит от типа пространства).

О дискретном эквиваленте преобразования Лапласа см. Z-преобразование.В математике дискретный оператор Лапласа — аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа (имеющего конечное число вершин и рёбер) дискретный оператор Лапласа имеет более общее название: матрица Лапласа.

Источник

Значение слова аппроксимация

аппроксимация в словаре кроссвордиста

аппроксимация

Энциклопедический словарь, 1998 г.

Большая Советская Энциклопедия

Имена, названия, словосочетания и фразы содержащие «аппроксимация»:

Википедия

Имена, названия, словосочетания и фразы содержащие «аппроксимация»:

Примеры употребления слова аппроксимация в литературе.

Суть аппроксимации понятием заключается в том, что символ, имея смысл и значение, является экспликатом и экспликандуумом, как было представлено выше, вторая природа, рассмотренная в качестве триады математическое понятие множества есть первая указанная триада, дескрипция проблемы выполнимости формул подстановок.

Классическая теория вычисления, которая в течение полувека оставалась неоспоримым основанием вычисления, сейчас устарела, превратившись разве что, как и остальная классическая физика, в схему аппроксимации.

Если в ясный день отключить осветительные дуги, серая аппроксимация солнечного света будет фильтроваться через слои акриопластика: пейзаж, напоминающий тюремные наброски Джованни Пиранези.

Алеф это аппроксимация, близкое подобие матрицы, говорит он, что-то вроде модели киберпространства.

Излюбленная конструктом аппроксимация смеха заскребла по нервам Кейса, как тупая бритва.

Мы можем сделать это ради тренировки, развлечения или аппроксимации, потому что осуществить истинную передачу слишком сложно или слишком дорого.

Он говорит нам, что действительные законы физики, по крайней мере, до сих пор, поддаются последовательной аппроксимации с помощью теорий, дающих лучшие объяснения и предсказания, и что задача открытия каждой теории при наличии предыдущей легко решалась с помощью вычислений при наличии уже известных законов и уже имеющейся технологии.

Источник: библиотека Максима Мошкова

Транслитерация: approksimatsiya
Задом наперед читается как: яицамискорппа
Аппроксимация состоит из 13 букв

Источник

Аппроксимация что это

Значение слова «аппроксимация»

аппроксима́ция

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

Что такое аппроксимация

Аппроксимация в математике — это …

Применение термина «аппроксимация» в иных областях

Краткое резюме

Комментарии и отзывы (2)

Аппроксимация

Остаточный член

Примеры

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

Аппроксимация

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

АППРОКСИМАЦИЯ

Найдено 1 изображение:

4. Аппроксимация

4.1. Задача аппроксимации

4.2. Система линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Метод Гаусса

Метод обратной матрицы

4.3. Пример использование СЛАУ для решения задачи аппроксимации

4.4. Метод наименьших квадратов (МНК)

Взвешенный метод наименьших квадратов

аппроксимация

Смотреть что такое «аппроксимация» в других словарях:

Аппроксимация

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

Аппроксимация и интерполяция данных. Основные определения

Аппроксимация экспериментальных данных

Введение

Готовые работы на аналогичную тему

Аппроксимация экспериментальных данных

Значение слова «аппроксимировать»

аппроксими́ровать

Делаем Карту слов лучше вместе

Линейная аппроксимация

Аппроксимация линейной функцией

Пример реализации

Построение графика функции

Аппроксимация с фиксированной точкой пересечения с осью y

Электронная библиотека

Национальная библиотека им. Н. Э. Баумана Bauman National Library

Персональные инструменты

Аппроксимация функций, моделирующих сигналы

Содержание

Приближение сигналов рядами Тейлора

Лекция 17. Приближение функций

2.1 Меры погрешности аппроксимации

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

Аппроксимация

Содержание

Остаточный член

Примеры

АППРОКСИМАЦИЯ

Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:

Значение слова аппроксимация

Аппроксимация в словаре кроссвордиста

аппроксимация

Метод аппроксимации в Microsoft Excel

Выполнение аппроксимации

Способ 1: линейное сглаживание

Способ 2: экспоненциальная аппроксимация

Способ 3: логарифмическое сглаживание

Способ 4: полиномиальное сглаживание

Способ 5: степенное сглаживание

Национальная библиотека им. Н. Э. Баумана
Bauman National Library