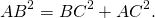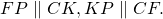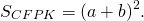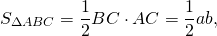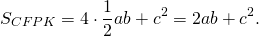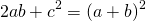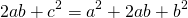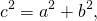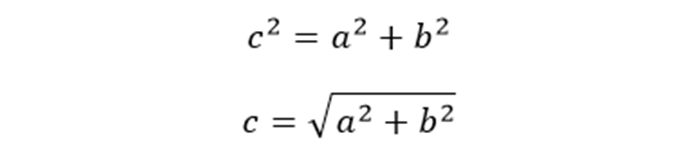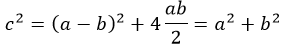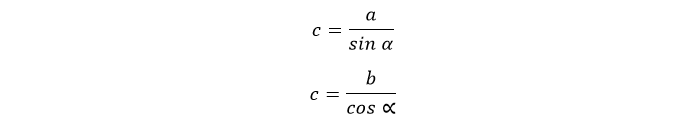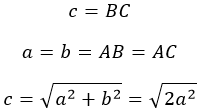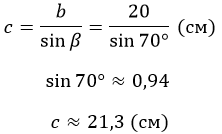Чему равен квадрат гипотенузы
Чему равен квадрат гипотенузы
Чему равен квадрат гипотенузы?
Чему равен квадрат гипотенузы.
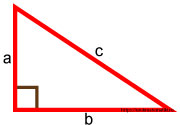
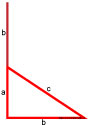
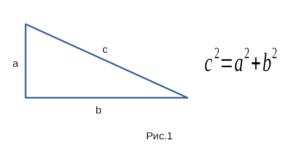
Простое школьное правило для прямоугольного треугольника, а точнее теорема Пифагора, где самая большая сторона, расположенная напротив прямого угла называется гипотенузой, а две остальные катетами.
Квадрат гипотенузы равен сумме квадратов катетов.
Теорема о квадрате гипотенузы принадлежит великому древнегреческому философу и мудрецу, математику Пифагору. Суть её в том, что
Квадрат гипотенузы равен сумме квадратов катетов.
Геометрия, самые первые уроки. Квадрат гипотенузы равен сумме квадратов катетов. Это должен знать любой школьник. А более менее грамотный должен уметь и доказать эту теорему Пифагора, хотя бы одним из многочисленных способов.
Так, попробую вспомнить свои школьный знания.
Квадрат гипотенузы равен сумме квадратов катетов в прямоугольном треугольнике. Вроде так)
Это теорема Пифагора, если я не ошибаюсь. Давно все это было.
Квадрат гипотенузы равен сумме квадратов катета c^2=a^2+b^2
Квадрат гипотенузы равен сумме квадратов катетов.
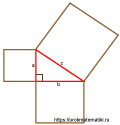
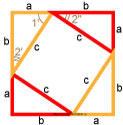
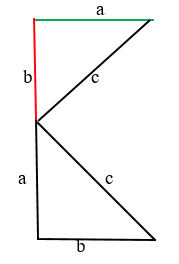
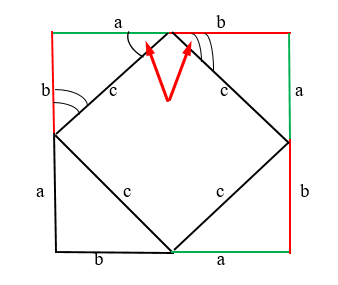
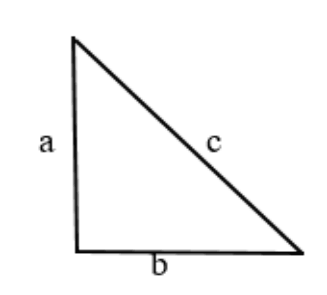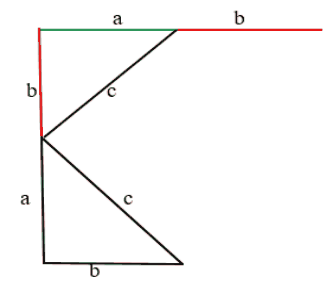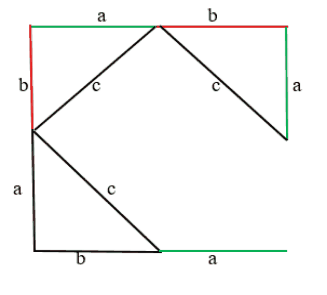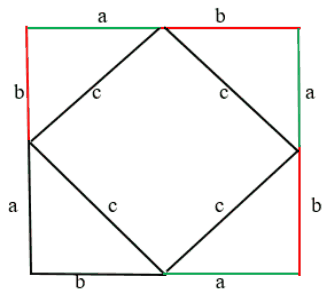
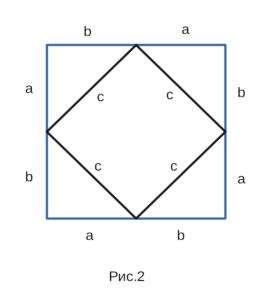
Нагляднее всего можно показать ответ на вопрос благодаря данному рисунку.
Таким образом, квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора
О чем эта статья:
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
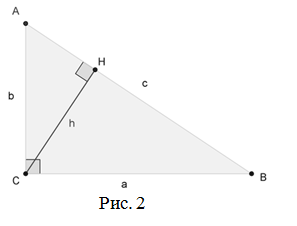
Дано: ∆ABC, в котором ∠C = 90º.
Пошаговое доказательство:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
a 2 + b 2 = c * AB
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
Пусть катеты a = 6 и b = 8.
Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
Ответ: треугольник не является прямоугольным.
Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру
Нужно доказать, что c² = a² + b²:
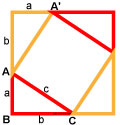
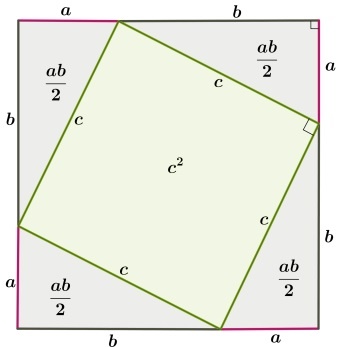
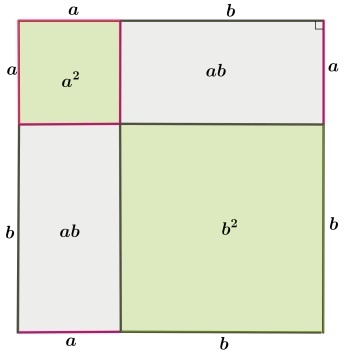
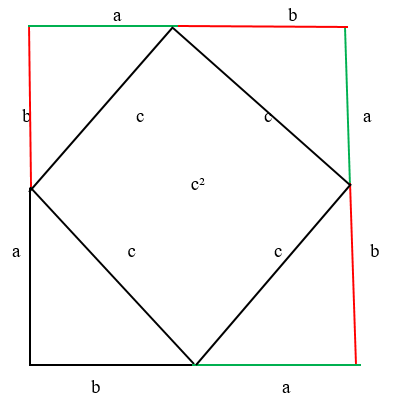
Это квадрат, в котором есть 4 одинаковых треугольника abc:
(a + b) (a + b) = c² + 2ab
a² + 2ab + b² = c² + 2ab
Что и требовалось доказать.
«Пифагоровы штаны на все стороны равны»
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
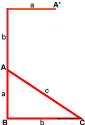
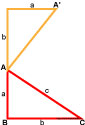
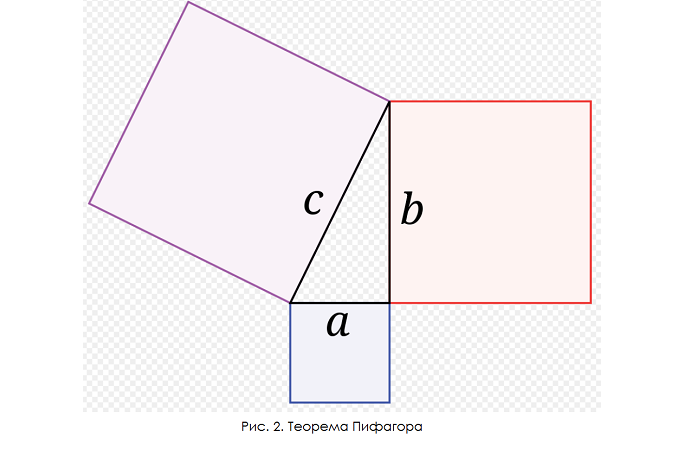
На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
Что и требовалось доказать.
Примеры
Задача 1
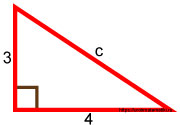
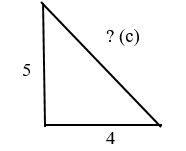
На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Подставить известные значения
Ответ: длина гипотенузы равна 5.
Задача 2
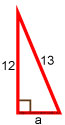
Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Подставить известные значения
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.
Теорема Пифагора: формула и доказательство
Теорема Пифагора гласит:
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
Формулы теоремы Пифагора
Доказательство теоремы Пифагора
Площадь прямоугольного треугольника вычисляется по формуле:
Для вычисления площади произвольного треугольника формула площади:
Потом приравниваем правые части обеих формул для площади треугольника:
2 ab = \left( (a+b)^ <2>-c^ <2>\right)
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b и c, такой, что
существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Значение теоремы в том, что с ее помощью можно доказать другие теоремы и решать задачи.
Дополнительный материал: Теорема о сумме углов треугольника
Теорема Пифагора
Формула теоремы Пифагора
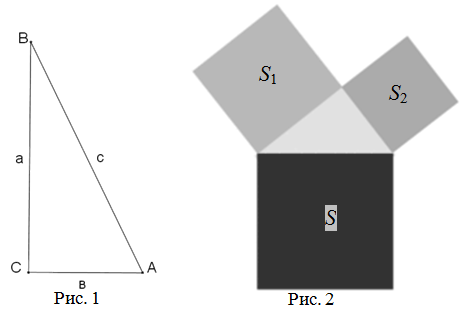
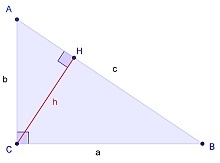
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):
Доказательство теоремы Пифагора
из подобия треугольников получаем, что
Отсюда имеем, что
$$a^<2>=c \cdot H B, b^<2>=c \cdot A H$$
Сложив полученные равенства, получаем
$$a^<2>+b^<2>=c \cdot H B+c \cdot A H$$
Что и требовалось доказать.
Геометрическая формулировка теоремы Пифагора
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 2):
Примеры решения задач
Отсюда получаем, что искомая гипотенуза
Ответ. 10 см
Задание. Найти площадь прямоугольного треугольника, если известно, что один из его катетов на 5 см больше другого, а гипотенуза равна 25 см.
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:
Согласно теореме Виета, получаем, что
Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть
Историческая справка
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Остались вопросы?
Здесь вы найдете ответы.
Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с прямыми углами, возведенное в квадратную степень, является величиной, равной сумме его катетов (а и b), каждый из которых также возведен в квадрат. Наглядно и с применением условных обозначений это выглядит так:
В теореме Пифагора говорится о том, что в треугольнике с прямыми углами сумма длин катетов, каждая из которых возведена в квадрат, равна длине его гипотенузы, также возведенной в квадратную степень.
При этом под гипотенузой понимается сторона, которая расположена противоположно прямому углу. Катетом считается одна из сторон, участвующих в образовании прямого угла.
Основание прямоугольного треугольника обозначим как Н. Из его вершины С проведем высоту на гипотенузу АВ. Получившийся в результате этого треугольник АСН является подобным треугольнику АВС по двум углам, равным 90º (∠ACB =∠CHA).
Подобными также являются треугольные фигуры АВС и СВН. Основанием их подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют общий угол, которым является ∠B.
Для продолжения доказательства теоремы Пифагора следует ввести дополнительные обозначения: BC = a, AC = b, AB = c.
На основании полученной ранее информации о подобии треугольников можно утверждать, что:
a/с = HB/a, b/с = AH/b.
Полученное равенство также позволяет сделать следующий вывод:
a2 = c * HB, b2 = c * AH.
На следующем этапе произведем сложение полученных ранее равенств:
a2 + b2 = c * HB + c * AH
Вынесем за скобки общий множитель во второй части равенства:
a2 + b2 = c * (HB + AH)
Теперь можно сократить Н в левой части равенства, в результате получим:
В приведенных выше обозначениях указано, что АВ = с. Это позволяет переписать равенство следующим образом:
a2 + b2 = c * c, или a2 + b2 = c2
Таким образом, теорема Пифагора доказана.
Согласно теореме Пифагора, длина гипотенузы прямоугольного треугольника, которая возведена в квадрат, равна сумме, полученной в результате сложения квадратов длин его катетов. Из этого следует, что:
Извлечем квадрат из обеих частей равенства, в итоге получим:
x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2
Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен 5 см, составляет 5√2, что равно примерно 7,07 см.
Теорема Пифагора не может быть применима к треугольнику с тупыми или острыми углами. Она выполняется только в случае прямоугольного треугольника.
Для треугольника с углом 90º справедливо утверждение о том, что длина его гипотенузы, возведенная во вторую степень, равна сумме длин его катетов, взятых в квадрат.
В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного треугольника, возведенных во вторую степень, равна квадрату длины его гипотенузы. В случае с треугольником, некоторые параметры которого приведены в задании, это утверждение выглядит следующим образом:
х² = 7²-6² = 49-36 = 13.
Для того чтобы найти значение х, нужно извлечь квадратный корень из числа 13:
Ответ: Длина второго катета прямоугольного треугольника равна корню квадратному из 13.
Для решения поставленной задачи следует воспользоваться теоремой Пифагора, которая говорит о том, что сумма длин катетов треугольника с прямым углом, возведенных в квадрат, равна длине его гипотенузы, также возведенной во вторую степень:
Теорема Пифагора может быть применима в данном случае по причине того, что образованная между двумя домами конструкция является прямоугольным треугольником. Зная о том, что сумма квадратов катетов в прямоугольном треугольнике равна длине его катета, возведенной в квадрат, можно вычислить длину неизвестного катета:
24 м – 16 м = 8 м.
Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это, можно применить теорему Пифагора для вычисления длины гипотенузы:
(16*16) + (8*8) = 256 + 64 = 320 м.
Осталось только извлечь квадратный корень из 320, для того чтобы узнать длину расстояния между крышами двух домов.
Ответ: Расстояние между крышами домов равно корню квадратному из 320.
Обозначим длину неизвестного катета как х. Зная то, что по теореме Пифагора длина гипотенузы прямоугольного треугольника, возведенная во вторую степень, равна сумме длин его катетов, которые также возведены в квадрат, можно выразить длину неизвестного катета следующим образом:
х² = 132 – 122 = 169 – 144 = 25
Теперь, для того чтобы узнать длину второго катета, необходимо извлечь квадратный корень из числа 25:
Ответ: длина второго катета прямоугольного треугольника равна 5 см.
Известно, что длина медианы (m), которая проведена к гипотенузе прямоугольного треугольника, равна ½ ее длины. Используя это, можно высчитать длину гипотенузы прямоугольного треугольника:
с = 2*m = 2*6,5 = 13 см.
Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного треугольника, можно вычислить, чему равен его второй катет. Для этого можно использовать теорему Пифагора, согласно которой:
Выражаем из записанного выше равенства длину неизвестного катета:
Из полученного числа нужно извлечь квадратный корень, для того чтобы узнать длину второго катета прямоугольного треугольника:
Ответ: Длина второго катета прямоугольного треугольника равна 12 см.
Равенство, указанное в задании, применимо к треугольнику с прямым углом, как гласит теорема Пифагора.
Каждая из сторон треугольника может быть обозначена прописной буквой, которая соответствует строчной букве, обозначающей угол треугольника, расположенный противоположно этой стороне. На основании этого можно сделать вывод о том, что искомый треугольник является прямоугольным и имеет гипотенузу f и катеты a и b:
Ответ: имеется треугольник АDF с прямым углом F.
Теорема, которая является обратной теореме Пифагора, существует. Согласно этой теореме, треугольник считается прямоугольным в том случае, если длина его большей стороны, возведенная в квадратную степень, равна сумме длин двух других его сторон, которые также возведены в квадратную степень.
Для начала следует провести высоту (h) к основанию равнобедренного треугольника. Данная высота, проведенная к основанию, в случае с равнобедренным треугольником является медианой.
Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет равна:
Площадь (S) треугольника рассчитывается путем деления на число, полученное в результате умножения длины высоты на длину основания треугольника:
S = ½*10,5√15 см*51 см = 267,75√15 см².
Ответ: Площадь треугольника равна 267,75√15 см².
В равностороннем треугольнике высота (h), проведенная к его основанию, является также его биссектрисой и медианой. Она делит равносторонний треугольник на две части, которые являются равными треугольниками с прямым углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный вопрос следует применить теорему Пифагора:
Обозначим меньший из катетов как х. Тогда другой катет, длина которого в два раза больше, будет обозначен как 2х. Если в случае с прямоугольным треугольником, длина гипотенузы которого равна √15, применить теорему Пифагора, то она будет выглядеть следующим образом:
После раскрытия скобок в уравнении получаем следующее равенство:
Складываем слагаемые в первой части и получаем:
Сокращаем обе части уравнения на 5, и в итоге получается, что:
Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.
Если обозначить длину неизвестного катета через х, то гипотенуза будет равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для данного треугольника:
После сокращений получается следующее равенство:
Теперь можно найти значение х:
Длина второго катета равна 80 см.
Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180 см, можно вычислить длину гипотенузы:
Ответ: Длина гипотенузы равна 100 см.
АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см. Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются неизвестными величинами. Длину ВС можно вычислить по следующей формуле:
Произведем перенос высоты:
Тогда получаем, что:
Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.
Теорема Пифагора
Теорема Пифагора в геометрии важна не меньше, чем таблица умножения в арифметике. Решение многих геометрических задач (как в планиметрии, так и в стереометрии), сводится к рассмотрению прямоугольных треугольников и применению этой замечательной теоремы.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Существует множество разнообразных способов доказательства теоремы Пифагора. Ограничимся лишь одним из них.

Пусть BC=a, AC=b, AB=c.
На гипотенузе AB построим квадрат со стороной c.

на продолжении стороны BC — отрезок BK, BK=b.
CF=AF+AC=a+b, CK=BC+BK=a+b, то есть CF=CK=a+b.
Через точки F и K проведём прямые, параллельные катетам:
Четырёхугольник CFPK — параллелограмм (по определению).
А так как ∠C=90º и CF=CK, то CFPK — квадрат со стороной a+b.
Так как площадь квадрата равна квадрату его стороны, то
С другой стороны, площадь CFPK равна сумме площадей четырёх прямоугольных треугольников с катетами b и c и квадрата со стороной c.
Площадь прямоугольного треугольника равны половине произведения его катетов:
площадь квадрата со стороной c равна c².
Приравняем правые части формул площади CFPK:
После упрощения получаем
Теорема Пифагора
Теорема Пифагора — пожалуй, одна из самых известных теорем в математике вообще и геометрии в частности. На самом деле несмотря на то, что она названа именем Пифагора, она была известна еще за тысячу лет до него.
Если вы построите вместо квадратов любые подобные фигуры, допустим полуокружности, то сумма этих площадей, построенных на катетах, все равно будет равняться площади фигуры, построенной на гипотенузе.
Доказательство теоремы Пифагора
На сегодняшний день известно более 200 различных доказательств теоремы Пифагора. Мы воспользуемся одним из них.
Преобразовав описанное выше в формулу, получаем:
a + b 2 = 4 · 1 2 a b + c 2
Раскроем формулу квадрата суммы:
a 2 + b 2 + 2 a b = 2 a b + c 2
a 2 + b 2 + 2 a b = 2 a b + c 2
Мы доказали теорему Пифагора.
Задачи на тему «Теорема Пифагора»
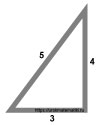
Египетский треугольник
Требуется найти его гипотенузу.
Решение:
Обозначим гипотенузу как c и воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
3 2 + 4 2 = c 2
9 + 16 = c 2
25 = c 2
c = 5
Пифагорова тройка
Требуется найти второй катет.
Обратите внимание, что в первом и втором примерах стороны треугольников получились целыми числами. Такие числа, которые удовлетворяют теореме Пифагора, называются пифагоровыми тройками.
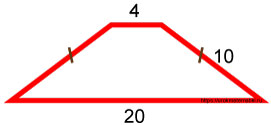
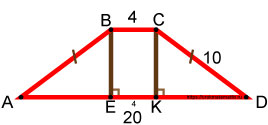
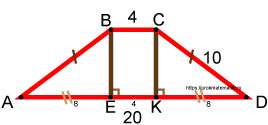
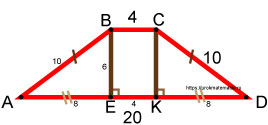
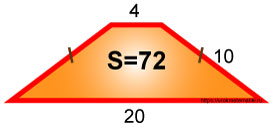
Равнобедренная трапеция
Так как наша трапеция равнобокая, то левый и правый треугольники равны между собой, т.к. имеют одинаковые катеты и одинаковые гипотенузы. По признакам равенства прямоугольных треугольников они равны. Это означает, что отрезки AE и KD равны между собой.
Применение теоремы Пифагора
Наиболее частое применение теоремы Пифагора можно увидеть в строительстве. В современные дальномеры встраивается функция, косвенно определяющая размеры стороны (треугольника) при измерении двух других сторон.
Рассмотрим два теоретических примера, когда необходимо произвести расчёт конструкции крыши, а в другом примере научимся позиционировать стены дома относительно друг друга под углом 90°.
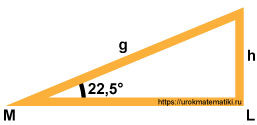
Расчет стропильной системы крыши
Задача крайне упрощённая для точных расчётов стропильной системы крыши, но достаточно понятная, чтобы донести принципы расчёта по теореме Пифагора.
Требуется найти длину стропила ( g ) и высоту стойки ( h ).
Теперь подставляем в формулу известные значения для определения высоты стойки ( h ) по теореме синусов:
sin 22,5° h = sin 67,5° ML
h = 5 · sin 22,5° sin 67,5° = 2.0710678118655
Также по теореме синусов можно найти и длину ( g ), но нас интересует теорема Пифагора.
Поэтому зная, что квадрат гипотенузы (в нашем случае это g ) равен сумме квадратов катетов (в нашем случае это h и расстояние между точками ML ), получаем:
Подставляя в формулу ранее вычисленные и известные значения, получаем:
Египетский треугольник
Ещё одним примером практического применения теоремы Пифагора в строительстве может служить использование египетского треугольника.
Соедините верёвку в треугольник, как показано на изображении, и натяните стороны полученного треугольника.
Угол между сторонами 3, 4 всегда будет равен 90°. По нему можно разметить стены или фундамент будущего дома.
Теорема Пифагора: квадрату гипотенузы равна сумма катетов, возведенных в квадрат
Каждый школьник знает, что всегда квадрат гипотенузы равен сумме катетов, каждый из которых возведен в квадрат. Эта утверждение носит название теоремы Пифагора. Она является одной из самых известных теорем тригонометрии и математики в целом. Рассмотрим ее подробнее.
Понятие о прямоугольном треугольнике
Перед тем, как переходить к рассмотрению теоремы Пифагора, в которой квадрат гипотенузы равен сумме катетов, которые возведены в квадрат, следует рассмотреть понятие и свойства прямоугольного треугольника, для которого справедлива теорема.

Сторону, которая лежит против прямого угла, принято называть гипотенузой. Две же другие стороны являются катетами треугольника, они могут быть равны между собой, а могут и отличаться. Из тригонометрии известно, что чем больше угол, против которого лежит сторона в треугольнике, тем больше длина этой стороны. Это означает, что в прямоугольном треугольнике гипотенуза (лежит против угла 90o) будет всегда больше любого из катетов (лежат против углов Понравилась статья? Поделись с друзьями:
Доказательства теоремы Пифагора
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Методом бесконечных малых
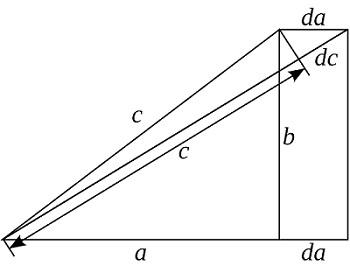
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
da/ca = c/a, b = const
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
c 2 = a 2 + const
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника.
Будет полезно сохранить таблицу Пифагора.
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
Или, иными словами:
Для всякой тройки положительных чисел a, b и c, такой, что

существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей, аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим
её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.


или 
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

треугольника так, как показано на рисунке
Четырёхугольник со сторонами c – квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b). Тогда для константы интегрирования получим:
Теорема Пифагора
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.
История теоремы
Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.
Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.
Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.
Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Теорема Пифагора, формула
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (
). Это одна из основополагающих теорем эвклидовой геометрии.
Формула:
Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.
Доказательство теоремы методом площадей: 1 способ
Докажем, что .
Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.
Получается такой же треугольник, только перевёрнутый.
Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре =
, так как все 4 гипотенузы со стороной
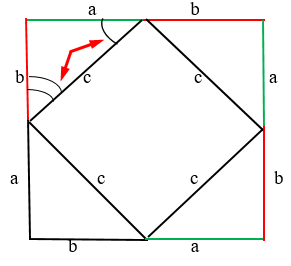
. Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:
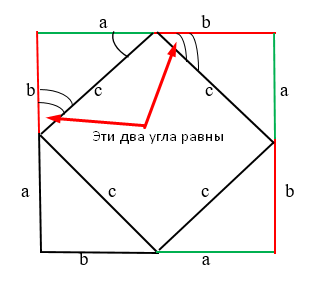
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:
Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.
Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.
Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.
Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной
– это будет квадрат его стороны. То есть
. Этот квадрат состоит из четырёх одинаковых треугольников.
И это значит, что мы доказали теорему Пифагора.
ВАЖНО. Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.
Примеры решения задач
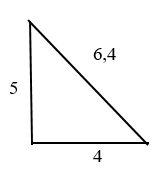
Дано: прямоугольный треугольник с катетами 4 и 5.
Найдите гипотенузу. Пока её обозначим “с”
Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае –
.
Воспользуемся теоремой Пифагора:
Итак, , а
. Катеты в сумме получают 41.
Тогда . То есть квадрат гипотенузы равен 41.
Квадрат числа 41 = 6,4.
Мы нашли гипотенузу.
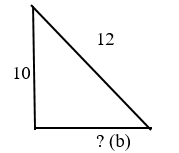
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10
Найдите второй катет.
Обозначим неизвестный катет – b.
Воспользуемся теоремой Пифагора:
, а
Находим
Если , тогда просто
Второй катет (b) равен 6,6.
Заключение
Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.
Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).
Средняя оценка 4.3 / 5. Количество оценок: 4
Теорема Пифагора
Теорема Пифагора является одной из важнейших теорем в геометрии.
Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
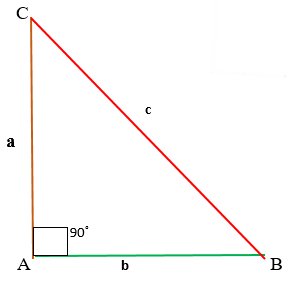
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.
Доказательство теоремы Пифагора
Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).
Теорема доказана.
Следствия из теоремы Пифагора
У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них:
Чему равен квадрат гипотенузы?
Квадрат гипотенузы равен сумме квадратов катетов. со школы наизусть. Это одно из тех правил, которые запомнились навсегда.)))
Еще говорили считалочку «Пифагоровы штаны, во все стороны равны»
Одна из самых известных в геометрии, теорема Пифагора гласит:
Да, квадрат гипотенузы равен сумме квадратов катетов. Вроде так нас учили в школе. Сколько лет прошло, а мы до сих пор помним эту, любимую нами, теорему. Наверное, напрячься и доказать смогу, как по школьной программе.
В соответствие с теоремой Пифагора, квадрат гипотенузы будет равен сумме квадратов катетов.
То есть, AB² = AC² + BC².
Это свойство помогает решать немало геометрических задач.
Существует и несколько другая формулировка этой теоремы: площадь квадрата, который построен на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Геометрия
План урока:
Теорема Пифагора
Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:
Далее возьмем 4 таких треуг-ка и расположим их следующим образом:
Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.
Изучим центральную фигуру, чью площадь мы обозначили как S2. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:
Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:
Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:
Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:
Получили формулу, в которой и заключен смысл теоремы Пифагора:
Изучим несколько простейших примеров использования теоремы Пифагора.
Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.
Решение. Запишем теорему Пифагора:
Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?
Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:
Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.
На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.
Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.
Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.
Решение. В теорему Пифагора вместо букв a и b подставим единицу:
Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.
Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.
Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:
Запишем для одного из них теорему Пифагора:
Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с 2 – это площадь большого (на рисунке – синего)квадрата, а х 2 – площадь маленького:
Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:
Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.
Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:
Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.
Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:
Другой катет находим с помощью теоремы Пифагора:
Задачи на применение теоремы Пифагора
Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.
Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.
Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:
Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.
Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:
Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:
Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.
Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:
Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:
Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.
Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:
Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.
Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:
Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:
Высоту мы нашли. Осталось найти площадь:
Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.
Решение. Найдем длину гипотенузы ВС:
Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:
Аналогично работаем и с ∆АНВ:
Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:
Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?
Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:
Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.
Решение. Опустим на большее основание две высоты:
В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому
∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:
Зная высоту трапеции и ее основания, легко найдем и ее площадь:
Пифагоровы тройки
Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины
Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.
Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение
обращают его в справедливое равенство.
Для удобства такие тройки иногда записывают в скобках.
Например, тройка чисел (3; 4; 5)– пифагорова, так как
Задание. Определите, какие из следующих троек чисел являются пифагоровыми:
Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.
Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.
Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.
Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.
Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:
не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.
Обратная теорема Пифагора
По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:
Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.
Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство
Так как ∆А1В1С1 прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:
а именно это мы и доказываем.
Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:
1) некоторое условие, которое описывает какое-то геометрическое построение;
2) вывод (или заключение), который делается для условия.
В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.
В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.
Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.
Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:
Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.
Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.
Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:
Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда
Формула Герона
Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.
Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:
По рисунку можно записать три уравнения:
Левая часть одинакова в обоих уравнениях, значит, равны и правые:
С учетом этого выразим h 2 :
Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть
Площадь треуг-ка вычисляется по формуле:
Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.
Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?
Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:
Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.
Теорема Пифагора.
Эта теорема – ключик к решению многих задачек с участием прямоугольного треугольника. Её доказал Пифагор в совершенно незапамятные времена, и с тех пор она принесла много пользы знающим её. А самое хорошее в ней то, что она – простая.
Итак, Теорема Пифагора:
Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?
Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.
Правда, похоже на какие – то шорты? Ну и на какие стороны и где она равны? Почему и откуда возникла шутка? А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:
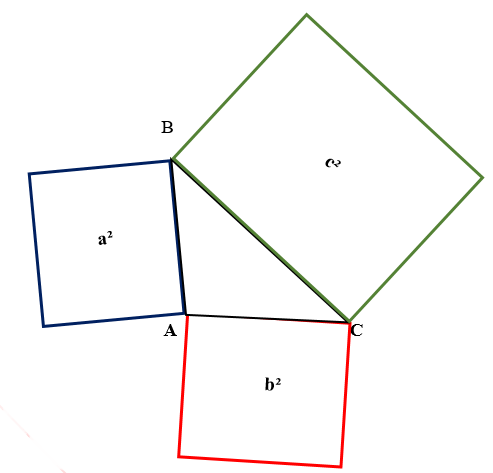
Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.
На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.
Почему же мы сейчас формулируем теорему Пифагора
 |
А Пифагор мучился и рассуждал про площади?
 | или |
Теперь уже должно быть легко:
| Квадрат гипотенузы равен сумме квадратов катетов. |
Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, читай следующие уровни теории, а сейчас пойдём дальше… в тёмный лес… тригонометрии! К ужасным словам синус, косинус, тангенс и котангенс.
Некоторые свойства прямоугольного треугольника:
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Синус, косинус, тангенс, котангенс в прямоугольном треугольнике.
 |
1.
Вообще-то звучит это так:
 | Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. |
 | Значит, |
 | Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. |
А теперь, внимание! Посмотри, что у нас получилось:
Видишь, как здорово:
Это очень удобно – если тебе дан в задаче синус одного угла прямоугольного треугольника, то ты знаешь и косинус другого! Итак, запомни очень твёрдо:
Теперь перейдём к тангенсу и котангенсу.
 | Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. |
Видишь, числитель и знаменатель поменялись местами?
 |
И теперь снова углы и совершили обмен:
| В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого. |
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
История теоремы
Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.
Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.
Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.
Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.
Обратная теорема Пифагора
Обратная теорема Пифагора:
Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.
По теореме Пифагора:
Треугольники ABC и A1B1C1 равны по трём сторонам, поэтому ∠A = ∠A1 = 90°, то есть треугольник ABC является прямоугольным. Теорема доказана.
Нахождение сторон прямоугольного треугольника
Типы прямоугольных треугольников
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
построенных на катетах.
Вычисление расстояния между двумя точками на координатной плоскости
Теорема Пифагора, Формула
Если угол прямой то справедлива формула
Квадрат гипотенузы равен сумме квадратов катетов (это Теорема Пифагора). Теорема Пифагора является частным случаем теоремы косинусов и часто применяется в разнообразных практических и теоретических вопросах.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей, аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим
её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.


что соответствует –
или 
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

треугольника так, как показано на рисунке
Четырёхугольник со сторонами c – квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b). Тогда для константы интегрирования получим:
Примеры задач
Задание 1
В прямоугольном треугольнике один катет равен 3 см, другой – 4 см. Найдите длину его гипотенузы.
Задание 2
Один из катетов прямоугольного треугольника равняется 6 см, а гипотенуза – 10 см. Найдите длину второго катета.
Признаки равенства прямоугольных треугольников
Заключение
Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.
Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).
Чему равен квадрат гипотенузы?
Ответ или решение 2
Теорема Пифагора
Еще в давние времена древнегреческий философ и математик Пифагор определил соотношение между сторонами прямоугольного треугольника.
Так как именно Пифагор доказал эту теорему, ее назвали в его честь.
Теорема гласит, что в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
В алгебре принята другая формулировка:
Квадрат гипотенузы равен сумме квадратов катетов. То есть:
Таким образом, чтобы найти гипотенузу прямоугольного треугольника необходимо:
Ответ: квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора).
Пример решения задачи
Катеты прямоугольного треугольника соответственно равны 12 и 9 см. Найди чему равна гипотенуза треугольника.
Воспользуемся теоремой Пифагора.
1) Найдем сумму квадратов катетов:
12^2 + 9^2 = 144 + 81 = 225.
2) Извлечь квадратный корень из значения суммы:
Ответ: гипотенуза треугольника равна 15 см.
Чему равен квадрат гипотенузы
Основные метрические сооьтношения в прямоугольном треугольнике
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».
А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).
Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.
Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.
Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.
Теорема Пифагора
Сумма квадратов катетов составляет квадрат гипотенузы:
Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.
Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).
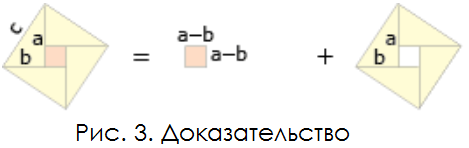
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:
В тригонометрии
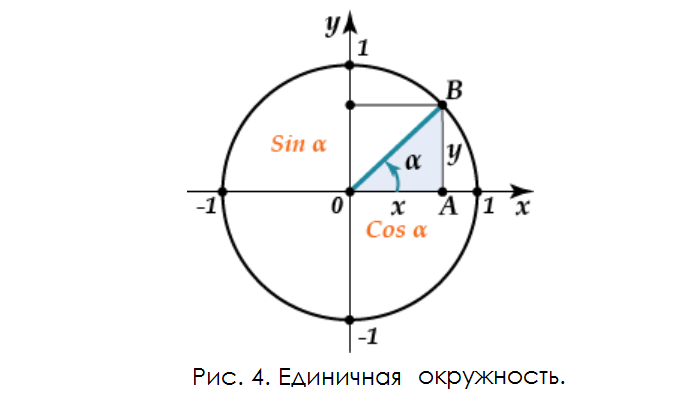
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).
На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.
В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:
sin 2 α + cos 2 α = 1
Гипотенуза прямоугольного треугольника
Связана со сторонами следующими соотношениями (см. рис. 1):
a – противолежащий α катет;
Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.
Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.
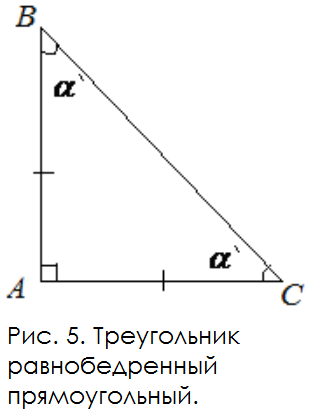
Гипотенуза равнобедренного треугольника
В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.
Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.
Пример решения задачи
Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.
AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:
Ответ: АВ = 21,3 см.
В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.
Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.
Прямоугольные треугольники
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
Подставим найденное значение в формулу косинуса
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Теорема Пифагора: квадрату гипотенузы равна сумма катетов, возведенных в квадрат
Каждый школьник знает, что всегда квадрат гипотенузы равен сумме катетов, каждый из которых возведен в квадрат. Эта утверждение носит название теоремы Пифагора. Она является одной из самых известных теорем тригонометрии и математики в целом. Рассмотрим ее подробнее.
Понятие о прямоугольном треугольнике
Перед тем, как переходить к рассмотрению теоремы Пифагора, в которой квадрат гипотенузы равен сумме катетов, которые возведены в квадрат, следует рассмотреть понятие и свойства прямоугольного треугольника, для которого справедлива теорема.
Сторону, которая лежит против прямого угла, принято называть гипотенузой. Две же другие стороны являются катетами треугольника, они могут быть равны между собой, а могут и отличаться. Из тригонометрии известно, что чем больше угол, против которого лежит сторона в треугольнике, тем больше длина этой стороны. Это означает, что в прямоугольном треугольнике гипотенуза (лежит против угла 90 o ) будет всегда больше любого из катетов (лежат против углов o ).
Математическая запись теоремы Пифагора
Историческая справка
Теорема Пифагора, гласящая, что квадрату гипотенузы равна сумма катетов, каждый из которых возведен в квадрат, была известна задолго до того, когда на нее обратил внимание знаменитый греческий философ. Многие папирусы Древнего Египта, а также глиняные таблички Вавилонян подтверждают, что эти народы использовали отмеченное свойство сторон прямоугольного треугольника. Например, одна из первых египетских пирамид, пирамида Хефрена, строительство которой относится к XXVI веку до нашей эры (за 2000 лет до жизни Пифагора), была построена, исходя из знания соотношения сторон в прямоугольном треугольнике 3x4x5.
Почему же тогда в настоящее время теорема носит имя грека? Ответ прост: Пифагор является первым, кто математически доказал эту теорему. В сохранившихся вавилонских и египетских письменных источниках говорится лишь об ее использовании, но не приводится никакого математического доказательства.
Считается, что Пифагор доказал рассматриваемую теорему путем использования свойств подобных треугольников, которые он получил, проведя высоту в прямоугольном треугольнике из угла 90 o к гипотенузе.
Пример использования теоремы Пифагора
Рассмотрим простую задачу: необходимо определить длину наклонной лестницы L, если известно, что она имеет высоту H = 3 метра, и расстояние от стены, в которую упирается лестница, до ее подножия равно P = 2,5 метра.