Чему равна диагональ квадрата
Чему равна диагональ квадрата
Как посчитать диагональ квадрата? Формула длины диагонали квадрата
Пример
Возьмем, к примеру, квадрат 6 на 6, то есть со стороной, равной шести сантиметрам.
По первому способу: пусть диагональ будет равна С, а боковая сторона — А.
Тогда получим, что С=√А^2+А^2 или С=√2А^2.
Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.
А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2
Теперь видно, насколько второй способ быстрее, легче и самое главное — эффективнее, особенно в таких легких задачках, ведь на экзамене дорога каждая минута!
Видео
Формула вычисления радиуса вписанной окружности через сторону квадрата
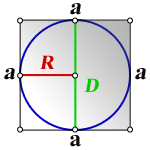
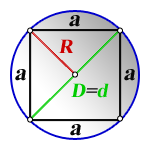
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 | (3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |
Ответ:
Вычисление диагонали квадрата по известной площади
Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.
Используем свойства прямоугольника и запишем формулу его площади.
S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.
Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 | (10) |
Так как AD и BC перпендикулярны, то
  | (11) |
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 | (12) |
Эти реугольники также равнобедренные. Тогда
  | (13) |
Из (13) следует, что
 | (14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Формулы и способы как находить диагональ квадрата
Определения и соглашения
Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Чему равна диагональ квадрата? Как найти диагональ квадрата?
автор вопроса выбрал этот ответ лучшим
Диагональ (с) — это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) — это две стороны квадрата.
Два способа решения.
Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой «а», а длину гипотенузы латинской буквой «с», получаем формулу:
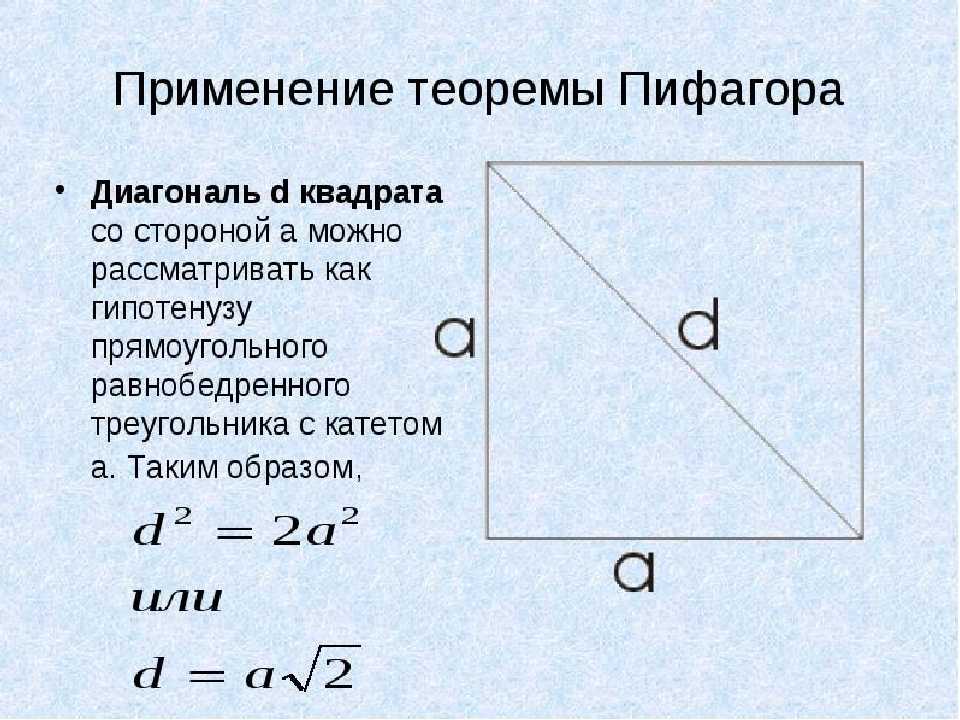
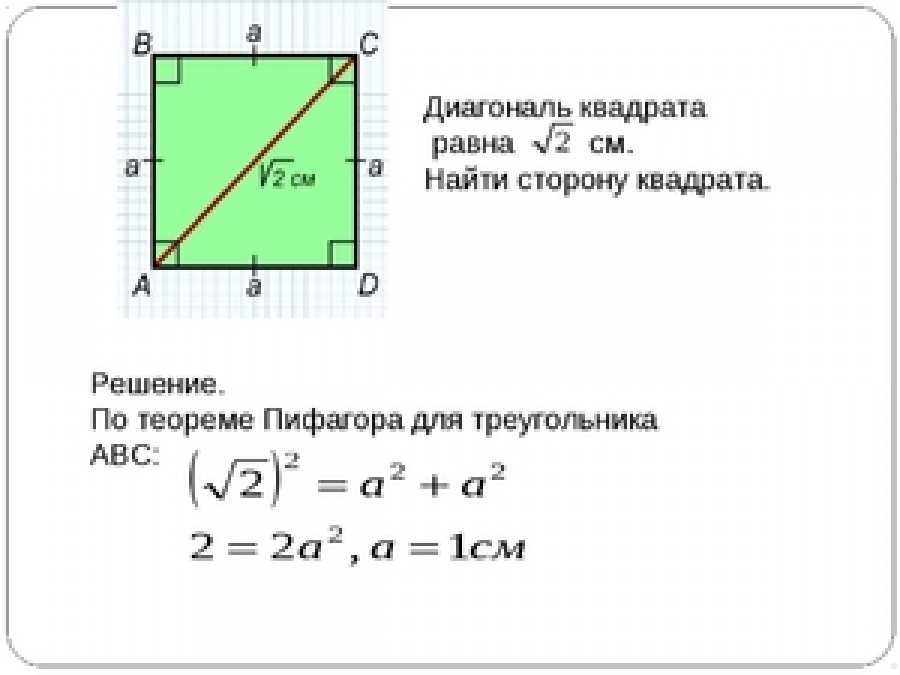
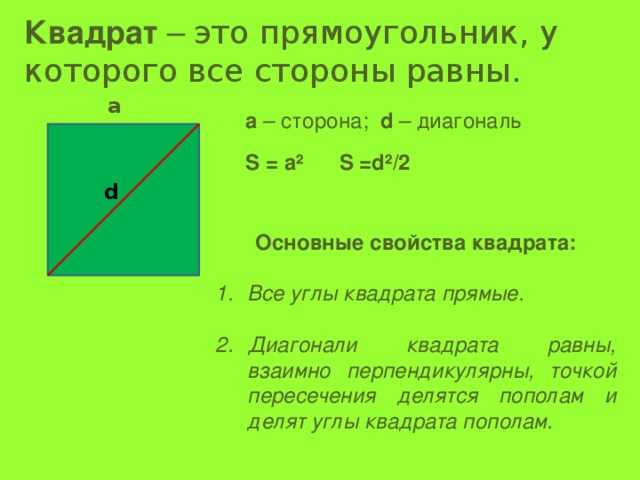

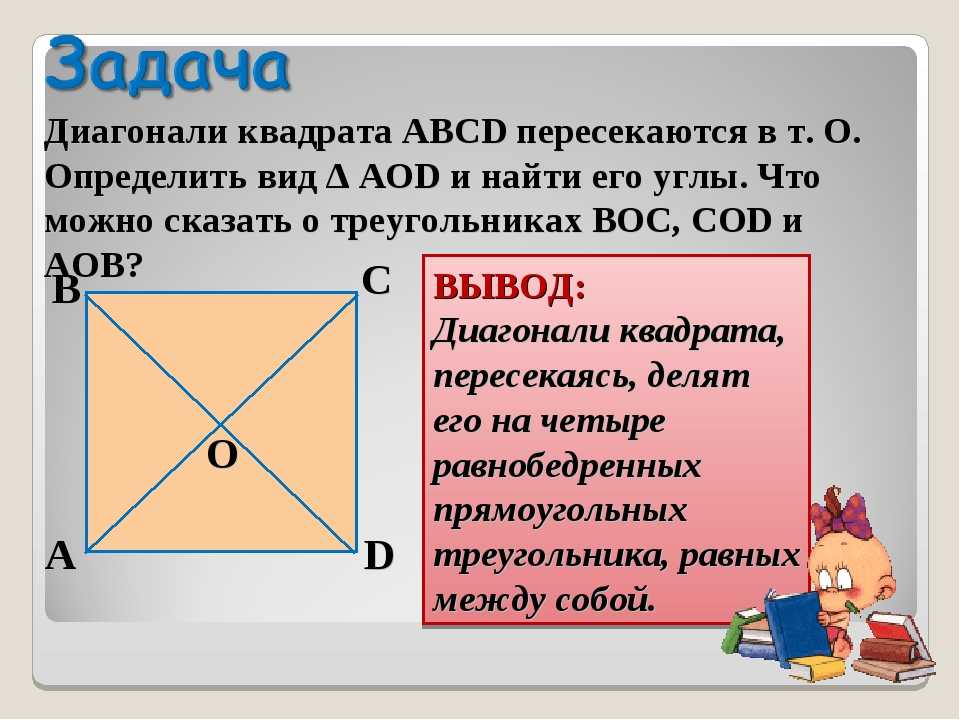
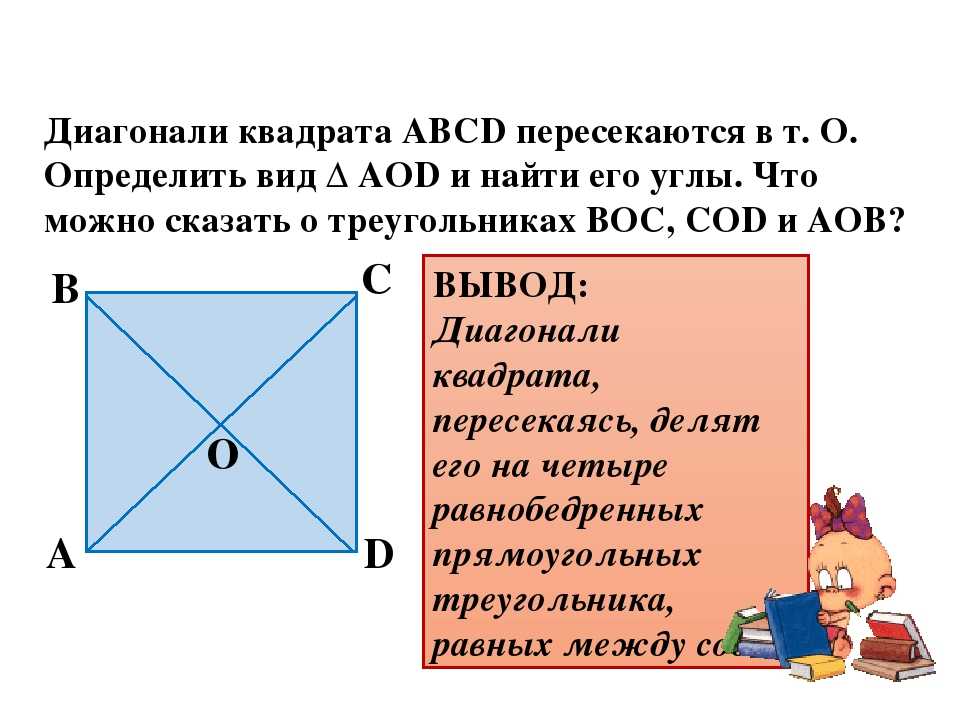
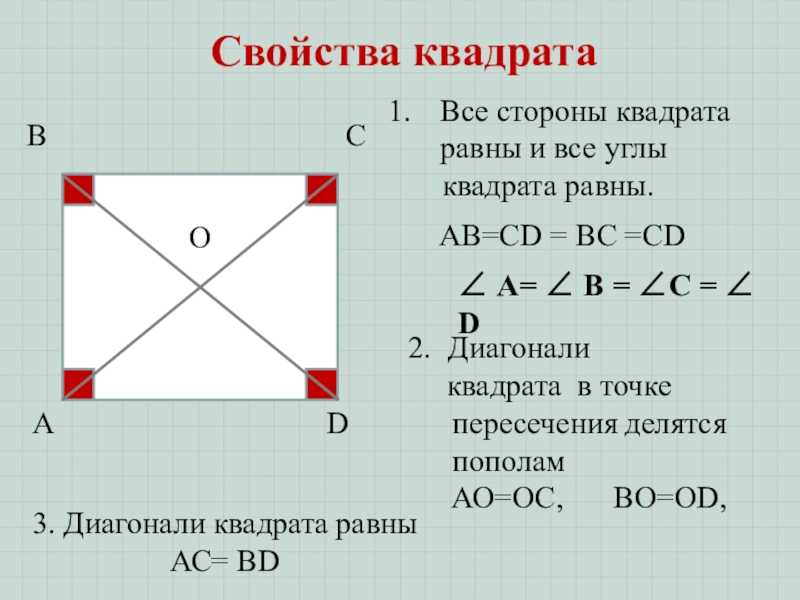
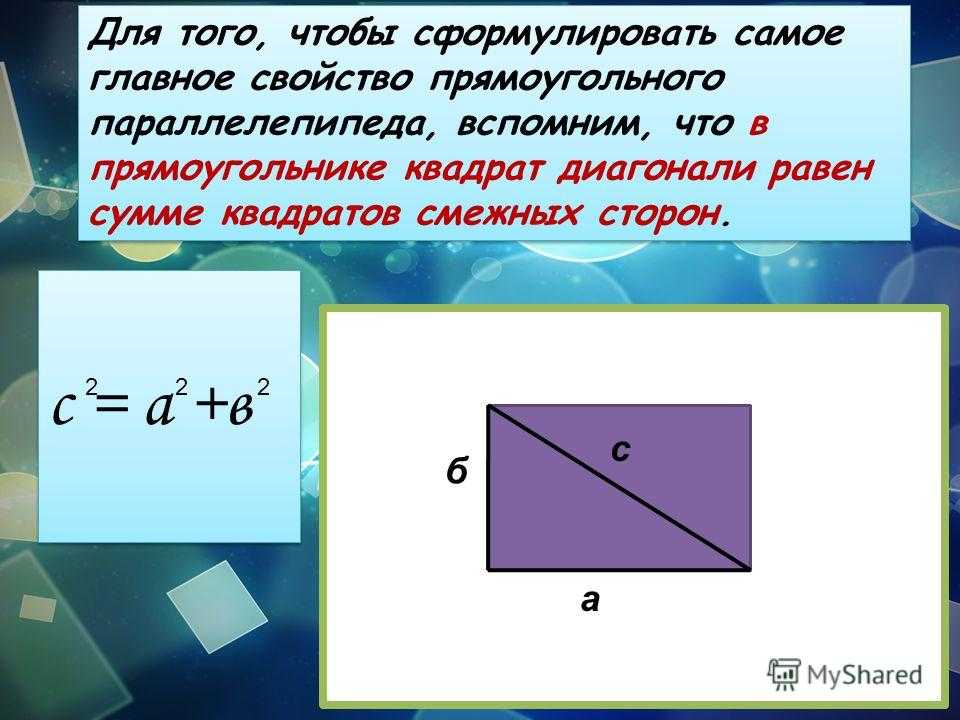
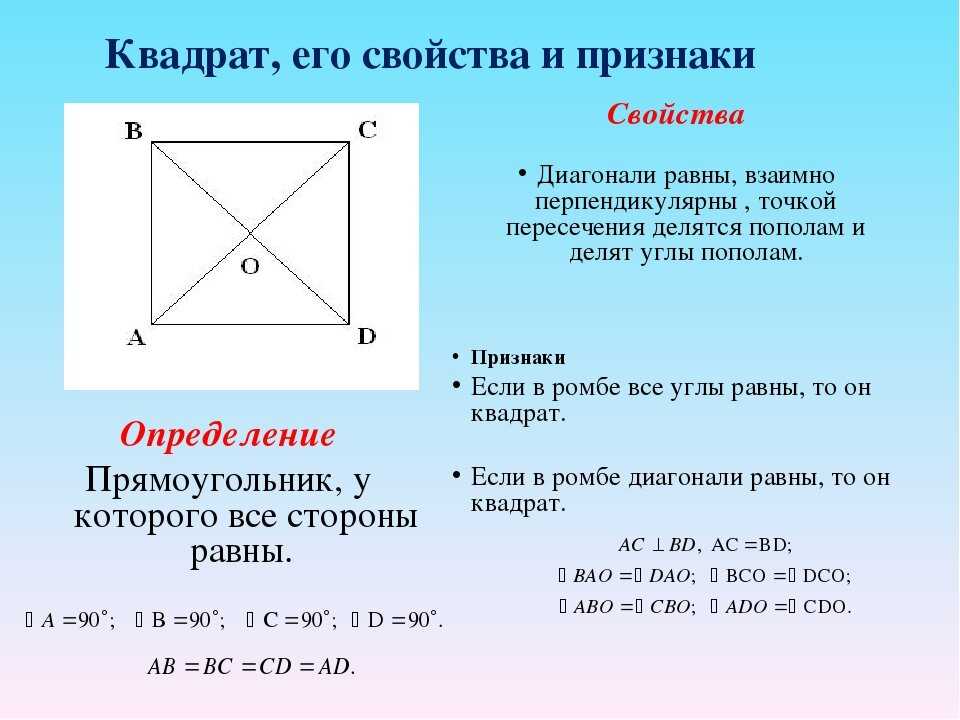
Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.
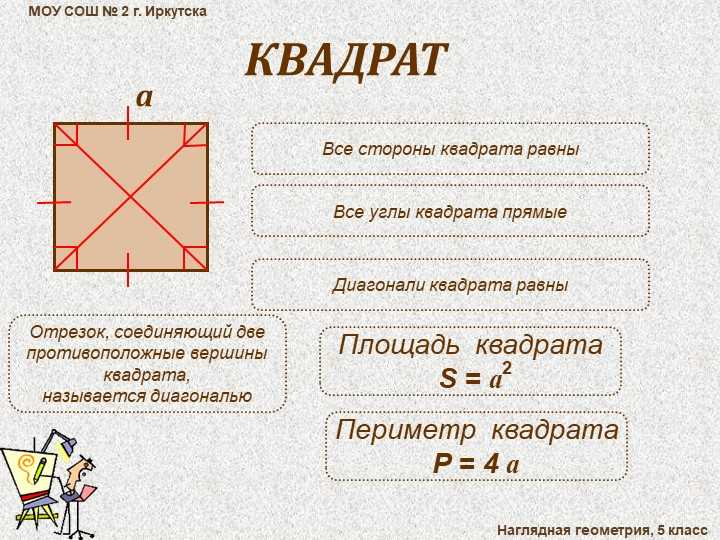
Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины.
В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника.
Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора.
Пусть c — это диагональ, a и b — стороны квадрата, которые по определению равны между собой.
Перепишем формулу в виде:
Выразим диагональ c:
Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.
Диагональ будет равна 10 * √2 см ≈ 14 см.
Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:
К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле
√2*a = √2*100 = 1,4142*100 = 141,42 см.
Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d — длина диагонали, а b — длина одной из сторон.



Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07.
Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.
Так же как и найти гипотенузу у равнобедренного треугольника.
Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны.
Имея в условии слово «квадрат» можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй.
Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.
Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата.
Найти площадь квадрата через диагональ
Главная » Учёба и наука » Математика » Найти площадь квадрата через диагональ
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны. Состоит соответственно из четырёх равных сторон, четырёх вершин и прямых углов 90°.
Как рассчитать площадь квадрата онлайн
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Всё зависит от того, какие данные у вас имеются. Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Смотрите видео по теме:
Геометрические фигуры. Квадрат.
Квадрат — правильный четырёхугольник. У квадрата все углы и стороны одинаковы.
Квадраты различаются лишь длиной стороны, а все 4 угла прямые и равны 90°.
Квадратом может стать параллелограмм, ромб либо прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.
Свойства квадрата.
— у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
— противолежащие стороны квадрата параллельны:
— каждый уг ол квадрата прямой:
— сумма углов квадрата равна 360°:
— каждая диагональ квадрата имеет такую же длину, как и другая:
— каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
— точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
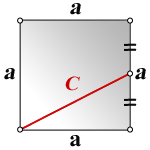
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Что такое квадрат: определение и свойства
В данной публикации мы рассмотрим определение и свойства (с рисунками) одной из основных геометрических фигур – квадрата.
Определение квадрата
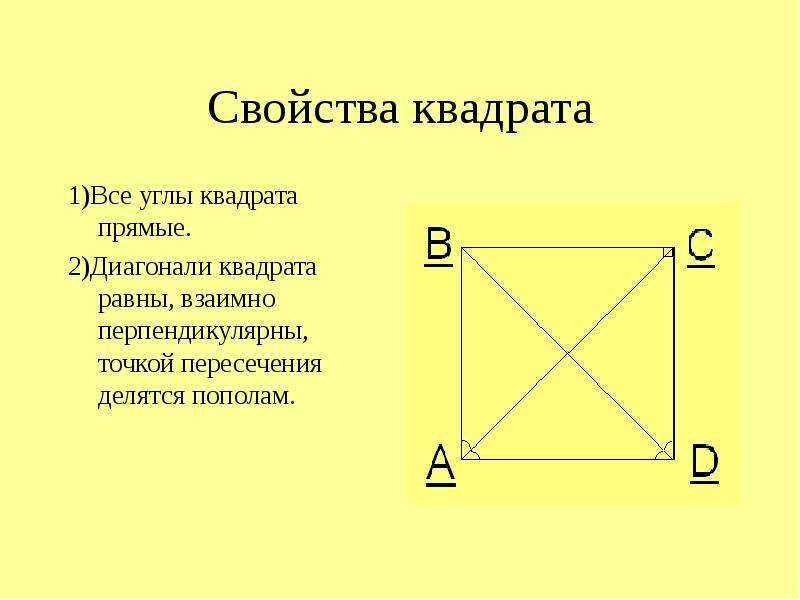
Свойства квадрата
Свойство 1
Диагонали квадрата равны, расположены под прямым углом друг к другу, в точке пересечения делятся пополам.
Свойство 2
Диагонали квадрата являются биссектрисами его углов. Для рисунке выше:
Свойство 3
Центром описанной вокруг и вписанной в квадрат окружностей является точка пересечения его диагоналей (в нашем случае – E).
При этом радиусы окружностей можно вычислить через длину стороны или диагонали квадрата:
Также, один радиус можно выразить через другой:
Свойство 4
Зная длину стороны или диагонали квадрата, можно найти его площадь или периметр.
Периметр (P) квадрата через сторону:
P = a + a + a + a = 4 ⋅ a
Периметр (P) квадрата через диагональ:
Площадь (S) квадрата через сторону:
Площадь (S) квадрата через диагональ:
Свойства диагоналей квадрата, с примерами


В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.
Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.
Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.
Сведения о прямоугольнике
Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.
Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.
Идентификация или признаки
Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем.
Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником.
Для доказательства нужно выполнить такие действия:
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.
Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD.
В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны.
Следовательно, их гипотенузы, которые также являются и диагоналями, равны.
Четвертый признак также доказывается. Следует рассматривать прямоугольный треугольник ABC.
Используя теорему Пифагора, нужно выразить гипотенузу, которая является диагональю фигуры, через катеты (стороны фигуры): AC 2 = AB 2 + BC 2. Таким способом доказывается данный признак.
Последнее утверждение получается из частного случая: если у прямоугольника все стороны равны, то он является квадратом.
Свойства фигуры
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB2 + BC2)^(½). При решении задач применяются свойства прямоугольника:
Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).
Периметр и площадь
Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры.
Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b).
Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:
Площадь — характеристика размерности двумерной фигуры. Ее обозначают литерой S, и измеряют в метрических единицах в квадрате (мм 2, см 2, м 2 и т. д.). Следует отметить, что она вычисляется интегральным методом.
Однако для частных случаев существуют соотношения. Формула, которая является основанием для всех остальных соотношений, называется базовой. Она имеет такой вид: S = a * b.
Площадь находится в зависимости от параметров, которые известны:
Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.
Диагонали и стороны
Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:
Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:
Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.
Другие соотношения
Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:
Пример решения
Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:
Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.
У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20.
Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки.
Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.
Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:
Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.
Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.
Квадрат, его свойства и признаки
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА (I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
– квадрат (по определению), ч.т.д.
ТЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
ТЕОРЕМА (III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
ТЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
ТЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
ТЕОРЕМА (VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
ТЕОРЕМА (VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Найдите периметр квадрата по данным на рисунке.
Урок. «Свойства диагоналей квадрата»
Учитель: Давайте улыбнемся друг другу, пусть улыбки и хорошее настроение будут верными спутниками на сегодняшнем уроке. А наша общая дружная работа поможет разобраться во всем и справиться с любой задачей.
-Все готовы? Значит начинаем!
1. Продолжите ряды чисел.
2. Найдите длину стороны прямоугольника и его периметр.
| ? см | 5 дм | ? м | |||
| 8 см2 | 2 см | 10 дм2 | ? дм | 18 м2 | 2 м |
3. Решите примеры.
Учитель. Ребята, сегодня на уроке мы продолжим работу с прямоугольниками. Поговорим о квадрате. Напомните, что это за фигура – квадрат?
Дети. Квадрат – это прямоугольник, у которого все стороны равны.
Учитель. Верно. А теперь вспомните, что вы знаете о диагоналях прямоугольника?
Дети. Диагонали прямоугольника равны. Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.
Учитель. Верно. А что мы можем сказать о свойствах диагоналей квадрата?
Дети. Так как квадрат – это тоже прямоугольник, значит, его диагонали обладают теми же свойствами.
Учитель. Ребята, как вы думаете, что мы сегодня будем изучать?
Дети. Свойство диагоналей квадрата.
Учитель. Правильно, диагонали квадрата обладают одним интересным свойством: при пересечении диагоналей квадрата всегда получаются прямые углы. Давайте это проверим на чертеже. На с. 17 учебника вверху дан первый чертеж. Возьмите угольник и с помощью его определите, какие углы образовались при пересечении диагоналей.
Дети. Все углы получились прямые.
Учитель. Давайте проверим это еще раз на втором чертеже.
Дети работают в парах со вторым чертежом.
Учитель. Что у вас получилось? Какой вывод можно сделать?
Дети. Да, по чертежу мы еще раз убедились, что при пересечении диагоналей квадрата всегда получаются прямые углы.
Учитель. Молодцы. Теперь, используя это свойство, выполним задание 81. Просят начертить квадрат, длина диагонали которого 5 см. Как будем строить?
Дети. Надо построить два отрезка длиной 5 см так, чтобы они пересекались под прямым углом и чтобы точкой пересечения они делились пополам. Потом соединить концы этих отрезков, и мы получим квадрат.
Учитель. Верно. Выполните это задание у себя в тетради.
5. Работа над пройденным материалом.
Задачу 82 учащиеся решают с комментированием у доски. Вызванный ученик записывает краткое условие:
Учитель.Сначала узнаем, сколько минут мальчик ехал на велосипеде и был в магазине, а потом полученный результата вычтем из общего времени. Только перед выполнением второго действия 1 ч 10 мин надо перевести в минуты.
Приехали – 70 чел. и еще 50 чел.
2. Решение примеров.
Задание 84 учащиеся решают самостоятельно. После происходит взаимная самопроверка.
6.Итоги урока. Рефлексия.
Учитель. Ребята, что нового узнал на уроке? Что повторяли?
Дети. Мы узнали на уроке новое свойство диагоналей квадрата. Решали задачи и примеры.
8. Домашнее задание. (Упр. 85)
Учитель. Ребята, дома вам необходимо будет решить примеры из упражнения 85.
Квадрат. Определение и свойства
1. Длины сторон квадрата равны.
2. Все углы квадрата прямые.
angle ABC = angle BCD = angle CDA = angle DAB = 90^
3. Противолежащие стороны квадрата параллельны друг другу.
AB parallel CD, BC parallel AD
4. Сумма всех углов квадрата равна 360 градусов.
angle ABC + angle BCD + angle CDA + angle DAB = 360^
5. Величина угла между диагональю и стороной равна 45 градусов.
angle BAC = angle BCA = angle CAD = angle ACD = 45^
Квадрат является ромбом Rightarrow AC — биссектриса угла A, и он равняется 45^
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
Так как квадрат это прямоугольник Rightarrow диагонали равны; так как — ромб Rightarrow диагонали перпендикулярны. А так как — параллелограмм, Rightarrow диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
riangle ABD = riangle CBD = riangle ABC = riangle ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
riangle AOB = riangle BOC = riangle COD = riangle AOD
9. Если сторона квадрата равна a, то, диагональ будет равна a sqrt<2>.
Доказывается по теореме Пифагора. Применим ее к riangle ADC.
Отсюда: AC = sqrt<2>cdot a
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
Квадрат. Формулы и свойства квадрата
Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
 |  |
| Рис.1 | Рис.2 |
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:
2. Противоположные стороны квадрата параллельны:
3. Все четыре угла квадрата прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC┴BD | AO = BO = CO = DO = | d |
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.
Диагональ любого квадрата всегда больше его стороны в√2 раз.
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата: 4. Формула диагонали квадрата через радиус описанной окружности:
5. Формула диагонали квадрата через диаметр описанной окружности:
6. Формула диагонали квадрата через радиус вписанной окружности:
7. Формула диагонали квадрата через диаметр вписанной окружности:
8. Формула диагонали квадрата через длину отрезка l:
Периметром квадрата называется сумма длин всех сторон квадрата. 1. Формула периметра квадрата через сторону квадрата:
2. Формула периметра квадрата через площадь квадрата:
3. Формула периметра квадрата через диагональ квадрата:
4. Формула периметра квадрата через радиус описанной окружности:
5. Формула периметра квадрата через диаметр описанной окружности:
6. Формула периметра квадрата через радиус вписанной окружности:
7. Формула периметра квадрата через диаметр вписанной окружности:
8. Формула периметра квадрата через длину отрезка l:
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
1. Формула площади квадрата через сторону квадрата:
2. Формула площади квадрата через периметр квадрата: 3. Формула площади квадрата через диагональ квадрата: 4. Формула площади квадрата через радиус описанной окружности:
5. Формула площади квадрата через диаметр описанной окружности: 6. Формула площади квадрата через радиус вписанной окружности:
7. Формула площади квадрата через диаметр вписанной окружности:
8. Формула площади квадрата через длину отрезка l:
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.
1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата: 2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата: 3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата: 4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата: 5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности: 6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:
7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности: 8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.
Радиус вписанной окружности равен половине стороны квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
1. Формула радиуса круга вписанного в квадрат через сторону квадрата: 2. Формула радиуса круга вписанного в квадрат через диагональ квадрата: 3. Формула радиуса круга вписанного в квадрат через периметр квадрата: 4. Формула радиуса круга вписанного в квадрат через площадь квадрата: 5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности: 6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности: 7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности: 8. Формула радиуса круга вписанного в квадрат через длину отрезка l:
© 2011-2020 Довжик МихаилКопирование материалов запрещено.
Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Квадрат — СПИШИ У АНТОШКИ
Определения и свойства квадрата
«Квадрату» можно дать несколько определений.

Определение 2. Квадрат — это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат — это ромб, у которого все углы прямые.
Свойство 5. Диагонали квадрата равны и пересекаются под прямым углом.
Периметром квадрата называется сумма длин всех сторон квадрата. Периметр обозначается буквой Р.
Онлайн вычисления периметра квадрата можно посмотреть здесь
Площадь квадрата больше площади любого четырехугольника с таким же периметром. Площадь обозначается буквой S.
В старших классах также используются следующие формулы нахождения площади квадрата. Однако они не требуют заучивания, так как представляют собой математические преобразования основных формул, изученных ранее.

Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз. Радиус окружности обозначается буквой R.
Радиус вписанной окружности равен половине стороны квадрата. Радиус вписанной окружности обозначается буквой r.
Матвокс ⋆ диагонали квадрата ⋆ энциклопедия математики
Skip to content
Диагонали квадрата
Свойство равенства диагоналей квадрата
Диагонали квадрата точкой пересечения делятся пополам.
Свойство пересечения диагоналей квадрата следует из свойств прямоугольника:
Пересечение диагоналей квадрата
Диагонали квадрата пересекаются под прямым углом:
Свойство пересечения диагоналей квадрата под прямым углом следует из свойств ромба.
Пересечение диагоналей квадрата
Точка пересечения диагоналей квадрата – это центр квадрата, а также центр описанной и вписанной окружностей.
Точка пересечения диагоналей квадрата
Диагонали квадрата и являются биссектрисами его углов:
Данное свойство диагоналей квадрата следует из свойств ромба.
Диагонали и биссектрисы углов квадрата
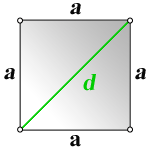
Диагональ квадрата равна произведению его стороны на квадратный корень из двух:
Данное свойство следует из теоремы Пифагора:
Диагональ квадрата через его площадь
Диагональ квадрата через его сторону и площадь
Диагональ квадрата делит его на два равных прямоугольных равнобедренных треугольника, которые являются симметричными фигурами.
Свойство диагонали квадрата
Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника.
Свойства диагоналей квадрата
Диагональ квадрата и описанная окружность
Диагональ квадрата и описанная окружность
Формула диагоналей квадрата
Чему равна диагональ квадрата
Найдите диагональ квадрата, если его площадь равна 364,5.
Пусть сторона квадрата равна Тогда его площадь равна
а диагональ равна
Поэтому диагональ квадрата равна квадратному корню из его удвоенной площади:
Найдите диагональ квадрата, если его площадь равна 0,5.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ квадрата, если его площадь равна 2.
Площадь квадрата равна половине произведения его диагоналей. Поэтому произведение диагоналей равно 4, а каждая из них равна 2.
Пусть сторона квадрата равна Тогда его площадь равна
а диагональ равна
Поэтому:
значит,
Отсюда следует, что диагональ равна 2.
Найдите диагональ квадрата, если его площадь равна 648.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ квадрата, если его площадь равна 2.
Площадь квадрата равна половине произведения его диагоналей. Поэтому произведение диагоналей равно 4, а каждая из них равна 2.
Пусть сторона квадрата равна Тогда его площадь равна
а диагональ равна
Поэтому:
значит,
Отсюда следует, что диагональ равна 2.
Найдите диагональ квадрата, если его площадь равна 512.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ квадрата, если его площадь равна 2.
Площадь квадрата равна половине произведения его диагоналей. Поэтому произведение диагоналей равно 4, а каждая из них равна 2.
Пусть сторона квадрата равна Тогда его площадь равна
а диагональ равна
Поэтому:
значит,
Отсюда следует, что диагональ равна 2.
Чему равна диагональ квадрата
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Это же очень просто подсчитать.
Даже если под рукой нет таблиц квадратных корней или калькулятора.
И даже если вы не помните практически никаких математических формул.
Но теорему-то Пифагора вы помните?
Её все помнят.
Потому что «пифагоровы штаны» врезаются в память.
Это понятно всем, вопросов не вызывает и сразу приходит в голову.
Тормоза возникают при попытке понять, чему равен этот самый квадратный корень из 1800.
(Я понимаю, что математики с хохоту покатываются, но я-то не им объясняю, и сам я тоже не математик, а вовсе даже наоборот).
Хорошо, если со школы осталось в памяти ещё и то, что квадратный корень из произведения равен произведению квадратных корней.
А если не осталось? Если предложение так сделать встречает вопрос: «Почему?»
Значит, всё правильно.
Квадратный корень из произведения равен произведению квадратных корней.
Остаётся заметить, что 18 = 9 х 2.
Квадратный корень из 18 равен 3 умноженным на квадратный корень из 2.
А квадратный корень из 1800 равен 30 умноженным на квадратный корень из 2.
Чему равен квадратный корень из 2, можно в течение минуты найти в интернете.
Даже если под рукой нет таблиц квадратных корней или калькулятора.
Квадрат

Квадрат – прямоугольник с равными сторонами.
Квадрат – параллелограмм, у которого все стороны равны и все углы равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.
Признаки квадрата
Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:
1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.
Описанная окружность
Около квадрата можно описать окружность. Сторона и радиус
окружности связаны соотношением:
Вписанная окружность
В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:
Площадь квадрата
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Все формулы стороны квадрата
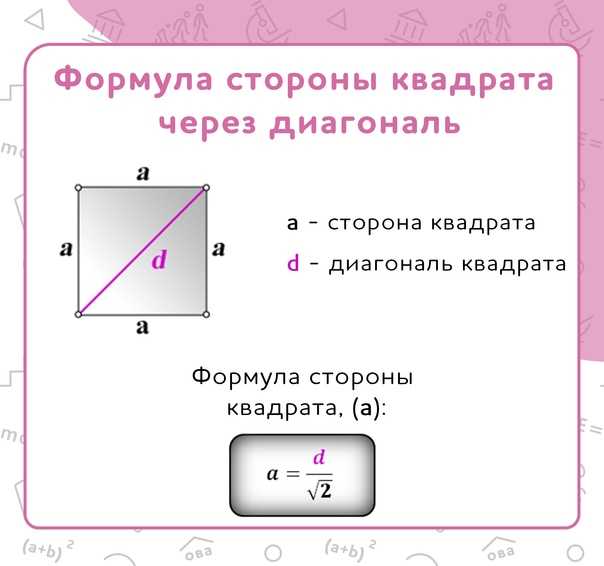
1. Формула стороны квадрата через диагональ
Формула стороны квадрата, ( a ):
2. Формула стороны квадрата через радиус вписанной окружности
Формула стороны квадрата, ( a ):
3. Формула стороны квадрата через радиус описанной окружности
Формула стороны квадрата, ( a ):
4. Формула стороны квадрата через площадь и периметр
Формула стороны квадрата, ( a ):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
Формула стороны квадрата, ( a ):
Чему равна диагональ, если она равна квадрату стороны этого квадрата?
Чему равна диагональ квадрата, если она равна квадрату стороны этого квадрата?
Во-первых, на сколько хватает моих знаний математики, диагональ квадрата- величина линейная: см, метры, км.
равна квадрату стороны
Это уже площадь= метры квадратные, которые никак не могут быть ровны.
Если же вы имели ввиду Стороне квадрата построенного на диагонале (гипотенузе данного квадрата), то тут квадратный корень из суммы квадратов катетов данного квадрата, то есть по теореме Пифагора.
Если рассмотреть треугольник, отсекаемый от квадрата диагональю, можно заметить, что он прямоугольный. Диагональ будет выступать здесь в качестве гипотенузы. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. Пусть сторона имеет значение а, а диагональ значение в. По теореме получаем, что после подстановки данных в в четвертой степени равно удвоенному произведению квадрата а. После сокращения обеих частей равенства на вторую степень числа а, получим, что а в квадрате равняется двум. По условию это и есть гипотенуза.
Квадрат
Квадрат — это четырехугольник, имеющий равные стороны и углы.
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
1. Длины сторон квадрата равны.
2. Все углы квадрата прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^
3. Противолежащие стороны квадрата параллельны друг другу.
AB \parallel CD, BC \parallel AD
4. Сумма всех углов квадрата равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^
5. Величина угла между диагональю и стороной равна 45 градусов.
\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^
Так как квадрат это прямоугольник \Rightarrow диагонали равны; так как — ромб \Rightarrow диагонали перпендикулярны. А так как — параллелограмм, \Rightarrow диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD
9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt <2>.
Отсюда: AC = \sqrt<2>\cdot a
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
Что такое квадрат
Выясним, что такое квадрат и какими свойствами он обладает.
Квадрат — это прямоугольник, у которого все стороны равны.
Так как прямоугольник является параллелограммом, то и квадрат является параллелограммом. А так как все его стороны равны, то он также является ромбом. Отсюда следует, что для квадрата выполняются и свойства прямоугольника, и свойства ромба.
1) Все углы квадрата — прямые.
2) Все стороны квадрата равны.
3) Диагонали квадрата равны.
4) Диагонали квадрата в точке пересечения делятся пополам.
5) Диагонали квадрата взаимно перпендикулярны.
6) Диагонали квадрата являются биссектрисами его углов.

С учетом свойства 3, AO=OC= BO=OD.
5) AC и BD перпендикулярны.
6) AC — биссектриса углов BAD и BCD, — BD биссектриса углов ADC и ABC.
Диагональ квадрата. Формула. Как найти диагональ квадрата?
Длину диагонали квадрата можно найти зная длину его стороны или длину его периметра, или его площадь.
1.Если известна сторона квадрата а, диагональ d будет равна:
2.Если известен периметр (сумма четырёх сторон) P, диагональ будет равна:
3.Если известна площадь квадрата S, диагональ будет равна:
Хотя, если мне не изменяет память, лет десять назад, у нас продавался прекрасный чай «Эдмон» фасовавшийся в цилиндрическую, жестяную упаковку.
Вот это, скажу вам я, заядлая чаевница, был чай с большой буквы. Правда и стоил дороже моего любимого «Липтона», но он того и стоил.
Тогда я сама занималась торговлей и могла себе легко позволит этот самый «Эдмон».
С ним мог конкурировать только красный китайский чай, но его я давно уже не вижу.
Высоту можно провести в любой фигуре при условии, что там есть хоть одна сторона (отрезок поямой) и хоть одна вершина, не принадлежащая этой стороне. И в таком случае перпендикуляр, опущенный из вершины на сторону или на её продолжение, будет высотой.
И квадрат, и прямоугольник этим условиям удовлетворяют.
Люди, имеющие данный аспект, могут быть предрасположены к различного рода излишествам (в еде, вещах, развлечениях) и завышенной самооценке, доходящей до желания выдавать себя за важную персону. Имеют склонность к критиканству, особенно по отношению к власть имущим. В позитивном варианте квадратура Солнца и Юпитера даёт щедрость, искренность и великодушие.
| Квадрат | |
|---|---|
 | |
| Тип | Правильный многоугольник |
| Края и вершины | 4 |
| Символ Шлефли | |
| Диаграмма Кокстера |       |
| Группа симметрии | Двугранный (D4), порядок 2 × 4 |
| Внутренний угол (градусы ) | 90° |
| Двойной многоугольник | Я |
| Свойства | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
Содержание
Характеристики
Свойства
Периметр и площадь
В классические времена, вторая степень была описана как площадь квадрата, как в приведенной выше формуле. Это привело к использованию термина квадрат означать возведение во вторую степень.
Площадь также можно рассчитать по диагонали d согласно с
Что касается по окружности р, площадь квадрата равна
Что касается inradius р, площадь квадрата равна
с равенством тогда и только тогда, когда четырехугольник является квадратом.
Другие факты
Координаты и уравнения
В качестве альтернативы уравнение
также может использоваться для описания границы квадрата с центром координаты (а, б), а горизонтальный или вертикальный радиус р.
строительство
Симметрия
В квадрат есть Dih4 симметрия порядок 8. Есть 2 диэдральные подгруппы: Dih2, Ди1, и 3 циклический подгруппы: Z4, Z2, а Z1.
Эти 6 симметрий выражают 8 различных симметрий на квадрате. Джон Конвей маркирует их буквой и групповым порядком. [12]
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для нерегулярных четырехугольники. r8 полная симметрия квадрата, и а1 нет симметрии. d4 симметрия прямоугольник, и p4 симметрия ромб. Эти две формы двойники друг друга и имеют половину порядка симметрии квадрата. d2 симметрия равнобедренная трапеция, и p2 симметрия воздушный змей. g2 определяет геометрию параллелограмм.
Только g4 подгруппа не имеет степеней свободы, но может рассматриваться как квадрат с направленные края.
Квадраты, вписанные в треугольники
Каждые острый треугольник имеет три вписанный квадраты (квадраты внутри, такие, что все четыре вершины квадрата лежат на стороне треугольника, поэтому две из них лежат на одной стороне и, следовательно, одна сторона квадрата совпадает с частью стороны треугольника). В прямоугольный треугольник два квадрата совпадают и имеют вершину в прямом угле треугольника, поэтому прямоугольный треугольник имеет только два отчетливый вписанные квадраты. An тупой треугольник имеет только один вписанный квадрат со стороной, совпадающей с частью самой длинной стороны треугольника.
Доля площади треугольника, заполненная квадратом, не превышает 1/2.
Квадрат круга
Квадрат круга, предложено древний геометры, это задача построения квадрата той же площади, что и заданная круг, используя только конечное число шагов с компас и линейка.
В 1882 году эта задача оказалась невыполнимой из-за Теорема Линдемана – Вейерштрасса, что доказывает, что Пи ( π ) это трансцендентное число а не алгебраическое иррациональное число; то есть это не корень любой многочлен с участием рациональный коэффициенты.
Неевклидова геометрия
В неевклидовой геометрии квадраты обычно представляют собой многоугольники с 4 равными сторонами и равными углами.
В гиперболическая геометрия, квадратов с прямым углом не существует. Скорее, квадраты в гиперболической геометрии имеют углы меньше прямых углов. Большие гиперболические квадраты имеют меньшие углы.
Перекрещенная площадь
А перечеркнутый квадрат это огранка квадрата, самопересекающегося многоугольника, созданного удалением двух противоположных краев квадрата и повторным соединением его двумя диагоналями. Он имеет половину симметрии квадрата, Dih2, порядок 4. Имеет то же расположение вершин как квадрат, и вершинно-транзитивный. Это выглядит как два 45-45-90 треугольник с общей вершиной, но геометрическое пересечение вершиной не считается.
Перекрещенный квадрат иногда сравнивают с галстук-бабочка или бабочка. то скрещенный прямоугольник связано как фасетирование прямоугольника с обоими частными случаями скрещенные четырехугольники. [13]
Интерьер скрещенного квадрата может иметь плотность полигонов ± 1 в каждом треугольнике, в зависимости от ориентации обмотки по часовой или против часовой стрелки.
Квадрат и скрещенный квадрат обладают следующими общими свойствами:
Графики
K4 полный график часто изображается в виде квадрата со всеми 6 связанными сторонами, поэтому он выглядит как квадрат с двумя нарисованными диагоналями. Этот график также представляет собой орфографическая проекция четырех вершин и 6 ребер правильного 3-симплекс (тетраэдр ).
Геометрические фигуры. Квадрат.
Квадрат — правильный четырёхугольник. У квадрата все углы и стороны одинаковы.
Квадраты различаются лишь длиной стороны, а все 4 угла прямые и равны 90°.
Квадратом может стать параллелограмм, ромб либо прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.
Свойства квадрата.
— у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
— противолежащие стороны квадрата параллельны:
— каждый уг ол квадрата прямой:
— сумма углов квадрата равна 360°:
— каждая диагональ квадрата имеет такую же длину, как и другая:
— каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
— точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Какая диагональ у квадрата 4 × 4?
Нахождение диагонали квадрата
| Квадратный размер | Диагональ |
|---|---|
| 4 « | 5 5 / 8 ″ |
| 4 1 / 2 ″ | 6 3 / 8 ″ |
| 5 « | 7 1 / 8 ″ |
| 5 1 / 2 ″ | 7 3 / 4 ″ |
Отсюда, как найти диагональ? Вы можете найти диагональ прямоугольника, если у вас есть ширина и высота. Чай диагональ равна квадратному корню из квадрата ширины плюс квадрат высоты.
Чему равна диагональ квадрата? Диагональ квадрата рассчитывается по формуле: Диагональ квадрата (г) = √2 × с, Здесь s — сторона квадрата. Диагональная формула вычисляется с помощью теоремы Пифагора. Итак, диагональ квадрата (d) = √2 × s, где s — длина каждой стороны квадрата.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Дополнительно Какова диагональ квадратной тарелки, длина которой 28 см? сторона = 28 см. = 28√2. значит диагональ квадрата 28√2 см.
Сколько диагоналей в квадрате? Квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне. У правильного пятиугольника пять диагоналей одинаковой длины.
Сколько диагоналей в квадрате?
Квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне. У правильного пятиугольника пять диагоналей одинаковой длины.
Чему равна диагональ квадрата 5×5? Как найти диагональ квадрата – формула. Так, например, если сторона квадрата равна 5 дм, то диагональ равна 5√2 дюйма ≈ 7.071 дюйма.
Диагональ квадрата равна стороне квадрата?
Также Что такое квадратная формула? В геометрии квадрат — это фигура с четырьмя равными сторонами. Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s 2 в квадратных единицах.
Чему равна площадь квадрата со стороной 18 см?
Что такое диагональная математика? У прямоугольника две диагонали одинаковой длины. В математике наблюдение за «фактом» часто является причиной постановки новых вопросов. … Более общее определение диагонали многоугольника: отрезок, соединяющий две вершины многоугольника, которые еще не соединены ребром многоугольника.
Как найти длину стороны квадрата, если известна его диагональ?
Какова длина диагонали квадрата со сторонами 7 и корнем 2?
Площадь квадрата = (7^2) квадратных единиц = 49 кв. Единицы. Если длина стороны квадрата равна а, то его диагональ равна а√2. Диагональ =7√2, сторона = диагональ /√2 =7√2/√2 =7 единиц. Площадь = a^2 = 7^2 = 49 квадратных единиц.
Во сколько раз больше диагональ квадрата, чем его сторона? Длина диагонали квадрата равна √2 раза больше его стороны.
Как найти квадрат? Чтобы найти квадрат числа, умножить число само на себя. Например, если вы пытаетесь найти квадрат 5, вы должны умножить 5 на 5 и получить 25, то есть квадрат.
Что такое квадрат 13?
Квадрат 13 является 169.
Как найти длину стороны квадрата, если известна диагональ?
Сколько квадратов в 9 квадрате?
| Размер платы | # Квадраты | # Прямоугольники |
|---|---|---|
| 6 × 6 | 91 | 441 |
| 7 × 7 | 140 | 784 |
| 8 × 8 | 204 | 1,296 |
| 9 × 9 | 285 | 2,025 |
Чему равен периметр числа 625? Площадь квадрата = 625, значит каждая сторона = 625^0.5 = 25 единиц. Периметр квадрата = 100 единиц.
Чему равна площадь квадрата по формуле?
Как найти диагональ фигуры? По формуле, количество диагоналей = n (n-3)/2. Итак, 11-сторонний многоугольник будет содержать 11(11-3)/2 = 44 диагонали. Пример 2. В 20-стороннем многоугольнике одна вершина не образует диагоналей.
Какая диагональ выглядит?
Диагональ сделана из прямая линия, расположенная под углом, а не прямо вверх или поперек. Если вы изобразите квадрат и проведете линию, соединяющую противоположные углы, это будет диагональная линия. Вы найдете диагональные линии в геометрии, а также в мире вокруг вас. … Диагональ может быть существительным или прилагательным.
Что такое диагональ класса 8? Диагональ отрезок, соединяющий две непоследовательные вершины многоугольника.
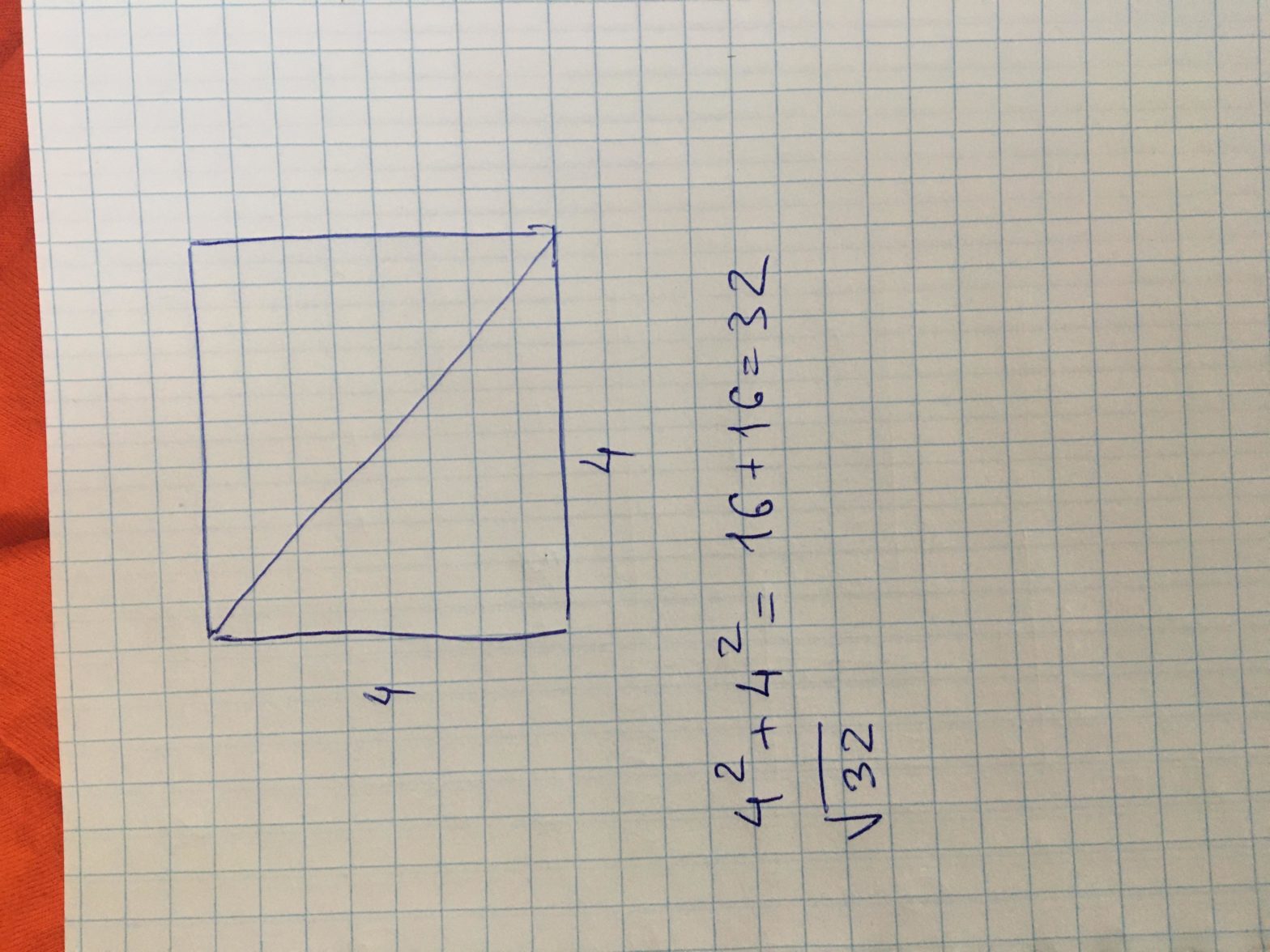



























































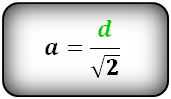
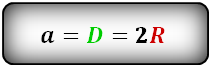
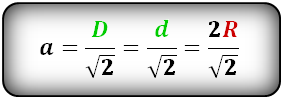
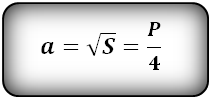

.png)

















