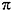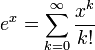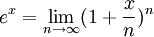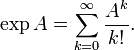Что такое экспонента
Что такое экспонента
Экспонента: определение, формула, свойства, график
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:
График экспоненты
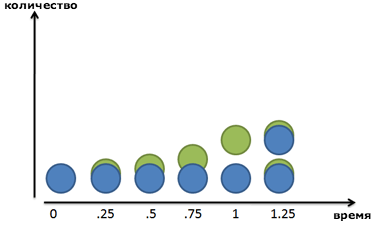
Ниже представлен график экспоненциальной функции
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Что такое Экспонента
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:
Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
И эти вычисления дали нам следующий результат:
Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):
Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Что такое экспонента в математике для чайников
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:
Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
И эти вычисления дали нам следующий результат:
Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):
Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Узнайте также, что такое Число Пи и Логарифм.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Приглядимся поближе
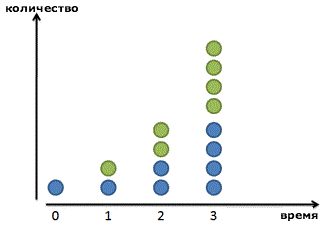
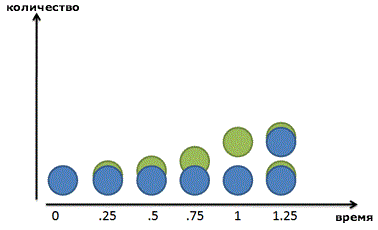
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
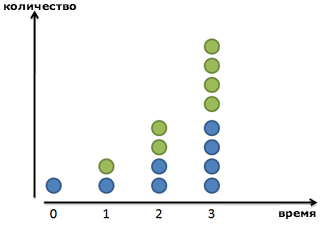
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Экспоненциальная функция
Содержание
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:
или через предел:
Свойства
Экспонента от комплексного аргумента
От комплексного аргумента z = x + iy экспонента определяется следующим образом:
Вариации и обобщения
Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: 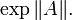
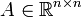
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 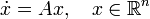
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :
См. также
Полезное
Смотреть что такое «Экспоненциальная функция» в других словарях:
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь
экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика
экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь
экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas
Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь
экспоненциальная — функция [ Словарь иностранных слов русского языка
Что такое экспонента или как заставить чай остывать не так быстро
Константин Катамадзе
Еще у функций есть производная. Это — скорость изменения функции. То есть то, насколько изменится y при небольшом изменении x. Например, в случае функции y=10x производная всегда постоянная: y всегда будет расти в 10 раз быстрее, чем x. А в случае функции y=x 2 производная будет меняться. Если мы увеличим x c 0 до 1, то y тоже увеличится с 0 до 1. А если увеличим x с 1 до 2, то y увеличится с 1 до 4. То есть, производная с ростом x увеличилась.
Бывает, что обратная связь отрицательная: чем больше результат, тем медленнее идет процесс. Например, когда мы голодны, мы начинаем быстро поглощать еду, но как только чувство голода уменьшается, мы начинаем есть спокойно, потом лениво доедаем десерт. Чай остывает тоже по экспоненте: чем больше разность температур между чаем и воздухом, тем быстрее он остывает. Так что, если вам надо срочно отвлечься на 15 минут, а горячего чаю выпить хочется — налейте в него холодного молока или воды. Тогда разница температур уменьшится, и чай не остынет так быстро, как если бы он был горячим.
Экспонента
Скорость изменения этой функции в точности равна ей самой 

Смотреть что такое «Экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Экспонента
Смотреть что такое «Экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Что такое экспонента
Некоторые математические константы были известны издавна: числом Пи пользовались еще в Вавилонском царстве и Древнем Египте, «золотое сечение» же вывел итальянский математик Леонардо Фибоначчи в XIII веке. А число e появилось в 1690 году. Швейцарский математик Якоб Бернулли вычислил его, когда изучал разделы высшей математики — интегральное и дифференциальное исчисление.
Бернулли наткнулся на существование e, решая одну прикладную задачу.
Как мы видим, Бернулли задался вопросом: что если неограниченно увеличивать n в следующей формуле:
В высшей математике это называется «предельным переходом». Учёный определил, что при предельном переходе эта формула дает число: 2,718281828459045…, которое и получило название «число e».
Это число интересно тем, что повсеместно присутствует во многих разделах математики. Встретить его можно в тех областях, где математика «обслуживает» сложные физические процессы — например, затухающие колебания, ядерные реакции, радиоактивный распад и другое.
Затухающее гармоническое движение
Другой пример. Представь себе, что ты биолог и у тебя в специальном стеклянном блюдце (оно называется чашка Петри) с питательным раствором размножаются бактерии. При этом известно, что каждую минуту количество бактерий увеличивается вдвое.
Есть ещё в высшей математике понятие производная от функции. Наглядно — это скорость роста (или убывания) графика функции в каждой точке её графика. Так вот, экспонента замечательна тем, что производная от неё равна самой функции, то есть скорость роста графика экспоненты — это тоже экспонента. И это единственная функция, которая обладает таким свойством.
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
экспонента
Смотреть что такое «экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Экспонента (значения)
 | Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью. |
Полезное
Смотреть что такое «Экспонента (значения)» в других словарях:
Экспонента комплексного переменного — У этого термина существуют и другие значения, см. Экспонента (значения). Экспонента (комплексного переменного) математическая функция, задаваемая соотношением f(z) = ez, где z есть комплексное число. Вообще говоря, такое определение формально и… … Википедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
GHR — (буквенная аббревиатура от фамилий Gennaro, Halevi и Rabin) схема цифровой подписи с открытым ключом. Содержание 1 История … Википедия
Сплайн — (от англ. spline, от [flat] spline гибкое лекало, полоса металла, используемая для черчения кривых линий) функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым… … Википедия
RSA — (аббревиатура от фамилий Rivest, Shamir и Adleman) криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Криптосистема RSA стала первой системой, пригодной и для… … Википедия
IGMP — Название: Internet Group Management Protocol Уровень (по модели OSI): Сетевой Семейство: TCP/IP Назначение протокола: Управление групповой маршрутизацией Спецификация: RFC 3376 IGMP (англ. … Википедия
SNTP — Название: Simple Network Time Protocol Уровень (по модели OSI): Прикладной Семейство: TCP/IP Порт/ID: 123/UDP Назначение протокола: Синхронизация времени Спецификация … Википедия
параметр — 3.4 параметр: Одно из измеряемых свойств испытуемого материала. Источник: ГОСТ Р 52205 2004: Угли каменные. Метод спектрометрического определения генетических и технологических параметров … Словарь-справочник терминов нормативно-технической документации
Привилегированные акции — (Preference shares) Привилегированные акции это акции со специальными правами и ограничениями Привилегированные акции, их особенности, виды, стоимость, дивиденды, конвертация, курс Содержание >>>>>>>>> … Энциклопедия инвестора
Экспонента
Смотреть что такое «Экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
экспонента
Смотреть что такое «экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Функция Exp
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е). е — это число Эйлера,…
В этой статье нет ни слова о коронавирусе!
Экспоненциальный рост – одно из частых выражений в интернете, что же такое экспонента, давайте разложим “по полкам” и на примерах.
В математике экспонента «в чистом виде» — это показательная функция y(x) = ex, производная которой равна самой функции. Коэффициент e = 2,72 (число Эйлера). Рост такой функции происходит очень быстро, чем больше x, тем быстрее рост. К примеру, для х=0 экспонента равна 1, при х=1 функция растет до 2,72, а уже на х=5 она принимает значение 148. На графиках это выглядит как кривая, стремительно поднимающаяся вверх.
Представьте себе снежный ком который катится с горы, он постоянно увеличивается. Чем больше он становится, тем быстрее катится, чем быстрее катится, тем быстрее растет, получается расстояние, которое проходит снежный ком, зависит от времени как экспонента и его скорость выражается той же самой экспонентой.
(При подготовке статьи были использованы материалы кандидата физико-математических наук, старшего научного сотрудника физического факультета МГУ Константина Катамадзе).
Пишите в комментариях о каких новых словах или терминах вы хотели бы узнать.
Мы разложим для вас на канале Всё по полкам. Коротко и ясно
Будьте в курсе и будьте здоровы!
Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Онлайн калькулятор
Просто введите число для которого нужно посчитать экспоненту и получите ответ.
Формальное определение
Показательная функция (синим цветом) и сумма первых
членов ее степенного ряда (красным цветом).
Действительная экспоненциальная функция может быть охарактеризована множеством эквивалентных способов. Обычно это определяется следующим степенным рядом : exp : р → р < Displaystyle ехр двоеточие mathbb
удовлетворяющий начальному условию y ( 0 ) знак равно 1. < displaystyle y (0) = 1.>
Посредством биномиальной теоремы и определения степенного ряда экспоненциальная функция также может быть определена как следующий предел:
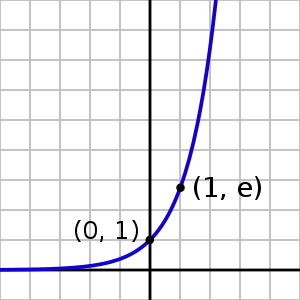
График экспоненты
На графике представлена экспонента, е в степени х.
y ( x ) = е х
На графике видно, что экспонента монотонно возрастает.
Свойства
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
См. также
Как посчитать факториал
Обратная функция
Обратной для экспоненты является натуральный логарифм.
;
.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):
Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Интеграл
См. также раздел “Таблица неопределенных интегралов” >>>
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Узнайте также, что такое Число Пи, Натуральные числа и Логарифм.
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Значение слова «экспонент»
[От лат. exponens, exponentis — выставляющий напоказ]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ЭКСПОНЕ’НТ, а, м. [латин. exponens — выставляющий]. 1. Владелец экспоната, лицо, выставляющее что-н. на выставке (спец.). 2. Показатель степени (мат.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
экспоне́нт I
1. спец. участник выставки, выставляющий, демонстрирующий на ней что-либо ◆ Выставка не удалась, всё лезло врозь, экспоненты остались недовольны, недовольна осталась публика, недовольны газеты. В. Г. Короленко, «Павловские очерки», 1889—1890 г. (цитата из НКРЯ)
3. (в алгебре) показатель степени
4. (в семиотике) объект или знак, представляющий другой объект в иной системе
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: попробованный — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «экспонент»
Предложения со словом «экспонент»
Цитаты из русской классики со словом «экспонент»
Сочетаемость слова «экспонент»
Понятия, связанные со словом «экспонент»
Общество осенних салонов, укороченное название Осенний салон (фр. Société du Salon d’automne, также Salon d’automne) — объединение деятелей искусства во Франции, основанное в 1903 году архитектором Францем Журденом в сотрудничестве с такими художниками, как Жорж Руо, Эдуар Вюйяр, Альбер Марке. В создании общества также принимали участие такие заслуженные мастера живописи, как Сезанн, Ренуар, Одилон Редон, Эжен Каррьер. Ренуар и Каррьер были избраны почётными президентами общества.
Отправить комментарий
Дополнительно
Предложения со словом «экспонент»
Более того, за первые четыре отрезка времени рост экспоненты составляет только малую долю от линейного роста.
Этот показатель называется экспонентом, степенью или порядком числа.
Но внутри шестого отрезка эти линии пересекаются, и ещё через два отрезка значения экспоненты становятся больше уже вдвое, а к десятому – в 10 раз.
Экспонента
Содержание
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
или через предел:
Свойства
Комплексная экспонента
Определим формальное выражение
Сходимость данного ряда легко доказывается:
Свойства
Вариации и обобщения
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: \exp \|A\|. Следовательно, экспонента от матрицы A \in \Bbb
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение \dot x=Ax,
x\in \mathbb R^n с начальным условием x(0)=x_0 имеет своим решением x(t)=\exp (At) x_0.
h-экспонента
Обратная функция
Обратная функция к экспоненциальной функции — натуральный логарифм. Обозначается \ln x :
Экспонента и число е: просто и понятно.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
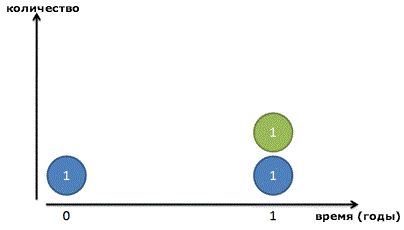
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Но деньги меняют все
С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — свежим денежкам совсем не нужно дозревать, чтобы начать плодоносить.
Основываясь на нашей старой формуле, прирост процента выглядит примерно так:
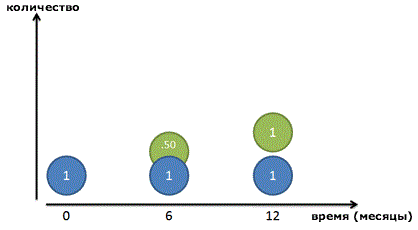
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:
И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:
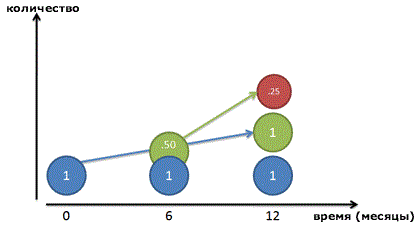
Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:
Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!
Вернемся к формуле. Рост за два полу-периода по 50% составит:
Переходим на составной рост
Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.
Вот так выглядит наш рост, расписанный на 3 составных периода:
Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.
Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:
Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.
Если рассматривать год как 3 равных периода, формула роста будет такой:
рост = (1 + 100%/3) 3 = 2.37037.
Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!
Можно ли преумножать деньги бесконечно?
А почему бы не разбить год на более короткие периоды? Как насчет месяца, дня, часа или даже наносекунды? Наша прибыль взлетит до небес?
Прибыль увеличится, но уже не намного. Попробуем подставить в нашу волшебную формулу разные значения n, и получим следующее:
В математика, экспоненциальная функция это функция формы
куда б положительное действительное число, не равное 1, и аргумент Икс встречается как показатель степени. Для реальных чисел c и d, функция формы ж ( Икс ) = а б c Икс + d < Displaystyle е (х) = ab ^ 
Показательная функция удовлетворяет фундаментальному мультипликативному тождеству (которое может быть расширено до комплексный экспоненты):
Аргумент экспоненциальной функции может быть любым. настоящий или же комплексное число, или даже совершенно другой вид математический объект (например., матрица ).
экспонента
Смотреть что такое «экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
экспонента
Смотреть что такое «экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
ЭКСПОНЕНТ
Полезное
Смотреть что такое «ЭКСПОНЕНТ» в других словарях:
экспонент — Юридическое лицо или индивидуальный предприниматель, демонстрирующий товары и(или) услуги по теме выставки/ярмарки, привлекая для этого собственный или нанятый им персонал. Примечания 1. Под юридическим лицом понимается предприятие или… … Справочник технического переводчика
экспонент — участник, показатель Словарь русских синонимов. экспонент сущ., кол во синонимов: 2 • показатель (22) • … Словарь синонимов
Экспонент — юридическое или физическое лицо участник выставки. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ЭКСПОНЕНТ — ЭКСПОНЕНТ, экспонента, муж. (лат. exponens выставляющий). 1. Владелец экспоната, лицо, выставляющее что нибудь на выставке (спец.). 2. Показатель степени (мат.). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЭКСПОНЕНТ — ЭКСПОНЕНТ, а, м. (спец.). Лицо или организация, экспонирующие кого что н. Экспоненты международной выставки. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ЭКСПОНЕНТ — муж., лат. участник в промышленной или художественной выставке; выставщик. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ЭКСПОНЕНТ — (от лат. exponens выставляющий напоказ) англ. ехhibitor(1); exponent(2); нем. Exponent. 1. Лицо, учреждение, организация, выставляющие к. л. предмет (экспонат) на выставке. 2. В математике показатель степени. Antinazi. Энциклопедия социологии,… … Энциклопедия социологии
ЭКСПОНЕНТ — лицо или организация, выставляющие какой либо предмет на выставке. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М.: ИНФРА М. 479 с.. 1999 … Экономический словарь
экспонент — экспонент. Произношение [экспонэнт] устарело … Словарь трудностей произношения и ударения в современном русском языке
Экспонент — (от нем. exponent Реклама и полиграфия
Число е
Как легко запомнить год рождения Льва Толстого? Вспоминаем первые десять цифр числа е = 2,718281828… Там год его рождения повторяется дважды. 1828 1828. Видимо, специально, чтобы каждый знал, когда родился Великий русский писатель!
Ну а если вы вдруг позабыли, чему равны углы в прямоугольном равнобедренном треугольнике, не проблема. Сразу после дважды Толстого в числе е идет 459045.
Для забывчивых юристов далее спрятался номер статьи из ук Рф «Незаконное осуществление медицинской деятельности или фармацевтической деятельности», в общем, 235 статья.
Сколько градусов в окружности? Смотрим после 235 статьи и видим 360.
Что же такое число е и откуда оно взялось?
Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:
Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.
Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.
Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.
При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.
И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?
Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?
Сам Бернулли определил, что это где-то между 2,5 и 3.

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.
По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.
Экспонента
Для тех, кто не знает, экспонента — это функция:
И она, пожалуй, вызывает куда больший интерес, чем само число е. Хотя бы потому, что производная от этой функции равна самой этой функции.
А если еще вспомнить, что интегрирование — это обратный процесс к дифференцированию, не нужно иметь семь пядей во лбу, чтоб догадаться, что интеграл от e^x так же будет равен e^x.
Но не будем сильно углубляться в математику, а чтобы понять как этим всем пользоваться, ответим на несколько простых вопросов:
Что если мы вкладываем не один рубль, а два?
Число е показывает максимально возможное значение роста единичного вклада при непрерывной капитализации. То есть, если перевести на человеческий язык, с одного рубля при 100% годовых максимум за год набежит е рублей. Если изначальный вклад будет в двое больше, то максимум который мы можем получить через год тоже будет вдвое больше. 2е. Ну или 1000е если положить 1000 рублей.


Что будет через 2-3 года?
Здесь тоже нет ничего сложного, эти 2-3 года уйдут в степень над числом 
Мы говорили, что 






Ну, а если мы имеем дело не со 100%, а скажем 10%?
Проценты в виде постоянной роста (


Почему так происходит? Если не углубляться в математику, то можно сказать, что рост за год при 10% годовых будет такой же, как при 100% годовых за 
Все сказанное можно обобщить и представить в виде формулы:
Причем использовать эту формулу вы можете не только в области финансов. С ее помощью можно спрогнозировать рост населения в нашей необъятной Родине, рассчитать сколько радиоактивного радия останется в Вашем шкафу через год, если предварительно положить туда 10 грамм. Даже можно с легкостью определить когда от этого радия останется ровно половина.
Закон радиоактивного распада
По поводу десяти грамм радия в шкафу я конечно пошутил, но, так или иначе, закон радиоактивного распада можно представить в виде следующего уравнения:
Если решите считать радиоактивные атомы не в штуках, а в привычных килограммах и граммах.
Где 




Хотя чаще всего в учебниках вы можете встретить другое уравнение:
Здесь 
Половина это когда 

В общем можете вооружиться ручкой, бумагой и на досуге из этого:
Ну а если из всего сказанного вы не поняли ровным счетом ничего. И как говорил Виктор Степанович Черномырдин: «Всё это так прямолинейно и перпендикулярно, что мне неприятно». Не расстраивайтесь, по крайней мере, теперь Вы знаете как легко запомнить в каком году родился Лев Николаевич Толстой.
Экспонент
Смотреть что такое «Экспонент» в других словарях:
ЭКСПОНЕНТ — (лат., от exponere выкладывать, выставлять на показ). 1) лицо, поставившее на выставку свои произведения. 2) в алгебре: показатель степени. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭКСПОНЕНТ [лат. exponens… … Словарь иностранных слов русского языка
экспонент — Юридическое лицо или индивидуальный предприниматель, демонстрирующий товары и(или) услуги по теме выставки/ярмарки, привлекая для этого собственный или нанятый им персонал. Примечания 1. Под юридическим лицом понимается предприятие или… … Справочник технического переводчика
экспонент — участник, показатель Словарь русских синонимов. экспонент сущ., кол во синонимов: 2 • показатель (22) • … Словарь синонимов
ЭКСПОНЕНТ — ЭКСПОНЕНТ, экспонента, муж. (лат. exponens выставляющий). 1. Владелец экспоната, лицо, выставляющее что нибудь на выставке (спец.). 2. Показатель степени (мат.). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЭКСПОНЕНТ — ЭКСПОНЕНТ, а, м. (спец.). Лицо или организация, экспонирующие кого что н. Экспоненты международной выставки. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ЭКСПОНЕНТ — муж., лат. участник в промышленной или художественной выставке; выставщик. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ЭКСПОНЕНТ — (от лат. exponens выставляющий напоказ) англ. ехhibitor(1); exponent(2); нем. Exponent. 1. Лицо, учреждение, организация, выставляющие к. л. предмет (экспонат) на выставке. 2. В математике показатель степени. Antinazi. Энциклопедия социологии,… … Энциклопедия социологии
ЭКСПОНЕНТ — лицо или организация, выставляющие какой либо предмет на выставке. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М.: ИНФРА М. 479 с.. 1999 … Экономический словарь
экспонент — экспонент. Произношение [экспонэнт] устарело … Словарь трудностей произношения и ударения в современном русском языке
Экспонент — (от нем. exponent Реклама и полиграфия
Материал из Википедии — свободной энциклопедии
Tell your friends about Wikiwand!
Gmail Facebook Twitter Link
Suggest as cover photo
Would you like to suggest this photo as the cover photo for this article?
Thank you for helping!
Your input will affect cover photo selection, along with input from other users.
Thanks for reporting this video!
This browser is not supported by Wikiwand 🙁
Wikiwand requires a browser with modern capabilities in order to provide you with the best reading experience.
Please download and use one of the following browsers:
An extension you use may be preventing Wikiwand articles from loading properly.
If you’re using HTTPS Everywhere or you’re unable to access any article on Wikiwand, please consider switching to HTTPS (https://www.wikiwand.com).
An extension you use may be preventing Wikiwand articles from loading properly.
If you are using an Ad-Blocker, it might have mistakenly blocked our content. You will need to temporarily disable your Ad-blocker to view this page.
Экспонент
Смотреть что такое «Экспонент» в других словарях:
ЭКСПОНЕНТ — (лат., от exponere выкладывать, выставлять на показ). 1) лицо, поставившее на выставку свои произведения. 2) в алгебре: показатель степени. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭКСПОНЕНТ [лат. exponens… … Словарь иностранных слов русского языка
экспонент — Юридическое лицо или индивидуальный предприниматель, демонстрирующий товары и(или) услуги по теме выставки/ярмарки, привлекая для этого собственный или нанятый им персонал. Примечания 1. Под юридическим лицом понимается предприятие или… … Справочник технического переводчика
экспонент — участник, показатель Словарь русских синонимов. экспонент сущ., кол во синонимов: 2 • показатель (22) • … Словарь синонимов
Экспонент — юридическое или физическое лицо участник выставки. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ЭКСПОНЕНТ — ЭКСПОНЕНТ, экспонента, муж. (лат. exponens выставляющий). 1. Владелец экспоната, лицо, выставляющее что нибудь на выставке (спец.). 2. Показатель степени (мат.). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЭКСПОНЕНТ — ЭКСПОНЕНТ, а, м. (спец.). Лицо или организация, экспонирующие кого что н. Экспоненты международной выставки. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ЭКСПОНЕНТ — муж., лат. участник в промышленной или художественной выставке; выставщик. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ЭКСПОНЕНТ — (от лат. exponens выставляющий напоказ) англ. ехhibitor(1); exponent(2); нем. Exponent. 1. Лицо, учреждение, организация, выставляющие к. л. предмет (экспонат) на выставке. 2. В математике показатель степени. Antinazi. Энциклопедия социологии,… … Энциклопедия социологии
ЭКСПОНЕНТ — лицо или организация, выставляющие какой либо предмет на выставке. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М.: ИНФРА М. 479 с.. 1999 … Экономический словарь
экспонент — экспонент. Произношение [экспонэнт] устарело … Словарь трудностей произношения и ударения в современном русском языке
Экспонент — (от нем. exponent Реклама и полиграфия
Мировые константы «пи» и «e» в основных законах физики и физиологии
Доктор геолого-минералогических наук, кандидат физико-математических наук Б. ГОРОБЕЦ.
(напоминаем, что факториал n! =1 x 2 x 3 x … x n);
(последним дан ряд Ньютона, есть и другие ряды).
Все это так, но, как известно, числа 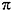
Число 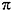
Сначала сформулируем первый основной тезис, а затем поясним его смысл и следствия.
1. Число 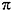
Отсюда вытекают общеизвестные следствия, которые изучают в средней школе.
Разберем еще одну нетривиальную ситуацию, встречающуюся в теории вероятностей. Она касается важной формулы вероятности появления случайной ошибки (или нормального закона распределения вероятностей), в которую входит число 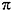
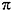
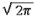
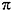
«Замешано» ли число 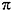
Попробуем разобраться в явлениях, причины которых далеко не ясны, но которые тоже, возможно, не обошлись без числа 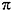
В основе указанных явлений, возможно, лежит так называемый закон распределения максимумов случайных рядов, или «закон троек», сформулированный еще в 1927 году Е. Е. Слуцким.
Число е и однородность времени и пространства
Ясно, что незатухающая волна демонстрирует соблюдение закона сохранения энергии для электромагнитной волны в вакууме. Такая ситуация имеет место при «упругом» взаимодействии волны со средой без потерь ее энергии. Формально это можно выразить так: если перенести начало отсчета по оси времени, энергия волны сохранится, так как у гармонической волны останутся те же амплитуда и частота, то есть энергетические единицы, а изменится лишь ее фаза, часть периода, отстоящая от нового начала отсчета. Но фаза на энергию не влияет именно по причине однородности времени при смещении начала отсчета. Итак, параллельный перенос системы координат (он называется трансляцией) законен в силу однородности времени t. Теперь, наверно, в принципе понятно, почему однородность по времени приводит к закону сохранения энергии.
Далее, представим себе волну не во времени, а в пространстве. Наглядным примером ее может служить стоячая волна (колебания струны, неподвижной в нескольких точках-узлах) или прибрежная песчаная рябь. Математически эта волна вдоль оси О х запишется как e iх =cos х + isin х. Ясно, что и в этом случае трансляция вдоль х не изменит ни косинусоиды, ни синусоиды, если пространство однородно вдоль этой оси. Опять-таки изменится лишь их фаза. Из теоретической физики известно, что однородность пространства приводит к закону сохранения количества движения (импульса), то есть массы, умноженной на скорость. Пусть теперь пространство однородно по времени (и закон сохранения энергии выполняется), но неоднородно по координате. Тогда в различных точках неоднородного пространства оказалась бы неодинаковой и скорость, так как на единицу однородного времени приходились бы различные значения длины отрезков, пробегаемых за секунду частицей с данной массой (или волной с данным импульсом).
Итак, можно сформулировать второй основной тезис:
И все-таки, почему именно число е, а не какое-то другое вошло в формулу Эйлера и оказалось в основании волновой функции? Оставаясь в рамках школьных курсов математики и физики, ответить на этот вопрос непросто. Эту проблему автор обсуждал с теоретиком, доктором физико-математических наук В. Д. Эфросом, и мы попытались пояснить ситуацию следующим образом.
А теперь запишем решение дифференциального уравнения с постоянными коэффициентами, описывающее распространение гармонической волны в среде с учетом неупругого взаимодействия с ней, приводящего к рассеянию энергии или же к приобретению энергии от внешних источников:
f(t) = e (α+ib)t = e αt (cos βt + isin βt).
Сформулированный принцип математически выглядит так: ∆I
Этому закону подчиняются зрение, слух, обоняние, осязание, вкус, эмоции, память (естествен но, пока физиологические процессы не переходят скачком в патологические, когда рецепторы подверглись видоизменению или разрушению). Согласно закону: 1) малому приросту сигнала раздражения в любом его интервале отвечает линейный прирост (с плюсом или минусом) силы ощущения; 2) в области слабых сигналов раздражения прирост силы ощущения гораздо круче, чем в области сильных сигналов. Возьмем для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками. Динамический диапазон биологических рецепторов колоссален: принимаемые глазом сигналы могут различаться по силе в
Следствие 2. Наличие только мнимой части функции при α = 0, β 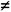
Это следствие возвращает нас к уже рассмотренной выше модели.
Положение о связи законов сохранения с однородностью времени и пространства, бесспорно, правильно для евклидова пространства в классической физике и для псевдоевклидова пространства Минковского в Общей теории относительности (ОТО, где четвертой координатой служит время). Но в рамках ОТО возникает естественный вопрос: а как обстоит дело в областях огромных гравитационных полей, вблизи сингулярностей, в частности, у черных дыр? Мнения физиков здесь расходятся: большинство считают, что указанные фундаментальные положения сохраняются и в этих экстремальных условиях. Однако есть и иные точки зрения авторитетных исследователей. И те и другие работают над созданием новой теории квантовой гравитации.
Фундаментальные константы нашего мира, о природе которых мы говорили, известны не только физикам, но и лирикам. Так, иррациональное число