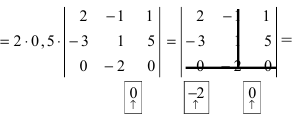
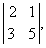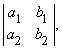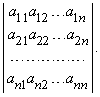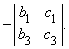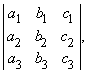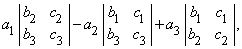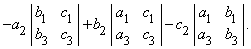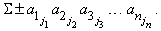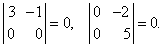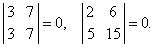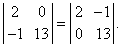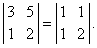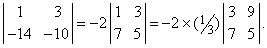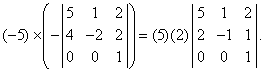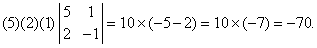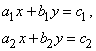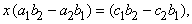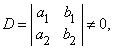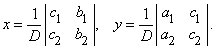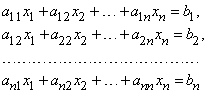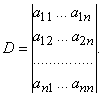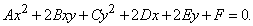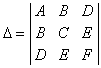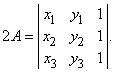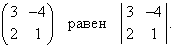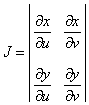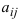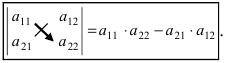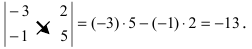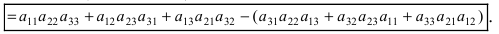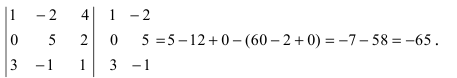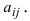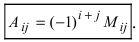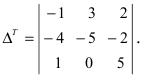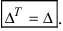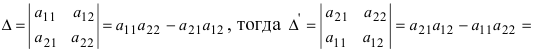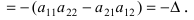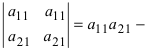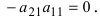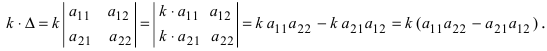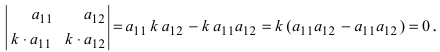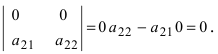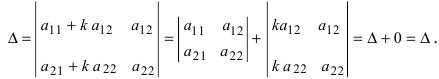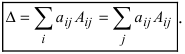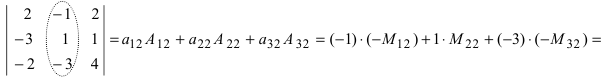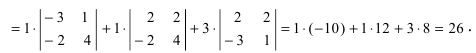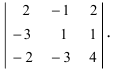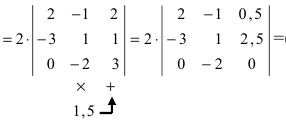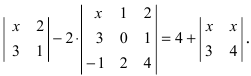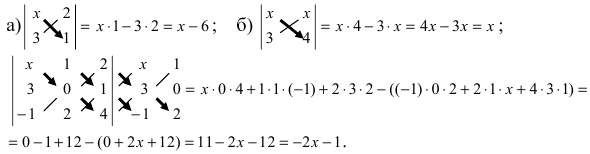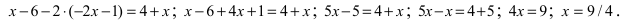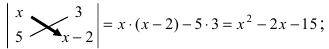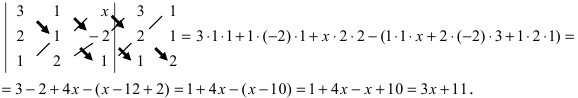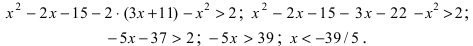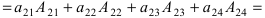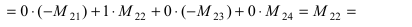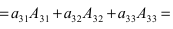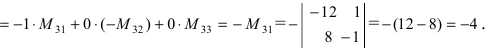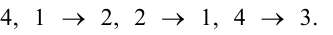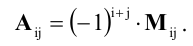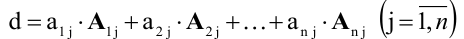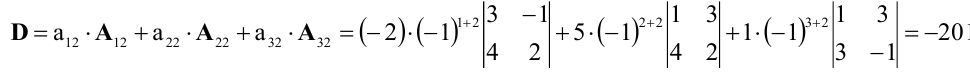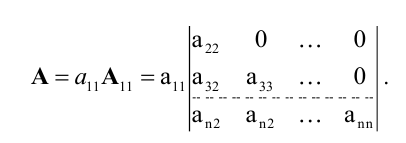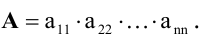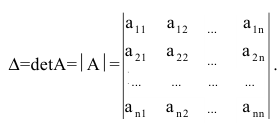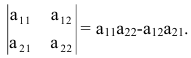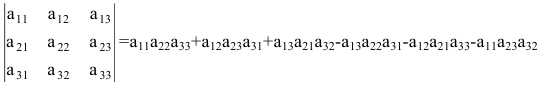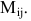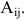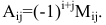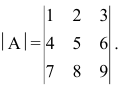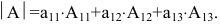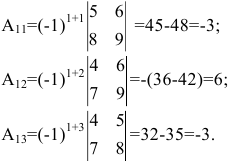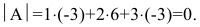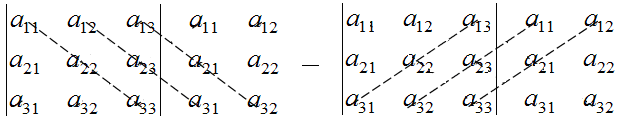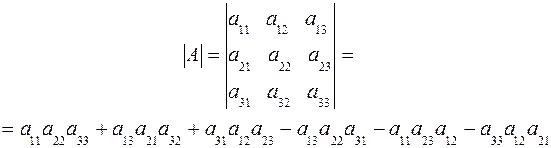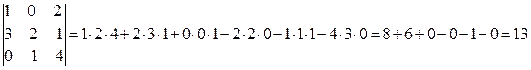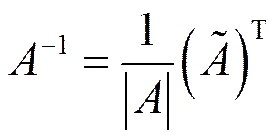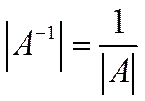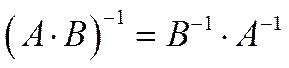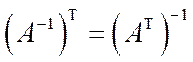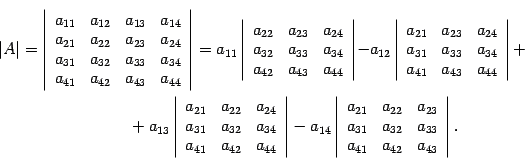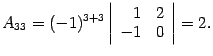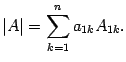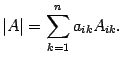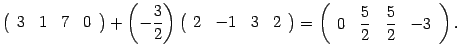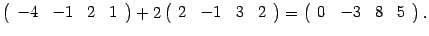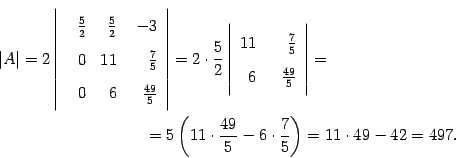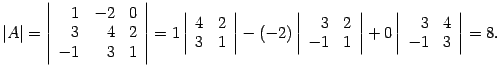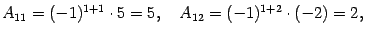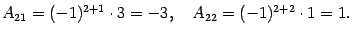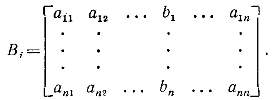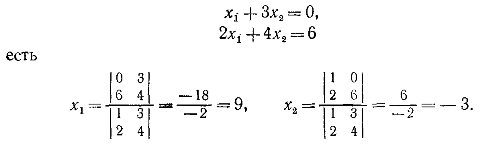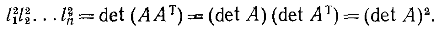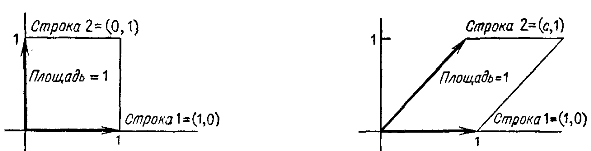Что такое определитель матрицы
Что такое определитель матрицы
ОПРЕДЕЛИТЕЛЬ
ОПРЕДЕЛИТЕЛЬ, или детерминант, – в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число («значение» определителя). Очень часто под понятием «определитель» имеют в виду как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе. Открытие определителей приписывают японскому математику С.Кова (1683) и, независимо, Г.Лейбницу (1693). Современная теория восходит к работам Ж.Бине, О.Коши и К.Якоби в начале 19 в.
Простейший определитель состоит из 4 чисел, называемых элементами и расположенных в виде 2-х строк и 2-х столбцов. О таком определителе говорят, что он 2-го порядка. Например, таков определитель
значение которого равно 2ґ5 – 3ґ1 (т.е. 10 – 3 или 7). В общем случае определитель 2-го порядка принято записывать в виде
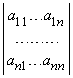
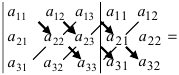
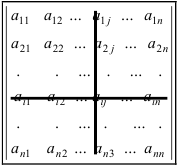
Определитель 3-го порядка состоит из 9 элементов, расположенных в виде 3-х строк и 3-х столбцов. В общем случае определитель n-го порядка состоит из n 2 элементов, и обычно его записывают как
Первый индекс каждого элемента указывает номер строки, второй – номер столбца, на пересечении которых стоит этот элемент, поэтому aij – элемент i-й строки и j-го столбца. Часто такой определитель записывают в виде |aij|.
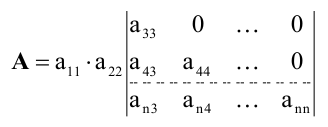
Один из методов вычисления определителя, почти всегда используемый при вычислении определителей высокого порядка, состоит в разложении по «минорам». Минором, соответствующим любому элементу определителя, называется определитель меньшего на 1 порядка, получаемый из исходного вычеркиванием строки и столбца, на пересечении которых стоит этот элемент. Например, минором, соответствующим элементу a2 из определителя
«Алгебраическим дополнением» элемента называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит элемент, четна, и со знаком минус, если она нечетна. В приведенном выше примере элемент a2 состоит в 1-м столбце и во 2-й строке; сумма (1 + 2) нечетна, и поэтому алгебраическое дополнение элемента a2 равно его минору, взятому со знаком минус, т.е.
Значение определителя равно сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения. Например, определитель
разложенный по первому столбцу, имеет вид
а его разложение по второй строке, имеет вид
Вычислив каждый минор и умножив его на коэффициент, нетрудно убедиться в том, что оба выражения совпадают.
Значение определителя.
Под значением определителя
принято понимать сумму всех произведений из n элементов, т.е.
В этой формуле суммирование ведется по всем перестановкам j1, ј, jn чисел 1, 2, ј, n и перед членом ставится знак плюс, если перестановка четна, и минус, если эта перестановка нечетна. Такая сумма насчитывает ровно n! членов, половина которых берется со знаком плюс, половина – со знаком минус. Каждый член суммы содержит по одному члену из каждого столбца и каждой строки определителя. Можно доказать, что эта сумма совпадает с выражением, получаемым при разложении определителя по минорам.
Свойства определителя.
Среди наиболее важных свойств определителя назовем следующие.
(i) Если все элементы любой строки (или любого столбца) равны нулю, то и значение определителя равно нулю:
(ii) Если элементы двух строк (или двух столбцов) равны или пропорциональны, то значение определителя равно нулю:
(iii) Значение определителя не изменится, если все его строки и столбцы поменять местами, т.е. записать первую строку в виде первого столбца, вторую строку – в виде второго столбца и т.д. (такая операция называется транспонированием). Например,
(iv) Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на –2 и прибавляются к элементам первой строки:
(v) Если поменять местами две строки (или два столбца), то определитель изменит знак:
(vi) Если все элементы одной строки (или одного столбца) содержат общий множитель, то этот множитель можно вынести за знак определителя:
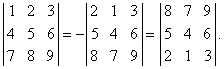
Пример. Вычислим значение следующего определителя 4-го порядка:
Прибавим к 1-й строке 4-ю строку:
Вычтем 1-й столбец из 4-го столбца:
Умножим 3-й столбец на 3 и вычтем из 4-го столбца:
Если угодно, то строки и столбцы можно поменять местами:
Разложим определитель по элементам четвертой строки. Три элемента этой строки равны нулю, ненулевой элемент стоит в третьем столбце, а поскольку сумма (3 + 4) нечетна, его алгебраическое дополнение имеет знак минус. В результате получаем:
Минор можно разложить по элементам третьей строки: два ее элемента равны нулю, а отличный от нуля элемент стоит в третьем столбце; сумма (3 + 3) четна, поэтому предыдущее равенство можно продолжить:
Применения.
Решение системы уравнений
можно получить, если первое уравнение умножить на b2, второе – на b1, а затем вычесть одно уравнение из другого. Проделав эти операции, мы получим
Такая запись решения с помощью определителей допускает обобщение на случай решения системы n линейных уравнений с n неизвестными; каждый определитель будет n-го порядка. Определителем системы линейных уравнений
Заметим, что если D = 0, то уравнения либо несовместны, либо не являются независимыми. Поэтому предварительное вычисление определителя D позволяет проверить, разрешима ли система линейных уравнений.
Определители в аналитической геометрии.
Общее уравнение конического сечения представимо в виде
называется дискриминантом. Если D = 0, то кривая вырождается в пару параллельных или пересекающихся прямых либо в точку (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ).
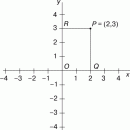
Другой пример: площадь треугольника A с вершинами в точках (обход – против часовой стрелки) (x1, y1), (x2, y2) и (x3, y3) определяется выражением
Связь определителей с матрицами.
Матрицей называется запись массива чисел в виде прямоугольной таблицы. Определители связаны с квадратными матрицами; например, определитель матрицы
Если A, B и С – квадратные матрицы и 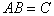
Якобиан.
называется якобианом или определителем Якоби этого преобразования. Если J № 0 в некоторой точке, то в ее окрестности уравнения преобразования можно однозначно разрешить относительно u и v, представив их как функции от x и y.
Содержание:
Определители II и III порядка
Определение: Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу.
Числа
Определение: Определителем II порядка называется число (выражение), записанное в виде квадратной таблицы размером 2×2, т.е. имеющая 2 строки и 2 столбца.
Определение: Определитель II порядка вычисляется по правилу: из произведения элементов, стоящих на главной диагонали, надо вычесть произведение элементов, стоящих на побочной диагонали:
Пример:
Определение: Определителем III порядка называется число (выражение), записанное в виде квадратной таблицы размером 3×3, то есть имеющей 3 строки и 3 столбца.
Определитель III порядка вычисляется по правилу Саррюса: за определителем выписывают первый и второй столбцы, затем из суммы произведений элементов, стоящих на главной диагонали ей параллельных диагоналях, надо вычесть сумму произведений элементов, стоящих на побочной диагонали и ей параллельных:
Пример:
Определение: Минором 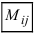
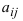
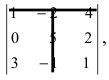
Пример:
Найти миноры элементов 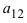
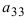
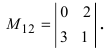
Пример:
Найти миноры элементов 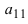
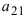
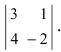
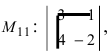
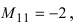
Определение: Алгебраическим дополнением 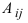
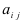
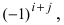
Замечание: Из определения алгебраического дополнения следует, что алгебраическое дополнение совпадает со своим минором, если сумма 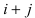
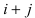
Определение: Транспонированным определителем n-го порядка называется определитель порядка n, полученный из исходного определителя путем замены строк на соответствующие столбцы, а столбцов на соответствующие строки.
Если
Пример:
Найти определитель, транспонированный к определителю 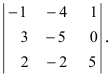
Свойства определителей
1. Величина транспонированного определителя равна величине исходного определителя. Пусть 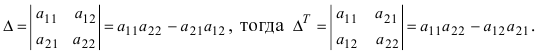
2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. Пусть
Если поменять местами строки (столбцы) четное число раз, то величина и знак определителя не меняется. Нечетная перестановка местами строк (столбцов) не меняет величину определителя, но изменяет его знак на противоположный.
3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. Если определитель содержит два одинаковых столбца, то
4. Для того чтобы умножить определитель на число k, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель k, то его можно вынести за знак определителя.
Докажем это свойство:
5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю.
Пусть в определителе II порядка первая и вторая строки пропорциональны, тогда
6. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.
Пусть в определителе II порядка все элементы первой строки равны нулю, тогда
7. Если элементы какой-либо строки (или столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. Если 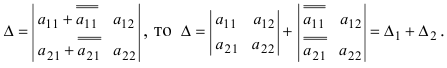
8. Если все элементы какой-либо строки (столбца) умножить на вещественное число к и прибавить k соответствующим элементам другой строки (соответственно, столбца), то величина определителя не изменится.
Умножим элементы второго столбца на вещественное число k и прибавим результат умножения к соответствующим элементам первого столбца, получим
Второй определитель равен нулю по свойству 5.
Замечание: Данное свойство применяется для обнуления всех элементов какой-либо строки (столбца) за исключением одного (метод обнуления), что существенно снижает трудоемкость вычисления определителей порядка выше 3 (см. также свойство 9.).
9. [Метод раскрытия определителя по элементам какой-либо строки (или столбца); универсальный способ вычисления определителя любого порядка]. Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
Пример:
Вычислить определитель 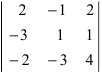
Решение:
Воспользуемся свойством 9.: раскроем определитель по элементам 3 строки 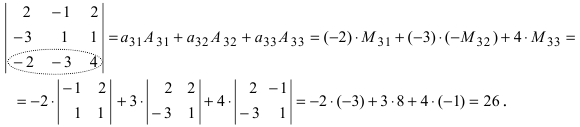
Из полученных результатов видно, что свойство 9. является универсальным методом вычисления любых определителей по элементам любой строки или столбца.
Используя свойство 8. можно обнулить все элементы какой-либо строки (столбца) за исключением одного (метод обнуления), а затем раскрыть определитель по элементам этой строки, воспользовавшись свойством 9.
Пример:
Вычислить определитель
Решение:
Обнулим элементы в третьей строке, для чего выполним следующие действия: 
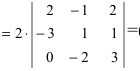
(по свойству 4. из третьего столбца вынесем множитель 0,5, тогда множитель перед определителем станет равным 1)
(раскроем определитель по элементам третьей строки: 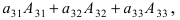
Пример:
Решить уравнение
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное уравнение
Пример:
Решить неравенство
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное неравенство
Пример:
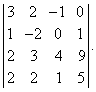
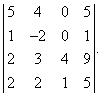
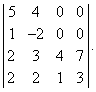
Вычислить определитель четвертого порядка (аналогично выполнить такие же действия с определителем третьего порядка), преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда:
Решение:
Во второй строке исходного определителя присутствуют 1 и 0, поэтому обнуление элементов будем производить в этой строке (при обнулении элементов в строке действия производят со столбцами и наоборот): 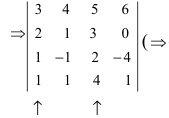
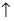
(по методу обнуления раскроем определитель по элементам 2-ой строки ( 
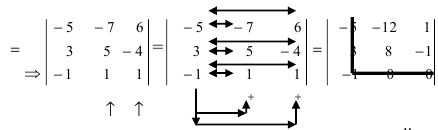
Определители
Перестановкой чисел 1, 2. n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12. n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 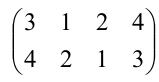
Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 
Пусть нам дана квадратная матрица порядка n
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 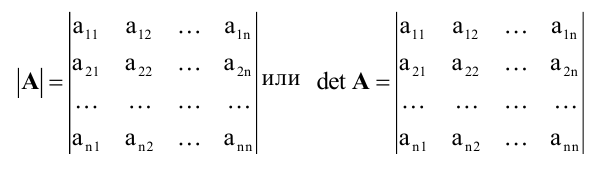
Свойства определителей:
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором 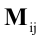
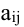
Алгебраическим дополнением элемента 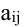
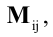
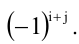
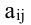
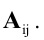
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки 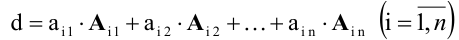
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример:
Не вычисляя определителя 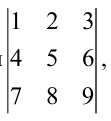
Решение:
Вычтем из второй строки первую, получим определитель 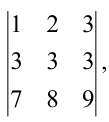
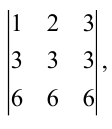
Такой определитель равен нулю.
Пример:
Вычислить определитель 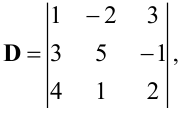
Решение:
Разложим определитель по элементам второго столбца:
Пример:
Вычислить определитель 
Решение:
Разложим определитель А по первой строке:
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
И так далее. После n шагов придем к равенству
Пример:
Вычислить определитель
Решение:
Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
Определители. Алгебраические дополнения
Внимание! Понятие определителя вводится только для квадратной матрицы.
Матрица называется квадратной порядка n, если количество ее строк совпадает с количеством столбцов и равно n.
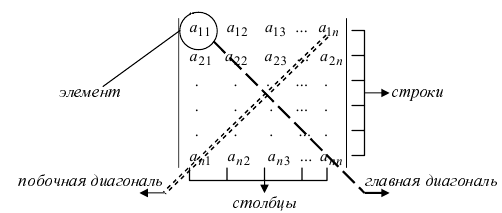
Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ. Элементы квадратной матрицы порядка n, сумма индексов каждого из которых равна n+1, составляют побочную диагональ.
Определитель матрицы 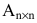
Определитель матрицы второго порядка равен разности элементов главной и побочной диагоналей соответственно:
Определитель матрицы третьего порядка равен сумме элементов главной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали, а также разности элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Схематично это правило изображается так (правило треугольника):
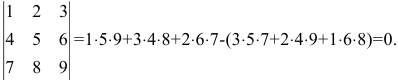
Отметим некоторые свойства определителя.
Минором элемента 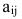
Алгебраическим дополнением элемента 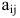
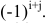
Теорема разложения.
Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения.
Пример №2
Вычислить определитель, разлагая его по элементам первой строки:
Решение:
По теореме разложения
Найдем алгебраические дополнения элементов матрицы А:
Для вычисления определителя порядка выше третьего удобно пользоваться теоремой разложения (метод понижения порядка) или методом приведения определителя к треугольному виду.
Пример №3
Вычислить определитель, приведя его к треугольному виду:
Решение:
Применяя свойство 6 определителей, преобразуем последовательно второй, третий, четвертый столбцы матрицы.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
От действий над матрицами к пониманию их сути…
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
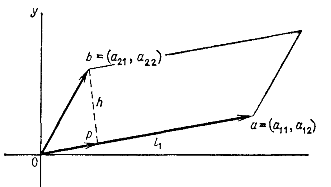
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».
Определители, их вычисление и свойства
Понятие определителя n-го порядка
Пользуясь этой статьёй об определителях, вы обязательно научитесь решать задачи вроде следующей:
Решить уравнение:
и многих других, которые так любят придумывать преподаватели.
Понять логику записи определителей легко по следующей схеме. Возьмём знакомую вам со школьной скамьи систему из двух уравнений с двумя неизвестными:
Например, если дана система уравнений

то из коэффициентов при неизвестных формируется следующий определитель:
Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в n строках (горизонтальных рядах) и в n столбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам, которые мы изучим ниже, находят число, которое и называют определителем n-го порядка и обозначают следующим образом:

Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы
называется главной диагональю, другая диагональ – побочной.
По теме «Определители» на сайте есть также отдельный урок по вычислению минора и алгебраического дополнения.
Вычисление определителей второго и третьего порядков
Покажем, как вычисляются определители первых трёх порядков.
Определитель первого порядка – это сам элемент 

Определитель второго порядка есть число, получаемое следующим образом:

где 
— произведение элементов, стоящих соответственно на главной и на побочной диагоналях.
Пример 1. Вычислить определители второго порядка:
Решение. По формуле (2) находим:
Определитель третьего порядка – это число, получаемое так:

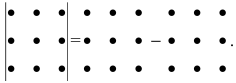
Запомнить эту формулу трудно. Однако существует простое правило, называемое правилом треугольников, которое позволяет легко воспроизвести выражение (3). Обозначая элементы определителя точками, соединим отрезками прямой те из них, которые дают произведения элементов определителя (рис. 1).
На рис.1 главная диагональ и соответствующие ей основания треугольников и побочная диагональ и соответствующие ей основания треугольников выделены красным цветом.
При вычислении определителей очень важно, как и в средней школе, помнить, что число со знаком минус, умноженное на число со знаком минус, в результате даёт число со знаком плюс, а число со знаком плюс, умноженное на число со знаком минус, в результате даёт число со знаком минус.
Пример 2. Вычислить определитель третьего порядка:
Решение. Пользуясь правилом треугольников, получим

Вычисление определителей n-го порядка
Разложение определителя по строке или столбцу
Для вычисления определителя n-го порядка необходимо знать и использовать следующую теорему.
Теорема Лапласа. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.
Определение. Если в определителе n-го порядка выбрать произвольно p строк и p столбцов (p
При разложении определителя часто используется следующее свойство определителя n-го порядка:
если к элементам какой-либо строки или столбца прибавить произведение соответствующих элементов другой строки или столбца на постоянный множитель, то значение определителя не изменится.
Пример 3
здесь разложение проведено по элементам первой строки.
Пример 4.
Предварительно вычтем из первой и третьей строк элементы четвёртой строки, тогда будем иметь
В четвёртом столбце полученного определителя три элемента – нули. Поэтому выгоднее разложить этот определитель по элементам четвёртого столбца, так как три первых произведения будут нулями. Поэтому
Пример 5. Вычислить определитель:
Вычтем из третьей строки элементы первой строки, а к элементам четвёртой строки прибавим элементы первой строки, тогда будем иметь
Приведение определителя к треугольному виду
Определитель, где все элементы, лежащие по одну сторону одной из диагоналей, равны нулю, называется треугольным. Случай побочной диагонали путём изменения порядка строк или столбцов на обратный сводится к случаю главной диагонали. Такой определитель равен произведению элементов главной диагонали.
Для приведения к треугольному виду используется то же самое свойство определителя n-го порядка, которое мы применяли в предыдущем параграфе: если к элементам какой-либо строки или столбца прибавить произведение соответствующих элементов другой строки или столбца на постоянный множитель, то значение определителя не изменится.
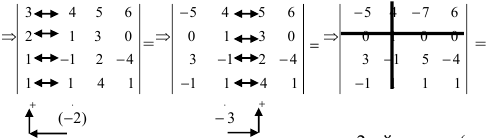
Пример 6. Вычислить определитель:
Произведём следующие преобразования. Вычтем из второй, третьей и четвёртой строк элементы первой строки. Получим определитель треугольного вида:
Этот определитель равен произведению элементов главной диагонали:
Свойства определителя n-го порядка
В двух предыдущих параграфах мы уже использовали одно из свойств определителя n-го порядка. В некоторых случаях для упрощения вычисления определителя можно пользоваться другими важнейшими свойствами определителя. Например, можно привести определитель к сумме двух определителей, из которых один или оба могут быть удобно разложены по какой-либо строке или столбцу. Случаев такого упрощения предостаточно и решать вопрос об использовании того или иного свойства определителя следует индивидуально.
Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е.
Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно.
В самом деле, тогда в каждом члене определителя один из множителей будет нуль.
Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е.
Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю:
Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю:
Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:
Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя, например:
Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:
Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится.
Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится.
Справедливость этого равенства вытекает из свойства 8.
Пример 7. Решить уравнение:
Шаг 1. Вычисляем определитель второго порядка, который находится в левой части уравнения. Элементы главной диагонали перемножаются, из этого произведения вычитается произведение элементов побочной диагонали:
Шаг 2. Вычисляем определитель третьего порядка, который образует правую часть уравнения. Делаем это по «правилу треугольников»:
Приравниваем обе части, получаем уравнение и решаем его:
Понятие определителя матрицы
Свойства определителей:
Все что будет сказано относительно строк, будет относиться и к столбцам.
2 Общий множитель в строке можно выносить за знак определителя.
4 Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
5 Если две строки определителя поменять местами, то определитель поменяет знак.
6 Определитель с двумя равными строками равен нулю.
7 Определитель с двумя пропорциональными строками равен нулю.
8 Определитель, содержащий нулевую строку, равен нулю.
9 Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
10 Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
О том, как правильно понимать определитель матрицы
Расшифровывается это дело следующим образом: если у нас есть матрица
над некоторым полем , то определителем этой матрицы называют сумму всевозможных произведений, состоящих из
элементов этой матрицы, взятых по одному из каждой строки и из каждого столбца, причем каждое произведение входит в эту сумму с тем знаком, который имеет соответствующая перестановка индексов этих элементов в этом произведении.
Другой способ введения определителя связан с его характеристическим свойством. Напомним, полилинейной формой называется функция , определенная на декартовом произведении некоторых векторных пространств
(заданных над одним и тем же полем
), принимающая значения в поле
и линейная по каждому аргументу:
. Форма называется кососимметрической, если при инверсии любых двух (не обязательно соседних) аргументов она меняет знак.
Можно конечно всюду далее рассматривать исключительно поля характеристики 2 и пользоваться «слабым» определением кососимметричности, а можно поступить умнее и немного усилить определение кососимметричности специально для полей характеристики 2 так, чтобы обычная кососимметричность следовала из «сильной». Для этого достаточно потребовать 2 вещи: во-первых, форма должна быть полилинейна, а во-вторых она должна принимать значение ноль всегда, когда среди ее аргументов есть равные. Свойство, которое вытекало из «наивной» кососимметричности для полей характеристики
2 само теперь является составной частью определения кососимметричности (правда только для полей характеристики 2).
Из полилинейности и равенства формы нулю на строках с равными аргументами следует, что если к одному вектору прибавить другой, умноженный на число, то значение формы не изменится. При умножении какого-либо вектора на число 0 сама форма умножается на это число (в частности, если обратить знак какого-либо вектора из набора, то знак самой формы тоже поменяется.
Произвести инверсию векторов в наборе аргументов можно с помощью преобразований этих двух типов. И если внимательно проследить цепочку преобразований, то в конце концов окажется, что форма поменяла знак.
Далее под кососимметричностью будем понимать кососимметричность в «сильном» смысле.
Определение
Определитель матриц— это единственная кососимметрическая полилинейная форма строк матрицы, нормированная единицей на единичном наборе векторов.
Надо сказать, это не самое плохое определение. Но и оно не лишено недостатков. Основные вопросы здесь возникают по поводу кососимметричности. В первую очередь непонятно, почему это свойство вообще важно. Ну меняет функция знак при перестановке двух аргументов и пусть меняет, почему мы так стремимся исследовать именно это свойство, а не какое-нибудь другое. Но здесь все еще хуже. Мы хотим, чтобы форма еще и принимала нулевое значение на наборе, содержащем равные вектора. И в некотором смысле для нас это даже важнее самой кососимметричности, раз мы стали подгонять определение последней под выполнение этого свойства. Все эти экзерсизы с характеристиками выглядят довольно искусственно.
В действительности есть очень простой и естественный пусть построения определителя, при котором все эти вопросы отпадают сами собой. И я постараюсь по возможности максимально последовательно описать этот способ.
Начнем с некоторых предварительных замечаний. Основным объектом изучения линейной алгебры являются конечномерные векторные пространства. Неформально говоря, на любое — мерное векторное пространство над полем
можно смотреть как на «координатное» пространство
, состоящее из упорядоченных наборов длины
элементов поля
. Более строго, пусть у нас есть
— мерное векторное пространство
над полем
. Выбор (упорядоченного) базиса
этого пространства индуцирует изоморфизм
, ставящий в соответствие каждому вектору
набор
его координат в базисе
. Таким образом, во всех дальнейших построениях речь пойдет по большей части про вектора координатного пространства.
Очевидно, некоторый набор векторов пространства
является линейно (не)зависимым, тогда и только тогда, когда соответствующий ему набор векторов пространства
будет линейно (не)зависимым.
Свойство линейной зависимости/независимости действительно очень важно. Дело в том, что система из 1″ alt=»n>1″ src=»https://habrastorage.org/getpro/habr/upload_files/4e1/89f/e1d/4e189fe1dc9b6260122146ddfd0031b7.svg»/>векторов пространства будет линейно зависимой тогда и только тогда, когда найдется вектор в этой системе, который можно линейно выразить через остальные.
Довольно естественным выглядит желание иметь некоторую функцию— индикатор линейной зависимости векторов. Учитывая, что любое векторное пространство «оцифровывается» своим координатным пространством, достаточно иметь такую функцию, определенную на декартовом произведении
копий пространства
и принимающую значения в поле
. Таким образом, мы предъявляем к функции
всего лишь 2 очень естественных требования:
Она должна принимать нулевое значение на любой линейно зависимой системе векторов.
На аргументы этой функции удобно смотреть как на строки матрицы
Заметим, на данном этапе мы еще даже не знаем, существует ли такая функция или нет. Но мы можем в предположении ее существования посмотреть на ее поведение.
. Действительно, строка аргументов, содержащая пару равных значений, очевидно, линейно зависима, а значит функция
будет принимать на ней нулевое значение.
кососимметрична (в любом смысле, учитывая полилинейность + п.1). Доказательство абсолютно аналогично тому, которое находится выше под спойлером.
Рассмотрим, чему равнана некотором наборе строк
:
Здесь мы просто выразили векторы через единичные, затем по полилинейности получили сумму по всем упорядоченным наборам соответствующих произведений, выкинули из них те, которые содержат повторяющиеся аргументы (тем самым получив сумму по всем перестановкам), а затем применили обратные перестановки к единичным векторам.
Смотрим на последнюю строчку в получившейся формуле и видим множитель . Чтобы упростить формулу и не таскать лишний множитель, добавим к тем 2 требованиям к функции
третье требование:
.
Таким образом, если интересующая нас функциясуществует, то она имеет вид:
Нарисовалась знакомая нам формула Лейбница. Самое замечательное то, что в ней нет свободных переменных, а это значит, что мы бесплатно получили единственность интересующей нас функции.
Осталось лишь доказать существование. Капитан намекает, что для этого достаточно взять ту функцию, которая у нас получилась.
А дальше дело техники. Проверяем, что получили мы действительно, что хотели и даже больше. Полученную функцию называем определителем и спокойно приступаем к доказательству основных его свойств.
Определитель матрицы.
Определение. Определителем матрицы n×n является число:
Определитель матрицы A в основном обозначают как de t(A), |A|, либо ?(A).
Свойства определителя матрицы.
Найти определитель матрицы.
Чтобы найти определитель матрицы необходимо знать основные свойства матриц и последовательность действий при решении матрицы.
Для нахождения определителя матрицы, который содержит в матрице функции, используются стандартные методы. К примеру, найти определитель матрицы третьего порядка:
Воспользуемся разложением по первой строке:
Вычислить определитель матрицы.
Вычислить определитель матрицы можно несколькими методами, которые будут перечислены ниже.
В Excel для расчета определителя используется функция =МОПРЕД (диапазон ячеек).
Определитель матрицы и его вычисление
Вы будете перенаправлены на Автор24
В зависимости от порядка матрицы различают несколько способов вычисления определителя.
Определитель матрицы 2-го порядка можно вычислить по формуле:
Для нахождения определителя матрицы 3-го порядка можно использовать одно из двух правил:
Определитель матрицы 3-го порядка с помощью правила треугольника вычисляется по формуле:
Для лучшего запоминания правила треугольника можно пользоваться следующей схемой:
Для вычисления определителя по правилу Саррюса необходимо выполнить следующие действия:
Для лучшего запоминания правила треугольника можно пользоваться следующей схемой:
Готовые работы на аналогичную тему
Для вычисления определителя матрицы 4-го порядка и выше можно использовать один из двух способов:
Разложение определителя матрицы по элементам строки в общем виде можно записать по формуле:
\[\det A=a_
Разложение определителя матрицы по элементам столбца в общем виде можно записать по формуле:
\[\det A=a_ <1j>\cdot A_ <1j>+a_ <2j>\cdot A_ <2j>+. +a_
При разложении определителя по элементам строки (столбца) желательно выбирать строку (столбец), в которой(-ом) есть нули.
Определитель матрицы, содержащей нулевую строку, равен нулю.
Определитель матрицы, содержащей нулевой столбец, равен нулю.
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 18.11.2021
Определители матриц, их свойства и нахождение



Каждой квадратной матрице можно поставить в соответствие некоторое число, вычисляемое по определенному правилу и называемое определителем.
Определитель матрицы А будем обозначать: |А| или D.
Определителем матрицы второго порядка называется число, определяемое по формуле
|А| = 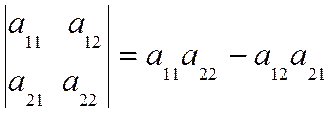
Например, |А| = 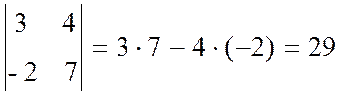
Определителем матрицы третьего порядка называется число, определяемое по формуле
Это число представляет алгебраическую сумму шести произведений, при этом у первых трех произведений знак не меняется, а у последних – меняется на противоположный. Формулу (1.4) можно легко запомнить, используя следующую схему, называемую правилом треугольника или правилом Саррюса:
 |
 |  |
|А| =
Определение определителя матрицы n-го порядка давать не будем, а лишь покажем метод его нахождения.
В дальнейшем, вместо слов определитель матрицы n-го порядка будем говорить просто определитель n-го порядка. Введем новые понятия.
Пусть дана квадратная матрица n-го порядка.
Минором Мij элемента аij матрицы А называется определитель (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.
Алгебраическим дополнением Аij элемента аij матрицы А называется его минор, взятый со знаком (-1) i+j :
т.е. алгебраическое дополнение либо совпадает со своим минором, когда сумма номеров строки и столбца – четное число, либо отличается от него знаком, когда сумма номеров строки и столбца – нечетное число.
Например, для элементов а11 и а12 матрицы А = 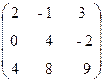
М11 = А11 = 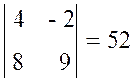
М12 = 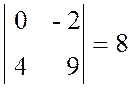
Теорема (о разложении определителя). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения, т.е.
Первая формула называется разложением определителя по элементам i-ой строки, а вторая – разложением определителя по элементам j-го столбца.
Нетрудно понять, что с помощью этих формул любой определитель n-го порядка можно свести к сумме определителей, порядок которых будет на 1 меньше и т.д. пока не дойдем до определителей 3-го или 2-го порядков, вычисление которых уже не представляет трудности.
Для нахождения определителя могут быть применены следующие основные свойства:
1. Если какая-нибудь строка (или столбец) определителя состоит из нулей, то и сам определитель равен нулю.
3. Определитель с двумя одинаковыми или пропорциональными строками (или столбцами) равен нулю.
4. Общий множитель элементов любой строки (или столбца) можно вынести за знак определителя.
5. Величина определителя не изменится, если все строки и столбцы поменять местами.
6. Величина определителя не изменится, если к одной из строк (или к одному из столбцов) прибавить другую строку (столбец), умноженную на любое число.
7. Сумма произведений элементов какой-нибудь строки (или столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю.
8. Определитель произведения двух квадратных матриц равен произведению их определителей.
Введение понятия определителя матрицы позволяет определить еще одно действие с матрицами – нахождение обратной матрицы.
Для каждого ненулевого числа существует обратное число, такое, что произведение этих чисел дает единицу. Для квадратных матриц тоже существует такое понятие.
Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица будет квадратной того же порядка. Однако не каждая квадратная матрица имеет свою обратную.
Матрица А называется невырожденной или неособенной, если ее определитель 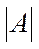
Теорема (о существовании обратной матрицы). Любая неособенная матрица имеет обратную.
Матрицу 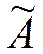
Обратная матрица определяется по формуле
Обратная матрица обладает следующими свойствами:
1.
2.
3.
Из формулы вытекает следующее правило нахождения обратной матрицы.
Для того чтобы для матрицы А найти обратную нужно:
1) найти определитель 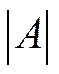
2) найти дополнительную матрицу 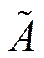
3) транспонировать дополнительную матрицу, т.е. найти 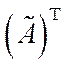
4) разделить каждый элемент транспонированной дополнительной матрицы на значение определителя 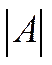
Вычисление определителя
Материал из MachineLearning.
Содержание
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Основные определения и простейшие свойства
Определитель
Определение 1. Определителем квадратной матрицы 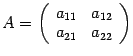
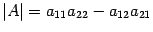
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Утверждение 3. Если в матрице поменять местами две строки, то ее определитель сменит знак.
Утверждение 4. Если матрица имеет две одинаковые строки, то ее определитель равен нулю.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Утверждение 6. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Утверждение 7. Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Утверждение 9. Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Утверждение 10. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Пример. Пусть 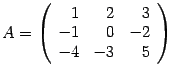
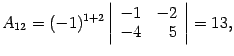
Замечание. Используя алгебраические дополнения, определение 1 определителя можно записать так:
Утверждение 11. Разложение определителя по произвольной строке.
Для определителя матрицы справедлива формула
Пример. Вычислите 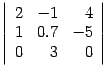
Утверждение 12. Для квадратной матрицы порядка при выполнено соотношение 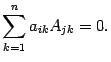
Утверждение 14. Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
Вывод. Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.
Пример. Вычислите определитель матрицы 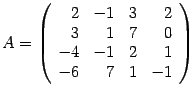
Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :
Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :
Определитель не меняется. В результате получаем
По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число 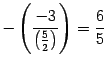
К третьей строке прибавляем первую, умноженную на число 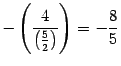
В результате получаем
Обратная матрица
Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица (иначе одно из произведений или было бы не определено).
Если определитель матрицы равен нулю, то обратная к ней не существует.
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Утверждение. Если обратная матрица существует, то она единственна.
Пример. Найдите обратную матрицу для матрицы 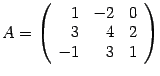
Решение. Находим определитель
Полученная матрица (2) и служит ответом к задаче.
Замечание. В предыдущем примере было бы точнее ответ записать так: 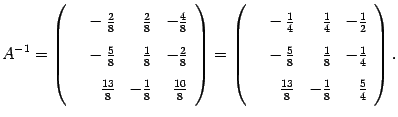
Замечание. При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Пример. Найдите обратную матрицу для матрицы 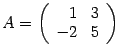
Вывод. Нахождение обратной матрицы по формуле (1) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.
Вычисление определителя и обратной матрицы с помощью метода Гаусса
Метод Гаусса можно использовать для нахождения определителя и обратной матрицы [5, стр.316-317].
Обратная матрица находится решением систем линейных уравнений методом исключения Гаусса:
Формулы для определителя
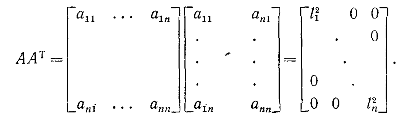
1. Если матрица невырожденная, то и (произведение ведущих элементов).
Знак плюс или минус дается определителем матрицы (или ) и зависит от того, является число перестановок строк в приведении четным или нечетным. Для треугольных сомножителей имеем и
2. Определитель матрицы может быть вычислен разлоразложением по алгебраическим дополнениям i-й строки:
4. Формула для ведущих элементов.
Для разных разложения подматриц «согласованы» друг с другом.
Объем параллелепипеда
Величины суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем
Вектор длины есть разность между вектором второй строки и его проекцией на вектор первой строки.
Площади квадрата и параллелограмма.
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Определитель
Определение
Области использования понятия определителя:
1. (исторически первоначальная) с помощью этой функции устанавливаются условия существования и единственности решения системы линейных уравнений от нескольких переменных; более того, эта функция позволяет компактно записать решение;
2. эта функция позволяет анализировать свойства отображений (функций) одного многомерного множества в другое, см. ☞ ЗДЕСЬ;
3. определитель имеет также ряд геометрических приложений.
Пользуясь только определением, вычислить определитель
Доказательство ☞ ЗДЕСЬ.
Последний результат дает основание для альтернативного определения определителя — симметричного относительно его строк и столбцов.
Определитель матрицы есть сумма всевозможных произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца, и такому произведению приписывается знак согласно теореме.
Элементарные свойства определителя
3. Определитель матрицы равен нулю если она имеет две одинаковые строки (два одинаковых столбца).
Доказательства свойств ☞ ЗДЕСЬ.
Миноры и алгебраические дополнения
Доказательство ☞ ЗДЕСЬ.
Пример. Разложение определителя третьего порядка по первому столбцу:
Для этого в нашем распоряжении имеется такое средство, как преобразования строк или столбцов. В самом деле, на основании общего свойства 6 определителя, к любой его строке можно прибавить любую другую строку, домноженную на произвольное число — определитель от этого не изменится; аналогичное свойство справедливо и для столбцов. Но тогда мы можем упомянутые множители подбирать так, чтобы добиться появления как можно большего количества нулей в отдельной строке (или столбце).
Пример. Вычислить
Систематическое развитие идеи, использованной при решении последнего примера, приводит к основному методу вычисления определителя — методу Гаусса.
Следующий результат имеет исключительно теоретическое значение: используется для доказательства некоторых результатов.
Доказательство ☞ ЗДЕСЬ.
Теорема Лапласа
Имеет место равенство
Пользуясь теоремой Лапласа, вычислить определитель, предварительно преобразовав его:
Биографические заметки о Лапласе ☞ ЗДЕСЬ.
Теорема [Бине, Коши].
Показать, что для квадратных матриц одинакового порядка имеют место равенства
Биографические заметки о Коши ☞ ЗДЕСЬ.
Методы вычисления определителей
Метод приведения к треугольному виду (метод Гаусса)
Пример. Вычислить