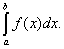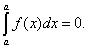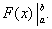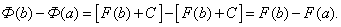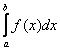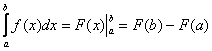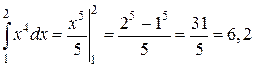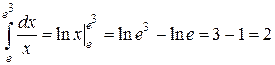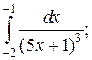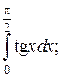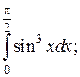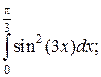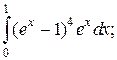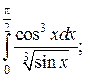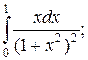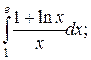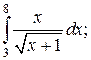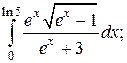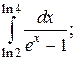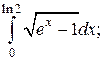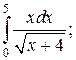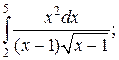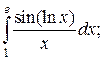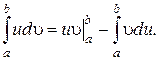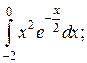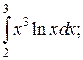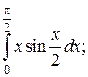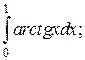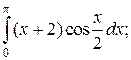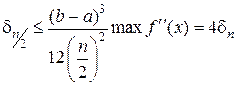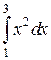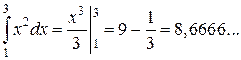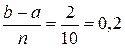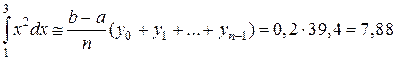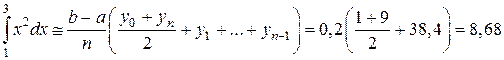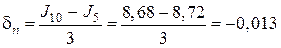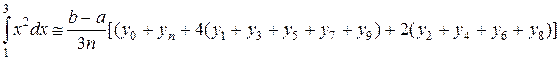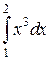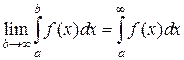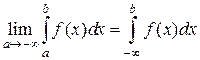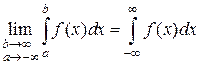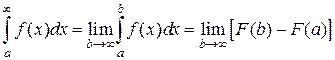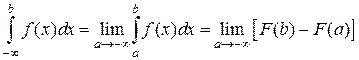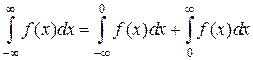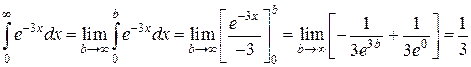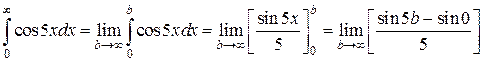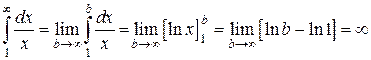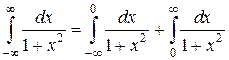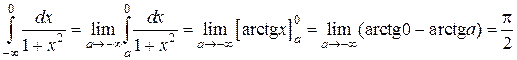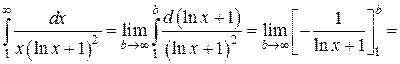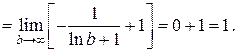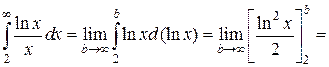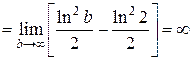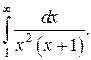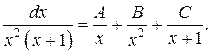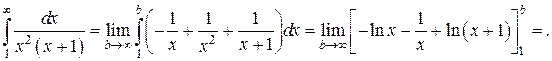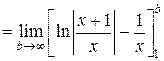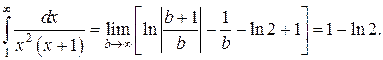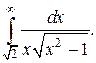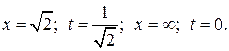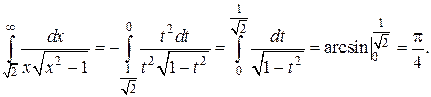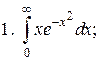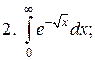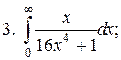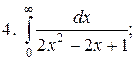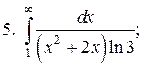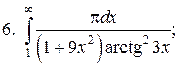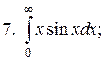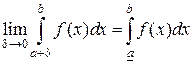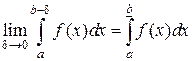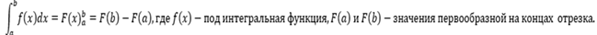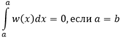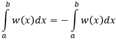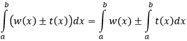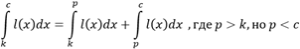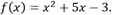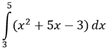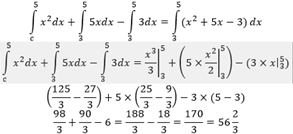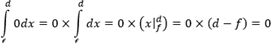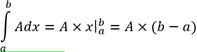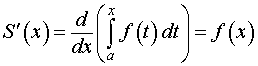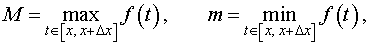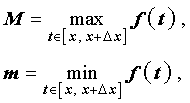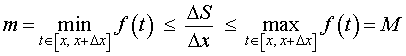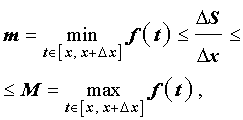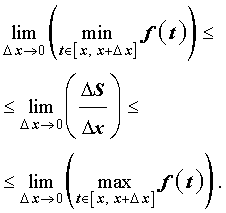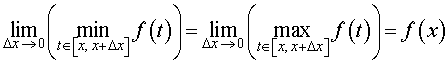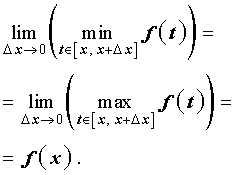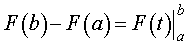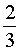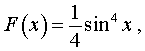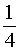Что такое определенный интеграл
Что такое определенный интеграл
Определение и условия существования определенного интеграла
Задачи, приводящие к понятию определенного интеграла.
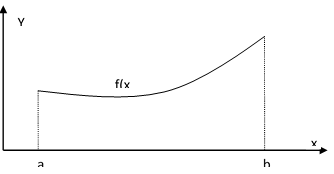
Площадь криволинейной трапеции.
Пусть функция \(f\) непрерывна на отрезке \(\Delta = [a, b]\) и неотрицательна, то есть \(f(x) \geq 0\) при всех \(x \in \Delta\). Рассмотрим фигуру \(G\) (рис. 34.1), ограниченную отрезками прямых \(x = a,\ x = b,\ y = 0\) и графиком функции \(y = f(x)\), то есть
$$
G = \<(x, y): a \leq x \leq b,\ 0 \leq y \leq f(x)\>.\nonumber
$$
Такую фигуру называют криволинейной трапецией, а отрезок \(\Delta\) — ее основанием.
Рис. 34.1
Разобьем отрезок \(\Delta\) на \(n\) частей точками \(x_(i = \overline<1, n-1>)\), где \(x_ <1>Пример 1.
Найти площадь фигуры, ограниченной параболой \(y = x^<2>\) и отрезками прямых \(x = a\), где \(a > 0\), и \(y = 0\) (рис. 34.2).
\(\triangle\) Пользуясь тем, что предел суммы \(\sigma\) для непрерывной функции \(f(x) = x^<2>\) (см. раздел «Классы интегрируемых функций») не зависит от способа дробления отрезка \(\Delta = [0, a]\) и выбора точек \(\xi_\) будем считать, что отрезок \(\Delta\) разбит на \(n\) отрезков равной длины, а в качестве точки \(\xi_\ (i = \overline<1, n>)\) взят правый конец отрезка \(\Delta_\). Тогда \(\xi_ = x_ = \displaystyle \frac
Так как \(\displaystyle \sum_
Заметим, что этот результат был получен еще Архимедом с помощью предельного перехода. Существует также простой способ нахождения предела для \(\sigma\), основанный на формуле Ньютона Лейбница.
Работа переменной силы.
Пусть материальная точка движется вдоль числовой прямой \(Ox\) под действием силы \(P\), причем направление действия силы совпадает с направлением движения материальной точки. Предположим, что сила \(P\) задана как непрерывная функция от координаты \(x\) этой прямой, то есть \(P = P(x)\).
Найдем работу силы \(P\) при перемещении материальной точки от \(x = a\) до \(x = b\). Разобьем отрезок [\(a, b\)], как и в задаче о площади криволинейной трапеции, точками \(x_\) и выберем \(\xi_ \in \Delta_ (i = \overline<1, n>)\). Тогда работа силы \(P\) на отрезке \(\Delta_\) приближенно равна \(P(\xi_)\Delta x_\), а на отрезке [\(a, b\)] работу этой силы можно считать приближенно равной сумме \(\displaystyle \sum_
В рассмотренных задачах речь идет о нахождении предела сумм вида \(\displaystyle \sum_
Понятие определенного интеграла.
Пусть функция одного переменного \(f(x)\) определена на отрезке [\(a, b\)] и пусть \(x_ (i = \overline<0, n>)\) — совокупность точек этого отрезка таких, что
$$
a = x_ <0>Определение.
Если существует число \(J\), определяемое условиями \eqref
Понятие определённого интеграла



Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 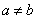
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
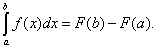
При a = b по определению принимается
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
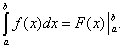
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Из всех первообразных для f(x) выбирается обычно та, которая соответствует равной нулю производной постоянной, и к ней применяется формула Ньютона-Лейбница.
1.1. Понятие определённого интеграла
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Нижний предел интегрирования стандартно обозначается буквой 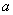
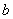
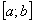
И перед тем, как перейдём к практике, небольшое faq по теме:
Что такое определенный интеграл? С формальной точки зрения, определённый интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число:
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти это число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу перепишите на листок и наклейте на самом видном месте!
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию 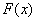
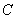
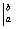
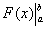
2) Подставляем значение верхнего предела в первообразную функцию: 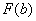
3) Подставляем значение нижнего предела в первообразную функцию: 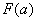
4) Рассчитываем (без ошибок!) разность 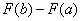
Вопрос следующий, а на самом деле первый: всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 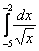
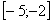
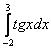
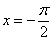
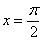
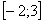
Таким образом, чтобы определенный интеграл вообще существовал, нужно чтобы подынтегральная функция была непрерывной на отрезке интегрирования. Понятие непрерывности тоже интуитивно понятно – если график можно начертить, не отрывая карандаша от бумаги, то данная функция непрерывна на этом участке.
И из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, желательно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.
В противном случае может получиться такой казус: 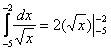
А сделать надо следующее: предварительно проверить функцию на непрерывность. И если для решения (в контрольной работе, на зачете, экзамене) вам предложен несуществующий интеграл вроде 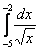
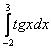
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим посвящена следующая глава.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике:
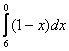
Без чего не обходится математика? Конечно же, без всевозможных свойств:
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Определенный интеграл
В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как площадь, объём, масса, смещение и т. д., когда задана скорость или распределение изменений этой величины по отношению к некоторой другой величине (положение, время и т. д.).
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.
Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию.
Содержание
Типы интегралов
История
Знаки интеграла 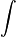
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
См. также
Ссылки
Полезное
Смотреть что такое «Определенный интеграл» в других словарях:
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — (definite integral) Интеграл функции, вычисляемый на интервале, ограниченном верхним и нижним пределами. Если первой производной функции F(х) является f(x), то определенный интеграл f(x) равен F(x)+k. Определенный интеграл f(x) на интервале с… … Экономический словарь
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интегральное исчисление … Большой Энциклопедический словарь
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интеграл … Математическая энциклопедия
ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… … Экономический словарь
ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь
Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия
ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия
интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика
интеграл Джоуля I2t — интеграл Джоуля Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента … Справочник технического переводчика
Интеграл — [integral]. Есть два различных понятия неопределенный И. и определенный И. Говорят, что функция f(x) имеет неопределенный И. ∫f(x)dx, если существует такая функция F(x), что ее производная dF(x)/dx равна исходной функции f(x). Функция F(x)… … Экономико-математический словарь
Определенный интеграл и его свойства
Ранее мы рассматривали определенный интеграл как разность значений первообразной для подынтегральной функции. При этом предполагалось, что подынтегральная функция имеет первообразную на промежутке интегрирования.
В случае, когда первообразная выражается через элементарные функции, мы можем быть уверенными в ее существовании. Но если такого выражения нет, то вопрос о существовании первообразной остается открытым, и мы не знаем, существует ли соответствующий определенный интеграл.
Геометрические соображения подсказывают, что хотя, например, для функции нельзя выразить первообразную через элементарные функции, интеграл существует и равен площади фигуры, ограниченной осью абсцисс, графиком функции и прямыми (рис. 6). Но при более строгом анализе выясняется, что само понятие площади нуждается в обосновании, а потому нельзя опираться на него, решая вопросы существования первообразной и определенного интеграла.
Далее выясним, что для многочисленных приложений наиболее целесообразен именно второй подход. Кроме того, мы увидим, что для широкого класса функций оба подхода приводят к одному и тому же результату.
Оценки определенных интегралов
что и требовалось доказать.
Двойное неравенство (1) дает лишь весьма грубую оценку для значения определенного интеграла. Например, на отрезке значения функции заключены между 1 и 25, а потому имеют место неравенства
Но по аддитивному свойству определенного интеграла сумма интегралов по всем частям отрезка равна интегралу по этому отрезку, т. е.
Например, если разбить отрезок на 10 равных частей, каждая из которых имеет длину 0,4, то на частичном отрезке выполняется неравенство
Чтобы получить еще более точную оценку интеграла, надо разбить отрезок не на 10, а, скажем, на 100 или 1000 частей и сосчитать соответствующие суммы. Разумеется, данный интеграл проще вычислить с помощью первообразной:
Но если выражение для первообразной нам неизвестно, то неравенства (2) дают возможность оценить значение интеграла снизу и сверху.
Определенный интеграл как разделяющее число
Это определение естественно, так как при изменении направления промежутка интегрирования все разности меняют знак, а тогда меняют знаки и суммы Дарбу и, тем самым, разделяющее их число, т.е. интеграл.
Так как при все обращаются в нуль, то положим
Мы получили два определения понятия определенного интеграла: как разности значений первообразной и как разделяющего числа для сумм Дарбу. Эти определения в наиболее важных случаях приводят к одному и тому же результату:
Свойства нижних и верхних сумм Дарбу
Для того чтобы данное ранее определение интеграла имело смысл, надо доказать, что множество верхних сумм Дарбу действительно расположено справа от множества нижних сумм Дарбу.
Доказательство. Рассмотрим некоторое разбиение отрезка :
что и требовалось доказать.
Лемма 2. От добавления новой точки деления нижняя сумма Дарбу не может уменьшиться, а верхняя сумма не может увеличиться.
Слагаемому первоначальной нижней суммы Дарбу в новой нижней сумме Дарбу соответствуют два слагаемых:
Оценим снизу сумму полученных слагаемых:
Перейдем к сравнению сумм Дарбу для любых двух разбиений.
Лемма 3. Ни одна нижняя сумма Дарбу не превосходит любой верхней суммы Дарбу (хотя бы отвечающей другому разбиению отрезка ).
Из леммы 3 следует, что числовое множество нижних сумм Дарбу лежит левее числового множества верхних сумм Дарбу.
Определённый интеграл
Смотреть что такое «Определённый интеграл» в других словарях:
Определённый интеграл — Определённый интеграл аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая область в множестве задания этой функции (функционала).… … Википедия
определённый интеграл — см. Интегральное исчисление. * * * ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, см. Интегральное исчисление (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ) … Энциклопедический словарь
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ — см. Интегральное исчисление … Естествознание. Энциклопедический словарь
Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия
Интеграл (значения) — Интеграл (см. также Первообразная, Численное интегрирование, Интегрирование по частям) математический оператор: Определённый интеграл Неопределённый интеграл различные определения интегралов: Интеграл расширение понятия суммы Интеграл Ито… … Википедия
Интеграл — (от лат. integer целый) одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости… … Большая советская энциклопедия
Интеграл Даниэля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниэлем (Daniell) в 1918 году в его… … Википедия
Определенный интеграл — Определённый интеграл как площадь фигуры В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как… … Википедия
Интеграл Даниеля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниелем (англ.) в 1918 году в его… … Википедия
Первообразная
Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого 
Операция нахождения первообразной функции f(x), называется интегрированием.
Неопределенный интеграл
Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.
Дифференциал-произвольное, бесконечно малое приращение переменной величины.
Свойства неопределённого интеграла
Таблица основных неопределённых интегралов
В виде

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.
Определённый интеграл
Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].
Общий вид определённого интеграла:
где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал
Свойства определённого интеграла: см. св-ва определённого интеграла.
Определённый интеграл вычисляется по формуле Ньютона –Лейбница:
Применение определённого интеграла:
1. Нахождение площади криволинейной трапеции
2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е
Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.
Решение:
3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.
Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.
Решение:
Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.
Глава II. Определенный интеграл



Практическое занятие 2.1. Линейный интеграл. Формула Ньютона-Лейбница. Замена переменной. Интегрирование по частям
2.1.1. Формула Ньютона-Лейбница
Существует несколько типов определенных интегралов в зависимости от вида области интегрирования (лекция 3.6).
Если интегрируемая функция задана на точках прямой, интеграл называют линейным. Он равен пределу интегральной суммы, т.е. числу, его записывают:
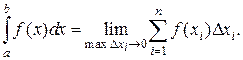

Интервал от а до b называют интервалом интегрирования. При вычислении линейного интеграла пользуются формулой Ньютона-Лейбница, согласно которой линейный интеграл равен приращению любой из первообразных для функций f(x) на интервале интегрирования [a; b]:
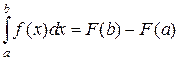
Разность значений функции F(x) часто записывают так:
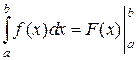
где знак 
Найдем несколько простых интегралов с помощью полученной формулы.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Пример 5.
До сих пор считалось, что нижний предел в линейном интеграле 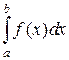
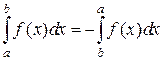
Далее следует отметить, что вычисление линейного интеграла с помощью неопределенного по формуле Ньютона-Лейбница на практике не всегда возможно. Во-первых, первообразная может не выражаться через известные элементарные функции, т.е. не берется соответствующий неопределенный интеграл, либо первообразная не выражается через известные неэлементарные (специальные) функции. Во-вторых, найденная первообразная может оказаться очень громоздкой. И, наконец, функция, которую надо проинтегрировать, может быть задана не формулой, а например, таблицей значений или графиком. Во всех этих случаях линейный интеграл вычисляют приближенно с помощью численного интегрирования.
Задачи для самостоятельного решения. Вычислить интегралы.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
2.1.2. Замена переменной интегрирования в линейном интеграле
Переход к новой переменной интегрирования в определенном интеграле проводят по формуле:
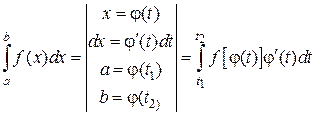
где функция х = φ(t) – должна быть дифференцируемой, а обратная t = ψ(х) – однозначной. Подынтегральное выражение в формуле (2.1.4) преобразуется так же, как в неопределенном интеграле. Однако очень важно подчеркнуть, что одновременно с преобразованием подынтегрального выражения, следует пересчитать пределы интегрирования, так как у новой переменной t будут другие границы изменения. Эти границы находят из уравнений:
Уравнения получают путем подстановки х = α, х = b в функцию х = ψ(t). Возвращаться к старой переменной x, как это было в случае неопределенного интеграла, здесь не нужно.
Пример 6. Вычислить интеграл: 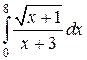
Чтобы избавиться от корня, возьмем его за новую переменную:
В приведенном примере новые пределы интегрирования 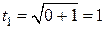
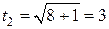
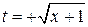
t = ψ(х) – однозначна.
Пример 7. Вычислить интеграл
Как и в предыдущем примере за новую переменную возьмем квадратный корень.
В результате интеграл сводится к двум табличным:
Задачи для самостоятельного решения. Вычислить интеграл.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
2.1.3. Интегрирование по частям в линейном интеграле
Нахождение первообразной методом интегрирования по частям в линейном интеграле проводят по той же формуле, что и в неопределенном интеграле:
Разница заключается лишь в том, что для линейного интеграла находят не саму первообразную, а её приращение на интервале интегрирования [α,b].
Пример 8. Вычислить интеграл 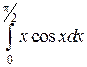
Решение. Разобьем на части подынтегральное выражение
В данном случае соответствующий неопределенный интеграл берется. Значение линейного интеграла найдено по формуле Ньютона-Лейбница.
Задачи для самостоятельного решения. Вычислить интегралы.
1.
2.
3.
4.
5.
6.
2.1.4. Приближенное вычисление линейного интеграла
Приближенное вычисление определенных интегралов по формулам прямоугольников, трапеций и Симпсона подробно рассмотрено в лекции 3.8. Вывод этих формул дан, исходя из геометрического смыла линейного интеграла, равного площади криволинейной трапеции.
В случае возрастающей функции на интервале [a,b], формула левых прямоугольников, дающая значение интеграла снедостатком, имеет вид:
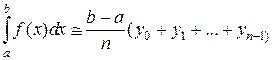
где у0, у1, …, уn-1 – значения подынтегральной функции в начале каждого частичного интервала.
Если значения функций берутся в конце частичных интервалов, то приближенное значение интеграла получают с избытком:
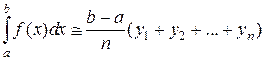
Формула правых прямоугольников. Обе формулы имеют сравнительно большую погрешность (первого порядка малости). Так для левых прямоугольников главный член погрешности на частичном интервале равен
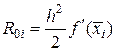
Суммирование по всему интервалу [а, b] дает общую ошибку
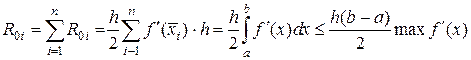
Если учесть, что 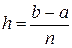
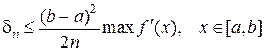
При уменьшении в два раза числа разбиений интервала [а, b] абсолютная ошибка возрастает также в два раза.
По сравнению с формулами (2.1.4.1) и (2.1.4.2) более точным является метод средних прямоугольников, т.е. когда значения функции f(х) вычисляют в срединах каждого частного интервала:
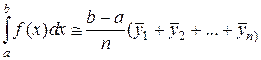
При этом верхняя граница абсолютной ошибки равна
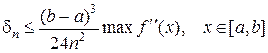
Если число точек (узлов) увеличить в два раза, точность формулы (2.1.4.3) улучшится в четыре раза. В самом деле
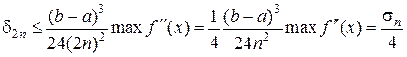
Однако, если подынтегральная функция f(х) определяется из эксперимента в дискретном наборе узлов, то метод средних прямоугольников применить нельзя из-за отсутствия значений f(х) в средних точках 
По формуле трапеций приближенное значение линейного интеграла равно
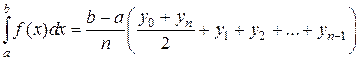
Абсолютная ошибка, которая получается при вычислении интеграла по этой формуле, не превосходит величины:
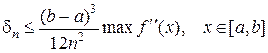
Однако, она в два раза больше по сравнению с методом средних прямоугольников. В обоих случаях, чем больше n – тем меньше ошибка.
На практике обычно трудно определить mах f» (х), поэтому для оценки верхней границы погрешности пользуются другим выражением:
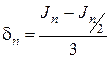
Формулу (2.1.4.6) получают следующим образом. Уменьшим число разбиений интервала [а, b] в два раза: n/2 и найдем, во сколько раз возрастет верхняя граница ошибки
Точное значение линейного интеграла можно записать двумя способами
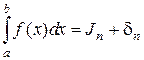
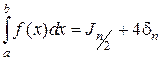
где Jn – приближенное значение интеграла, полученное при разбиении интервала [а, b] на n частей; Jn/2– приближенное значение интеграла при разбиении на 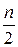
Откуда следует, что
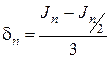
Формула парабол (формула Симпсона) имеет вид:
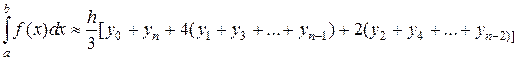
Формулу (2.1.4.9) называют формулой парабол или формулой Симпсона. Верхняя граница погрешности при вычислениях интеграла по этой формуле равна
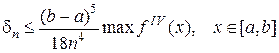
Погрешность имеет четвертый порядок малости. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. На практике в случае формулы Симпсона для δn. Пользуется таким равенством:
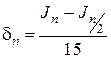
Его получают аналогично равенству (2.1.4.6). При уменьшении числа разбиений интервала [а, b] в два раза, верхняя граница ошибки возрастает в 16 раз:
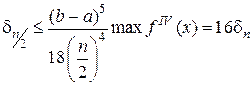
поэтому 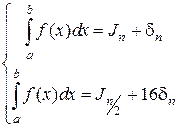
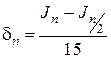
Пример. Вычислишь по формуле Ньютона-Лейбница и приближенно линейный интеграл:
полученные результаты сравнить
1. Найдем точное значение данного интеграла по формуле Ньютона-Лейбница:
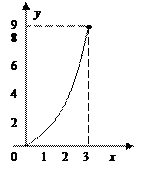 |
| Рис. 2.1.4.1 |
2. Построим график подынтегральной функции (рис. 2.1.4.1).
Разобьем интервал b – а = 3 – 1 = 2 на десять частей, т.е. n = 10
Вычислим значения подынтегральной функции в точках: х0 = 1; х1= 1,2; х2 = 1,4 и т.д., а также в срединах частичных интервалов. Результаты занесем в таблицу.
| № | хi | у = х 2 | № | хi | у = х 2 | № |  |  |
| х0 | у0 = 1 | х0 | ||||||
| х1 | 1,2 | у1 = 1,44 | 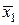 | 1,1 | 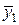 =1,21 =1,21 | |||
| х2 | 1,4 | у2 = 1,96 | х1 | 1,4 | 1,96 | 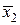 | 1,3 | 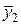 = 1,69 = 1,69 |
| х3 | 1,6 | у3 = 2,56 | 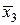 | 1,5 | 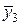 = 2,25 = 2,25 | |||
| х4 | 1,8 | у4 = 3,24 | х2 | 1,8 | 3,24 | 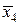 | 1,7 | 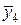 = 2,89 = 2,89 |
| х5 | у5 = 4 | 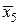 | 1,9 | 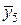 = 3,61 = 3,61 | ||||
| х6 | 2,2 | у6 = 4,84 | х3 | 2,2 | 4,84 | 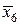 | 2,1 | 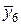 = 4,41 = 4,41 |
| х7 | 2,4 | у7 = 5,76 | 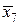 | 2,3 | 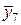 = 5,29 = 5,29 | |||
| х8 | 2,6 | у8 = 6,76 | х4 | 2,6 | 6,76 | 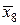 | 2,5 | 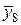 = 6,25 = 6,25 |
| х9 | 2,8 | у9 = 7,84 | 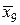 | 2,7 | 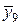 = 7,29 = 7,29 | |||
| х10 | у10 = 9 | х5 | 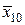 | 2,9 | 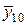 = 8,41 = 8,41 | |||
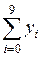 =39,4; =39,4; 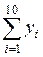 = 47,4 = 47,4 | 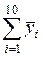 =43,3 =43,3 |
По формуле левых прямоугольников (с недостатком) находим
По формуле правых прямоугольников (с избытком) получим
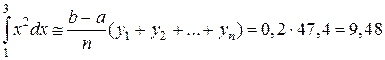
Результаты сильно отличаются от истинного значения, т.е. вычисления проведены с большой погрешностью. Найдем приближенное значение данного интеграла по формуле средних прямоугольников
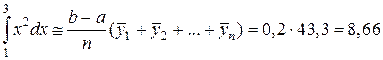
Результат весьма близкий к истинному.
Для сравнения вычислим приближенное значение данного интеграла по формулам трапеций и Симпсона.
По формуле трапеций для n = 10 с шагом h = 0,2 находим
По формуле трапеций для 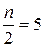
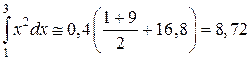
Верхняя граница абсолютной ошибки равна
И, наконец, по формуле Симпсона для n = 10; h = 0,2
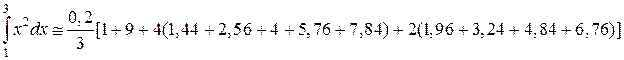
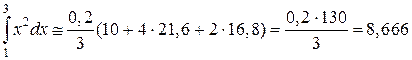
Как и следовало ожидать, самую высокую точность вычислений дает формула парабол (Симпсона), а затем формула средних прямоугольников.
Вычислить самостоятельно интеграл.
1) по формуле Ньютона-Лейбница;
2) по формуле левых и правых прямоугольников с шагом h = 0,1;
3) по формуле средних прямоугольников;
4) по формулам трапеций и Симпсона;
5) найти верхнюю границу погрешности для вычислений по формулам трапеций и Симпсона.
Практическое занятие 2.2. Несобственные интегралы I и II рода
Определенный линейный интеграл существует, если выполнены два условия, а именно:
1. интервал интегрирования конечен;
2. подынтегральная функция в интервале интегрирования нигде не обращается в бесконечность.
Такие определенные интегралы называют интегралами в собственном смысле этого слова, или собственными. Однако иногда приходится иметь дело с интегралами, у которых нарушено одно из этих условий. Они получили название несобственных.
2.2.1. Линейные интегралы с бесконечными пределами (I рода)
Дан определенный линейный интеграл:
у которого f(x) – непрерывна на всей числовой оси 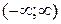
называют несобственными интегралами первого рода, или интегралами с бесконечными границами.
Если эти пределы равны конечному числу, то в таких случаях говорят, что несобственные интегралы первого рода сходятся.
Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся (не существуют).
Несобственные интегралы первого рода с одной бесконечной границей находят по формулам:
Поскольку под знаком пределов стоят определенные интегралы с конечными границами, их можно вычислять по формуле Ньютона-Лейбница (при условии, что соответствующий неопределенный интеграл берется), а затем найти предел полученного выражения.
Вычисление интеграла, у которого обе границы бесконечны, сводят к вычислению суммы двух несобственных интегралов с одной бесконечной границей:
Вычислить несобственные интегралы:
Пример 1.
Пример 2.
Функция sin5b при 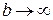
Пример 3.
Пример 4.
Вычислим каждый из двух интегралов с одной бесконечной границей:
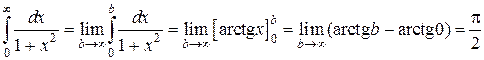
Складывая найденные значения двух несобственных интегралов, получим:
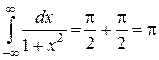
Данный интеграл сходится.
Пример 5.
Пример 6.
Пример 7.
Разложим подынтегральную функцию на простейшие дроби.
Приводя простейшие дроби к общему знаменателю и освобождаясь от него получим:
Приравняем числовые коэффициенты при одинаковых степенях х:
| х 2 | 0 = A + C; A = –C |
| х 1 | 0 = A + B; A = –B |
| х 0 | 1 = В |
Заменим подынтегральную функцию суммой простейших дробей:
Применяя формулу Ньютона-Лейбница и вычисляя предел, окончательно получаем:
Пример 8.
Сделаем замену переменной интегрирования:
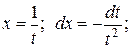
Задачи для самостоятельного решения. Вычислить интегралы.
2.2.2. Линейные интегралы от разрывных функций, или несобственные интегралы второго рода
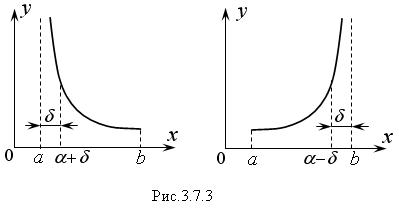
Рассмотрим интеграл 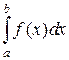
|
Изолируем точки бесконечного разрыва δ – окрестностью и рассмотрим такие пределы:
Эти пределы называют несобственными интегралами второго рода. Разрыв в одном из концов интервала обозначен символом «–».
В случае конечных пределов, говорят, что несобственные интегралы сходятся.
Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся.
Подынтегральная функция может иметь бесконечный разрыв в промежуточной точке х = с интервала [α,b]. Интеграл от такой функции разбивают на два несобственных интеграла второго рода:
Определение определённого интеграла и его свойства
Пусть функция у = ƒ(x) определена и непрерывна на отрезке [а, b]. Разобьём отрезок [а, b] на n частей точками а = х0 0, не зависящий от способа разбиения отрезка [а, b] на части, ни от выбора точек ξi в них.
Теорема существования определённого интеграла: Если функция у = ƒ(x) непрерывна на отрезке [а, b], то она интегрируема на нем.
Свойства определенного интеграла
Аддитивность по области интегрирования
Аддитивность по функции
Теорема «о среднем»
Перестановка пределов интегрирования
Производная от интеграла с переменным верхним пределом интегрирования
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Смотреть что такое «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ» в других словарях:
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интегральное исчисление … Большой Энциклопедический словарь
Определенный интеграл — Определённый интеграл как площадь фигуры В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как… … Википедия
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интеграл … Математическая энциклопедия
ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… … Экономический словарь
ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь
Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия
ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия
интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика
интеграл Джоуля I2t — интеграл Джоуля Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента … Справочник технического переводчика
Интеграл — [integral]. Есть два различных понятия неопределенный И. и определенный И. Говорят, что функция f(x) имеет неопределенный И. ∫f(x)dx, если существует такая функция F(x), что ее производная dF(x)/dx равна исходной функции f(x). Функция F(x)… … Экономико-математический словарь
Как определить определенные интегралы от нуля, константы и с доказательством
С целью повышения точности решения практических задач, как в строительстве, так и экономике иногда нужен более «мощный» инструмент, который давал бы ответ на нестандартные условия. К примеру, вычисление площади покрытия не традиционной формы (половины параболы), изготовление конструкций, удаляемая или застраивая площадь и многое другое. Таким инструментом является именно интеграл, рамки исчисления которого, задает сам пользователь. Приведем примеры вычислений определенного интеграла с доказательством его свойств,
Значение понятия
Рисунок 1. Общий вид криволинейной трапеции.
Невзирая на теоретическое обоснование, сразу дадим более четкое понятие этого термина. Определенным интегралом считается площадь криволинейной трапеции, которая за основания принимает снизу – ось абсцисс, а снизу саму функцию. Более наглядно это изображено на рисунке 1. Такое трактование называется геометрическим, и более понятно, чем остальные.
В более классическом определении, численное выражение интеграла является величина какой – либо первообразной на выбранном и ограниченном промежутке (отрезке). На практике значение такого приращения может быть, как больше, так и меньше нуля. В отношении значения площади данный вопрос зависит от того, в какой полуплоскости находится кривая (верхней или нижней), такой и будет знак (на практике его значение отбрасывают). В численном выражение наше определение имеет такую формулу:
Опираясь на вышеуказанную формулу можем утверждать, что определенный интеграл представляет собой разность первообразной в крайних точках выбранного интервала (такой подход к определению называют формула Ньютона – Лейбница).
Это интересно! Первый признак равенства треугольников: доказательство
Свойства интеграла Римана на отрезке
Для того, чтобы безошибочно находить площади «кривых» трапеций, рассмотрим основные «приёмы», которые существенно облегчат этот процесс.
Основные свойства:
Площадь трапеции в отдельно взятой точке равна нулю. Формулой можно записать так:
Если функция определена между точками a и b, то справедливо следующее равенство:
Если под интегральные функции w(x) и t(x) определены на отрезке [k,c] и не имеют точек разрыва, нет таких точек в которых бы функции не имели значения, то справедливо равенство:
В случае если первообразная функция определена (вычислима в каждой точке) и пределы интегрирования лежат на отрезке [k,c], тогда под интегральную функцию можно записать в следующем виде:
Функция j(x) интегрируема на отрезке [a,d], только в том случае, когда сам отрезок [a,d] принадлежит большему отрезку [k,c].
Отметим, что данный список не включает в себя все свойства определенного интеграла и имеет продолжение. Указанные «хитрости» являются наиболее распространенными приемами, однако применять их нужно убедившись в их «работоспособности».
Для большей наглядности найдем значение интеграла, пределы интегрирования которого расположены на отрезке [3,5] для под интегральной
Решение. Согласно условию задачи, имеем следующую под интегральную функцию определенную на промежутке
Можем получить следующее:
Допустим, что вместо функции с переменной x, находится 0 (такой вариант тоже считают функцией и совпадает с осью абсцисс). Тогда пытаясь найти определённый интеграл от постоянной получим:
Выходит, что если в под интегральной функции стоит нуль, то и первообразная, на каком бы отрезке не была определена, тоже будет равна нулю.
В случае, если требуется найти интеграл от константы, то следующее решение дает пример решения любого многочлена:
Откуда делаем вывод, что если требуется определить интеграл от нуля, то его значение (можно даже не расписывать) равен нулю, а если интеграл от числа, то разницу между концами отрезка нужно умножить на число под знаком интеграла.
Важно! Во время решения задач подобного плана, часто приходится комбинировать указанные приемы, для уменьшения сложности задания. Но используя такие переходы, не стоит забывать, что интегральная сумма всегда должна совпадать с первоначальной. Всегда проверяйте отрезок, на котором собираетесь интегрировать, иначе полученное значение будет отличаться от действительного.
«Умные» определения интегрирования непрерывной функции
Для удачного поиска первообразной необходимо знание и понимание таких понятий как: интегральная сумма, пределы интегрирования и общее понимание определения «интеграл функции».
Границы на определенном отрезке
Суть данного понятия заключается в том, что пределы интегрирования функции (это тот самый отрезок, который заранее определяется), это максимально граничные значения кривой, в которых она еще «действительна». К примеру, наша под интегральная определена на отрезке от 2 до 4. Это означает что мы можем найти первообразную для функции в точке со значением 2.000000001 (практически 2) и 3.9999999 (почти 4), но если пределы интегрирования больше (меньше), то все дальнейшие значения бессмысленны. Изобразим это на рисунке 2, где предложены возможные продолжения кривой.
Рисунок 2.Возможное поведение функции за пределами интегрирования.
Такое требование к пределам вытекает из того, что нам не известно определена ли функция за этими пределами или нет. А также то, как она поведет себя за своими пределами. По сути, функция верхнего основания говорит о том, как располагаются точки на указанном отрезке (вполне возможно, что за пределами это уже будет функция Дирихле, то есть будут точки разрыва). В своей сущности под понятием «интеграл функции» имеется в виду процесс поиска первообразной (первородной), из которой эта самая функция при поиске производной и получилась. Еще проще – действие обратное поиску производной.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
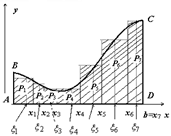
Сумма
Представим, что дана произвольная трапеция, верхнее основание которой произвольная кривая. Если из образованной фигуры, образовать похожие внутри первоначальной. То получим бесконечное множество таких трапеций, у каждой из которых функция, определяющая верхнее основание, будет одинакова. Далее на каждом нижнем основании (малые отрезки) возьмём какую угодно точку, умножим значение функции в этой самой точке на разницу в основании, то получим площадь этой трапеции. Сумма площадей всех этих трапеций, будет равна площади изначально данной. Это будет интегральная сумма.
Рисунок 3. Сумма интегралов.
Математически это будет выглядеть так:
Для более понятного восприятия рекомендуем присмотреться к рисунку 3.
Полезное видео: что такое определенный интеграл?
Полезное видео: как решить определенный интеграл?
Вывод
При решении обычных задач или примеров данные определения редко имеют существенное значение. Но не лишним будет их правильное понимание и применение перед тем, как начнется само решение. Как правило, определенные интегралы, представляемые на ЕГЭ, все соответствуют данным критерием. Однако, теория проверяется тоже, и не стоит её отбрасывать ввиду сложности понимания.
Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Смотреть что такое «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ» в других словарях:
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — (definite integral) Интеграл функции, вычисляемый на интервале, ограниченном верхним и нижним пределами. Если первой производной функции F(х) является f(x), то определенный интеграл f(x) равен F(x)+k. Определенный интеграл f(x) на интервале с… … Экономический словарь
Определенный интеграл — Определённый интеграл как площадь фигуры В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как… … Википедия
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интеграл … Математическая энциклопедия
ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… … Экономический словарь
ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь
Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия
ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия
интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика
интеграл Джоуля I2t — интеграл Джоуля Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента … Справочник технического переводчика
Интеграл — [integral]. Есть два различных понятия неопределенный И. и определенный И. Говорят, что функция f(x) имеет неопределенный И. ∫f(x)dx, если существует такая функция F(x), что ее производная dF(x)/dx равна исходной функции f(x). Функция F(x)… … Экономико-математический словарь
Свойства определенного интеграла
Данная статья подробно рассказывает об основных свойствах определенного интеграла. Они доказываются при помощи понятия интеграла Римана и Дарбу. Вычисление определенного интеграла проходит, благодаря 5 свойствам. Оставшиеся из них применяются для оценивания различных выражений.
Основные свойства определенного интеграла
Из определения Римана это выражение является равносильным.
Доказательство свойства определенного интеграла аналогично предыдущему:
Доказательство основывается на свойстве Дарбу: если у имеющегося разбиения отрезка произвести добавление точек, тогда нижняя сумма Дарбу не будет уменьшаться, а верхняя не будет увеличиваться.
Благодаря утверждению знаем, что интегрирование допустимо. Данное следствие будет использовано в доказательстве других свойств.
Первая формула среднего значения
Первая формула среднего значения в обобщенной форме
Вторая формула среднего значения
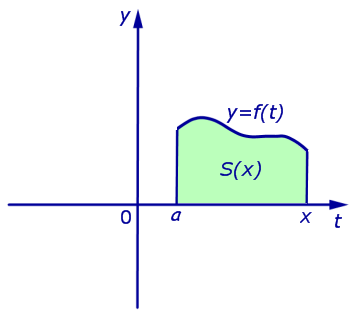
Определенный интеграл как площадь криволинейной трапеции
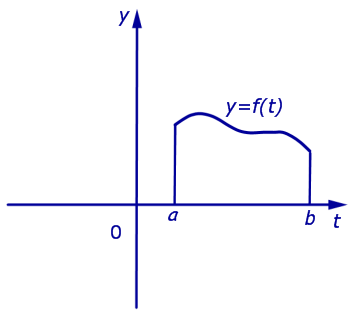
Пусть y = f (t) – непрерывная на отрезке [a, b] функция, принимающая только положительные значения.
Определение 1. Фигуру, ограниченную графиком функции y = f (t) сверху, отрезком [a, b] снизу, а справа и слева отрезками прямых t = a и t = b (рис. 2), называют криволинейной трапецией.
Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции f (t) в пределах от a до b и обозначают
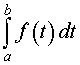 | (1) |
Формула (1) читается так: «Интеграл от a до b от функции f (t) по dt »
Определение 3. В формуле (1) функцию f (t) называют подынтегральной функцией, переменную t называют переменной интегрирования, отрезок [a, b] называют отрезком интегрирования, число b называют верхним пределом интегрирования, а число a – нижним пределом интегрирования.
Производная от определенного интеграла по верхнему пределу
Если обозначить S (x) площадь криволинейной трапеции, ограниченной с боков отрезками прямых t = a и t = x (рис. 3),
то будет справедлива формула
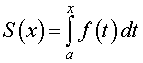 | (2) |
Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.
Другими словами, справедлива формула
Доказательство. Из формулы (2) следует, что
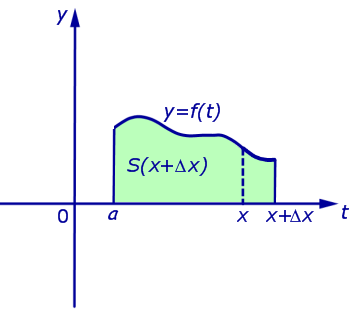
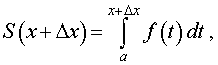 | (3) |
где через Δx обозначено приращение аргумента x (рис. 4)
Из формул (3) и (2) получаем, что
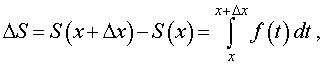 | (4) |
где через ΔS обозначено приращение функции S (x), соответствующее приращению аргумента Δx (рис. 5)
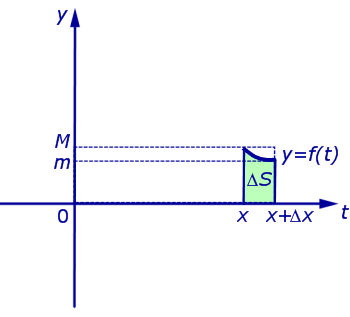
Если ввести обозначения
(см. раздел «Наибольшее и наименьшее значение функции на отрезке»), то можно заметить, что выполнено неравенство
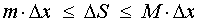 | (5) |
смысл которого заключается в том, что площадь криволинейной трапеции, изображенной на рисунке 5, не может быть меньше, чем площадь прямоугольника с основанием Δx и высотой m, и не может быть больше, чем площадь прямоугольника с основанием Δx и высотой M.
Из неравенства (5) следует, что
В силу непрерывности функции y = f (t) выполнено равенство
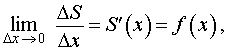 | (6) |
что и завершает доказательство теоремы 1.
Теорема Ньютона-Лейбница. Если F (x) – любая первообразная функции f (x), то справедливо равенство
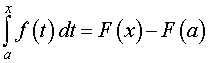 | (7) |
| S (x) = F (x) + c | (8) |
Воспользовавшись равенством (8), из формулы (2) получаем, что
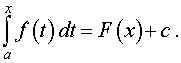 | (9) |
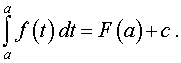 | (10) |
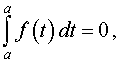 | (11) |
Из формул (10) и (11) следует, что
и формула (9) принимает вид
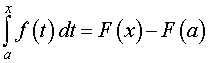
что и завершает доказательство теоремы Ньютона-Лейбница.
Замечание 1. Формулу (7) часто записывают в виде
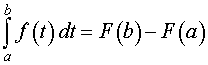 | (12) |
и называют формулой Ньютона-Лейбница.
Замечание 2. Для правой части формулы Ньютона-Лейбница часто используют обозначение
Замечание 4. Все определения и теоремы остаются справедливыми не только в случае положительных непрерывных функций f (x), но и для гораздо более широкого класса функций, имеющих произвольные знаки и интегрируемых по Риману, однако этот материал уже выходит за рамки школьного курса математики.
Примеры решения задач
Задача 1. Найти площадь фигуры, ограниченной линиями
Решение. Рассматриваемая фигура является криволинейной трапеции (рис. 6)
Ответ.
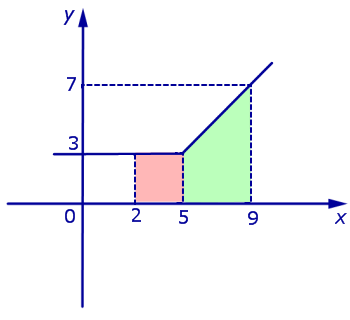
Задача 2. График функции y = f (x) изображен на рисунке 7.
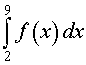 | (13) |
Решение. Интеграл (13) равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f (x), ограниченной снизу осью абсцисс Ox и ограниченной с боков отрезками прямых x = 2 и x = 9. Криволинейная трапеция состоит из квадрата, раскрашенного на рисунке 7 розовым цветом, и трапеции, раскрашенной на рисунке 7 зеленым цветом. Площадь квадрата равна 9, а площадь трапеции равна 20. Таким образом, интеграл (13) равен 29.
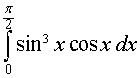 | (14) |
Решение. Поскольку одной из первообразных подынтегральной функции интеграла (14) является функция
то в соответствии с формулой Ньютона-Лейбница получаем
Ответ.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Смотреть что такое «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ» в других словарях:
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — (definite integral) Интеграл функции, вычисляемый на интервале, ограниченном верхним и нижним пределами. Если первой производной функции F(х) является f(x), то определенный интеграл f(x) равен F(x)+k. Определенный интеграл f(x) на интервале с… … Экономический словарь
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интегральное исчисление … Большой Энциклопедический словарь
Определенный интеграл — Определённый интеграл как площадь фигуры В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как… … Википедия
ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… … Экономический словарь
ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь
Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия
ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия
интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика
интеграл Джоуля I2t — интеграл Джоуля Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента … Справочник технического переводчика
Интеграл — [integral]. Есть два различных понятия неопределенный И. и определенный И. Говорят, что функция f(x) имеет неопределенный И. ∫f(x)dx, если существует такая функция F(x), что ее производная dF(x)/dx равна исходной функции f(x). Функция F(x)… … Экономико-математический словарь
Математический анализ
Записки лекций
24.1 Интеграл Римана
24.1.1 Интеграл и площадь
Чтобы начать отвечать на этот вопрос, нужно подумать о том, что вообще такое «площадь». Мы знаем, что площадь прямоугольника — это произведение его длины и ширины. Мы также знаем (считаем это аксиомой или частью определения), что если у нас есть две фигуры, и мы складываем из них третью «без нахлёста», то площадь новой фигуры равна сумме площадей исходных фигур. И ещё, что если у нас есть две равные фигуры (то есть такие, которые можно положить друг на друга так, чтобы они совпали), то их площади равны. Из этих трёх правил можно вывести много других. Например, прямоугольник разбивается своей диагональю на два равных прямоугольных треугольника, и значит площадь каждого из них вдвое меньше площади прямоугольника, и равна половине произведения катетов. Произвольные треугольник разбивается высотой на два прямоугольных, откуда легко вывести, что его площадь равна половине произведения высоты на основания. Более сложные многоугольники можно разбивать на треугольники и находить их площади таким образом. Так мы определяем площади довольно широкого класса фигур — но далеко не всех. Что делать, если мы имеем дело не с многоугольником, а фигурой, ограниченной какой-то «кривой» линией, не состоящей из прямолинейных отрезков? Такую фигуру нельзя разбить на прямоугольники или треугольники. Однако, её можно приблизить более простыми фигурами с известными площадами, добиться того, чтобы эти приближения становились всё лучше и лучше, и перейти к пределу. Именно таким образом определяется интеграл Римана.
24.1.2 Разбиения и интегральные суммы
Чтобы это сформулировать аккуратно, придётся ввести несколько новых понятий.
24.1.3 Определенный интеграл как предел
Можно записать, что
Обозначается интеграл таким образом:
24.2 Свойства определённого интеграла
24.2.1 Интегрируемые и неинтегрируемые функции
Не все функции интегрируемы. Например, функция Дирихле
Трудно описать множество всех интегрируемых функций, однако для наших целей важно сказать, что функции из некоторых важных для нас классов таким свойством обладают.
Непрерывность является достаточным условием интегрируемости, но не является необходимым — например, кусочно-непрерывные функции, чьи разрывы являются скачками, тоже интегрируемы. Чуть позже мы обсудим это подробнее.
24.2.2 Интеграл как площадь с учётом знака
24.2.3 Линейность и интегрирование неравенств
24.2.4 Интегрируемость и ограниченность
Более формальное доказательство выглядит следующим образом. Пусть
24.2.5 Аддитивность интеграла
Также можно, заметить, что если мы в определнии интегральной суммы разрешим разбиения, идущие «справа налево», и перенумеруем элементы какого-то разбиения с конца
Интеграл, методы интегрирования
Неопределенный интеграл
Узнайте что такое первообразная и неопределенный интеграл, запомните основные свойства.
Запомните формулы из таблицы интегралов, научитесь применять их вместе со свойствами неопределенного интеграла при интегрировании.
Научитесь выполнять интегрирование подведением под знак дифференциала, разберите решения характерных примеров.
Освойте метод интегрирования по частям, запомните формулу и разберитесь в тонкостях введения новых функций u и v.
Познакомьтесь с интегрированием простейших дробей всех четырех видов и нахождением интегралов дробно рациональных функций, рассмотрите приведенные решения примеров.
Показан принцип интегрирования с использованием рекуррентных формул, показаны примеры нахождения неопределенных интегралов степеней синуса и косинуса.
Разобраны способы нахождения интегралов от различных иррациональных функций, показаны примеры с подробным пояснением хода решения.
Узнайте основные принципы интегрирования тригонометрических функций, в том числе метод с использованием универсальной тригонометрической подстановки.
Определенный интеграл
Разберитесь что такое определенный интеграл, узнайте определения определенного интеграла Римана, Дарбу и Ньютона-Лейбница, а также необходимое условие интегрируемости функции.
Познакомьтесь со свойствами определенного интеграла и их доказательством, с их помощью вычисляются определенные интегралы.
Узнайте геометрический смысл определенного интеграла, связанный с площадью криволинейной трапеции, разберите примеры вычисления площади.
Дана формула Ньютона-Лейбница, показан ее вывод, разобрано как с помощью формулы Ньютона-Лейбница вычисляются определенные интегралы, приведены решения примеров.
Приложения
Узнайте что такое площадь фигуры, какими свойствами она обладает и какие фигуры являются квадрируемыми.
Запомните формулу для нахождения площади фигуры, ограниченной линиями в прямоугольной системе координат, разберите решения характерных примеров.
Выведена формула для нахождения площади криволинейного сектора, на примерах разобрано как находятся площади фигур в полярных координатах (кардиоиды, лемнискаты, улитки Паскаля).
Научитесь через определенный интеграл вычислять площадь фигуры, которая ограничена линией, заданной параметрическими уравнениями, разберите решения примеров.
Приближенное вычисление
Посмотрите как приближенно может быть вычислен определенный интеграл методом прямоугольников, разберите алгоритм, способ оценки погрешности и решения примеров.
Представлены формулы метода трапеций для приближенного вычисления определенного интеграла, приведены решения примеров и оценка погрешности численного метода.
Познакомьтесь с численным интегрированием методом Симпсона (парабол), рассмотрите решение примера и сравнение погрешности метода парабол с погрешностями других методов.