Что такое прямоугольник
Что такое прямоугольник
Прямоугольник
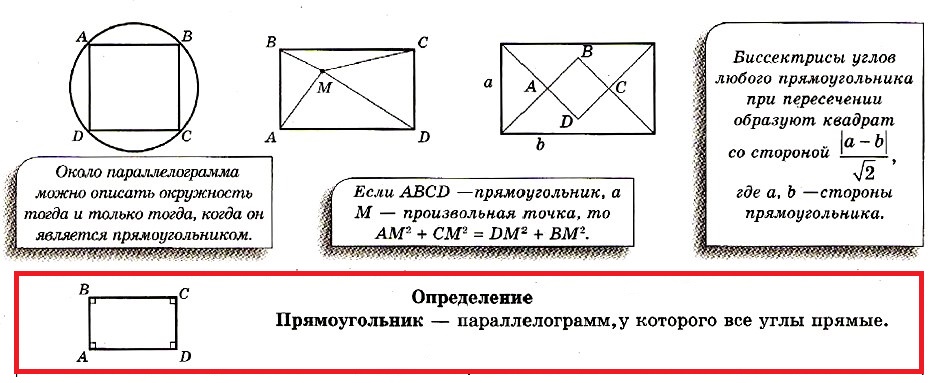
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу теоремы о сумме углов многоугольника) также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360° — прямоугольников не существует.
Содержание
Свойства
Площадь и стороны
Диагонали прямоугольника
Признаки
См. также
Планигон
Полезное
Смотреть что такое «Прямоугольник» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это.
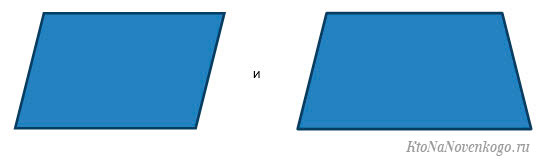
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
Диагонали прямоугольника
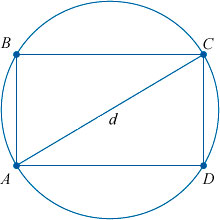
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
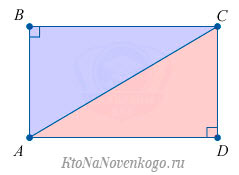
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Частным случаем прямоугольника является квадрат.
Свойства прямоугольника
1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.
Помимо этого:
2. Стороны прямоугольника являются его высотами.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Признаки параллелограмма
Параллелограмм является прямоугольником, если выполняется любое из условий:
1. Диагонали параллелограмма равны.
2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.
3. Все углы параллелограмма равны.
Площадь прямоугольника
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Прямоугольник
Смотреть что такое «Прямоугольник» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК
— четырехугольник, у к-рого все углы прямые. П. является параллелограммом.
Смотреть что такое «ПРЯМОУГОЛЬНИК» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
Что такое прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Свойства и признаки прямоугольника
Свойства прямоугольника:
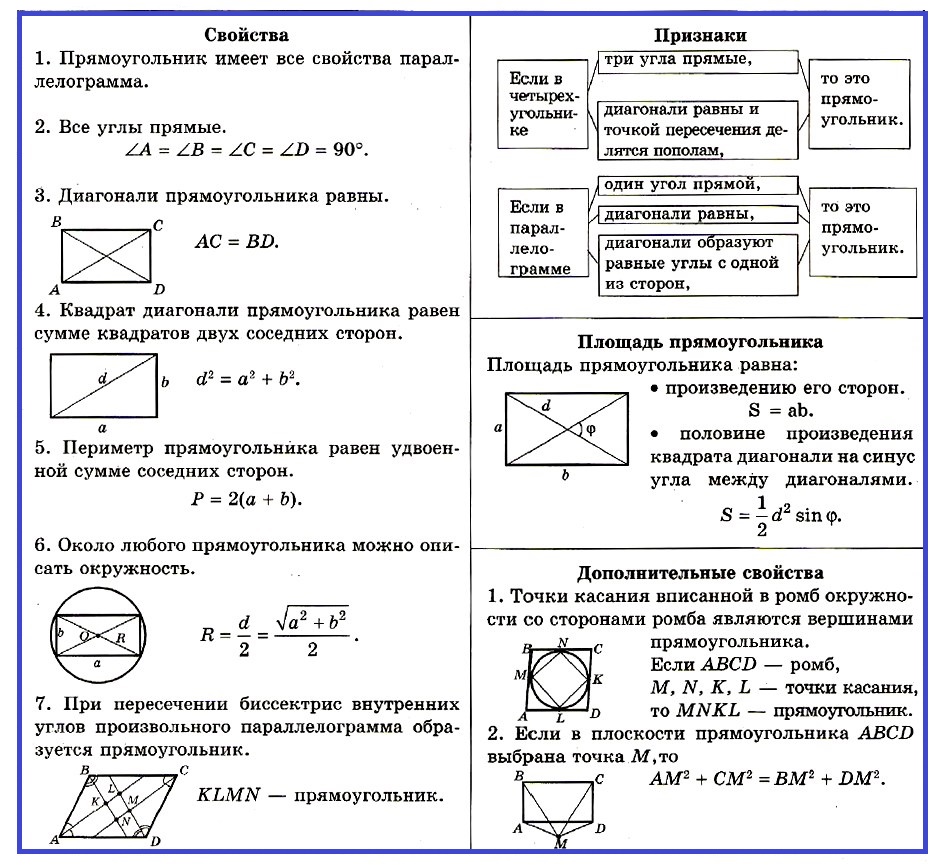
1. Прямоугoльник имеет все свойства параллелограмма.
2. Все углы прямые.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух соседних сторон.
5. Периметр прямоугольника равен удвоенной сумме соседних сторон.
6. Около любого прямоугольника можно описать окружность.
7. При пересечении биссектрис внутренних углов произвольного параллелограмма образуется прямоугoльник.
Признаки прямоугольников:
Если в четырехугольнике три угла прямые.
Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам.
Если в параллелограмме один угол прямой, диагонали равны.
Если в параллелограмме диагонали образуют равные углы с одной из сторон.
Это конспект по теме «Прямоугольник и его свойства». Выберите дальнейшие действия:
Прямоугольник
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.
Свойства прямоугольника
1. Прямоугольник — это параллелограмм.
2. Противоположные стороны равны.
AB = CD,\enspace BC = AD
3. Противоположные стороны параллельны.
AB \parallel CD,\enspace BC \parallel AD
4. Прилегающие стороны перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB
5. Диагонали прямоугольника равны.
Следовательно, \triangle ABD = \triangle DCA по двум катетам ( AB = CD и AD — совместный).
Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы Пифагора.
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника.
\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD
8. Точка пересечения диагоналей делит их пополам.
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности.
10. Сумма всех углов равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^
11. Все углы прямоугольника прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^
12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника.
13. Вокруг прямоугольника всегда можно описать окружность.
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна 180^
\angle ABC = \angle CDA = 180^<\circ>,\enspace \angle BCD = \angle DAB = 180^
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).
Прямоугольник, свойства, признаки и формулы
Прямоугольник, свойства, признаки и формулы.
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.
Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
Рис. 7. Прямоугольник
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
9. Диагонали прямоугольника делятся точкой пересечения пополам.
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
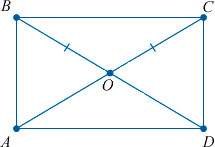
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):




Формула диагонали прямоугольника:

Формулы периметра прямоугольника:
Формулы площади прямоугольника:
Формула радиуса окружности, описанной вокруг прямоугольника:

Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Прямоугольник
Прямоугольник — это выпуклый многоугольник. Прямоугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
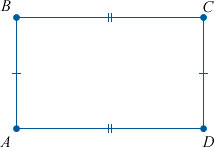
В тексте прямоугольники обозначаются четырьмя прописными латинскими буквами, стоящими при вершинах — ABCD.
У прямоугольников противоположные стороны параллельны и равны:
В прямоугольнике ABCD точки A, B, C и D — это вершины прямоугольника, отрезки AB, BC, CD и DA — стороны. Углы, образованные сторонами, называются внутренними углами или просто углами прямоугольника.
Главное отличие прямоугольников от остальных четырёхугольников — четыре прямых внутренних угла:
Свойства диагоналей
Отрезки, соединяющие противолежащие вершины прямоугольника, называются диагоналями.
Отрезки AC и BD — диагонали, O — точка пересечения диагоналей.
В любом прямоугольнике можно провести всего две диагонали. Они обладают следующими свойствами:
Квадрат — прямоугольник, у которого все стороны равны. Диагонали квадрата обладают всеми свойствами диагоналей прямоугольника. Также диагонали квадрата имеют и дополнительных свойства:
прямоугольник
Смотреть что такое «прямоугольник» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК
Смотреть что такое «ПРЯМОУГОЛЬНИК» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
Значение слова «прямоугольник»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.
ПРЯМОУГО’ЛЬНИК, а, м. (геом.). Четырехугольник, в к-ром все углы прямые.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
прямоуго́льник
1. геометр. четырёхугольник, у которого все четыре угла прямые ◆ Противоположные стороны прямоугольника равны. ◆ Любой прямоугольник является параллелограммом.
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: керосинка — это что-то нейтральное, положительное или отрицательное?
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 36. Прямоугольник
Перечень вопросов, рассматриваемых в теме:
— знакомство с прямоугольником.
Глоссарий по теме:
Прямоугольник – четырёхугольник, у которого все углы прямые.
Геометрия – раздел математики, изучающий пространственные отношения и формы.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2. – 8-е изд. – М.: Просвещение, 2017. – с.14-15.
2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2. – 7-е изд., дораб. – М.: Просвещение, 2017. – с.23.
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры. У всех четыре угла. Можно заметить, что одна из фигур имеет только прямые углы. Это прямоугольник
Рассмотрим фигуру с одним прямым углом. Это треугольник.
Рассмотрим фигуру с прямыми углами. Это четырехугольник.
Четырехугольник относится к группе прямоугольников.
Определить, что углы прямые можно с помощью треугольника, прикладывая его в каждый угол: угол D, затем угол С, затем угол В, и угол А.
Значит, фигуры, у которых все углы прямые, можно назвать прямоугольники.
У прямоугольника четыре стороны. Вертикально расположена ширина, обычно меньшая сторона.
Но прямоугольниками можно назвать только те четырёхугольники, у которых все углы прямые.
Горизонтально расположена длина, обычно большая сторона.
Обратите внимание на написание слова: длина.
Запомните, как это слово пишется!
1. Найдите на картинке прямоугольники и определите их количество.
Прямоугольников на этой картинке 10.
2. Найдите прямоугольники и запишите их номера:

Виды прямоугольников и их описание
Прямоугольник — что это за фигура
Прямоугольник — четырехугольник (параллелограмм), у которого все углы прямые. Также прямоугольником может являться квадрат.
Признаки прямоугольника
Параллелограмм является прямоугольником, если выполняется хотя бы одно условие:
Свойства прямоугольника
Каждый прямоугольник является параллелограммом, а значит, что все свойства параллелограмма присущи и прямоугольнику.
Кроме того, есть свойства характерные именно для этой геометрической фигуры.
Площадь прямоугольника
S A B C D = a × b
S A B C D = 1 2 d 2 sin i
Периметр прямоугольника
Периметр прямоугольника равен сумме произведения удвоенной ширины и удвоенной длины прямоугольника: P A B C D = 2 a + 2 b
Примеры решения задач
Дано: ABCD — прямоугольник; B D = 14 ; ∠ B D C = 30 °
Ответ: 21
Дано: ABCD — прямоугольник; AU — биссектриса; AB=12
Найти: P A B C D
Свойства прямоугольника

Средняя оценка: 4.1
Всего получено оценок: 861.
Средняя оценка: 4.1
Всего получено оценок: 861.
Прямоугольник уникален своей простотой. На основе этой фигуры ученики начинают познавать основы геометрии. Поэтому в старших классах теряются, не зная основных свойств и признаков прямоугольника, напрасно считая эту фигуру излишне простой.
Прямоугольник
Определение прямоугольника известно с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что же такое параллелограмм?
Несмотря на заковыристое название, эта фигура столь же проста, как и прямоугольник. Параллелограмм это выпуклый четырехугольник, стороны которого попарно равны и параллельны.
В определении обязательно выделять слово выпуклый. Поскольку выпуклые и невыпуклые четырехугольники четко разделяются в геометрии. Причем невыпуклые фигуры вообще не изучаются в школьном курсе математики, так как они куда более непредсказуемы в своих свойствах.
Прямоугольник это частный случай параллелограмма. При этом существуют и другие частные случаи параллелограмма, например, ромб; и еще один особенный частный случай прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.
Свойства прямоугольника
Свойства прямоугольника можно разбить на две группу: свойства параллелограмма и свойства прямоугольника.
Свойства параллелограмма:
Свойства прямоугольника:
Признаки прямоугольника
У прямоугольника всего три основных признака:
Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве.
В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.
Что мы узнали?
Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника. Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма.
Прямоугольник и квадрат
Определение
Прямоугольник – это параллелограмм, у которого один угол прямой.
Таким образом, прямоугольник обладает всеми свойствами параллелограмма:
\(\sim\) противоположные стороны попарно равны;
\(\sim\) диагонали точкой пересечения делятся пополам.
Теоремы: свойства прямоугольника
1) Все углы прямоугольника прямые.
2) Диагонали прямоугольника равны.
Доказательство
Следствие
Теоремы: признаки прямоугольника
1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
2) Если в выпуклом четырехугольнике все углы прямые, то он – прямоугольник.
Доказательство
1) Пусть в параллелограмме \(ABCD\) диагонали равны.
2) Рассмотрим четырехугольник \(ABCD\) :
Определение
Два эквивалентных определения квадрата:
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат – это ромб, у которого один угол прямой.
Свойства квадрата
Так как квадрат является прямоугольником и ромбом, то он обладает всеми свойствами прямоугольника и ромба:
\(\sim\) Все углы квадрата равны \(90^\circ\) ;
\(\sim\) Все стороны квадрата равны;
\(\sim\) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Какой четырёхугольник называется прямоугольником

Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.
Признаки и свойства прямоугольника
Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.
Формулы для вычисления длины сторон
В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).
Это интересно: в геометрии луч это что такое, основное понятие.
Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:
Это интересно: как сравнить два отрезка способы с примерами.
Периметр и площадь

Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:
Диагонали прямоугольника
В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:
Это интересно: как обозначается площадь, примеры для вычисления.
Применяются следующие формулы для расчёта длины диагонали:
Определение и свойства квадрата
Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.
Четырёхугольник называют квадратом в следующих случаях:
К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:
Приведём часто используемые формулы для 
Примеры вопросов и задач
Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.
Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?
Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.
Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?
Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.
Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.
Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.
Вопрос 2. У прямоугольника все стороны равны или нет?
Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.
Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.

Геометрические фигуры. Прямоугольник. Свойства прямоугольника.
Прямоугольник — параллелограмм с прямыми углами, равными 90 градусам и двумя противоположными равными сторонами.
В евклидовой геометрии для того, чтобы четырехугольник оказался прямоугольником, нужно, чтобы хотя бы 3 угла были прямыми. Четвертый угол также будет равен 90°, исходя из теоремы о сумме углов многоугольников. В неевклидовой геометрии, если сумма углов четырёхугольника больше или меньше 360 градусов, такой четырехугольник не может быть прямоугольником.
Разница в прямоугольниках лишь в отношении длинной стороны к короткой, в то время как каждый из четырех углов прямой (равен 90°).
Свойства прямоугольника.
Кроме параллелограмма прямоугольником могут быть еще квадрат и ромб.
— Стороны прямоугольника – это его же высоты.
— Квадрат диагонали прямоугольника = сумме квадратов 2-х смежных сторон (из теоремы Пифагора).
— Вокруг всякого прямоугольника легко описать окружность, при этом диагональ прямоугольника будет равной с диаметром окружности, которая описана (тогда радиус окружности будет равен полудиагонали прямоугольника).
— У противоположных сторон прямоугольника одинаковая длина, т.е. стороны равны:
— Противолежащие стороны прямоугольника параллельны друг другу:
— Прилегающие стороны прямоугольника перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
— Каждый их четырех углов прямоугольника прямой:
— Сумма углов прямоугольника составляет 360°:
— Диагонали прямоугольника имеют одинаковые длины:
— Сумма квадратов диагонали прямоугольника равна сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
— Все диагонали прямоугольника делят прямоугольник на 2 одинаковые фигуры (если конкретнее, на прямоугольные треугольники).
— Диагонали прямоугольника пересекаются, деля друг друга на 2 равные части:
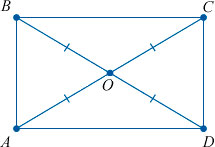
AO = BO = CO = DO = d/2
— Точку пересечения диагоналей называют центром прямоугольника, кроме того она есть центр описанной окружности.
— Диагональ прямоугольника есть диаметр окружности описанной.
— Около прямоугольника легко описать окружность, т.к. сумма противолежащих углов равна 180°:
Понятие прямоугольника. Что такое прямоугольник
Время на чтение: 14 минут
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d |
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
Стороны прямоугольника
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
| b = d cos | β |
| 2 |
Диагональ прямоугольника
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
2. Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
5. Формула диагонали прямоугольника через диаметр описанной окружности:
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
Периметр прямоугольника
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
Площадь прямоугольника
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
2. Формула площади прямоугольника через периметр и любую сторону:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
Окружность описанная вокруг прямоугольника
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство. Диагонали прямоугольника равны.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Разделы: Начальная школа
Тема : Виды четырехугольников. Прямоугольник
Тип урока – комбинированный.
Вид урока – дидактическая игра.
Методы и приемы обучения: диалогический и эвристический методы:
Ход урока
Сегодня на уроке мы с вами совершим путешествие в удивительную страну Геометрию :
– Кто знает, что в переводе с греческого обозначает слово “геометрия”?
“Гео” – земля, “метрия” – измерение.
Наука эта появилась в Греции.
Сопровождать нас будет в нашем путешествии (учитель показывает сказочного героя) удивительный герой – волшебник.
– Всех вас он зашифровал, и вы будете путешествовать под зашифрованными номерами.
– Кто узнал его? (Старик Хоттабыч.)
– Кто написал книжку “Старик Хоттабыч”? (Лагин.)
Старик Хоттабыч очень старый волшебник и его знания устарели, поэтому он пришел к вам на урок и хочет узнать, что же сейчас изучают современные дети. Помогите волшебнику разобраться.
– Что изображено на доске? (Геометрические фигуры.)
– Определите на какие 2 группы вы могли бы разделить эти геометрические фигуры? (Треугольники и четырехугольники.)
Заполните карточку №1. Укажите номера треугольников и четырехугольников. Все дети указывают в карточке номера.
В это время 2 ученика фиксируют ответы на доске.
– Укажите во второй карточке номера треугольников по углам (тупоугольный, прямоугольный, остроугольный) и по сторонам (равносторонний и равнобедренный).
Работу выполняют по вариантам, а потом обмениваются карточками и осуществляют взаимопроверку в парах.
1) Сегодня мы с нашим героем познакомимся с видами четырёхугольников, а именно; с прямоугольником, научимся его чертить и выделять среди других фигур Т.к. треугольников и четырёхугольников в геометрии много. Вот как выглядят некоторые из них:
– Какие из них вы уже знаете?
Дети называют те виды, которые знают.
– Что общего у этих фигур, что их объединяет в одну группу?
(4 стороны, 4 угла, 4 вершины.)
– А чем один вид отличается от другого? (Длинами сторон и особенностями углов.)
Учитель обращает внимание детей на таблицу и говорит определения.
2) Помогите Хоттабычу из ряда четырехугольников найти похожие (1 3 5).
– Как называются углы у фигур 1, 3, 5? (Прямые.)
– А как бы вы назвали эти фигуры? (Прямоугольники.)
– Попробуйте сказать, что же такое прямоугольник?
Прямоугольник – геометрическая фигура, у которой все углы прямые и противоположные стороны равны.
– Назовите вершины у прямоугольника АВСД? (А, В, С, Д – вершины.)
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
\(\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD \)
8. Точка пересечения диагоналей делит их пополам
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности
У прямоугольников противоположные стороны параллельны и равны:
Свойства диагоналей
В любом прямоугольнике можно провести всего две диагонали. Они обладают следующими свойствами:
ПРЯМОУГОЛЬНИК
Смотреть что такое «ПРЯМОУГОЛЬНИК» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК
— четырехугольник, у к-рого все углы прямые. П. является параллелограммом.
Смотреть что такое ПРЯМОУГОЛЬНИК в других словарях:
ПРЯМОУГОЛЬНИК
см. Фигуры геометрические.
ПРЯМОУГОЛЬНИК
четырёхугольник, у которого все углы прямые. П. является Параллелограммом.
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
прямоугольник м. 1) Четырехугольник, у которого все углы прямые (в геометрии). 2) То, что формой напоминает такой четырехугольник.
ПРЯМОУГОЛЬНИК
прямоугольник м. мат.rectangle
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
Прямоугольник — см. Фигуры геометрические.
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
1) Орфографическая запись слова: прямоугольник2) Ударение в слове: прямоуг`ольник3) Деление слова на слоги (перенос слова): прямоугольник4) Фонетическа. смотреть
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков.Словарь бизнес-терминов.Академик.ру.200. смотреть
ПРЯМОУГОЛЬНИК
прямоугольник сущ.муж.неод. (1)ед.род.югу от предместия, в виде прямоугольника, которого диагональ плотно примыкает к Куре.Пр14.
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
Ударение в слове: прямоуг`ольникУдарение падает на букву: оБезударные гласные в слове: прямоуг`ольник
ПРЯМОУГОЛЬНИК
(в блок-схемах) bar, (блок-схемы) box, rectangle* * *прямоуго́льник м.rectangleСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
Rzeczownik прямоугольник m Matematyczny prostokąt m
ПРЯМОУГОЛЬНИК
(2 м); мн. прямоуго/льники, Р. прямоуго/льниковСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник.Синон. смотреть
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
м мат re(c)tângulo mСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно па. смотреть
ПРЯМОУГОЛЬНИК
(напр. в блок-схемах) bar* * *rectangleСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
прямоугольникמַלבֵּן ז’* * *מלבןСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
— термин, используемый в анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник.Синонимы: квад. смотреть
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
прямоуго’льник, прямоуго’льники, прямоуго’льника, прямоуго’льников, прямоуго’льнику, прямоуго’льникам, прямоуго’льник, прямоуго’льники, прямоуго’льником, прямоуго’льниками, прямоуго’льнике, прямоуго’льниках. смотреть
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
-а, м. Четырехугольник, в котором все углы прямые.Синонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
m.rectangleСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
1) rectangle2) rectangular box– рабочий прямоугольникСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
сущ. муж. родамат.прямокутник
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
мdikdörtgenСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
четырёхугольник, у к-рого все углы прямые. Синонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
м.rectangle mСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
мRechteck nСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающихся на графике в прямоугольник.
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
长方形 chángfāngxíng, 矩形 jǔxíngСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
прямоугольникСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
м.rectangle- прямоугольник текучести
ПРЯМОУГОЛЬНИК
термин, используемый в анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник.
ПРЯМОУГОЛЬНИК
термин, используемый в анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник.
ПРЯМОУГОЛЬНИК
ПРЯМОУГОЛЬНИК
м. Rechteck n прямоугольный — rechteckig; rechtwinklig (имеющий один прямой угол) прямоугольный треугольник — rechtwinkliges Dreieck.
ПРЯМОУГОЛЬНИК
прямоугольник м Rechteck n 1aСинонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
прямоугольник = м. rectangle; прямоугольный rectangular; прямоугольный треугольник right-angled triangle.
ПРЯМОУГОЛЬНИК
вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков.
ПРЯМОУГОЛЬНИК
[rectangle]: Смотри также: — прямоугольник — квадрат — прямоугольник — гладкая бочка
ПРЯМОУГОЛЬНИК
м. rettangolo m Итальяно-русский словарь.2003. Синонимы: квадрат, параллелограмм, четырехугольник
ПРЯМОУГОЛЬНИК
Основные геометрические фигуры
О чем эта статья:
7 класс, 8 класс
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это это часть плоскости, которая лежит внутри окружности.
Окружность — это граница круга.
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Свойства прямоугольника – определение, основные признаки
Прямоугольник уникален своей простотой. На основе этой фигуры ученики начинают познавать основы геометрии. Поэтому в старших классах теряются, не зная основных свойств и признаков прямоугольника, напрасно считая эту фигуру излишне простой.
Прямоугольник
Определение прямоугольника известно с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что же такое параллелограмм?
Несмотря на заковыристое название, эта фигура столь же проста, как и прямоугольник. Параллелограмм это выпуклый четырехугольник, стороны которого попарно равны и параллельны.
В определении обязательно выделять слово выпуклый. Поскольку выпуклые и невыпуклые четырехугольники четко разделяются в геометрии. Причем невыпуклые фигуры вообще не изучаются в школьном курсе математики, так как они куда более непредсказуемы в своих свойствах.
Рис. 1. Выпуклые четырехугольники
Прямоугольник это частный случай параллелограмма. При этом существуют как другие частные случаи параллелограмма, например, ромб; так и другие частные случаи прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.
Свойства прямоугольника
Свойства прямоугольника можно разбить на две группу: свойства параллелограмма и свойства прямоугольника.
Свойства параллелограмма:
Рис. 2. Свойства параллелограмма
Свойства прямоугольника:
Признаки прямоугольника
У прямоугольника всего три основных признака:
Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве.
В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.
Что мы узнали?
Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника. Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма.
что такое прямоугольник в геометрии определение
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Частным случаем прямоугольника является квадрат.
Свойства прямоугольника
1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.
Помимо этого:
2. Стороны прямоугольника являются его высотами.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Признаки параллелограмма
Параллелограмм является прямоугольником, если выполняется любое из условий:
1. Диагонали параллелограмма равны.
2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.
3. Все углы параллелограмма равны.
Площадь прямоугольника
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Прямоугольник, свойства, признаки и формулы
Прямоугольник, свойства, признаки и формулы.
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.
Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
Рис. 7. Прямоугольник
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
9. Диагонали прямоугольника делятся точкой пересечения пополам.
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):




Формула диагонали прямоугольника:

Формулы периметра прямоугольника:
Формулы площади прямоугольника:
Формула радиуса окружности, описанной вокруг прямоугольника:

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Прямоугольник
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.
Свойства прямоугольника
1. Прямоугольник — это параллелограмм.
2. Противоположные стороны равны.
AB = CD,\enspace BC = AD
3. Противоположные стороны параллельны.
AB \parallel CD,\enspace BC \parallel AD
4. Прилегающие стороны перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB
5. Диагонали прямоугольника равны.
Следовательно, \triangle ABD = \triangle DCA по двум катетам ( AB = CD и AD — совместный).
Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы Пифагора.
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника.
\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD
8. Точка пересечения диагоналей делит их пополам.
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности.
10. Сумма всех углов равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^
11. Все углы прямоугольника прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^
12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника.
13. Вокруг прямоугольника всегда можно описать окружность.
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна 180^
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).
Геометрические фигуры. Прямоугольник. Свойства прямоугольника.
Прямоугольник — параллелограмм с прямыми углами, равными 90 градусам и двумя противоположными равными сторонами.
В евклидовой геометрии для того, чтобы четырехугольник оказался прямоугольником, нужно, чтобы хотя бы 3 угла были прямыми. Четвертый угол также будет равен 90°, исходя из теоремы о сумме углов многоугольников. В неевклидовой геометрии, если сумма углов четырёхугольника больше или меньше 360 градусов, такой четырехугольник не может быть прямоугольником.
Разница в прямоугольниках лишь в отношении длинной стороны к короткой, в то время как каждый из четырех углов прямой (равен 90°).
Свойства прямоугольника.
Кроме параллелограмма прямоугольником могут быть еще квадрат и ромб.
— Стороны прямоугольника – это его же высоты.
— Квадрат диагонали прямоугольника = сумме квадратов 2-х смежных сторон (из теоремы Пифагора).
— Вокруг всякого прямоугольника легко описать окружность, при этом диагональ прямоугольника будет равной с диаметром окружности, которая описана (тогда радиус окружности будет равен полудиагонали прямоугольника).
— У противоположных сторон прямоугольника одинаковая длина, т.е. стороны равны:
— Противолежащие стороны прямоугольника параллельны друг другу:
— Прилегающие стороны прямоугольника перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
— Каждый их четырех углов прямоугольника прямой:
— Сумма углов прямоугольника составляет 360°:
— Диагонали прямоугольника имеют одинаковые длины:
— Сумма квадратов диагонали прямоугольника равна сумме квадратов сторон:
— Все диагонали прямоугольника делят прямоугольник на 2 одинаковые фигуры (если конкретнее, на прямоугольные треугольники).
— Диагонали прямоугольника пересекаются, деля друг друга на 2 равные части:
AO = BO = CO = DO = d/2
— Точку пересечения диагоналей называют центром прямоугольника, кроме того она есть центр описанной окружности.
— Диагональ прямоугольника есть диаметр окружности описанной.
— Около прямоугольника легко описать окружность, т.к. сумма противолежащих углов равна 180°:


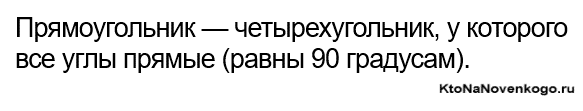


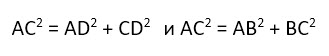
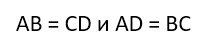
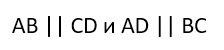

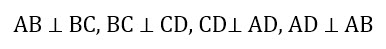
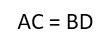
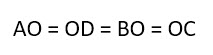

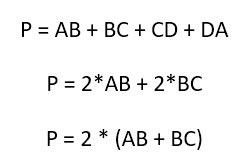
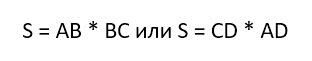














.png)






.png)






















































































