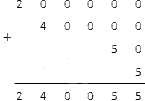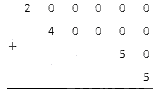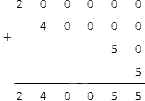Что такое сумма разрядных слагаемых
Что такое сумма разрядных слагаемых
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок № 9. Разрядные слагаемые. Сравнение многозначных чисел
Перечень вопросов, рассматриваемых в теме:
— как можно представит многозначное число(больше 1000) в виде разрядных слагаемых?
— как можно записать большое число в виде суммы разрядных слагаемых?
Глоссарий по теме:
Многозначные числа – это целые числа, при записи которых нужно использовать несколько цифр (знаков).
Разряд — это место (позиция), на котором в записи числа.
Сравнение чисел – определение большего или меньшего числа.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.26
2. Математика в вопросах и заданиях. 4 кл.: тетрадь для самостоятельной работы №1/О.А. Захарова, Е.П. Юдина.- М: Академкнига /Учебник, 2016.- с.19-21
3. Готовимся к Всероссийской проверочной работе. Математика. Рабочая тетрадь 4 класс/ под.ред. Г.С. Ковалевой – М.; Просвещение, 2017. – с. 7
Теоретический материал для самостоятельного изучения
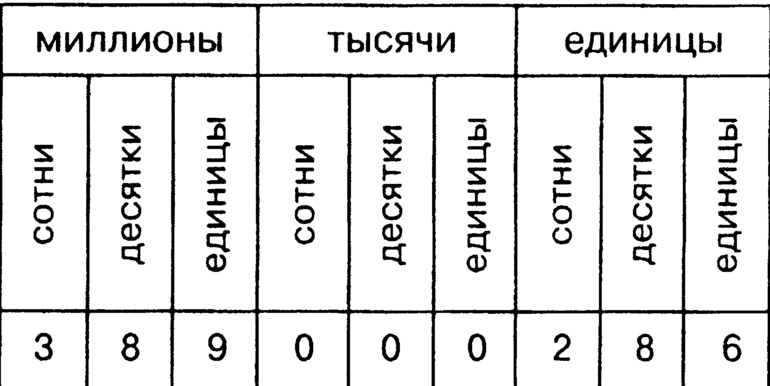
Рассмотрим шестизначное число 721 948. Оно содержит 7 сотен тысяч 2 десятка тысяч 1 тысячу 9 сотен 4 десятка и 8 единиц.
Запись данного числа в таблице разрядов выглядит так:
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок № 9. Разрядные слагаемые. Сравнение многозначных чисел
Перечень вопросов, рассматриваемых в теме:
— как можно представит многозначное число(больше 1000) в виде разрядных слагаемых?
— как можно записать большое число в виде суммы разрядных слагаемых?
Глоссарий по теме:
Многозначные числа – это целые числа, при записи которых нужно использовать несколько цифр (знаков).
Разряд — это место (позиция), на котором в записи числа.
Сравнение чисел – определение большего или меньшего числа.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.26
2. Математика в вопросах и заданиях. 4 кл.: тетрадь для самостоятельной работы №1/О.А. Захарова, Е.П. Юдина.- М: Академкнига /Учебник, 2016.- с.19-21
3. Готовимся к Всероссийской проверочной работе. Математика. Рабочая тетрадь 4 класс/ под.ред. Г.С. Ковалевой – М.; Просвещение, 2017. – с. 7
Теоретический материал для самостоятельного изучения
Рассмотрим шестизначное число 721 948. Оно содержит 7 сотен тысяч 2 десятка тысяч 1 тысячу 9 сотен 4 десятка и 8 единиц.
Запись данного числа в таблице разрядов выглядит так:
Разрядные слагаемые
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Например, число « 64 » состоит из 6 десятков и 4 единиц.
Числа « 60 » и « 4 » называются разрядными слагаемыми.
Представление числа в виде:
356 = 3 сотни + 5 десятков + 6 единиц = 3 · 100 + 5 · 10 + 6 = 300 + 50 + 6
8 092 = 8 тысяч + 0 сотен + 9 десятков + 2 единицы = 8 · 1 000 + 0 · 100 + 9 · 10 + 2 = 8 000 + 90 + 2
Числа 1, 10, 100, 1000 и т.д. — называются разрядными единицами. Так, 1 — это единица разряда единиц; 10 — единица разряда десятков; 100 — единица разряда сотен и т.д.
Часто в заданиях требуется не только разложить число на разрядные слагаемые, но и определить количество всех единиц какого-либо разряда. В этом случае советуем сделать подробный разбор числа.
Пример подробного разбора многозначного числа « 2 038 479 » (два миллиона тридцать восемь тысяч четыреста семьдесят девять).
Советуем обратить особое внимание на данную тему, так как умение раскладывать числа на разрядные слагаемые поможет вам при устном счёте и решении примеров с многозначными числами.
Для проверки своих результатов вы также можете воспользоваться нашим калькулятором разложения числа на разрядные слагаемые онлайн.
Что такое разрядные слогаемые
Ответ или решение 2
Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.
Примеры разложения чисел на разрядные слагаемые:
Более сложный пример с большим числом разрядов:
Определим, что такое разрядные слагаемые
Разрядные слагаемые – это сумма чисел с разной разрядностью.
Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.
Числа 1, 10, 100, 1000 и так далее – это разрядные единицы.
Запишем разделение разрядных слагаемых:
Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы.
Примеры разрядных слагаемых:
Рассмотрим пример определения разрядных слагаемых числа 92586
Сначала, разложим число 92586 на разрядные слагаемые и получим:
92 586 = 90000 + 2000 + 500 + 80 + 6 = 9 * 10 000 + 2 * 1 000 + 5 * 100 + 8 * 10 + 6 * 1.
Запишем, из чего состоит число 92 586:
Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.
Разрядные слагаемые числа
Сумма разрядных слагаемых
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Как это делается, видно из следующего примера: число 999 состоит из 9 сотен, 9 десятков и 9 единиц, поэтому:
999 = 9 сотен + 9 десятков + 9 единиц = 900 + 90 + 9.
Числа 900, 90 и 9 — разрядные слагаемые. Разрядное слагаемое — это количество единиц в данном разряде.
Сумму разрядных слагаемых также можно записать следующим образом:
999 = 9 · 100 + 9 · 10 + 9 · 1.
Числа, на которые выполняется умножение (1, 10, 100, 1000 и т. д.), называются разрядными единицами. Так, 1 — это единица разряда единиц, 10 — единица разряда десятков, 100 — единица разряда сотен и т. д. Числа, которые умножаются на разрядные единицы выражают количество разрядных единиц.
Запись любого числа в виде:
12 = 1 · 10 + 2 · 1 или 12 = 10 + 2
называется разложением числа на разрядные слагаемые (или суммой разрядных слагаемых).
Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц.
Пример 1. Запишите числа в виде суммы разрядных слагаемых: 3278, 5031, 3700.
1) 3278 = 3 · 1000 + 2 · 100 + 7 · 10 + 8 · 1 = 3000 + 200 + 70 + 8;
2) 5031 = 5 · 1000 + 0 · 100 + 3 · 10 + 1 · 1 = 5000 + 30 + 1;
3) 3700 = 3 · 1000 + 7 · 100 + 0 · 10 + 0 · 1 = 3000 + 700.
Обратите внимание, что разрядные единицы могут быть записаны в виде степени числа 10:
1) 3278 = 3 · 10 3 + 2 · 10 2 + 7 · 10 1 + 8 · 1;
2) 5031 = 5 · 10 3 + 0 · 10 2 + 3 · 10 1 + 1 · 1 = 5 · 10 3 + 3 · 10 1 + 1;
Пример 2. Записать число, представленное в виде суммы разрядных слагаемых:
а) 3 · 10 2 + 2 · 10 + 7 = 300 + 20 + 7 = 327;
б) 5 · 10 3 + 0 · 10 2 + 4 · 10 + 1 = 5000 + 40 + 1 = 5041;
в) 8 · 10 2 + 0 · 10 + 5 = 800 + 5 = 805;
г) 1 · 10 3 + 6 · 10 2 + 7 · 10 = 1000 + 600 + 70 = 1670.
Калькулятор разложения числа на разрядные слагаемые
Сумма разрядных слагаемых натурального числа
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Получаем:
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Сумма разрядных слагаемых
О чем эта статья:
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
Число 35 состоит из 3 десятков и 5 единиц
35 = 3 десятка + 5 единиц = 30 + 5
30 — разрядное слагаемое; 5 — разрядное слагаемое.
Число 86 состоит из 8 десятков и 6 единиц
86 = 8 десятков + 6 единиц = 80 + 6
80 — разрядное слагаемое; 6 — разрядное слагаемое.
Число 356 состоит из 3 сотен, 5 десятков и 6 единиц
356 = 3 сотни + 5 десятков + 6 единиц = 300 + 50 + 6
300, 50, 6 — разрядные слагаемые.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
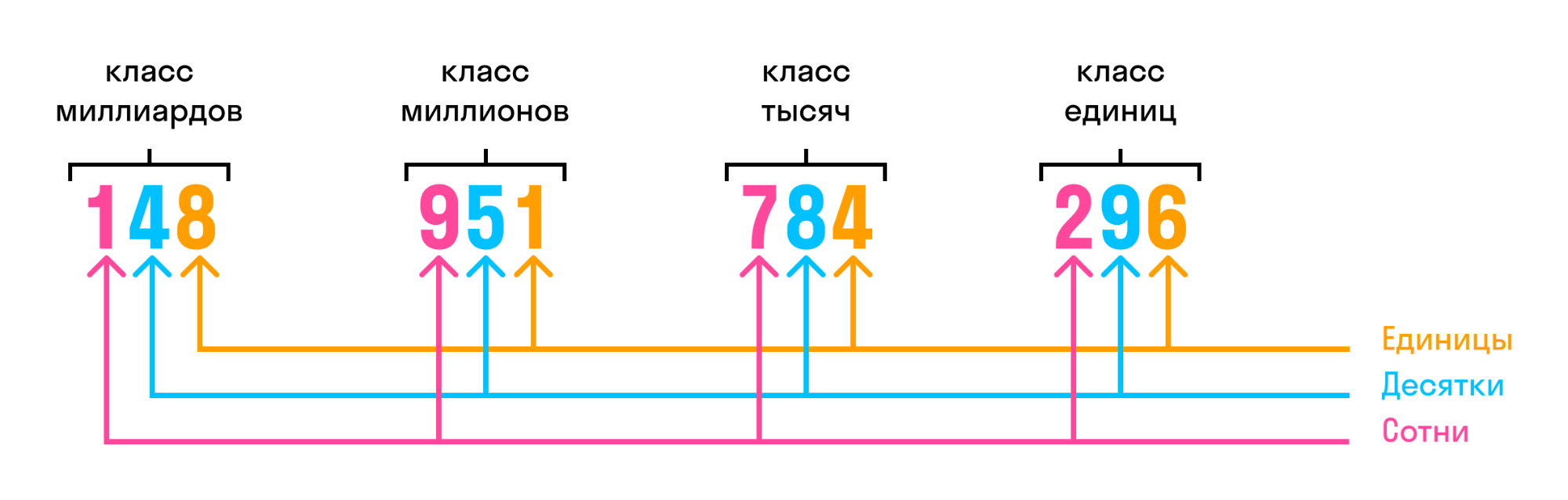
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.
Названия классов многозначных чисел:
первый — класс единиц,
второй — класс тысяч,
третий — класс миллионов,
четвёртый — класс миллиардов,
пятый — класс триллионов,
шестой — класс квадриллионов,
седьмой — класс квинтиллионов,
восьмой — класс секстиллионов.
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
345 466 129 350 вместо 345466129350
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.
Разрядные единицы — это единицы, десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы и т. д.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
10 единиц = 1 десяток;
10 десятков = 1 сотня;
10 сотен = 1 тысяча;
10 тысяч = 1 десяток тысяч;
10 десятков тысяч = 1 сотня тысяч;
10 сотен тысяч = 1 миллион.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
Например, нужно сказать, сколько сотен в числе 5689.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. Мысленно вычеркиваем разряды правее сотен, остается две цифры: 56. Значит, в числе 5689 56 сотен.
Если в разряде стоит цифра 0 — это означает отсутствие единиц данного разряда.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
Разберем число 6 057 386
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
шести единиц миллионов (6 * 1 000 000);
пяти десятков тысяч (5 * 10 000);
семи единиц тысяч (7 * 1000);
трех сотен (3 * 100);
восьми десятков (8 * 10);
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц каждого разряда в числе 5 068 252.
1. Определяем сколько всего единиц в числе.
2. Определяем количество десятков.
Записываем число без первого разряда (единицы).
3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).
4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).
5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).
6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.
7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.
Расписав таким образом число, мы выяснили, что в числе 5 068 252 содержится 5 миллионов, 50 сотен тысяч, 506 десятков, 5068 тысяч, 50 682 сотни, 506 825 десятка, 5 068 252 единицы.
А если разобрать число по классам, то можно сказать, что число 5 068 252 содержит 5 единиц класса миллионов (третий класс), 68 единиц класса тысяч (второй класс), 252 единицы класса единиц (первый класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
84 610 = 8 × 10 000 + 4 × 1 000 + 6 × 100 + 1 × 10
84 610 = 80 000 + 4 000 + 600 + 10.
45 317 = 4 × 10 000 + 5 × 1000 + 3 × 100 + 1 × 10 + 7 × 1
45 317 = 40 000 + 5 000 + 300 + 10 + 7.
56 789 = 5 × 10 000 + 6 × 1000 + 7 × 100 + 8 × 10 + 9 × 1
56 789 = 50 000 + 6 000 + 700 + 80 + 9.
345 677 = 3 × 100 000 + 4 × 10 000 + 5 × 1000 + 6 × 100 + 7 × 10 + 7 × 1
345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
687 543 = 6 × 100 000 + 8 × 10 000 + 7 × 1000 + 5 × 100 + 4 × 10 + 3 × 1
687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
877 589 = 8 × 100 000 + 7 × 10 000 + 7 × 1000 + 5 × 10 + 8 × 10 + 9 × 1
877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
4 895 634 = 4 × 1 000 000 + 8 × 100 000 + 9 × 10 000 + 5 × 1000 + 6 × 100 + 3 × 10 + 4 × 1
4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 + 4.
8 675 349 = 8 × 1 000 000 + 6 × 100 000 + 7 × 10 000 + 5 × 1000 + 3 × 100 + 4 × 10 + 9 × 1
8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
77 897 125 = 7 × 10 000 000 + 7 × 1 000 000 + 8 × 100 000 + 9 × 10 000 + 7 × 1000 + 1 × 100 + 2 × 10 + 5 × 1
77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
656 734 212 = 6 × 100 000 000 + 5 × 10 000 000 + 6 × 1 000 000 + 7 × 100 000 + 3 × 10 000 + 4 × 1000 + 2 × 100 + 1 × 10 + 2 × 1
656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
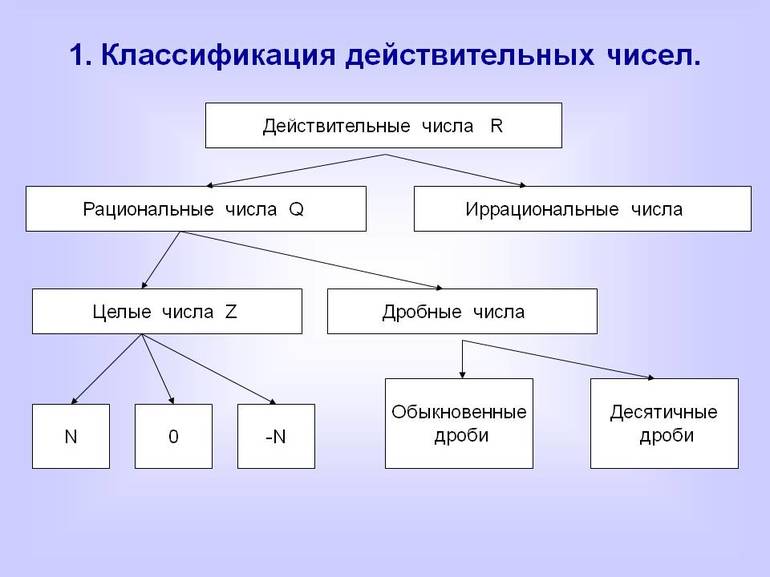
Натуральные числа и их классификация
Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.
Главной особенностью этого ряда считается его бесконечность. Она обусловлена тем, что самого большого числа не существует. У любой составляющей ряда есть «старшие товарищи» — величины, которые по своему значению больше.
Распределение по категориям
Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):
Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:
Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).
Разрядные составляющие — это натуральные числа, содержащие только одну цифру, отличную от нуля. Примеры разрядных слагаемых: 7, 30, 200, 4000 и тому подобные. Числа такого вида, как 12, 21, 475, 3500 и так далее, не могут быть отнесены к этой категории. Они подлежат математическому разложению на составляющие.
Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.
Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.
Комплектация разрядов
В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.
Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:
Распределение по классовым и разрядным категориям отображено в таблице:
Особенности разложения
Чтобы лучше понять, что такое разрядные слагаемые в математике и как их использовать, стоит подробно рассмотреть процесс разложения натуральных величин на эти составляющие. В основе большинства задач с разрядными слагаемыми лежит разложение натурального числа, то есть его представление в виде суммы разрядов через сложение количеств всех разрядных единиц.
Преобразить в сумму разрядных слагаемых можно каждую натуральную величину составного типа, то есть многозначную (двузначную, трехзначную и так далее). Чтобы разложить число на разрядные слагаемые корректно, необходимо соблюдать основные правила. Первое — нули не учитываются в разрядном составе числа. Второе — слагаемые записываются в порядке старшинства, то есть от старшего к младшему — вначале тысячи, затем сотни и десятки, последними фиксируются простые единицы.
Разрядный состав можно записать в трех вариантах разбора:
Вне зависимости от выбранного способа разложить число на составляющие по разрядам не составит особого труда. Конечно, чем больше число, тем выше риск запутаться и совершить ошибку. Упражняться лучше сперва на двузначных числах, а затем постепенно повышать разрядность.
Упражнения для тренировки
Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:
Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:
Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.
Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений. Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.
Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.
Урок 11 Бесплатно Разложение числа по разрядам. Способы сложение натуральных чисел
Вы уже имеете общее представление об арифметической операции сложения и знаете свойства сложения натуральных чисел.
Сегодня вспомним наименования разрядов и классов.
Выясним, как записывают и читают большие натуральные числа.
Разберемся, что представляют собой разрядные слагаемые и как определить сумму разрядных слагаемых.
Познакомимся с различными способами и приемами сложения многозначных натуральных чисел, закрепим полученные знания на примерах.
Разряды и классы
С давних времен люди стремились не только уметь считать, но и уметь записывать числа.
Сначала для записи чисел применяли черточки, точки, метки и другие способы представления количества чего-либо, сейчас для этих целей используют цифры.
Сегодня цифры и числа окружают нас повсюду.
Мы не можем себе представить дату без чисел, невозможно измерить рост, массу, время, возраст, считать предметы, совершить покупку, продать, позвонить и т.д.
Число- это математическое понятие, которое используется для количественной характеристики, нумерации объектов и их частей, сравнения.
Каждое число состоит из цифр.
Цифрой называют знак, используемый для записи числа.
Цифры, которые мы используем в повседневной жизни, называют арабскими.
Их существует всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Все цифры кроме нуля называют значащими.
Нуль- это знак, который не указывает никакого числа, т.е. указывает на его отсутствие.
Запись числа с помощью десяти арабских цифр называют десятичной системой счисления.
Название системы счисления определяется ее основанием: количеством цифр, которые используются в данной системе счисления.
Цифры, из которых строятся числа десятичной системы счисления, называют узловыми:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Все остальные числа, которые состоят из узловых, называют алгоритмическими, например, 48, 35, 675, 2468 и т.д.
Десятичная система счисления является позиционной системой счисления, так как значение каждой цифры, из которых состоит число, зависит от ее позиции (места) в этом числе.
Место записи цифры в числе называют разрядом числа.
Счет разрядов идет справа налево.
В записи числа первая цифра справа называется цифрой первого разряда (разряд единиц)- это самый младший разряд.
Например, в числе 182 три разряда: первый разряд (разряд единиц) состоит из 2 единиц, второй разряд (разряд десятков) состоит из 8 десятков, третий разряд (разряд сотен) состоит из 1 сотни.
Если в записи числа вместо какого-либо разряда стоит «0» (нуль), то это означает, что цифра данного разряда отсутствует.
Сравним прочтение чисел 201 и 241
Каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Например, единицы называют простыми единицами.
10 простых единиц составляют десяток.
10 десятков составляют сотню.
10 сотен составляют тысячу.
10 тысяч (один десяток тысяч) составляют десять тысяч (10000)
10 десятков тысяч составляют сто тысяч (100000)
Числа, которые записаны с помощью одной цифры, называют однозначными числами (числами первого порядка).
Числа, записанные с помощью двух цифр, называют двузначными числами (числами второго порядка).
Числа, которые состоят из трех цифр, называют трехзначными (числами третьего порядка) и т.д.
Пример:
1, 2, 5, 6— однозначные числа.
Самое маленькое однозначное натуральное число 1, самое большое- 9
10, 24, 38, 85— двузначные числа.
Самое маленькое двузначное натуральное число 10, самое большое- 99
278, 456, 882, 312— трехзначные числа.
Самое маленькое трехзначное натуральное число 100, самое большое- 999
Числа, для записи которых используют более одной цифры, называют многозначными числами.
Для удобства чтения многозначных чисел их разбивают на группы по три цифры, начиная справа; такие группы цифр называют классами.
Каждый класс содержит три разряда, записанных справа налево, начиная с разряда единиц, далее разряд десятков, затем идет разряд сотен.
Самый последний левый класс натурального многозначного числа может состоять из одного или двух разрядов.
Каждый класс имеет свое название.
Разряды повторяются по очереди в каждом классе, обозначая единицы, десятки и сотни соответствующих классов тысяч, миллионов, миллиардов и т.д.
Изобразим таблицу классов и разрядов натуральных чисел.
Таблица классов и разрядов чисел
У меня есть дополнительная информация к этой части урока!
Числа, которые имеют более 12 разрядов, т.е. числа от пятого класса и выше относятся к большим числам.
Числа, идущие после миллиарда названы в соответствии с латинскими наименованиями числительных.
Каждый последующий класс больших чисел содержит 1000 предыдущих.
1000 миллиардов = 1 триллион (представляет собой единицу и 12 нулей).
«Три» по латыни означает число «три».
1000 триллионов = 1 квадриллион (представляет собой единицу и 15 нулей)
«Квадра» по латыни означает число «четыре».
1000 квадриллионов = 1 квинтиллион (представляет собой единицу и 18 нулей)
«Квинта» по латыни- «пять» и т.д.
«Числа-гиганты» в повседневной жизни используют редко.
Применяются в основном в физике и астрономии для измерения массы и размеров звезд и планет, для расчета расстояний до различных небесных тел, расстояний между ними и т.д.
Удивительно, но большие числа можно отметить в человеческом теле.
Так, например, человеческий мозг состоит из 100 миллиардов нервных клеток- нейронов.
Посмотрим, как правильно читается большое число.
Чтобы прочитать многозначное натуральное число 184567483265, разобьем его на классы: Получим число вида: 184 567 483 265.
Прочитаем число, называя по очереди число единиц каждого класса слева направо.
При чтении класса единиц название данного класса, которым заканчивается любое натуральное число, не произносится.
184 миллиарда 567 миллионов 483 тысячи 265.
Не произносится также название класса, все три цифры которого нули.
Например, число 149500000 километров (число равное расстоянию от Земли до Солнца) прочитаем так: 149 миллионов 500 тысяч километров.
Пройти тест и получить оценку можно после входа или регистрации
Способы сложения натуральных чисел
Вы уже имеете общее представление об операции сложения чисел и знаете свойства сложения натуральных чисел.
Уроком ранее мы выяснили, что сложение- это арифметическая операция объединения исчисляемых объектов в одно целое.
Результат сложения чисел называют суммой этих чисел.
Складываемые числа называют слагаемыми.
Для записи сложения используют знак плюс «+»
В повседневной жизни, на работе, на учебе возникает необходимость оперативно и качественно решать задачи и производить определенные арифметические действия, выбирая для этого оптимально удобный способ решения.
Сейчас рассмотрим некоторые способы и приемы, позволяющие верно, быстро и легко вычислит сумму натуральных чисел.
1. Таблица сложения натуральных чисел
Для сложения чисел первого десятка удобно пользоваться таблицей сложения, с которой вы знакомились в начальных классах.
Запомнив данную таблицу наизусть, легко и просто выполнить задание на вычисление суммы чисел.
Разберем правила пользования таблицей сложения натуральных чисел.
Известно, что операция сложения выглядит так:
Слагаемое №1 + Слагаемое №2 = Сумма
Таблица представляет собой квадрат, разбитый на десять строк и десять столбцов.
По верхнему краю и по левому краю пронумерованы ячейки от 1 до 10
У меня есть дополнительная информация к этой части урока!
Алгоритм сложения двух натуральных чисел с помощью таблицы:
1. В самой верхней строке необходимо выбрать из десяти ячеек ту, в которой содержится значение первого слагаемого.
2. Выбрать в самом левом столбце ячейку, в которой находится значение второго слагаемого.
3. Суммой будет являться число, расположенное в ячейке, образованной пересечением соответствующих столбца и строки в поле таблицы.
Например, чтобы сложить два натуральных числа 4 и 7, нужно выполнить следующие действия:
Таким образом, 4 + 7 = 11
Такой же результат будет получен, если с помощью таблицы сложим 7 и 4.
Таким образом, 7 + 4 = 11
Таблицей удобно пользоваться при сложении многозначных чисел по разрядам, если условно принять, что в таблице складываются десятки с десятками или сотни с сотнями, или тысячи с тысячами и т.д.
Пример:
Найдите сумму чисел 20 и 60 с помощью таблицы сложения натуральных чисел.
С помощью таблицы уже известным способом сложим числа 2 и 6, суммой данных чисел является ячейка со значением 8.
Условно представим, что ячейка со значением 2— это 2 десятка, ячейка со значением 6— это 6 десятков.
Следовательно, ячейка с результатом 8, образованная пересечением соответствующего столбца и строки, по смыслу означает 8 десятков.
20 + 60 = 80
Ответ: 80
Для перехода при сложении на следующий разряд вспомним, что каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Пример:
Вычислите по таблице сумму чисел 700 и 300.
С помощью таблицы уже известным способом сложим числа 7 и 3, суммой данных чисел является ячейка со значением 10
Условно представим, что ячейка со значением 7— это 7 сотен, ячейка со значением 3 означает 3 сотни.
Следовательно, ячейка с результатом 10, образованная пересечением соответствующего столбца и строки, по смыслу означает 10 сотен.
Нам известно, что 10 сотен = 1000
Таким образом, получаем 700 + 300 = 1000
Ответ: 1000
Пример:
Вычислите сумму 60 и 70 с помощью таблицы сложения.
По таблице сложения чисел видно, что 6 + 7 = 13
Следовательно, если сложить 6 десятков и 7 десятков, получим 13 десятков.
Так как число 13 состоит из 1 десятка и 3 единиц, то 13 десятков состоят из 10 десятков и 3 десятков.
10 десятков = 100
3 десятка = 30
Получим 100 + 30 = 130.
Ответ: 130
Конечно, таблица сложения натуральных чисел позволяет наглядно легко и быстро определить сумму чисел, но не всегда она находится под рукой.
2. Способ поразрядного сложения натуральных чисел.
Рассмотрим еще один способ определения суммы чисел.
Первым делом научимся представлять натуральные числа в виде суммы разрядных слагаемых.
Разрядные слагаемые натурального числа имеют ряд характерных признаков:
1. Разрядные слагаемые- это числа, в записи которых находится только одна цифра, отличная от нуля.
Например, 10, 200, 6000, 40000 и т.д.
2. Разрядные слагаемые одного натурального числа имеют разное количество знаков в своей записи (т.е. состоят из разного количества цифр).
3. Количество разрядных слагаемых натурального числа должно быть равно количеству цифр, отличных от нуля, в записи числа.
Сумма разрядных слагаемых— это запись многозначного числа, как суммы его разрядных единиц.
Сумма разрядных слагаемых равна исходному натуральному числу.
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Для этого необходимо:
1. Определить по количеству цифр в числе количество разрядных слагаемых, отличных от нуля.
2. Определить количество единиц, десятков, сотен, тысяч и т.д.
3. Записать число в виде суммы разрядных слагаемых.
Пример:
Разложите натуральное число 2456 в виде суммы разрядных слагаемых.
Число 2456 представляет собой сумму четырех разрядных слагаемых (так как число состоит из 4 цифр, неравных нулю).
Число 2456 содержит:
2456 = 2 тысячи + 4 сотни + 5 десятков + 6 единиц = 2000 + 400 + 50 + 6
Рассмотрим алгоритм поразрядного сложения натуральных чисел.
1. Слагаемые разложить на разрядные слагаемые.
2. Выполнить сложение одноименных разрядов (единиц с единицами, десятки с десятками и т.д.) используя при этом переместительное и сочетательное свойства сложения.
Пример:
Найдите сумму чисел 245 и 25 способом последовательного поразрядного сложения.
Разложим первое и второе слагаемое на разрядные слагаемые.
245 = 2 сотни + 4 десятка + 5 единиц = 200 + 40 + 5
25 = 2 десятка + 5 единиц = 20 + 5
Выполним сложение одноименных разрядов чисел 245 и 25.
245 + 25 = 200 + 40 + 5 + 20 + 5 = 200 + (40 + 20) + (5 + 5) = 200 + (60 + 10) = 200 + 70 = 270
Получаем 245 + 25 = 270
Ответ: 270
3. Сложение натуральных чисел «столбиком»
Рассмотренный способ поразрядного сложения довольно громоздкий в оформлении и не очень удобный для определения суммы больших чисел или нескольких больших чисел.
Поэтому часто многозначные числа складывают в столбик.
Чтобы сложить натуральные числа данным способом, нужно записать слагаемые в столбик так, чтобы цифры одноименных разрядов находились друг под другом (единицы под единицами, десятки под десятками, сотни под сотнями и т.д.).
При сложении столбиком самая правая цифра одного числа (разряд единиц первого слагаемого) должна располагаться под самой правой цифрой другого числа (разряд единиц второго слагаемого).
Нам известно, что от перестановки слагаемых сумма не меняется, следовательно, записывать слагаемые в столбик можно в любом порядке.
Затем слева между числами-слагаемыми ставится знак плюс «+».
Под нижним слагаемым проводится горизонтальная черта.
Сложение чисел начинается с разряда единиц (с крайнего правого столбца).
Складывают цифры одного разряда, результат записывают под горизонтальной чертой под тем разрядом, в котором выполнялось сложение.
Если в результате получается число меньше 10 (однозначное число), то оно записывается в столбик соответствующего разряда под чертой.
Если в результате получается двузначное число, то под чертой записывается значение разряда единиц полученного числа, а число десятков либо запоминается (держится в уме), либо подписывается сверху над следующим столбиком в дополнительной строке.
Далее складываются числа в следующем столбике, т.е. складываются значение следующего разряда слагаемых.
Действия совершаются аналогично изложенным выше, однако к суме еще добавляется число десятков, которые «держали в уме» (если такое было).
Соответственно, если получается однозначное число, его записывают под чертой в столбик соответствующего разряда.
Если число в результате сложения получается двузначное, то снова под линией записывается число единиц полученного промежуточного значения, а значение десятков запоминается или записывается в дополнительной строке.
Так происходит переход к следующему столбику (следующим разрядам слагаемых) и производятся все выше описанные действия.
Натуральное число, которое образуется после завершения операции сложения, является результатом суммы исходных чисел.
Пример:
Выполните сложение двух чисел 75806 и 2798.
Запишем два числа в столбик так, чтобы одноименные разряды стояли друг под другом.
Между числами поставим знак плюс «+», под нижним слагаемым проведем горизонтальную черту.
Складываем числа из правого столбца: 6 и 8.
Получаем число 14— двузначное число.
Под горизонтальной линией записываем число 4 (значение разряда единиц числа 14), а число 1 (значение разряда десятков числа 14) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Продолжаем вычисление, складываем цифры слагаемых, стоящих во втором столбце справа.
Так как 0 + 0 = 0, но была запомнена 1, то получим 0 + 0 + 1 = 1
Число 1— однозначное число, следовательно, его просто записываем под чертой в соответствующем разряде.
Переходим к следующему столбцу.
Складываем 8 и 9, при этом в памяти нет никаких запомненных чисел, поэтому больше ничего к ним не прибавляем
8 + 9 = 17
Получили двузначное число 17.
Следовательно, число 7 записываем под горизонтальной чертой (значение разряда единиц числа 17), а число 1 (значение разряда десятков числа 17) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Переходим к четвертому столбцу.
Складываем 5 и 7.
В памяти была запомнена 1, поэтому к сумме чисел 5 и 7 прибавляем 1.
5 + 7 + 1 = 13
Получили двузначное число 13.
Следовательно, число 3 записываем под горизонтальной чертой, а число 1 запоминаем, переносим в следующий разряд.
На последнем шаге складываем 2 и 7
2 + 7 = 9
К 9 прибавляем запомненную 1, получаем: 9 + 1 = 10
Но в следующем столбце исходные слагаемые не имеют цифр, запомненную 1 сносим вниз и записываем под чертой.
Сложение двух натуральных чисел 75806 и 27908 завершено, сумма данных чисел равна 103714
75806 + 27908 = 103714
Ответ: 103714
Столбиком можно складывать различное количество слагаемых.
Алгоритм выполнения операции сложения в столбик нескольких слагаемых будет абсолютно аналогичным.
4. Группировка слагаемых и округление натуральных чисел.
Данный способ сложения натуральных чисел кратко уже был рассмотрен на прошлом уроке.
Известно, что число, которое оканчивается на нуль или несколько нулей, называют круглым числом.
С круглыми числами легко совершать арифметические операции.
Сложение способом округления натуральных чисел применяют, когда из слагаемых можно выбрать такие, которые в сумме будут давать круглые числа.
Разность между круглым и исходным числом называется арифметическим дополнением.
Чтобы произвести сложение многозначных натуральных чисел способом округления, необходимо:
1. Одно из слагаемых, которое близко к круглому числу, округлить.
2. Выполнить операцию сложения.
3. Из полученной суммы вычесть арифметическое дополнение.
Пример:
Найдите сумму чисел 1448 и 298
Округлим число 298 до 300, а затем вычтем из полученной суммы арифметическое дополнение, равное 2
Получим выражение вида:
Ответ: 1746
Совместно с данным способом сложения натуральных чисел используют группировку слагаемых и применяют основные свойства сложения.
При вычислении суммы, состоящей из трех и более слагаемых, удобно использовать переместительное и сочетательное свойство сложения, группируя слагаемые, объединяя их по определенному признаку с помощью скобок таким образом, чтобы в сумме они давали круглые числа.
Пример:
Найдите сумму чисел 46 + 28 + 134 + 61
Группируем числа так, чтобы в результате сложения этих чисел получалось круглое число.
Используя переместительное и сочетательное свойство сложения, переставим местами слагаемые и сгруппируем их.
46 + 28 + 134 + 61 = (46 + 134) + (28 + 61) = 180 + 89
Округлим число 89 до 90
В связи с этим из суммы чисел 180 и 90 вычтем арифметическое дополнение, равное 1
Ответ: 269
Пройти тест и получить оценку можно после входа или регистрации
Разложение числа на разрядные слагаемые
В данной публикации мы рассмотрим, что такое разрядные слагаемые, и как число представить в виде их суммы (или разложить на них). Также разберем примеры для лучшего понимания изложенного материала.
Сумма разрядных слагаемых
Любое натуральное многозначное число (в нем содержится несколько цифр) может быть записано в виде суммы разрядных слагаемых.
Число “47” состоит из четырех десятков и семи единиц.
Т.е. 47 = 4 · 10 + 7 · 1 = 40 + 7
Действие выше называется разложением на разрядные слагаемые (или их суммой), которыми в данном случае являются числа “40” и “7”.
Примеры:
Множители 1, 10, 100, 1000 и т.д. – это разрядные единицы.
Пример задачи
Разложим число на разрядные слагаемые и определим количество единиц каждого разряда.
Решение:
В заданном числе содержится:
Запишем число в виде суммы разрядных слагаемых:
Для того, чтобы определить, сколько разрядных единиц содержится в числе, мы просто переписываем его до того разряда, количество единиц которого нужно найти. В нашем случае получается:
2 класс. Математика. Разрядные слагаемые
2 класс. Математика. Разрядные слагаемые
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
§1. Понятие «разрядные слагаемые»
В этом занятии познакомимся с понятием «разрядные слагаемые» и научимся раскладывать числа на разрядные слагаемые.
Давайте решим задачу:
Красная Шапочка отправилась в гости к своей бабушке.
И взяла она с собой гостинец для бабушки – корзинку с пирожками.
У Красной Шапочки в корзинке было 10 пирожков с капустой и 7 пирожков с грибами. Сколько всего пирожков у Красной Шапочки в корзинке?
Чтобы ответить на вопрос задачи, необходимо выполнить сложение, а именно к 10 пирожкам с капустой прибавить 7 пирожков с грибами.
10 + 7 = 17 (пирожков).
Значит, 17 пирожков всего было в корзинке у Красной Шапочки.
Обратим внимание на получившееся при решении задачи числовое выражение:
Назовем все компоненты сложения.
Первое число 10 – первое слагаемое, число 7 – второе слагаемое и число 17 – сумма.
А что мы еще можем сказать про числа 10, 7 и 17?
Число 10 – это двузначное число, записанное двумя цифрами 1 и 0.
Число 10 относится к разряду десятков и равняется 1 десятку.
Число 7 – это однозначное число, записанное одной цифрой 7.
Это число относится к разряду единиц.
Заменим слагаемые 10 и 7 в нашем числовом выражении разрядными числами.
Так, первое слагаемое 10 = 1 десятку, а второе слагаемое 7 = 7 единицам.
Получили следующее числовое выражение:
1 десяток + 7 единиц = 17.
Значит, число 17 – это двузначное число, записанное двумя цифрами 1 и 7.
Оно состоит из 1 десятка и 7 единиц.
Обратим внимание на получившееся выражение: 1 десяток + 7 единиц = 17.
Назовем компоненты сложения.
Первое слагаемое – 1 десяток, второе слагаемое – 7 единиц, сумма – число 17.
И первое, и второе слагаемые представлены разрядными числами.
Значит, эти слагаемые можно назвать разрядными слагаемыми.
§2. Разложение чисел на разрядные слагаемые
Запишем числовые выражения 10 + 7 = 17 и 1 десяток + 7единиц =17 как одно числовое выражение:
1 десяток + 7 единиц = 10 + 7 = 17.
Слагаемые 10 и 7 тоже будут разрядными слагаемыми, так 10 = 1 десятку, а 7 = 7 единицам.
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Например, число 53 состоит из 5 десятков и 3 единиц.
53 = 5 десятков + 3 единицы = 50 + 3
Представление числа в виде: 53 = 50 + 3 называется разложением числа на разрядные слагаемые или суммой разрядных слагаемых.
А числа 50 и 3 называются разрядными слагаемыми.
Числа 1, 10, 100, 1000 и т.д. – называются разрядными единицами.
Так, 1 – это единица разряда единиц;
10 – единица разряда десятков;
100 – единица разряда сотен и т.д.
Например, про число 50 можно сказать, что это 5 единиц разряда десятков, а про число 3 мы скажем – это 3 единицы разряда единиц.
Чтобы разложить число на разрядные слагаемые, необходимо:
1. определить количество всех единиц какого-либо разряда, т.е. сколько в числе единиц, десятков, сотен и т.д.;
2. записать число в виде суммы разрядных слагаемых.
Представим еще одно число, число 72, в виде разрядных слагаемых:
Подчеркнем одной чертой единицы в этом числе, а двумя чертами – десятки: 72.
Запишем число 72 в виде суммы разрядных слагаемых.
§3. Краткие итоги урока
Подведем итоги урока:
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Представление числа в виде: 53 = 50 + 3 называется разложением числа на разрядные слагаемые или суммой разрядных слагаемых. А числа 50 и 3 называются разрядными слагаемыми.
Чтобы разложить число на разрядные слагаемые, необходимо:
1) определить количество всех единиц какого-либо разряда, т.е. сколько в числе единиц, десятков, сотен и т.д.;
2) записать число в виде суммы разрядных слагаемых.
Числа 1, 10, 100, 1000 и т.д. – называются разрядными единицами. Так, 1 – это единица разряда единиц; 10 – единица разряда десятков; 100 – единица разряда сотен и т.д.
ИСТОЧНИКИ
Файлы
Нет дополнительных материалов для этого занятия.
Сумма разрядных слагаемых натурального числа
Время чтения: 12 минут
Для того, чтобы выполнить некоторые действия над натуральными числами необходимо представить эти числа в виде суммы разрядных составляющих или, как говорят, разложить натуральные числа на цифры. Не менее важен и обратный процесс, который заключается в записи натурального числа в виде суммы разрядных составляющих.
Как найти натуральное число, если известна его подобная сумма?
Для того, чтобы проделывать некоторые действия, нужно представлять начальные выражения в виде сложенных чисел – другим языком, необходимо разложить числа по разрядам. Противоположный процесс также безгранично важен при решении задач и упражнений.
Разрядные слагаемые – это такие числа, которые состоят исключительно из нулей и единственной цифры, отличной от нуля. Такие натуральные числа, как 5, 20, 400, 100, принадлежат данной категории, а числа 55, 213, 680, 324, 458, 25, 694, 25 и другие – не относятся.
Число разрядных слагаемых у некоторого числа равно тому числу, сколько цифр содержатся в записи. Представление числа 61 в виде суммы разрядных слагаемых, станет выглядеть как 6 и 1, они отличаются от 0. Когда есть необходимость разложить 55050 как сумму слагаемых разрядов, оно будет представлено в виде трех слагаемых. Три пятерки, что присутствуют в записи, отличны от нуля.
Необходимо помнить, что каждое разрядное слагаемое содержит отличное от других количество знаков в собственной записи.
Сумма разрядных слагаемых числа, принадлежащего к классу натуральных, обязательно эквивалентна данному числу.
Натуральные числа, в записи которых присутствует цифра, что отлична от нуля, называются разрядными слагаемыми.
Количество чисел обязано быть равно количеству тех цифр, которые не равных нулю. Каждое слагаемое может быть записано с разным количеством знаков. Если необходимо разложить по разрядам, то при сложении получившихся цифр, мы получим число равно данному числу.
При анализе понятия, можно сформулировать вывод, что многозначные и однозначные числа, которые полностью состоят из нулей за исключением первой цифры, нельзя представлять в виде суммы. Это происходит в том случае, когда такие числа сами будут разрядными слагаемыми для каких-то чисел.
Исключая данные числа, все остальные примеры могут раскладываться на слагаемые.
Правила разложения чисел
Чтобы разложить число на сумму разрядных слагаемых, необходимо вспомнить, что каждое натуральное число связано с количеством определенных элементов. При записи числа разложение зависит от числа единиц, десятков, сотен, тысяч и т.д. К примеру, если взять число 937, то можно увидеть, что ему соответствует 9 сотен, 3 десятка и 7 единиц. Число 245 500 соответствует 2 сотням тысяч, 4 десяткам тысяч, 5 тысячам и 5 сотням. Эти числа можно представить в виде равенств — 900 + 30 + 8 = 938 и 245 500 = 200 000 + 40 000 + 5 000 + 500. В данных примерах можно наглядно увидеть, как число можно разделить на сумму цифр. Рассматривая этот пример, мы можем представить всевозможное натуральное число в виде суммы его разрядных членов. Вот еще один пример. Представим натуральное число 724 как сумму составляющих цифр. 724 равно 7 сотням, 2 десяткам и 4 единицам, поэтому 724 = 700 + 20 + 4. Однако сумма 312 + 412 не является суммой составляющих цифр числа 724, потому что нельзя иметь два числа, которые состоят из одинакового количества цифр. Мы уже рассматривали ключевое понятие. Разрядные слагаемые названы так потому, что они принадлежат к конкретному разряду.
Нет времени решать самому?
Наши эксперты помогут!
Примеры задач
Пример 1. Известна сумма разрядов, как же найти само число?
Чтобы решить этот пример, давайте рассмотрим обратную задачу. Представим, что мы знаем сумму слагаемых цифр. Нам нужно найти заданное натуральное число.
Например, сумма 300 + 40 + 9 равна 349, а сумма 30 000 + 3 000 + 600 + 20 + 7 соответствует натуральному числу 33627. Поэтому легко определить натуральное, если вы знаете сумму его вспомогательных слагаемых.
Другой способ найти натуральное — сложить столбцы сумм цифр. Этот пример не должен вызвать у вас затруднений. Рассмотрим его более подробно.
Пример 2. Нужно найти исходное число, когда дана сумма разрядных концов 300 000 + 50 000 + 2000+ 400 + 40 + 7.
Далее приступим к решению. Необходимо записать числа 300 000, 50 000, 2000, 400, 40, 7 сложить в столбик: осталось лишь сложить все числа в столбик. Важно помнить о том, что сумма нулей равна нулю и что сумма нулей и натурального числа равна натуральному числу.
Таким образом, выполнив сумму, мы получаем натуральное — 352447, сумма цифр которого равна 300 000 + 50 000 + 2000 + 400 + 40 + 7.
Поговорим еще об одном методе. Если мы научились делить числа и преобразовывать их в виде суммы понятий с цифрами, мы также можем представлять данные числа в виде некоторой суммы без цифр.
Пример 3. Разложение числа 5825 представляется как 49565 = 40000 + 9000 + 500 + 60 + 5, а сумма разрядных компонентов 5000 + 800 + 20 + 5 может быть представлена как (40000 + 9000) + (500 + 60) + 5 = 49565 или (40000 + 9000 + 500 + 60) + 5 = 49565 или 40000 + (9000 + 500 + 60) + 5 = 49565 и многие другие способы. Иногда сложные расчеты можно немного упростить. Приведем еще один небольшой пример для наилучшего закрепления представленной информации.
Пример 4. Вычтите числа 67838 и 780. Сначала представим — 67838 как сумму разрядных компонентов: 67838 = 60000 + 7000 + 800 + 30 + 8. Выполнив операцию, можно сделать вывод, что сумма (60000+7000)+ (800 + 30 + 8) = 67000 + 838. Тогда 67838 — 780 = (67000 + 838) — 780 = 67000 + (838 — 780) = 67000 + 58 = 67058.
Стоит рассмотреть обратную задачу более подробно. Считайте, что у нас есть сумма разрядных составляющих натурального числа, и нам нужно найти это число.
Например, сумма 300+20+9 является разложением разрядных чисел 329, а сумма разрядных слагаемых вида 3 000 000 + 40 000 + 4 000 + 500 соответствует натуральному числу 3 044 500.
То есть 600 + 20 + 9 = 629, а 3 000 000 + 30 000 + 4 000 + 500 = 3 034 500.
Чтобы найти положительное число по известной сумме разрядных слагаемых, можно сложить эти разрядные слагаемые в столбик (при необходимости обратитесь к материалу по сложению целых положительных чисел в столбик). Рассмотрим решение этого примера.
Найдите целое положительное, если сумма разрядных составляющих равна 200 000 + 40 000 + 50 + 5.
Запишите числа 200 000, 40 000, 50 и 5 так, как того требует метод сложения в столбик:
Осталось только сложить все эти числа в столбик:
Под горизонтальной чертой мы получили искомое натуральное число.
В заключение мы хотели бы обратить ваше внимание еще на один момент. Умение раскладывать натуральные числа на цифры и умение выполнять обратное действие позволяет представить натуральное в виде суммы слагаемых, которые не являются разрядными.
Например, разрядное сложение целых положительных чисел 643 имеет следующий вид 643 = 600 + 40 + 3, а сумма разрядных слагаемых 700 + 20 + 5 в силу свойств сложения целых положительных чисел может быть представлена как (600 + 40) + 5 = 640 + 3 или 600+(40 + 3) = 600 + 43, или (600 + 3) + 40 = 603 + 40.
Возникает логичный вопрос: «Для чего это нужно? Ответ на него прост: в некоторых случаях это может упростить вычисления.
Пример 4. Вычтем целые положительные числа 5 799 и 790.
Сначала представим вычитаемое как сумму разрядных компонентов: 5 799 = 5 000 + 700 + 90 + 9.
Легко увидеть, что сумма разрядных компонентов равна сумме (5000 + 9) + (700 + 90) = 5009 + 790.
Тогда 5 799 — 790 = (5 009 + 790) — 790 = 5 009 + (790 — 790) =5 009 + 0=5 009.
Что такое разрядные слагаемые?
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Сумма разрядных слагаемых натурального числа, в виде суммы разрядных слагаемых
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах. Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5, 10, 400, 200относятся к данной категории, а числа 144, 321, 5 540, 16 441 – не относятся.
Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля. Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу. Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы.
Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее.
Если вы возьмем, например, число 58, то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4тысячам и 4 сотням.
Можно представить эти числа в виде равенств – 50+8=58 и 134 400=100 000+30 000+4 000+400. В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых. Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25=20+5. А вот сумма 17+8 не является суммой разрядных слагаемых числа 25, так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Например, сумма 200+30+8 разложено по разрядам числа 238, а сумма 3 000 000+20 000+2 000+500 соответствует натуральному числу 3 022 500. Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Пример 1
Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000+40 000+50+5. Перейдем к решению. Необходимо записать числа 200 000, 40 000, 50 и 5 для сложения в столбик:
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Выполнив сложение, мы получим натуральное число 240 055, сумма разрядных слагаемых которого имеет вид 200 000+40 000+50+5. Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Пример 2
Разложение по разрядам числа 725 будет представлено как 725=700+20+5, а сумму разрядных слагаемых 700+20+5 можно представить как (700+20)+5=720+5 или 700+(20+5)=700+25, или (700+5)+20=705+20. Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Пример 3
Выполним вычитание чисел 5 677 и 670. Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677=5 000+600+70+7. Выполнив действие, мы можем сделать вывод, что. сумме (5 000+7)+(600+70)=5 007+670. Тогда 5 677−670=(5 007+670)−670=5 007+(670−670)=5 007+0=5 007.
Что такое разрядные слагаемые
Разрядные слагаемые – это сумма чисел с разной разрядностью. Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.
Числа 1, 10, 100, 1000 и так далее – это разрядные единицы. Запишем разделение разрядных слагаемых:
Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы. Примеры разрядных слагаемых:
Рассмотрим пример определения разрядных слагаемых числа 92586
Сначала, разложим число 92586 на разрядные слагаемые и получим:
Запишем, из чего состоит число 92 586:
Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.
Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.
Примеры разложения чисел на разрядные слагаемые:123 = 100 + 20 + 3, где 100 — сотни, 20 — десятки, а 3 — единицы.Более сложный пример с большим числом разрядов:16 458 = 10 000 + 6 000 + 400 + 50 + 8, здесь 10 000 — десятки тысяч, 6 000 — тысячи, 400 — сотни, 50 — десятки, 8 — единицы.
Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:

Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Примеры на задачи.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6
Разрядные слагаемые в математике

[block >
Натуральные числа

Разряды и классы чисел
Разряды
Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.
Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.
Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.
Классы

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.
Сорок пять состоит из четырёх десятков и пяти простых единиц.
[block > Второй — тысяч, от 4 до 6 знаков:

Здесь отсутствуют слагаемые выше четвёртого разряда.

Это число содержит девять разрядных слагаемых:
В этом числе нет слагаемых выше 7 разряда.
[block > Четвёртый — миллиардов, от 10 до 12 цифр:
Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.
Разрядные слагаемые 4 класса читаются слева направо:
Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
[block > При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:
Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.
Пятый — триллионов, от 13 до 15 знаков.
Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.
Шестой — квадриллионов, 16—18 цифр.
Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.
Седьмой — квинтиллионов, 19—21 знак.
Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.
Восьмой — секстиллионов, 22—24 цифры.
Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.
Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.
Число по разрядам онлайн
Калькулятор раскладывает натуральное число на разрядные слагаемые. Возможно раскладывать числа до 18 знаков.
Как разложить натуральное число по разрядам
Разрядные слагаемые записываются от большего к меньшему. Нули не учитываются. Двигаясь слева направо берём поочерёдно по одной цифре. Оставшиеся цифры заменяем на нули. Сумма разрядных слагаемых числа равна этому числу.
Разберём пример. Разложим число 41200 на разряды. Двигаясь слева направо по числу.
Берём первую цифру 4 после неё идёт ещё 4 цифры. Меняем их на нули и записываем 40000(четыре десятка тысяч).
Берём вторую цифру 1 после неё идёт ещё 3 цифры. Меняем их на нули и записываем 3000(три единицы тысяч).
Берём третью цифру 2 после неё идёт ещё 2 цифры. Меняем их на нули и записываем 200(две сотни).
Дальше идут нули их мы не учитываем.
41200 = 40000 + 1000 + 200
Разрядное слагаемое это натуральное число, которое начинается с цифры отличной от нуля. Остальные цифры нули.
К примеру цифры 10, 20, 300, 500, 2000 и.т.д. являются разрядными слагаемыми
Разложить число на разрядные слагаемые можно несколькими способами.
Классы чисел
Разряды чисел
Математика. 3 класс
Конспект урока
Математика, 3 класс.
Урок № 53. Замена числа суммой разрядных слагаемых.
Сложение (вычитание) трёхзначных чисел
Перечень вопросов, рассматриваемых в теме:
— Как заменить трёхзначное число суммой разрядных слагаемых?
— Как упорядочивать заданные числа?
Глоссарий по теме:
ЧИСЛА – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Позиция (место) цифры в записи числа называется РАЗРЯДОМ.
Каждые три разряда натуральных чисел образуют КЛАСС.
Основная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. с. 48-49.
2. Волкова С. И. Математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018. с. 62-71.
3. Волкова С. И. Математика. Тесты. 3 кл. — М.: Просвещение, 2018. с. 38-45.
Теоретический материал для самостоятельного изучения
Как вы думаете, какова связь между этими изображениями?
Каждый ребёнок с раннего возраста умеет разбирать и собирать матрёшку. А как же этот фокус (секрет) применить к многозначным числам?
Если вы будете внимательным, то к концу урока вы научитесь раскладывать и складывать многозначные числа так же легко как матрёшку.
Вспомним, как образуются трёхзначные числа.
На первом месте стоят сотни, на втором – десятки и на третьем – единицы.
Единицы, десятки и сотни это разряды первого класса – класса единиц.
Попробуйте прочитать числа из таблицы.
Помните: читаем слева направо.
Четыреста пятьдесят шесть, шестьсот, пятьдесят, четыре.
А теперь вспомним матрёшку.
Представьте себе, что большая матрёшка это самый большой разряд. У нас это – сотни, мы не увидим следующую, пока не откроем большую и так далее. Теперь легко запомнить, что при записи разрядов на первом месте самый большой разряд.
Но может случиться так, что большой матрёшки не будет, сотен нет.
Мы же её не видим, значит и на месте этого разряда в записи числа ничего не будет.
Так было с числом 50 из таблицы.
Ноль впереди не пишется!
Как же представить многозначное число в виде суммы разрядных слагаемых?
Расставить матрёшек по порядку! (по росту)
Посмотрим, как это работает с числами.
Число шестьсот тридцать один. Все три матрёшки (разряда) на месте.
6 – сотни, 3 – десятки, 1 – единицы. Значит, в сумме разрядных слагаемых будут представлены все три разряда.
Итак, шестьсот тридцать один это сумма чисел шестьсот, тридцать и один
Каждое разрядное слагаемое показывает количество единиц в этом разряде
6 сотен – 600, 1 сотня – 100, 5 сотен – 500.
8 десятков – 80, 1 десяток – 10.
Единицы не меняются.
Итак, чтобы правильно записать число в виде суммы разрядных слагаемых, надо хорошо знать разряды.
Рассмотрим несколько примеров.
222 = 200 + 20 + 2
В числе 309 на месте десятков – 0 (нет одной матрёшки) поэтому в сумме разрядных слагаемых мы этот разряд пропускаем. Получается 309 это 300 и 9.
В числе 970 отсутствуют единицы в разряде единиц (нет последней матрёшки). Значит, в сумме этот разряд не обозначаем.
222 – все разряды на месте. Выстраиваем матрёшек по росту. 200 + 20 + 2
Это умение необходимо при сравнении, сложении и вычитании многозначных чисел.
Задания тренировочного модуля:
3. Укажите ряд чисел, расположенных в порядке убывания
Математика
Разрядные слагаемые. Диагонали прямоугольника

План урока:
Разрядные слагаемые
Начнем урок с небольшой разминки, повторим многозначные числа. Прочитайте внимательно высказывания, и если согласны с ними, то рисуйте в тетради 

Проверь себя.
Ребята, если в многозначном числе есть единицы разных разрядов, его можно заменить суммой разрядных слагаемых.
Например, при записи числа 1.536.185 используем 7 цифр, поэтому сумма будет состоять из семи слагаемых:
В виде суммы это число запишем так:
1.536.185 = 1.000.000 + 500.000 + 30.000 + 6.000 + 100 + 80 + 5
Ребята, сколько потребуется цифр для записи числа, если наивысший разряд этого числа – сотни тысяч? Воспользуемся таблицей разрядов.
По таблице видим, что для записи числа будем использовать 6 цифр.
Попробуйте самостоятельно заменить суммой разрядных слагаемых шестизначные числа 230.449 и 341.509 и понаблюдать, сколько слагаемых у вас получится.
Проверь себя.
Как вы думаете, почему получилось только 5 слагаемых?
В числе 230.449 отсутствуют единицы тысяч, на месте этого разряда стоит 0 (нуль), а в числе 341.509 отсутствуют десятки. Поэтому разрядных слагаемых получилось только 5.
А теперь попробуем «собрать» число из разрядных слагаемых. Поиграем в игру «Собери число».
Нахождение общего количества единиц какого-либо разряда в данном числе
Чтобы определить, сколько всего в числе единиц какого-то разряда, нужно хорошо знать место разряда. Давайте разберемся в этом вопросе на примере числа 2.675
Не забываем, что называть разряды нужно справа налево.
В числе 2.675 на первом месте – единицы, на втором – десятки, на третьем – сотни, а на четвертом – единицы тысяч. Определим, сколько всего единиц в этом числе. Выделим скобочкой сверху все цифры, захватывая единицы.
Свойства диагоналей прямоугольника, квадрата
Вспомним, что такое прямоугольник, и является ли квадрат прямоугольником.
Четырехугольники, у которых все углы прямые называются прямоугольниками. Среди прямоугольников можно выделить такие, у которых все стороны равны. Это квадраты.
А что такое «диагональ»?
Обозначим вершины фигур буквами.
Соединим отрезком вершины прямоугольника из верхнего угла в нижний. Место пересечения отрезков тоже обозначим буквой.
Ребята, вооружитесь ножницами! Проверим еще одно свойство прямоугольника. Вырежем из бумаги в клетку любой прямоугольник, согнем его из уголка в уголок и разрежем по линии сгиба (по диагонали). У нас получилось два треугольника. Наложите треугольники друг на друга. Сделайте вывод: равны ли треугольники?
Логические задачи
Великий ученый Михаил Васильевич Ломоносов говорил, что математику нужно любить, потому что она приводит ум в порядок. А вы, ребята, любите математику? Не пасуете перед трудными логическими задачами? Давайте попробуем разобрать несколько интересных сложных задач. Есть над чем подумать! Не спешите заглянуть в правильные ответы!
ЗАДАЧА
Учитель математики Иван Васильевич уже на пенсии. К нему в гости часто приходят школьники. Однажды ребята спросили учителя, сколько ему лет. На что Иван Васильевич хитро улыбнулся и сказал: «Будет ровно 100, если я проживу еще половину того, что уже прожил и еще один год». Подумайте и ответьте, сколько лет Ивану Васильевичу.
В решении этой задачи будем двигаться в обратную сторону от числа 100.
Сначала отнимем «еще один год».
Иван Васильевич сказал, что проживет еще половину того, что уже прожил. Значит, схематически это выглядит так:
Мы получили 3 равные части.
99 : 3 = 33(года) – составляют одну часть.
Нам нужно найти две таких части.
33 ∙ 2 = 66 (лет) – Ивану Васильевичу.
Следующую задачу попробуйте решить самостоятельно.
ЗАДАЧА
Однажды разбойники нашли под старым дубом клад в большом железном сундуке. Сундук был закрыт на замок с кодом из четырех цифр. Разбойники долго бились над расшифровкой кода, но так и не смогли открыть сундук. Ребята, попробуйте расшифровать комбинацию кодового замка и открыть сундук.
Проверь себя.
Итак, начнем подбирать цифры для кодового замка. Их четыре: обозначим точками.
Нам нужно выполнить еще два условия: набрать в сумме 17, третья цифра на 3 больше, чем первая.
3 + 1 = 4 – сумма известных цифр.
17 – 4 = 13 – сумма неизвестных цифр.
Две оставшиеся цифры должны дать в сумме 13, и обязательно третья цифра больше первой. Рассмотрим три варианта:
4 и 9 (не подходит, 9>4 на 5)
5 и 8 (подходит, 8>5 на 3)
6 и 7 (не подходит, 7>6 на 1)
Правильный ответ:
Ребята, понравились логические задачи? Они не имеют стандартного решения. Размышляйте, используйте для решения таких задач схемы, чертежи, таблицы, рисунки. У вас обязательно все получится.
До скорых встреч! А сейчас проверьте свои знания.
Памятка по математике на тему «Сумма разрядных слагаемых»
Представление числа в виде суммы разрядных слагаемых


400 – это число единиц в разряде Сотни.
20 – это число единиц в разряде Десятки.
5 – это число единиц в разряде Единицы.
Речь пока идёт о классе Единиц.
Курс профессиональной переподготовки
Руководство профильным направлением (проектом) в организации библиотечно-информационной сферы
Курс повышения квалификации
Методика работы с информационными ресурсами глобальных и национальных сетевых поисковых сервисов библиотек и информационно-библиотечных центров в условиях реализации ФГОС
Курс профессиональной переподготовки
Организация деятельности библиотекаря в профессиональном образовании
«Игра в архитектуру. «Придумай новый дизайн для старой остановки» (для учеников средней и старшей школы)»
Краткое описание документа:
Материал для учащихся четвёртых классов. Будьте внимательны!
Представление числа в виде суммы разрядных слагаемых
425 = 400 + 20 + 5
Числа 1, 10, 100, 1000 и т.д. — называются разрядными единицами. Так, 1 — это единица разряда единиц; 10 — единица разряда десятков; 100 — единица разряда сотен и т.д.
Акция до 31 августа
«Начало учебного года современного учителя»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 903 542 материала в базе
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Настоящий материал опубликован пользователем Соколова Екатерина Владиславовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
«Мотивация учебной деятельности младших школьников: психолого-педагогические аспекты»
«Хочу все знать! Как сделать исследование интересным для дошкольников»
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.