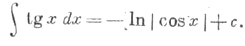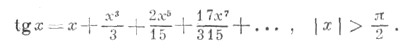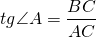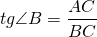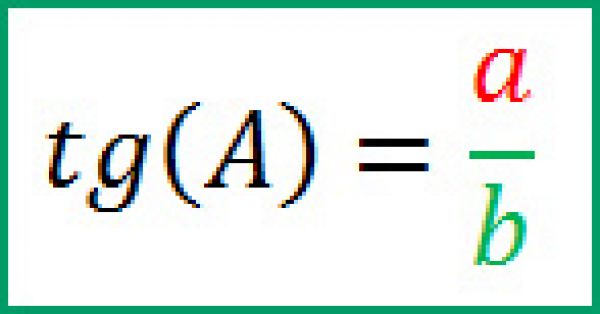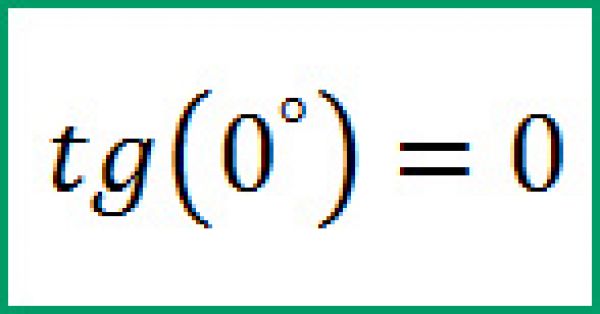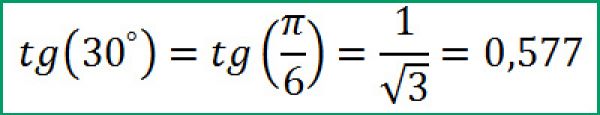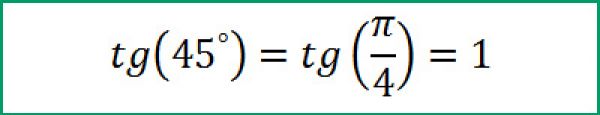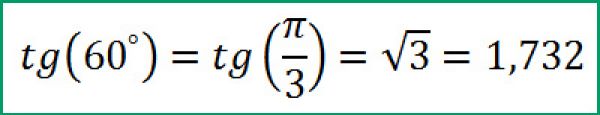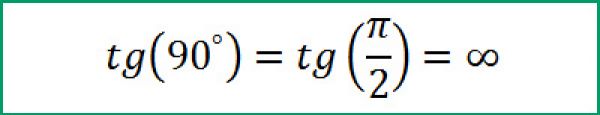Что такое тангенс угла
Что такое тангенс угла
Что такое тангенс угла. Что такое тангенс угла
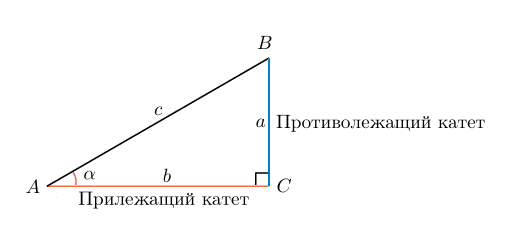
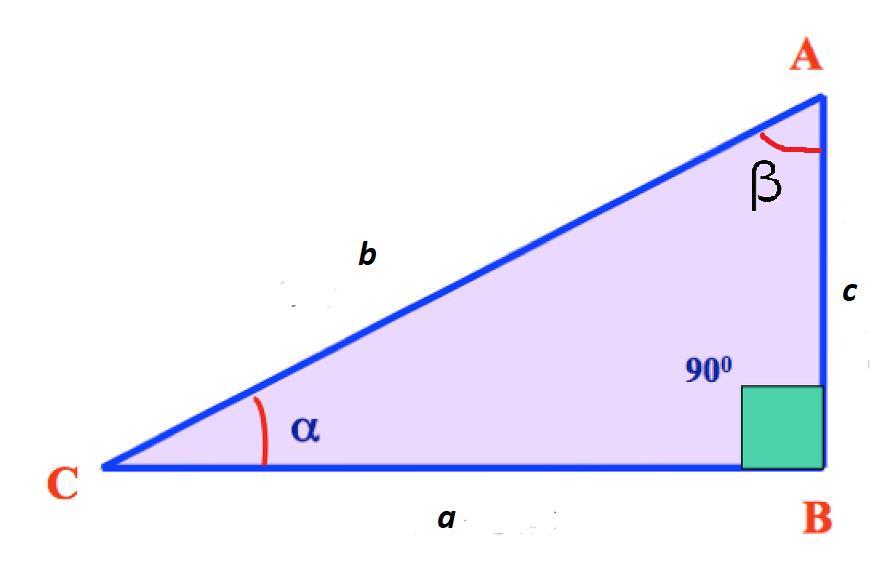
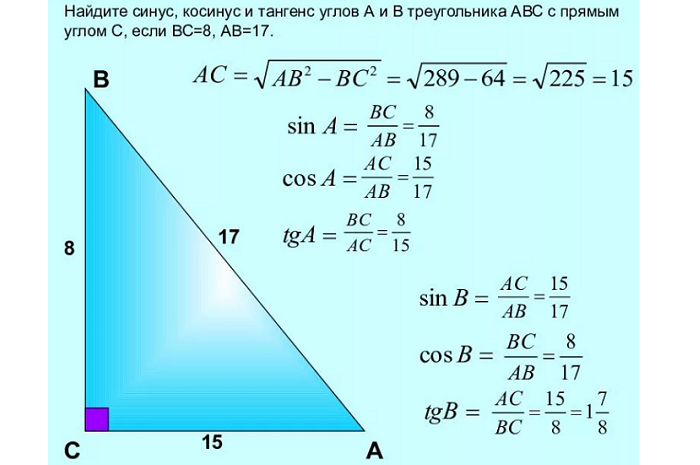
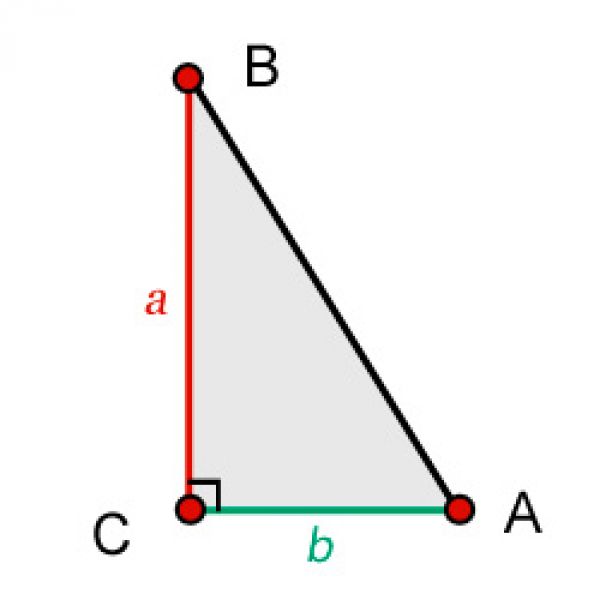
Косая сторона — это противоположная (наибольшая) сторона прямого угла; в треугольнике это сторона AC. Катетеры — это две другие стороны рядом с прямым углом; в треугольнике это BC и AB.
Что такое тангенс угла
Рисунок 1 Графики тригонометрических функций: полутон, косинус, тангенс, вторичная, сопряженная, котангенс и катагональ.
Тригонометрические функции являются одним из видов элементарных функций. К ним обычно относятся синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), sec x) и cosec x, причем последние две функции используются относительно редко (о менее часто используемых функциях см. здесь).. (Функция). В английской литературе касательные, косоугольники и косеканы обозначаются tan x, cot x и cscx. Тригонометрические функции обычно определяются геометрически, но могут быть определены детально через суммы рядов или как решения определенных дифференциальных уравнений. Это позволяет распространить определение этих функций на комплексные числа.
Содержание
Геометрическое определение
Тригонометрические функции обычно определяются геометрически. Пусть будет декартова система координат на плоскости и окружность радиуса R с принципом O в качестве центра. Пусть угол измеряется как поворот от положительного направления горизонтальной оси к лучу OB. Направление против часовой стрелки является положительным, а направление по часовой стрелке — отрицательным. Обозначим через xB и покажем его упорядоченным по yB (см. рис.)
Рис. 3. Тригонометрические функции угла α с радиусом, равным 1.
Благодаря схожим свойствам формы, очевидно, что значение тригонометрической функции не зависит от радиуса окружности R. Во многих случаях этот радиус принимается равным значению единичного отрезка, а синусоида — это просто прямой угол y.B Синус — это отклонение xB. На рисунке 3 показана величина тригонометрической функции единичного круга.
Когда a вещественно, синус a в математическом анализе — это синус угла, радиальное измерение которого равно a, как и для других тригонометрических функций.
Определение тригонометрических функций для острых углов
Во многих предыдущих учебниках по геометрии тригонометрическая функция острого угла определяется как отношение сторон прямоугольного треугольника. Пусть OAB — треугольник с углом a. Итак.
Постройте систему координат, используя направление ребер линий вдоль начала координат O и OA, при необходимости измените направление (инверсия) треугольника и поместите его в первую четверть системы координат, затем постройте окружность. Для радиуса, равного косой грани, сразу видно, что определение этой функции дает тот же результат, что и предыдущее определение. Это определение имеет ряд педагогических преимуществ, так как не требует введения понятия системы координат, но имеет и серьезный недостаток: нельзя определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении базовых задач. тупоугольные треугольники (см. теорема о полутонах, теорема о коэффициентах).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинуса и полутона можно определить как четные (полутон) и нечетные (синус) решения дифференциальных уравнений.
R(\varphi) = — R(\varphi),» width=»» height=»»/>
Если начальное условие cos(0) = sin'(0) = 1, то есть производная второго порядка берется как функция переменной, равной самой функции, со знаком минус.
Определение тригонометрических функций как решений функциональных уравнений
Функции кокерина и синуса можно определить как непрерывные решения (f и g соответственно) системы интересных уравнений: f(x+y)& amp; amp; f(x)f(y)-g(x(x))-g(y)™ g(x+y)& amp; amp; «width =» «height =» »/>
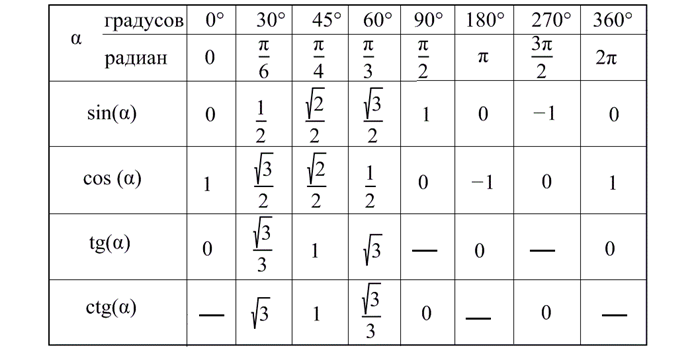
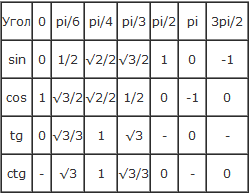
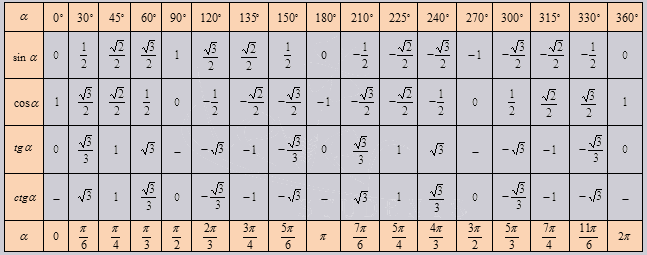
Значения тригонометрических функций для некоторых углов
Значения синуса, зм, тангенса, котескида, вторичного и конкретного углов приведены в таблице.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \,\!» width=»» height=»»/> | \,\!» width=»» height=»»/> | \,\!» width=»» height=»»/> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \,\!» width=»» height=»»/> | \,\!» width=»» height=»»/> | \,\!» width=»» height=»»/> |
| α градусов | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| α радиан | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| tg α | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctg α | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
Что такое синус?
Половина угла (sin) — это отношение противоположной ноги (противоположной стороны угла) к подчиненной (максимальной стороне, противоположной углу).
В примере sin a = bc/ac.
Что такое косинус?
Косинус угла (cos) — это отношение прилежащего перпендикуляра (рядом с углом) к подчиненному (наибольшая сторона, противоположная прямому углу). В данном примере cos a = ab/ac.
Угловой тренер (CTG) — это отношение смежных катетов (рядом с углом) к противоположным катетам (напротив угла). В примере CTG A = AB / BC. Заметим, что котоген является «тангенциальной обратной» (смежная обратная делится на противоположную), т.е. CTG a = ab / bc, а tg a = bc / ab (противоположная делится на смежную).
Если начальное условие cos(0) = sin'(0) = 1, то есть производная второго порядка берется как функция переменной, равной самой функции, со знаком минус.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших \(360°\) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Рассчитайте \(tg \:0 \).Решение. Чтобы найти касательную к нулю, сначала нужно найти синус и косинус ⌘(0 \). Вы увидите, что и те, и другие используютсяКруг из треугольников. :.
Точка ⌘ (0 \) числовой окружности совпадает с точкой ⌘ (1 \) на оси косинусов, поэтому (cos \: 0 = 1 \). Вычитая перпендикуляр к оси синусов из точки ⌘ (0 \) числового цикла, приходим к точке ⌘ (0 \). Следовательно, ዄ (tg \: 0 = \) ዄ (ዄ frac) ዄ (= \) ዄ (ዄ frac) ዄ (= 0 \).
Пример. \Вычислить \(tg \: (-765^< circ)>).Решение. \Вычислите синус и косинус \(tg \: (-765^\ circ) = \)\(Lo_765^°F)\(-765^°F)Lo_765^F)Lo_765^F). Спроектируйте \(-765^°\) в треугольном цикле. Для этого нам нужно повернуть в отрицательную сторону на ⌘ (720^°\), затем еще на ⌘ (45^°\).
Однако вы также можете определить касательные непосредственно через треугольный цикл, проведя дополнительные оси.
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Ось тангенса фактически является копией оси синуса, только со сдвигом. Поэтому все числа в нем располагаются так же, как и на оси синуса.
Чтобы определить тангенс с помощью числовой окружности, нужно: 1) Отметить соответствующую аргументу тангенса точку на числовой окружности. 2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов. 3) Найти координату пересечения этой прямой и оси тангенсов.
Пример. \Вычислите \(tg \:Lo_ frac \).Решение. 1) Окружите себя вниманием ᢙᢙᢙᢙᢙᢙᢙᢙ.
2) Проведите прямую линию через эту точку и авторитет.
3) В этом случае нет необходимости находить координаты, так как они равны \(1 \).
Пример. \Вычислите \(tg \:45°)™ и Ў(tg \:-240°)Ў.Решение. Для угла ⌘ (45°\) (⌘ (坐地\)) касательная линия будет ⌘ (1 \). Она пересекает касательный вал. А для угла ⌘(-240°\) (⌘(∠KOB\)) касательная линия равна ⌘(- \ sqrt \) (приблизительно ⌘(-1,73 \)).
Знаки по четвертям
Использование касательных валов облегчает определение признаков4-й треугольного цикла. Для этого возьмите точки квадрата и определите знаки касательных, используя метод, описанный выше. Одни и те же знаки имеют одни и те же символы.
Например, на этой диаграмме показаны две зеленые точки в кварталах I и III. В этих случаях значения касательных положительны (зеленая пунктирная линия — положительная часть оси). Поэтому в любой момент в I и III кварталах значения касательных также положительны (знак плюс). Две фиолетовые точки в четвертях II и IV похожи, но со знаком минус.
Термины «касательная» (от лат. tangent — см.) и «секущая» (от лат. secant — квадратичный) были введены датским математиком Томасом Финке (1561-1656) в его книге Geometriarotundi (1583).
Тригонометрические функции и их значение в изучении геометрии
Тригонометрические функции играют особую роль в геометрии, определяя, как соотносятся между собой стороны и углы правильного треугольника. Конечно, тригонометрия не была статичной, и время Евклида было далеко вперед, что позволило выразить эти функции путем решения дифференциальных уравнений.
Сегодня для основных тригонометрических функций используется шесть обозначений, причем четыре из шести функций являются последними в ряду и могут быть определены способами, отличными от геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc)
Рассмотрим сам правильный треугольник. Названия его сторон и углов во всех справочниках, как обычно, стандартные — по обе стороны от плоскости.
Треугольник имеет три угла, обозначаемые α, β и γ. γ всегда равен 90°. Другая сторона прямого угла γ называется гипотенузой и обозначается C. Угол α, с которого начинаются все вычисления, лежит на стороне α/ BC /, называемой противоположной стороной этого угла, и на стороне b/. AC / касательная к этому углу называется стороной касания.
Согласно евклидовой теории, которая по-прежнему актуальна (и всегда актуальна), сумма углов таких треугольников на одной плоскости равна 180 или числу пи. И для любого заданного значения угла между 0 и π/2.
Тригонометрические функции могут быть выражены через размеры сторон этого треугольника. Поскольку угол α является первым как в греческом алфавите, так и в треугольнике, мы начинаем знакомство с функциями с этого угла.
Эти функции также можно представить в виде окружностей, определив систему координат. Дана система координат с центром O. Угол, на который поворачивается часть O, показанная на диаграмме, произволен и называется θ.
Тогда касательная к этому углу θ представляет собой отношение правого конца точки A к ее дистальному концу. Таким образом, если ctgα= b:α, AC =sinθ и OS =cosθ, то tgθ=sinθ:cosθ. Аналогично, ctgθ= cosθ:sinθ или 1:tgθ.
Тангенс — это отношение…
Таким образом, существует два определения.
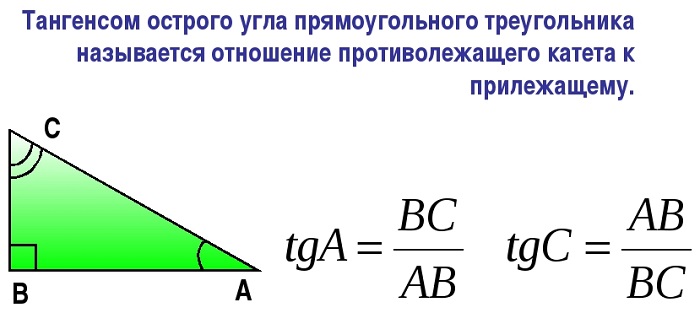
Тангенс острого угла прямоугольного треугольника — это отношение перпендикуляра к соседнему треугольнику.
Тангенс — это отношение синуса к косинусу.
Вместо «касательная к углу альфа» пишется tga. В калькуляторах и различных программах для компьютеров и ПК распространено другое название: tan(a).
Применение функции тангенса для решения задач
Чтобы научиться пользоваться этой функцией, попробуйте решить несколько примеров ее использования.
Пример: у вас есть два катетера с BC =7 см и AC=12 см. Все остальные факты о треугольниках должны быть известны.
Первое уравнение — tgα= α:β. Тогда tgα = 7:12 = 0, 5833, затем используйте массив Брадиса для нахождения угла α. На пересечении градусов и минут находится самое близкое значение угла — 0,5844. Это соответствует 30° и 18′.
Найдите ближайшее значение 3 ‘поправки. Отведите от угла и получите угол α = 30°15′. Предполагая, что сумма всех углов не должна превышать 180°, найдите второй угол с контракцией угла γ = 90°. Тогда угол β = 90°-30°15′ = 59°45’.
Осталось найти нижнее значение c.
Мы можем найти его через грех а. Это равно a:c, тогда c = a:sin a.
Используйте таблицу Бразиса для нахождения sin. Ближайшее значение для 30°36′ равно 0,5060, затем 3′ и в соответствии с полем коррекции равно 0,0008. Прибавьте это число к найденным значениям: 0, 5060 + 0,0008 = 0,5068. Подставьте это значение в формулу c = 7: 0,5068, c = 13, 8 см. Проблема решена.
Мы можем найти значение угла через значение p, которое равно 180°. Далее тангенс 30°, тангенс 0°, тангенс 60°, тангенс 90°, тангенс 45°, тангенс 15° и тангенс 75° намного проще.. Следует отметить, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет особого значения.
Вы можете найти касательные к пятиградусным углам, которые равны 0, 0875 и могут быть добавлены или удалены от наиболее распространенных углов. Например, при угле 45 градусов ее тангенс равен 1, тогда тангенс при 50 градусах равен 1, 0875; тангенс при 35 градусах можно вычислить, добавив к тангенсу при 30 градусах 5 градусов; тангенс при 10 градусах равен 10 градусам. В два раза больше угла в 5 градусов.
Для удобства приведена расчетная таблица больших углов через цену P
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Следует помнить, что если угол больше 90 градусов, то функция имеет возможность повторения. Таким образом, если вы ищете тангенс 145 градусов, 180 — 145 = 35 градусов, но со знаком «минус». Как будет понятно из конструкции круга с положительными или отрицательными значениями для абсциссы и ординаты. Научиться быстро пользоваться таблицей Брадиса и вычислять цену треугольника совсем не сложно. Главное — понять природу процесса.
Рассмотрим сам правильный треугольник. Названия его сторон и углов во всех справочниках, как обычно, стандартные — по обе стороны от плоскости.
Что такое тангенс в прямоугольном треугольнике
Полутон угла треугольника является причиной стороны, противоположной определенному углу нижней части треугольника, а косинус — причиной стороны, следующей за подчиненной.
Затем, если вы разделите угловой полутон на косинус, вы возьмете тангенс (обозначенный как TG), а если вы разделите косинус на синус, вы возьмете цыпленка. Здесь все очень просто. Главное — знать кривые и треугольники треугольника.
Также на графике в конце есть треугольные касательные, которые являются различиями между II указателями, но в данной статье они рассматриваться не будут, так как имеют лишь косвенное отношение к треугольникам.
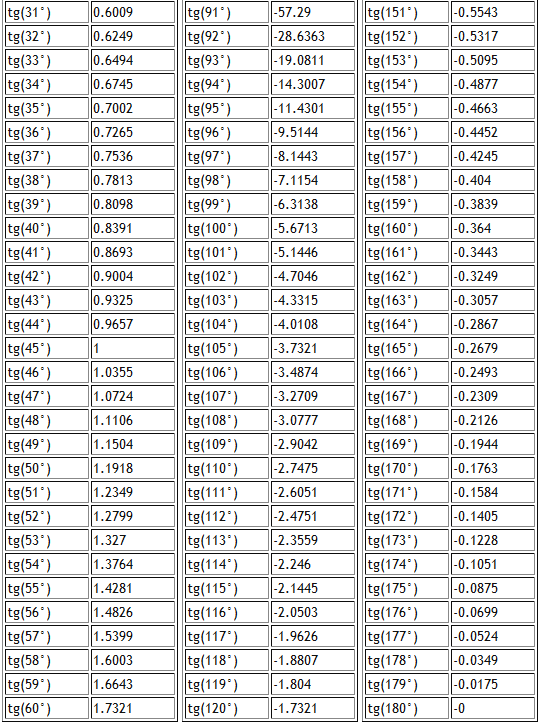
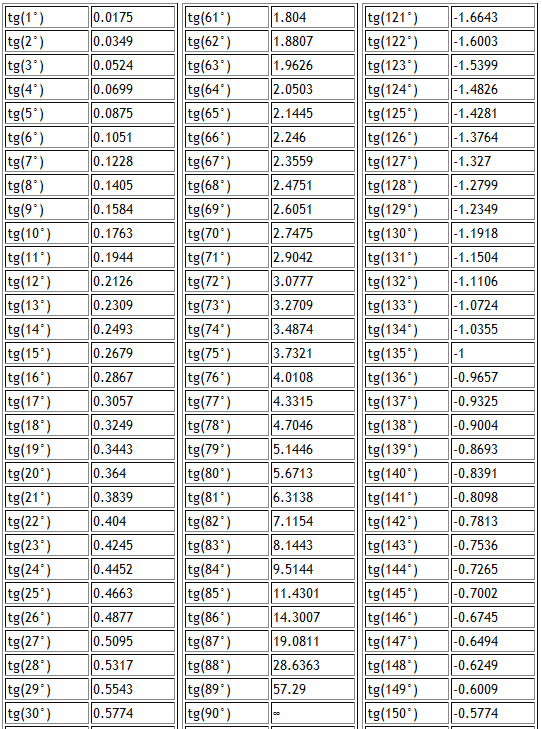
Таблица тангенсов углов от 0° до 360°
Ниже приведена таблица цен. Это поможет вам быстро найти нужную цену.
В качестве альтернативы вы можете поискать цены в Интернете или запомнить их. Наиболее эффективным методом для математиков являются печатные цены, но это непрактично для всех.
Примеры вычислений тангенса в прямоугольном треугольнике
Существует несколько методов и простых видов нахождения прямоугольных треугольников, касательных к прямоугольнику. Однако мы рассмотрим лишь некоторые из них.
Секрет здесь прост, ведь все методы ограничиваются нахождением сторон — если вы знаете значения всех сторон, то тангенс угла A треугольника находится по следующему правилу: TGA = BC:AC, что означает, что TG A равен отношению противоположных смежных сторон.
Самое простое, что вы можете сделать, это найти касательную линию острого угла. Даже если это не угол прямоугольного треугольника, его можно легко добавить к прямоугольному треугольнику.
В этом суть касательных, но если нужно найти стороны, то это, конечно, не проблема касательных.
Тангенс и котангенс. Формулы и определение
Помимо синуса и косинуса в тригонометрии имеется еще огромное количество функций, в частности, тангенс и котангенс, о котором мы поговорим на данном уроке.
Тангенс tg(x) — это отношение синуса sin(x) к косинусу cos(x)
Определения для прямоугольного треугольника:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Определения для числа:
Так как делить на ноль нельзя, то значения в знаменателе не может быть равным нулю, т.е.
\( ctg\ x = \dfrac
Таблица знаков тангенса и котангенса по четвертям (составить ее можно, опираясь на таблицу синусов и косинусов, применяя правило деление чисел с отрицательными знаками):
| I | II | III | IV | |
| tg x | + | – | + | – |
| ctg x | + | – | + | – |
Как видите, значения тангенса и котангенса очень просто найти, зная значения синуса и косинуса, тем не менее также существует таблица и для данных функций, которая существенно упрощает жизнь. Здесь я представлю самые распространенные значения. А для всех остальных значений существуют специальные таблицы Брадиса.
| \( \frac<\pi> <6>\) | \( \frac<\pi> <4>\) | \( \frac<\pi> <3>\) | \( \frac<\pi> <2>\) | 0 | |
| tg x | \( \frac<\sqrt<3>> <3>\) | 1 | \( \sqrt <3>\) | – | 0 |
| ctg x | \( \sqrt <3>\) | 1 | \( \frac<\sqrt<3>> <3>\) | 0 | – |
Завершая разговор про данные тригонометрические функции нельзя не сказать про еще две важные формулы:
Для любого допустимого значения х справедливы равенства:
Для любого допустимого значения х также справедливы следующие равенства:
Ну вот теперь вроде все, более подробно и углубленно изучать мы будем все функции в процессе дальнейшего обучения.
Тангенс угла
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/c
cosA = b/c
Формула тангенса
tg A = a/b
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
Тангенс
Смотреть что такое «Тангенс» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
Тангенс угла это отношение чего? Основы тригонометрии
Определение

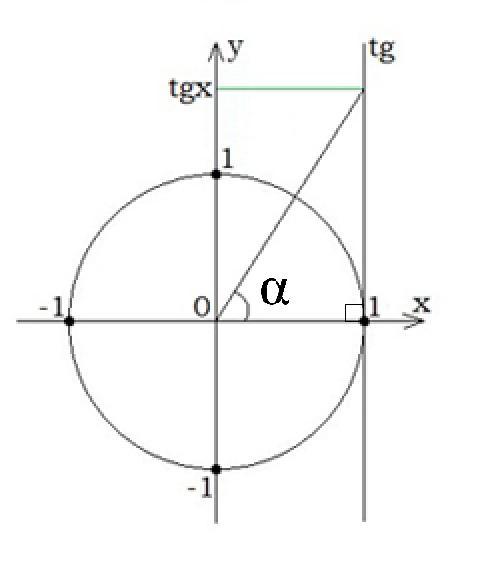
Теперь перейдем к определению тангенса, которое несет алгебраический смысл, для этого нам понадобится единичная окружность.
Для того чтобы отметить в декартовой системе координат численное значение тангенса необходимо для начала провести прямую х = 1, которая будет перпендикулярна оси абсцисс и параллельна оси ординат. После чего отложим от оси абсцисс угол альфа и продлим его сторону до пересечения с прямой х = 1. Ордината точки пересечения в конкретной ситуации будет являться численным значением тангенса отложенного угла.
Как связаны тангенс с котангенсом?
Тангенс является обратной функцией от котангенса, а это значит что: tg = 1/ctg. Таким образом, отношение тангенса к котангенсу является равным единице: tg/ctg = 1.
Существует ли связь тангенса с косинусом?
Существует такое тождество, определяющее связь этих двух тригонометрических функций: 1 + tg2 = 1/cos2. Попробуем доказать это тождество, преобразуя его левую часть с помощью алгебраического определения тангенса:
Теперь приведем выражение к общему знаменателю:
Вспомним главное тригонометрическое тождество и упростим выражение, после чего получим:
Эта дробь является равной правой части данного изначально выражения, таким образом мы доказали тождество.
Заключение
Геометрические фигуры завораживают количеством своих свойств и функций, таких как тангенс в прямоугольном треугольнике. Это происходит в основном из-за двух факторов.
Во-первых, нам уже известен один из углов, который равен 90 градусам. Во-вторых, есть много свойств с применением прямоугольников. А из двух прямоугольных треугольников как раз получается именно такая фигура.
Из этого вытекает многое, но сегодня мы поговорим об одном очень интересном свойстве такого треугольника, как тангенс. В данной статье мы подробно рассмотрим определение тангенса, узнаем, как его можно найти и как его можно использовать.
Что такое тангенс в прямоугольном треугольнике
Также бывают и тригонометрические тангенсы на окружности со своими графиками, разностью показателей числа π, но в данной статье мы их не рассматриваем, так как к треугольнику они имеют лишь косвенное отношение.
Таблица тангенсов углов от 0° до 360°
Ниже представлена таблица значений, которая пригодится для быстрого нахождения необходимых значений.
В качестве альтернативы предлагаем либо искать значения онлайн, либо запоминать их. Самым же эффективным способом математики считают вывод этих значений, но это будет удобно далеко не для всех.
Примеры вычислений тангенса в прямоугольном треугольнике
Существует довольно много способов и несложных формул для нахождения тангенса в прямоугольном треугольнике. Мы же рассмотрим только некоторые из них.
Легче всего найти тангенс именно острого угла. Если даже это не угол прямоугольного треугольника, то дополнить его до прямоугольного не составит труда.
Это то, на чем построена сама сущность тангенса, но если нужно найти стороны, то это уже точно задача не про тангенсы.
Что такое тангенс?
В тригонометрии существует несколько основных (базовых) понятий, которые проходятся в средней школе и выносятся на ЕГЭ. В их число входит тангенс.
Определение функции.
В учебниках дается точное определение термина «тангенс», только к нему добавляется загадочное «угла х». Итак, тангенс угла – это отношение противолежащего катета к прилежащему. Например, tgx = а/b.
Чтобы разобраться с определением, необходимо вернуться к истокам тригонометрии и нарисовать угол.
Для этого нарисуем треугольник с прямым углом, стороны которого, прилегающие к углу в 90 градусов – т.е. катеты, назовем «а» и «b», а гипотенузу – «с».
Соотношение противолежащего (короткого) катета к прилежащему (длинному) будет равно: а/b. В цифровых значениях это может быть 3/4 или 4/5.
Интересно, что, если продлить длину сторон прямоугольного треугольника, сохранив значение острого угла, то размер (величина) сторон, конечно, поменяется (это будут уже не «а», «b», и «с», а «l», «m», «n»). Но соотношения между сторонами останется прежним.
Например, отношение «а» к «b» было равным 3/4, после удлинения сторон соотношение m/n стало равно 6/8. Но 6/8 = 3/4.
Заметив эту интересную закономерность, древние вывели правило: соотношения сторон треугольника с прямым углом не зависят от длин его сторон, если не меняется острый угол.
При чем тут угол?
В определении понятия «тангенс» обязательно есть часть «угла». Зачем, если речь идет о соотношении сторон прямоугольного треугольника?
Отвечаем: если изменить острый угол прямоугольного треугольника, например, с 25 градусов, на 30, то все соотношения поменяются вместе с ним.
Если ранее дальний катет к прилежащему мы обозначали через 3/4, то новое соотношение будет равно уже иным значениям. Например, 6/4.
Отсюда вывод: соотношения между сторонами не зависят от их длины, но зависят от величины острого угла.
Интересно, что у каждого угла в прямоугольном треугольнике есть свои значения тангенса, так же как синуса, косинуса, котангенса.
Поэтому если в задаче на ЕГЭ Вам дан размер угла, то это автоматически означает, что значения его тригонометрических функций Вам уже известны. Также по значению тангенса или иной функции можно найти угол.
Таблицы Брадиса.
Разумеется, обычному человеку не под силу запомнить все значения тригонометрических функций. Для того чтобы облегчить жизнь математиков эти значения были сведены в специальные тригонометрические таблицы. В них для каждого возможного угла в прямоугольном треугольнике прописаны его тригонометрические функции.
Такие таблицы имеют название «Таблицы Брадиса». Они были составлены без применения калькуляторов и помогали ученым в расчетах.
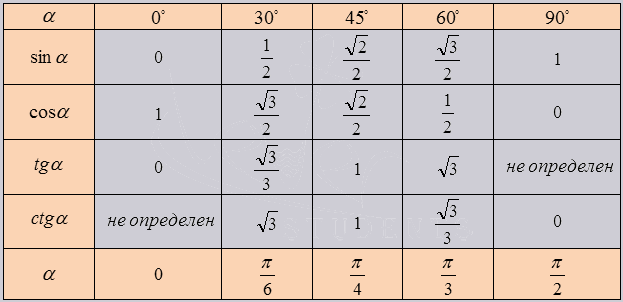
В школьной программе обычно требуется запомнить наизусть значение функций для нескольких углов:
Что такое тангенс угла
Чтобы сформулировать определение тангенса угла и других тригонометрических функций, рассматривают соотношение углов и сторон в прямоугольном треугольнике.
Известно, что сумма углов любого треугольника равна 180°. Следовательно, в прямоугольном сумма двух непрямых углов равна 90°. Стороны, образующие прямой угол, называются катетами. Третья сторона фигуры — гипотенуза. Каждый из двух острых углов прямоугольного треугольника образован гипотенузой и одним катетом, который называется «прилежащим» для этого угла. Соответственно, другой катет называется «противолежащим».
Тангесом угла называется отношение противолежащего катета к прилежащему. Попутно легко запомнить, что обратное отношение называется котангенсом угла. Тогда тангенс одного острого угла прямоугольного треугольника равен котангенсу второго. Также очевидно, что тангенс угла равен отношению синуса этого угла к его косинусу.
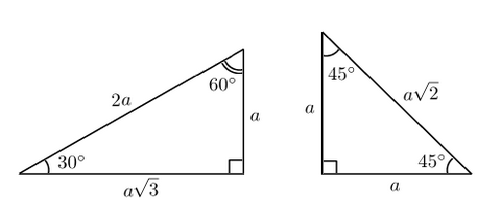
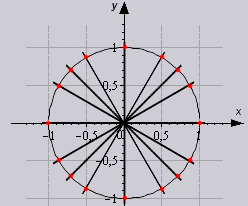
Чтобы узнать, какие значения может принимать тангенс угла, начертите единичную окружность. При изменении угла от 0° до 90° тангенс изменяется от нуля и устремляется в бесконечность. Изменение функции нелинейное, на графике легко найти промежуточные точки для построения кривой: tg 45°=1, tg30°= 1/√3, tg60°=√3.
ТАНГЕНС
— одна из тригонометрических функций:
Т. разлагается в ряд
Смотреть что такое «ТАНГЕНС» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
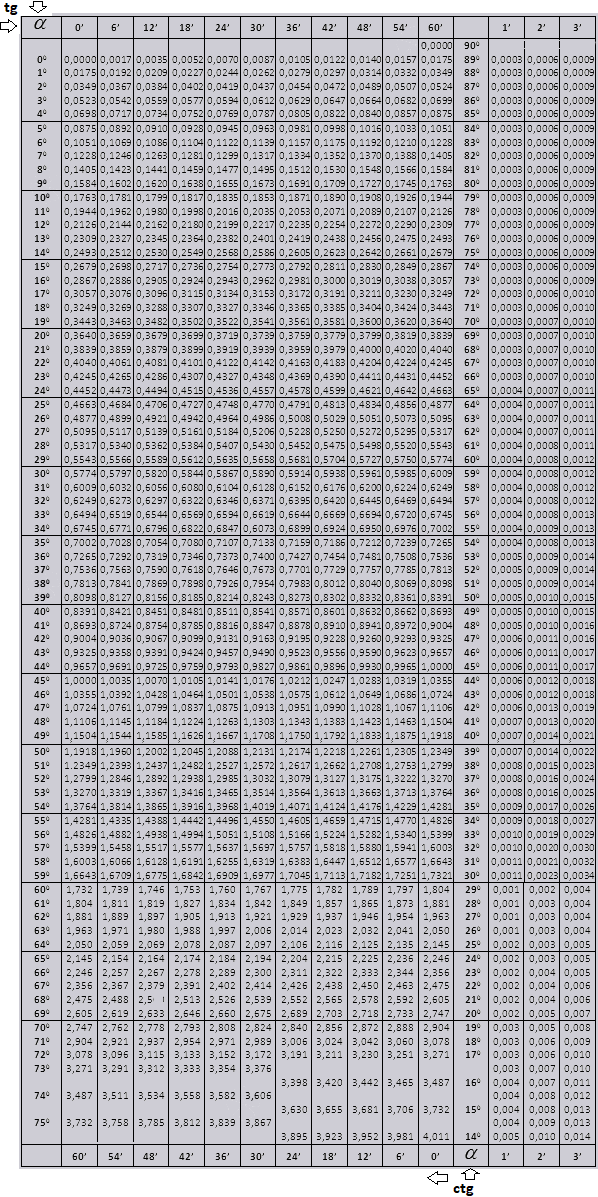
Таблица тангенсов углов (углы, значения)
В таблице значения тангенсов от 0° до 360°. Таблица тангенсов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен тангенс угла, просто найдите его в таблице. Для начала короткая версия таблицы:
Таблица тангенсов для 0°-180°
|
|
|
|
|
|
Существуют также следующие таблицы тригонометрических функций по геометрии: таблица синусов, таблица косинусов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица тангенсов углов (углы, значения)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
ТАНГЕНС
Смотреть что такое «ТАНГЕНС» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
Тангенс в прямоугольном треугольнике
Что такое тангенс в прямоугольном треугольнике? Как найти тангенс? От чего зависит значение тангенса?
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Например, для угла A треугольника ABC
Поэтому тангенс угла A в треугольнике ABC — это

противолежащим является катет AC,
Соответственно, тангенс угла B в треугольнике ABC
равен отношению AC к BC:
Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета.
Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Тангенс угла треугольника зависит от величины угла, но не зависит от катетов (важно лишь их отношение).
Если в треугольнике изменить длины катетов, не меняя угол, то величина тангенса не изменится.
Таблица тангенсов
Современные определения тригонометрических функций и их символика принадлежат Л. Эйлеру. Хотя еще в 3-м в. до н. э в трудах Архимеда, Евклида и других рассматриваются отношения сторон в прямоугольном треугольнике, что фактически и является тригонометрическими функциями. В переводе с греческого тригонометрия означает «треугольник» и «измеряю» и является разделом математики, изучающим связь между сторонами и углами треугольника. Как нам известно, в прямоугольном треугольнике 2 угла острых, а один является прямым. Стороны треугольника, прилежащие к углу, равному 90 градусов, называются катетами, с сторона напротив прямого угла является гипотенузой. Тангенс представляет собой одну из тригонометрических функций угла. Функцию тангенс для острых углов можно рассматривать как отношение двух катетов: противолежащего к прилежащему.
tg (a)=а/в
где а — катет, противолежащий углу а;
в — прилежащий катет.
Тангенс заданного угла можно определить, воспользовавшись таблицей Брадиса, где помещены тригонометрические функции всех углов. Если в задаче известна величина угла и одна из сторон треугольника, будет несложно определить остальные его стороны и углы. С помощью онлайн калькулятора ваши расчеты будут более быстрыми и правильными.
Здесь четырехзначные математические онлайн таблицы для таких тригонометрических функций как: синусы, косинусы, кроме того вы на нашем сайте вы сможете найти подобные таблицы для тангенсов и котангенсов.
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
Таблица Брадиса.
Таблица разбита на 2 части. В 1-ой части таблицы Брадиса тангенсы от 0° до 75° и котангенсы от 15° до 90° определяются с помощью дополнительных столбиков для 1’, 2’ и 3’ (минуты). Во 2-ой части тангенсы от 75° до 90° и котангенсы от 0° до 15° записаны в таблице с точностью до 1’ угла.
Тангенс угла
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/c
cosA = b/c
Формула тангенса
tg A = a/b
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.

ТАНГЕНС
Смотреть что такое «ТАНГЕНС» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
Таблица тангенсов
Тангенсом угла называется отношение синуса этого угла к косинусу:
Таблица тангенсов — таблица, содержащая значения тангенсов углов. В нашей таблице вычислены тангенсы углов от 1° до 180°.
Таблицы тангенсов можно использовать при отсутствии калькулятора с тригонометрическими функциями.
Таблица тангенсов углов 0°, 30°, 45°, 60°, 90°
Замечание: тангенс 90° не определён, так как .
Чему равен тангенс угла
Здравствуйте!
Чему равен тангенс угла. Нужны хотя бы начальные сведения.
Спасибо!
Вопрос о том, чему равен тангенс угла, будем рассматривать на прямоугольном треугольнике.
Рассмотрим прямоугольный треугольник, катеты которого обозначим, как katet1 и katet2, а гипотенузу — gipotenuza.
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего к этому углу катета к прилежащему катету, то есть длину противолежащего катета нужно разделить на длину прилежащего.
Поскольку у прямоугольного треугольника только один угол прямой, а остальные два — острые, то можно записать две формулы для тангенсов этих двух углом.
Посмотрим на рисунок.

Запишем формулу для тангенса угла 1:
Формула для тангенса угла 2:
Также при решении тригонометрических задач используют наиболее распространенные значения тангенсов от некоторого набора углов. Например, такими углами принято считать 0 градусов, 30 градусов, 45 градусов, 60 градусов и 90 градусов. Также в качестве аргумента функции тангенс используют кроме углов в градусах значение углов в радианах.
Приведем значения некоторых основных значений тангенсов, взяв в качестве аргументов углы и в градусах, и в радианах:
тангенс
Смотреть что такое «тангенс» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
Значение слова «тангенс»
[От лат. tangens — касающийся]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ТА’НГЕНС, а, м. [латин. tangens — касающийся] (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
та́нгенс
1. одна из тригонометрических функций угла, равная в прямоугольном треугольнике отношению катета, противолежащего углу, к катету, прилежащему к нему ◆ Ведь тангенс при девяноста градусах, взмыв к бесконечности, тут же и рушится в пропасть минус бесконечности. Солженицын, «В круге первом», 1968 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова возданный (прилагательное):
Ассоциации к слову «тангенс»
Синонимы к слову «тангенс»
Предложения со словом «тангенс»
Цитаты из русской классики со словом «тангенс»
Понятия, связанные со словом «тангенс»
Отправить комментарий
Дополнительно
Предложения со словом «тангенс»
Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат.
Его метод разработки таблиц синуса и тангенса дал результаты с точностью до восьмой десятичной запятой.
Соответственно узнаем, что такое функции активации, реализуем самые распространённые из них, такие как – единичная функция, сигмоида, RELU, гиперболический тангенс, Softmax.
В каких пределах находится тангенс. Синус, косинус, тангенс: что такое? Как найти синус, косинус и тангенс
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Синус, косинус и тангенс острого угла прямоугольного треугольника.
Приветствую Вас дорогие учащиеся.
Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Это тема не сложная, главное это запомнить правила. И так начнем:
Вспомним, что такое прямоугольный треугольник?
Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.
Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;
Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;
Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;
Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;
Пусть дан прямоугольный треугольник ABC с прямым углом C.


Аналогично рассуждаем относительно угла B.


Пример:
Найти тангенс угла С (tg(C)) треугольника ABC.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Тригонометрическая таблица
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Синус и косинус
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Тангенс угла tg(A)
Формула тангенса угла tg(A) имеет следующий вид:
Калькулятор для вычисления:
Тангенс угла 0 градусов:
Тангенс угла 30 градусов:
Тангенс угла 45 градусов:
Тангенс угла 60 градусов:
Тангенс угла 90 градусов:
Тангенс
Смотреть что такое «Тангенс» в других словарях:
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
ТАНГЕНС
Полезное
Смотреть что такое «ТАНГЕНС» в других словарях:
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (от лат. tangens касающийся) одна из тригонометрических функций … Большой Энциклопедический словарь
ТАНГЕНС — ТАНГЕНС, тангенса, муж. (лат. tangens касающийся) (мат.). Тригонометрическая функция угла, равная в прямоугольном треугольнике отношению катета, лежащего против данного острого угла, к другому катету. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова
ТАНГЕНС — ТАНГЕНС, а, муж. Тригонометрическая функция, равная отношению синуса к косинусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ТАНГЕНС — муж., лат., геом. касательная; прямая черта, коснувшаяся дуги в одной точке. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
тангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
тангенс — тангенциальный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы тангенциальный EN tangent … Справочник технического переводчика
тангенс — а; м. [от лат. tangens касающийся] Матем. Тригонометрическая функция, равная отношению синуса к косинусу. Найти, вычислить т. График тангенса. * * * тангенс (от лат. tangens касающийся), одна из тригонометрических функций. * * * ТАНГЕНС ТАНГЕНС… … Энциклопедический словарь
ТАНГЕНС-БУССОЛЬ — Прибор для измерения силы гальванического тока. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС БУССОЛЬ инструмент для измерения силы гальванич. тока посредством отклонения им магнитной стрелки. Словарь… … Словарь иностранных слов русского языка
Тангенс острого угла
Здравствуйте!
Что такое тангенс острого угла? Как его можно найти? Желательно на примерах.
Спасибо!
Понятие «тангенс острого угла» (как и некоторых других тригонометрических функций) обычно связывают с прямоугольным треугольником.
Для определения тангенса с помощью прямоугольного треугольника будет использоваться только понятие противолежащего катета и прилежащего катета.
Объясню более просто что значат эти понятия.
Если говорить об одном из двух острых углах прямоугольного треугольника, то прилежащим к этому углу катетом будет являться тот, который создает этот угол с гипотенузой этого треугольника. Второй же катет, который не имеет общих точек с указанным углом, называется противолежащим катетом.

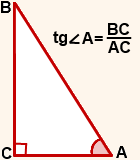
Из прямоугольного треугольника тангенс выражается как противолежащий катет, разделенный на прилежащий.
Например, из рисунка запишем чему будет равен тангенс угла А:
tg A = ВС / АС.
Запишем выражение для угла В:
tg В = АС / ВС.
Также у тангенса есть еще одно важное определение, которое используется не менее часто, чем уже рассмотренное.
Тангенс острого угла можно найти как синус этого угла, разделенный на косинус этого же угла.
Запишем выражение для тангенса углов А и В:
tg A = sin A / cos A
tg B = sin B / cos B
Рассмотрим пример.
Пример:
Найти тангенс угла В треугольника ABC, если сторона АС = 5 см, а сторона ВС = 17 см.
Решение.
Все необходимые данные есть, нужно только подставить их в формулу тангенса:
tg В = АС / ВС = 5 / 17.
Котангенс острого угла (ctg): определение, формула, таблица, график, свойства
Определение
Котангенс острого угла α (ctg α или cotan α) – это отношение прилежащего катета (b) к противолежащему (a) в прямоугольном треугольнике.
Например:
a = 3
b = 4
ctg α = b / a = 4 / 3 ≈ 1,334.
Геометрическое определение
Обратная к котангенсу функция
Арккотангенс x – это обратная функция к котангенсу x.
Если котангенс угла у равняется х (c tg y = x ), значит арккотангенс x равен у :
Таблица тангенсов и котангенсов
В данной таблице представлены значения тангенсов и котангенсов при некоторых значениях аргумента.
Периодичность
Четность
Функции тангенс и котангенс – нечетные.
Определение тригонометрических функций для острых углов
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений :
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями 



Области определения и значений, возрастание, убывание
Функции тангенс и котангенс непрерывны на своей области определения (см. доказательство непрерывности ). Основные свойства тангенса и котангенса представлены в таблице (n – целое).
| y = tg x | y = ctg x | |
| Область определения и непрерывность | ||
| Область значений | –∞ | –∞ |
| Возрастание | – | |
| Убывание | – | |
| Экстремумы | – | – |
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | – |
Понятие угла: радиан, градус
Давай посмотрим на рисунке. Вектор «повернулся» относительно точки на некую величину.
Что же ещё необходимо знать о понятии угла?
Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную части окружности.
Углом в радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
Ну что, разобрался?
Если нет, то давай разбираться по рисунку.
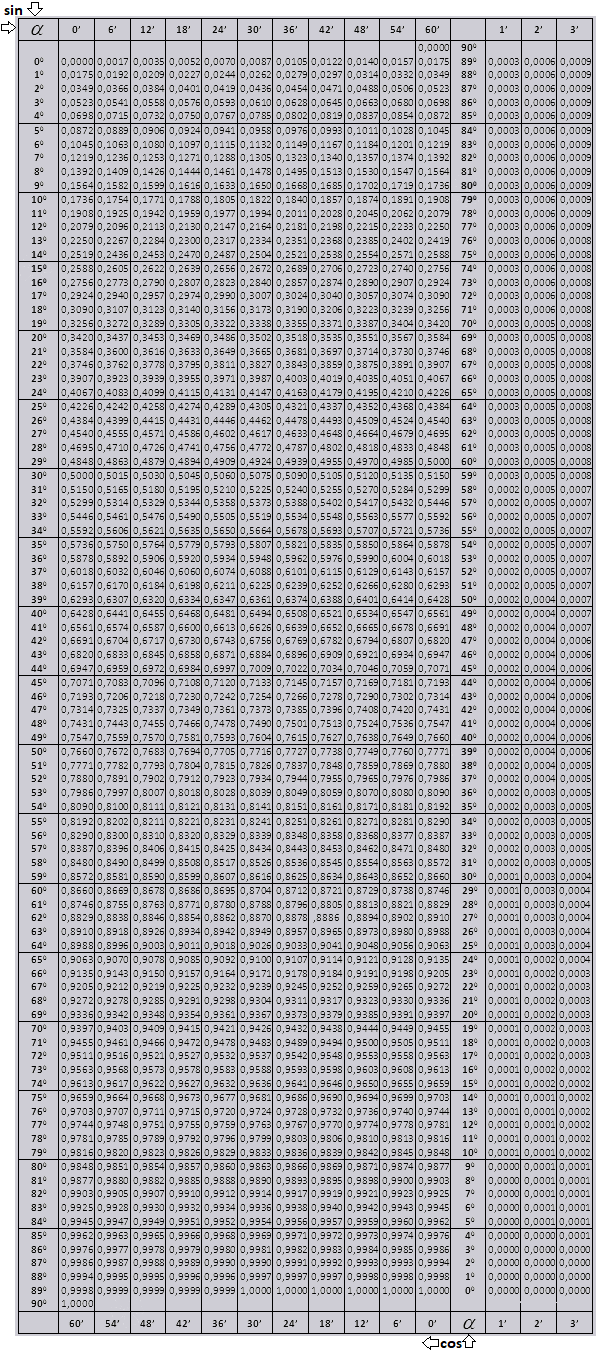
Таблица котангенсов Брадиса для углов до 75 градусов
| ctg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ |
| 0 | 90° | |||||||||||||
| 89° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 87° | 349 | 367 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 |
| 86° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 85° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0.0875 | 3 | 6 | 9 |
| 84° | 0.0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 83° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 82° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 81° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 80° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 79° | 0.1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 78° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 |
| 77° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 76° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 75° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 74° | 0.2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 73° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 72° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 71° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 70° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.364 | 3 | 7 | 10 |
| 69° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 68° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 67° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 66° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 65° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 64° | 0.4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 63° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 62° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 61° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 60° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 59° | 0.5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 58° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 57° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 56° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 55° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0.7002 | 4 | 9 | 13 |
| 54° | 0.7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 4 | 8 | 13 |
| 53° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 52° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 51° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 50° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 49° | 0.8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 48° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 47° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 46° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0.9657 | 6 | 11 | 17 |
| 45° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1 | 6 | 11 | 17 |
| 44° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 43° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 42° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 41° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 40° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1.1918 | 7 | 14 | 21 |
| 39° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 38° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 37° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 36° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 35° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1.4281 | 9 | 17 | 26 |
| 34° | 1.4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 33° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 32° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 31° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 30° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 29° | 1.732 | 1.739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1.782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 28° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 27° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 26° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 25° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 24° | 2.145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 23° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 22° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 21° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 20° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 19° | 2.747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2.888 | 2.904 | 3 | 5 | 8 |
| 18° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 17° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 16° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | 3 | 7 | 10 | |||||
| 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |||||||
| 15° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
| 3.63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |||||||
| 14° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | 4 | 9 | 13 | |||||
| 3.895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 |
Применение функции котангенса для решения задач по тригонометрии
Для понимания того, как пользоваться тригонометрическими функциями, нужно практически решить задачу с применением этих функций.
Пример: прямоугольный треугольник АВС, катет ВС = а = 8 см, катет АС = b = 13 см. Нужно найти все недостающие размеры в треугольнике.
Первая формула, которую мы применяем, это ctg α = b : а. Тогда ctg α = 13 : 8=1, 625. Затем по таблице Брадиса для функций тангенсов и котангенсов ищем наше значение котангенса. Котангенсы углов смотрим, начиная с правой стороны таблицы. Находим значение 1,6255, которое равно 30 ° 30′, но оно больше нашего на 0,0005. Можем принять его таким, а можем отнять от найденного значения поправку в 1′. Тогда угол α = 30 ° 29′. Угол β, согласно Эвклиду, будет равен: β = 90° – 30 ° 29′ = 59° 21′.
Затем ищем гипотенузу с. Гипотенузу лучше искать через функцию синуса, то есть через sin α, который равен а: с, тогда с = а : sin α.
Обращаемся к таблице Брадиса, но уже не к значению тангенсов и котангенсов, а там, где указаны значения синуса и косинуса угла.
Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 8 : 0,5068, с = 15,8 см. Задачу мы успешно решили.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как котангенс 30 градусов, котангенс 0 градусов, котангенс 60 градусов, котангенс 90 градусов, котангенс 45 градусов, котангенс 15 градусов, котангенс 75 градусов можно рассматривать намного проще. Нужно знать, что котангенс 0 градусов не существует, а котангенс 90 градусов равен 0.
Можно найти котангенс угла 5 градусов, который равен 11,83 и находится в таблице Брадиса котангенсов для малых углов и добавлять или отнимать от наиболее часто встречающихся углов. Например, угол 45 градусов, его котангенс равен 1, тогда котангенс угла 50 градусов будет равен 1+11,83 = 12,83. Котангенс 35 градусов можно рассчитать путем добавления к котангенсу 30 градусов угол 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π, которое уже рассчитано. Ниже показана таблица котангенсов и тангенсов основных углов.
| Значение угла α (градусов) | Значение угла α в радианах | ctg (Котангенс) |
|---|---|---|
| Котангенс 0 | 0 | – |
| Котангенс 15 | π/12 | 3.7321 |
| Котангенс 30 | π/6 | 1.7321 |
| Котангенс 45 | π/4 | 1 |
| Котангенс 50 | 5π/18 | 0.8391 |
| Котангенс 60 | π/3 | 0.5774 |
| Котангенс 65 | 13π/36 | 0.4663 |
| Котангенс 70 | 7π/18 | 0.364 |
| Котангенс 75 | 5π/12 | 0.2679 |
| Котангенс 90 | π/2 | 0 |
| Котангенс 105 | 5π/12 | -0.2679 |
| Котангенс 120 | 2π/3 | -0.5774 |
| Котангенс 135 | 3π/4 | -1 |
| Котангенс 140 | 7π/9 | -1.1918 |
| Котангенс 150 | 5π/6 | -1.7321 |
| Котангенс 180 | π | – |
| Котангенс 270 | 3π/2 | 0 |
| Котангенс 360 | 2π |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты.
Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса. Но можно, если это не экзамен по математике, рассчитать функцию котангенса и онлайн на сайте.
Котангенсы и тригонометрические функции, знакомство
В геометрии важную роль играют тригонометрические функции, которые объясняют, как относятся между собой углы и стороны треугольника с прямым углом. Наука не стоит на месте и развивается, так же как и тригонометрия. Есть новые решения дифференцированных уравнений, которые выражают тригонометрические функции и о которых Евклид не мог знать.
В основном, используются для вычислений значений тригонометрических функций, причем только первые из двух могут определяться только с помощью геометрии.
Синус (sin):
Косинус (cos):
Котангенс (ctg):
Тангенс (tg):
Секанс (sec):
Косеканс (cosec): 
Рассматривая прямоугольный треугольник, нужно учесть, что все справочные материалы дают одинаковое обозначение всех его параметров, таких как углы и стороны.
Три угла в нем обозначаются α, β, γ, причем угол 90° всегда обозначается γ. Сторона, лежащая напротив прямого угла, называется гипотенуза и обозначается всегда с. Альфа это первая буква греческого алфавита и угол, с которого начинаются все расчёты, также называется α. Сторона, или катет, лежащая напротив этого угла, называется противолежащей и называется а или ВС от названия вершин. Сторона, которая лежит рядом с углом или катет, называется прилежащей и обозначается b или АС.
По теории Евклида, который довел её раз и навсегда, сумма всех углов этого треугольника, который лежит в одной плоскости, равна 180°или числу π. И значения каждого угла будут находиться в промежутке между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
Синус α можно выразить через отношение катета, который противолежит углу α к гипотенузе нашего треугольника, то есть через формулу sin α = а: с.
Косинус α выражаем, соответственно, выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть через формулу sin α = а: с. Также нужно помнить, что sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α, что помогает при решении задач.
Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
Соответственно, котангенс мы выражаем аналогичным способом ctg α = b : а.
Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b, а косеканс по угла α той же теории как отношение гипотенузы треугольника к катету, который противостоит углу, cosec α = с : a.
Если задать систему координат с центром в точке О, а точка А, которая будет двигаться по окружности, образует радиус ОА. Это наглядно видно на чертеже.
Угол поворота можно считать произвольным и, согласно принятым обозначениям, называется θ. Через эту окружность можно выражать вышеназванные функции.
Например, тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Тогда если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Решение уравнения tg x = a
| Обычная форма записи решения: |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
 |  |
| tg x = – 1 |  |
 |  |
| tg x = 0 |  |
 |  |
| tg x = 1 |  |
 |  |
Решение уравнения ctg x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
Частные случаи решения уравнений ctg x = a
| Уравнение | Решение |
 |  |
| ctg x = – 1 |  |
 |  |
| ctg x = 0 |  |
 |  |
| ctg x = 1 |  |
 |  |

Свойства котангенса
Ниже в табличном виде представлены основные свойства котангенса с формулами.