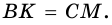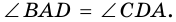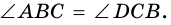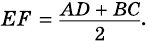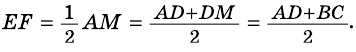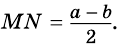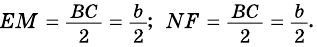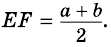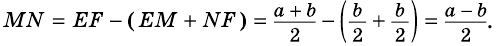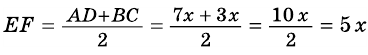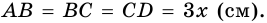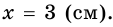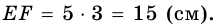Что такое трапеция
Что такое трапеция
Трапеция
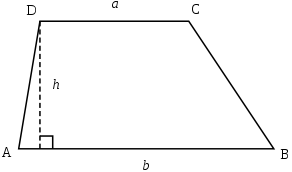
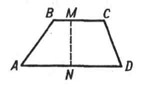
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Содержание
Связанные определения
Элементы трапеции
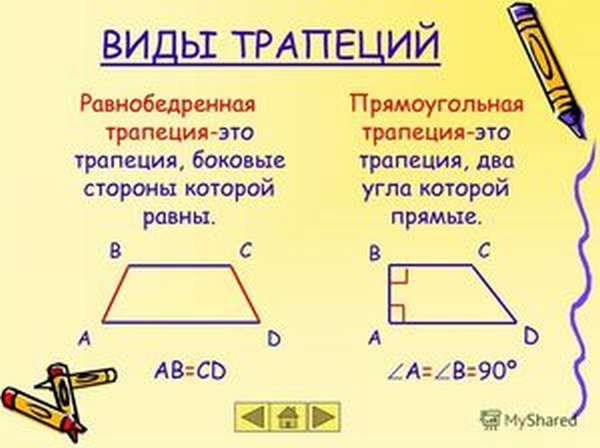
Виды трапеций
Общие свойства
Свойства и признаки равнобедренной трапеции
Вписанная и описанная окружность
Площадь
ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:
См. также
Примечания
Планигон
Полезное
Смотреть что такое «Трапеция» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Трапеция – это стол, который стал геометрической фигурой
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы решили подробно рассказать о такой геометрической фигуре, как ТРАПЕЦИЯ.
Ее подробно изучают на уроках геометрии в 8-м классе. И эти уроки являются частью общего знакомства школьников с различными четырехугольниками.
Определение трапеции
Трапеция – геометрическая фигура, которая представляет собой четырехугольник, у которого две противоположные стороны располагаются на параллельных прямых. А две другие стороны должны, наоборот, быть не параллельными.
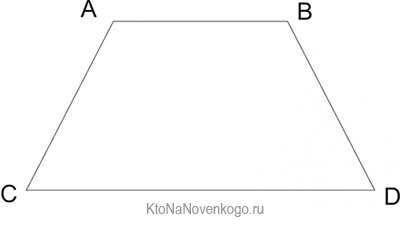
Вот так выглядит классическая трапеция:
У этой фигуры стороны АВ и CD являются параллельными. А вот AD и CB – нет.
Происхождения слова
Первое упоминание об этой фигуре встречается еще в трудах известного древнегреческого математика Евклида.
В его книге «Начала» этим термином описывается абсолютно любой четырехугольник, который не является параллелограммом.
Если кто не помнит, параллелограммом называют четырехугольник, у которого противоположные стороны параллельны. Выглядит эта фигура в классическом понимании вот так:
Интересно, что и всем известные фигуры – квадрат, прямоугольник (что это?) и ромб (это как?) – также являются частным случаем параллелограмма. Ведь действительно – у них противоположные стороны параллельны друг к другу.
И получается, что Евклид был в целом прав. Он просто поделил все четырехугольники на две большие категории – параллелограммы и трапеции.
Кстати, само слово ТРАПЕЦИЯ также имеет греческое происхождение. В древние времена оно звучало как «трапедзион». И в переводе это означает « обеденный стол». Поэтому слово «трапеза», которое у нас является синонимом любого приема пищи тоже родом оттуда.
Стороны трапеции
Парные стороны трапеций имеют свои названия:
Закрепим это с помощью рисунка:
В данном случае стороны АВ и CD параллельны друг другу. А значит, именно они являются основаниями. А вот АС и BD – наоборот, явно не параллельны. И соответственно, это боковые стороны.
Кстати, расположение сторон не зависит от расположения самой фигуры. Даже вот в таких положениях
все равно параллельные стороны будут считаться основаниями, а непараллельные – боковыми.
Равнобедренная и прямоугольная трапеции
Вариант трапеции, который мы рассмотрели – это самые распространенные виды геометрической фигуры. Но есть и частные случаи:
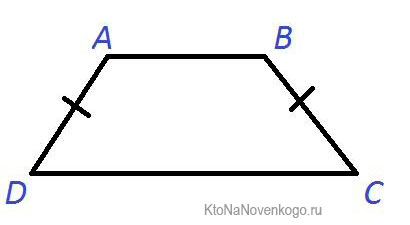
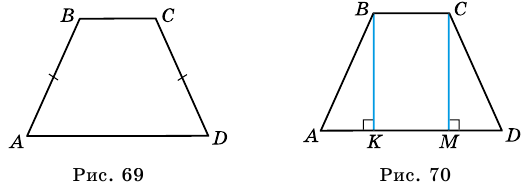
Равнобедренная трапеция – та, у которой боковые (не параллельные) стороны равны. Ее еще называют равнобокой или равнобочной.
Выглядит она вот так:
В данном примере графически показано, что стороны AD и ВС равны между собой. Об этом свидетельствуют небольшие черточки.
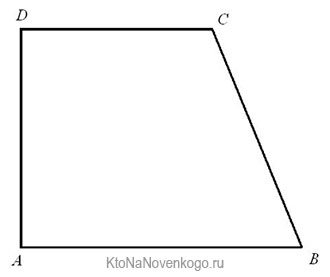
Прямоугольная трапеция – та, у которой одна из боковых сторон и основания образовывают прямой угол.
Выглядит она вот так:
В данном примере, углы DAB и ADC являются прямыми, то есть равны 90 градусам. А соответственно, трапеция называется прямоугольной.
Тут важно заметить, что под прямым углом к основанию должна идти только одна боковая сторона. Если будут обе, то трапеция автоматически превратится в квадрат.
Свойства трапеций
С трапециями связаны несколько понятий в геометрии, которые активно используются для решения различных теорем.
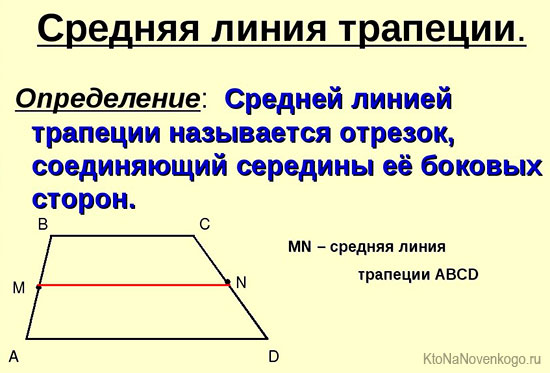
Средняя линия
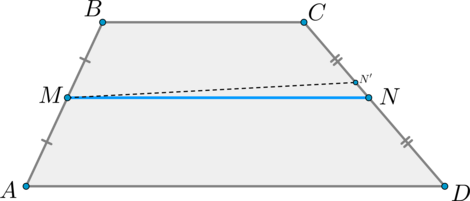
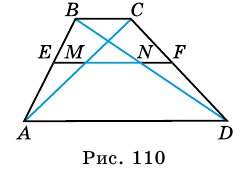
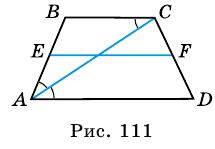
Средняя линия трапеции – это отрезок, который идет параллельно основаниям и соединяет середины:
Со средней линией связана одна интересная теорема. Очень часто на уроках геометрии школьников просят определить ее длину. И сделать это весьма просто.
Длина средней линии трапеции равна половине суммы длин ее оснований.
Звучит может и несколько тяжеловато. Но на деле – это весьма просто. Так, чтобы посчитать в нашем примере длину отрезка MN, который является средней линией, надо применить формулу:
И это правило распространяется на все виды трапеций.
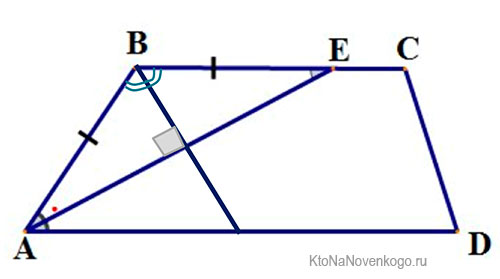
Биссектриса углов трапеции
Биссектриса – это линия (луч), которая делит угол пополам. Так вот
Любая биссектриса, выведенная из угла трапеции, отсекает на основании отрезок, равный по длине боковой стороне.
На данном рисунке отрезок АЕ является биссектрисой угла ABD. И исходя из этого, отрезки АВ и ВЕ равны между собой, о чем свидетельствуют небольшие черточки на них.
В то же время у биссектрис в трапеции есть еще одно свойство.
Две биссектрисы, выведенные из углов одной боковой стороны, пересекаются под прямым углом.
Все эти теоремы в процессе школьного обучения, ученикам еще необходимо доказывать. Ну а мы решили не приводить долгие математические и геометрические выкладки. Просто примите как данность!
Вот и все, что мы хотели рассказать вам о трапеции.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
А я, глядя на трапецию, пуделя своего вспомнил, о трапеции он ничего не знал, но вставал в такую стойку, что передние и задние лапы образовывали трапецию.
Что такое трапеция: определение, виды, свойства
В данной публикации мы рассмотрим определение, виды и свойства (касательно диагоналей, углов, средней линии, точки пересечения боковых сторон и т.д.) одной из основных геометрических фигур – трапеции.
Определение трапеции
Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.
Параллельные стороны называются основаниями трапеции (AD и BC), две другие стороны – боковыми (AB и CD).
Угол при основании трапеции – внутренний угол трапеции, образованный ее основанием и боковой стороной, например, α и β.
Трапеция записывается путем перечисления его вершин, чаще всего, это ABCD. А основаниям обозначаются маленькими латинскими буквами, например, a и b.
Средняя линия трапеции (MN) – отрезок, соединяющий середины ее боковых сторон.
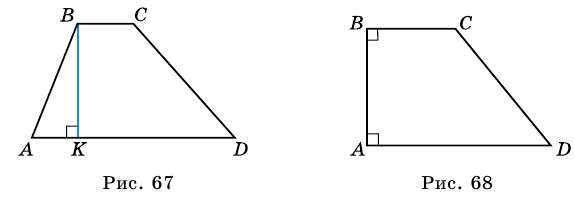
Высота трапеции (h или BK) – это перпендикуляр, проведенный от одного основания к другому.
Виды трапеций
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной (или равнобокой).
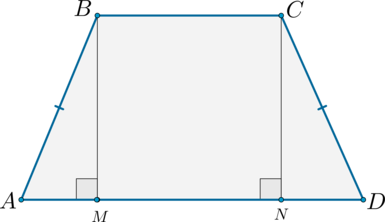
Прямоугольная трапеция
Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.
Разносторонняя трапеция
Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.
Свойства трапеции
Перечисленные ниже свойства применимы к любым видам трапеций. Свойства равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Свойство 1
Сумма углов трапеции, прилежащих к одной и той же боковой стороне, равна 180°.
Свойство 2
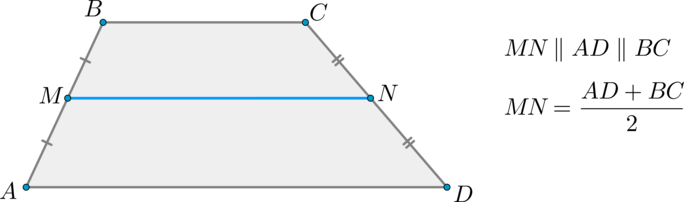
Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.
Свойство 3
Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.
Свойство 4
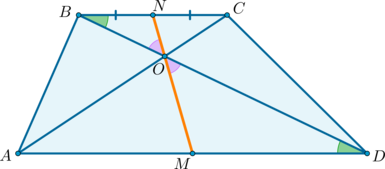
Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой.
Если сумма углов при одном основании равняется 90° (т.е. ∠DAB + ∠ADC = 90°), значит продолжения боковых сторон трапеции пересекаются под прямым углом, а отрезок, который соединяет середины оснований (ML) равняется половине их разности.
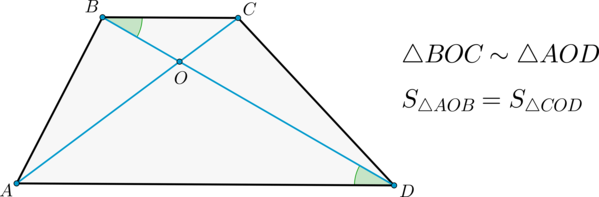
Свойство 5
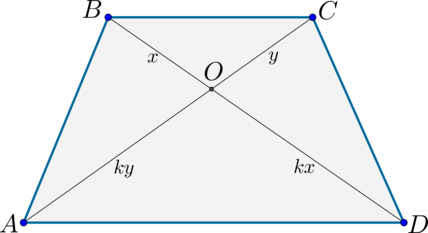
Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади.
Свойство 6
Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований:
Свойство 7
Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны.
Свойство 8
В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.
Т.е. AD + BC = AB + CD
Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.
Трапеция
Смотреть что такое «Трапеция» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Трапеции
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция | 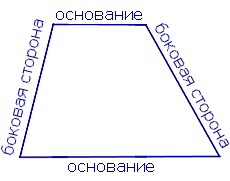 | |
| Определение | Диагонали трапеции | 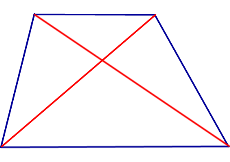 | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Определение | Высота трапеции | 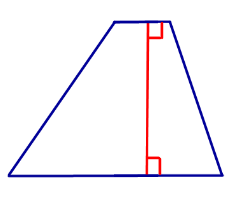 | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Свойство | Точка пересечения диагоналей | 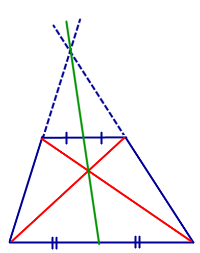 | |
| Определение | Средняя линия трапеции | 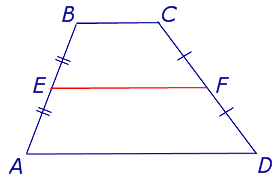 | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции |
| Свойство | |||
| Свойство | Биссектрисы углов при боковой стороне трапеции | 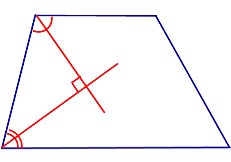 | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Определение: трапеция | |
 | |
| Определение: диагонали трапеции | |
 | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Определение: высота трапеции | |
 | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Свойство: точка пересечения диагоналей | |
 | |
| Определение: средняя линия трапеции | |
 | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции |
| Свойство: средняя линия трапеции | |
 | |
| Свойство: биссектрисы углов при боковой стороне трапеции | |
 | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
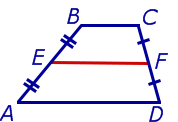
Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции

Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции

Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение

Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой
Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции
Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме

Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренная трапеция | 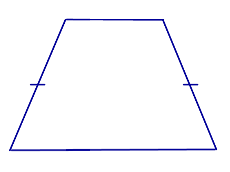 | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство | Равенство углов при основании | 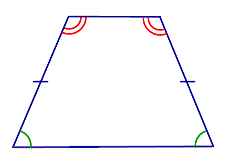 | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
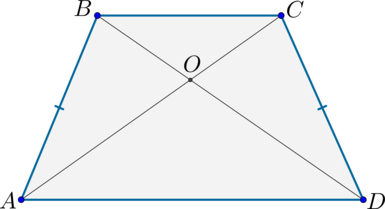
| Свойство | Равенство диагоналей | 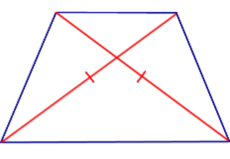 | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями | 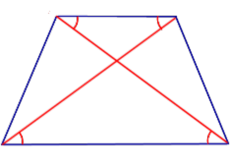 | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность | 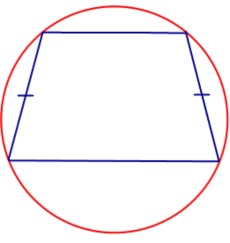 | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции | 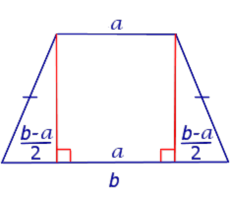 | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
 | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство: равенство углов при основании | |
 | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак: равенство углов при основании | |
 | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Свойство: равенство диагоналей | |
 | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак: равенство диагоналей | |
 | Если у трапеции диагонали равны, то она является равнобедренной |
| Свойство: углы, которые диагонали образуют с основаниями | |
 | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак: углы, которые диагонали образуют с основаниями | |
 | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Свойство: описанная окружность | |
 | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак: описанная окружность | |
 | Если около трапеции можно описать окружность, то она является равнобедренной. |
| Свойство: высоты трапеции | |
 | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Равнобедренная трапеция |
 |
Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны.

Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны.
Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной.

Свойство: Если трапеция является равнобедренной, то её диагонали равны.
Признак: Если у трапеции диагонали равны, то она является равнобедренной.

Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований.
Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной.

Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность.
Признак: Если около трапеции можно описать окружность, то она является равнобедренной.

Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований
Трапеция
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
Определение
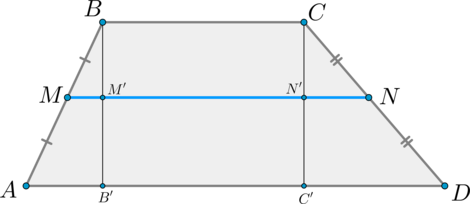
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
2) Докажем формулу.
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
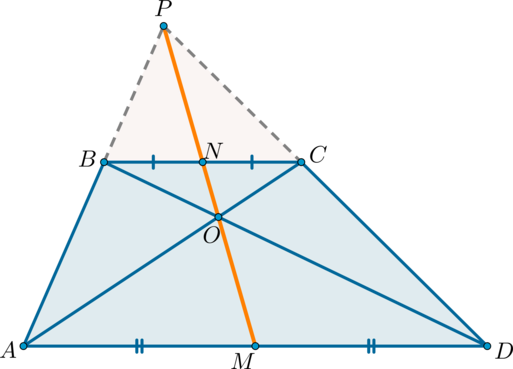
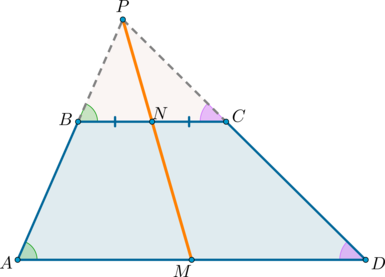
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
\(\triangle BNO\sim \triangle DMO\) по двум углам ( \(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
2)
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Что такое трапеция
Определение трапеции
Свойство трапеции
$\angle A+\angle B=180^<\circ>, \angle C+\angle D=180^<\circ>$ (рис 1)
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме:
Среди всех трапеций можно выбрать два особых класса трапеций: прямоугольные и равнобокие трапеции.
Прямоугольной называется трапеция, у которой один из углов прямой.
Равнобокой называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции
Признаки равнобокой трапеции
Примеры решения задач
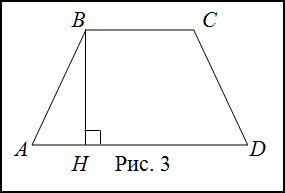
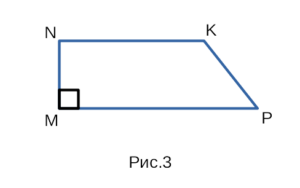
Задание. Высота равнобокой трапеции, проведенная из тупого угла, делит основание на отрезки длиной 5 см и 11 см. Найти периметр трапеции, если её высота равна 12 см.
Решение. Сделаем рисунок (рис. 3)
подставляя исходные данные, получим
$A B=\sqrt<144+25>=\sqrt <169>\Rightarrow A B=13$ (см)
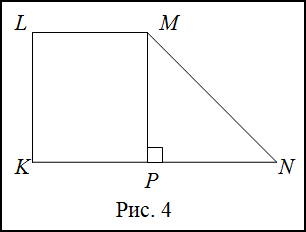
Решение. Сделаем рисунок (рис. 4)
$\angle N M P=180^<\circ>-\angle M P N-\angle M L K$
Значение слова «трапеция»
1. Четырехугольник с двумя параллельными сторонами.
[От греч. τραπέζιον]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
трапе́ция
1. геометр. четырёхугольник, у которого одна (в разных определениях — ровно одна, или минимум одна) пара противоположных сторон («основания трапеции») параллельна ◆ Площадь трапеции равна произведению полусуммы её основании на высоту.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: физиотерапевт — это что-то нейтральное, положительное или отрицательное?
ТРАПЕЦИЯ
Площадь Т. равна произведению средней линии на высоту Т. или половине произведения диагоналей на синус угла между ними. Т., боковые стороны к-рой равны между собой, наз. равнобочной.
Смотреть что такое «ТРАПЕЦИЯ» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
трапеция
Смотреть что такое «трапеция» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Трапеция
Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.
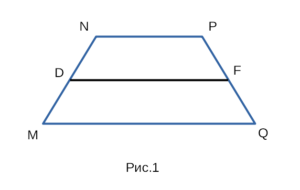
Элементы трапеции
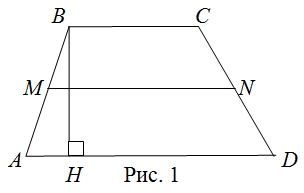
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.
В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.
Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.
Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.
Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.
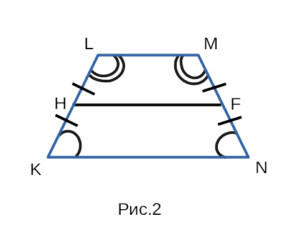
Виды трапеции
Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.
В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.
В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.
Определение трапеции
Из выпуклых четырехугольников, изучаемых в школьном курсе планиметрии, трапеция и параллелограмм — самые важные виды.
Запишем определение трапеции и рассмотрим ее основные элементы.
Трапеция — это четырехугольник, у которого две стороны параллельны, и две — не параллельны.
Параллельные стороны трапеции называются основаниями, не параллельные — боковыми сторонами.
Например, у трапеции ABCD, изображенной на рисунке 1, AD и BC — основания, AB и CD — боковые стороны.
Точки A, B, C, D — вершины трапеции.
Отрезки, соединяющие вершины трапеции, не принадлежащие одной стороне — это диагонали трапеции.

диагонали трапеции ABCD.

Чаще всего высоту трапеции проводят из вершины трапеции. Например, BF и CK — высоты трапеции ABCD.
Высоту трапеции можно провести из любой другой точки основания.
Например, PE — высота трапеции ABCD.
Поскольку расстояние между параллельными прямыми — это длина их общего перпендикуляра,
Трапеция и ее свойства с определением и примерами решения
Содержание:
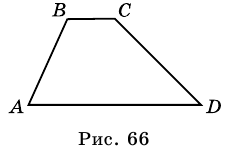
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 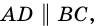
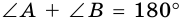
2. Трапеция является выпуклым четырехугольником.
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 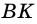
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 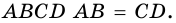
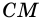
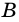
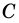
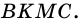
2) 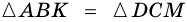
3) Также 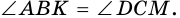
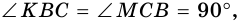
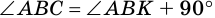
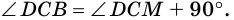
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 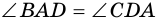
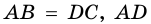
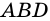
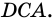
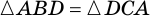
Пример:
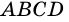
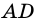
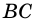
Доказательство:
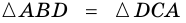
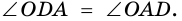
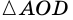
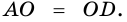
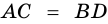
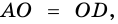
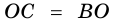
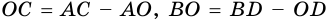
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 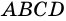
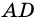
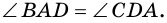
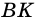
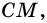
2) Тогда 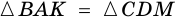
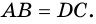
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 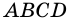
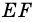
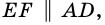
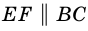
1) Проведем луч 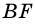
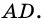
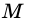
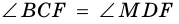
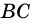
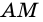
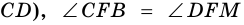
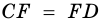
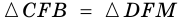
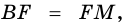
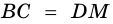
2) Поскольку 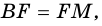
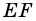
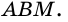
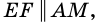
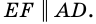
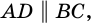
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 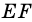
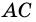
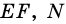
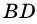
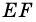
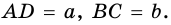
1) Так как 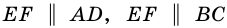
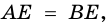
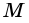
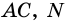
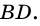
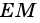
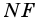
Тогда
2) 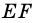
3)
Пример:
Решение:
Пусть 
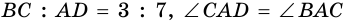
1) Обозначим 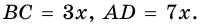
2) 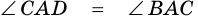
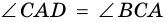
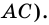
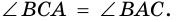
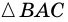
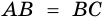
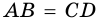
3) Учитывая, что 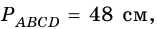
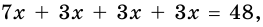
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Геометрия
План урока:
Трапеция
Рассмотрим четырехуг-к, у которого параллельны только две стороны, а две оставшиеся не параллельны. Такая фигура именуется трапецией.
На рисунке трапеция выглядит следующим образом:
Параллельные стороны именуются основаниями трапеции, а другие две – это боковые стороны.
Обратите особое внимание на то, что одно из оснований всегда больше второго основания. Действительно, если бы основания имели одинаковую длину, то получился бы четырехуг-к, у которого две противоположные стороны и равны, и параллельны. Однако это уже один из признаков параллелограмма, а параллелограмм никак не может быть трапецией.
Иногда полезно представлять трапецию как усеченный треуг-к. Действительно, если в треугольнике провести линию, параллельную одной из сторон и пересекающую две остальные стороны, то она как бы «отсечет» верхушку этого треуг-ка, и получится трапеция. И наоборот, любую заданную трапецию можно достроить до треугольника:
Сумма всех 4 углов трапеции составляет, как и у любого четырехугольника, 360°.
Задание. Известно, что у трапеции АВСD АD||ВС, ∠А = 36°, ∠С = 117°. Найдите∠В и ∠D.
Решение: АВ можно рассматривать как секущую параллельных прямых ВС и АD. Но тогда∠А и ∠В будут являться односторонними, а их сумма будет равна 180°. Отсюда можно найти ∠В:
Аналогично, рассматривая в качестве секущей СD, можно найти и ∠D, который вместе с∠С является односторонним:
Средняя линия трапеции
Если отметить середину каждой из боковых сторон трапеции, а потом соединить эти середины, то получится отрезок, именуемый средней линией трапеции.
Докажем важную теорему, связанную со средней линией:
Для этого изучим трапецию АВСD, у которой боковые стороны – это АВ и CD. Пусть М – середина АВ. Проведем через М прямую, параллельную основаниям, которая пересечет СD в точке N. По теореме Фалеса параллельные друг другу прямые АD, МN и ВС отсекут на прямой СD равные отрезки, то есть СN = ND. Но это означает, что N– середина CD, а тогда MN – средняя линия (согласно ее определению). Естественно, что в трапеции возможно построить только одну среднюю линию, а значит, средняя линия МN параллельна каждому из оснований.
Прямоугольная и равнобедренная трапеция
Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.
Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия
Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?
Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:
Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:
Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.
Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.
Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.
В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда
Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.
Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь
Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:
Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:
Несколько сложнее доказать другую теорему:
Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:
Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что
Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,
Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.
Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:
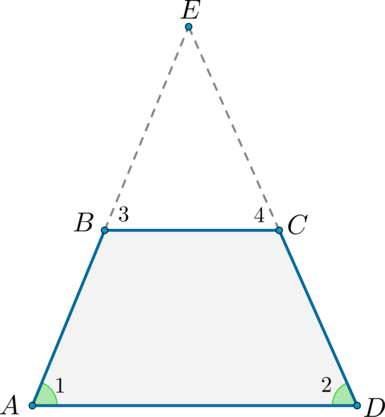
Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:
Действительно, если АВСD – равнобедренная трапеция, то
Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.
Прямоугольник
Следующим особым четырехугольником является прямоугольник (иногда его сокращенно обозначают как прямоуг-к). Его отличительный признак заключается в том, что все его углы – прямые.
Продемонстрируем несколько прямоугольников:
Очевидно, что у прямоуг-ка противоположные стороны параллельны, ведь они перпендикулярны одной и той же прямой. Следовательно, всякий прямоуг-к одновременно является параллелограммом и обладает всеми его свойствами. Стоит особо отметить, что обратное утверждение неверно – отнюдь не всякий параллелограмм является прямоугольником. Другими словами, прямоугольник – это частный случай параллелограмма, который отличается тем, что его углы составляют 90°.
Из этого вытекает два свойства прямоугольника:
Однако есть ещё одно свойство, которое НЕ характерно для остальных параллелограммов.
Доказать это очень просто. Пусть есть прямоугольник АВCD:
Сравним ∆АВD и ∆АСD. Они являются прямоугольными, у них есть общий катет АD, а два других катете, АВ и СD, равны как противоположные стороны прямоугольника. Получается, что рассматриваемые треуг-ники равны, и поэтому равны и их гипотенузы, которые как раз и являются диагоналями прямоугольника.
Оказывается, верна и обратная теорема, которую называют признаком прямоугольника:
Действительно, пусть есть некоторый параллелограмм АВCD, у которого одинаковы диагонали АС и BD.
Противоположные стороны в одном параллелограмме одинаковы:
В итоге все углы АВСD оказываются прямыми, и эта фигура по определению оказывается прямоуг-ком.
Задание. В прямоуг-ке ABCD проведена биссектриса, которая делит сторону СD на отрезки СК и КD длиной 27 и 45 см соответственно. Найдите периметр АВCD.
Решение.Для нахождения периметра необходимо найти длины всех сторон.
Если АК – биссектриса, то
∆КАD является прямоугольным, и мы только что нашли один из его острых углов. Тогда можно найти и 2-ой угол:
Получается, что в ∆АКD два угла равны 45°, значит, он является равнобедренным, и
Мы нашли две смежные стороны прямоугольника, АD и СD. Две другие стороны будут им равны:
Следующая особенная фигура – это ромб. Дадим определение ромба:
На рисунке видно, что ромб похож на параллелограмм, и это не случайно. Докажем, что любой ромб является частным случаем параллелограмма. Но прежде заметим, что обратное утверждение неверно – отнюдь не каждый параллелограмм является ромбом.
Для доказательства этого факта проведем диагональ ромба:
В результате получилось два треуг-ка: ∆АВС и ∆АСD. Можно заметить два факта. Во-первых, каждый из этих треуг-ков – равнобедренный, ведь стороны ромба равны. Тогда можно записать равенство углов:
Из равенства треуг-ков вытекает и равенство углов:
Тогда очевидно, что ∠А и ∠С также равны, ведь они состоят из двух равных углов:
В итоге получается, что в ромбе противоположные углы одинаковы. Зная, что все 4 угла в сумме дают 360°, легко найдем сумму каких-нибудь двух смежных углов:
Итак, сумма смежных углов в ромбе равна 180°. Но эти углы можно рассматривать как односторонние. Если их сумма равна 180°, то и соответствующие прямые (в частности, ВС и АD) параллельны. Аналогично доказывается и то, что АВ||CD. Это и значит, что АВСD– параллелограмм.
Продолжим рассматривать построенный нами рисунок, но добавим в него ещё одну диагональ:
Во-первых, мы уже доказали следующее равенство
Из него вытекает, что диагональ АС является биссектрисой для∠А и ∠С. Аналогично и для диагонали ВD можно показать, что и она разбивает ∠В и ∠D пополам. Можно сформулировать следующее свойство ромба:
Далее рассмотрим ∆АВD. Он равнобедренный, а АО является биссектрисой, падающей на основание ВD. Но в равнобедренном треуг-ке такая биссектриса одновременно является высотой, то есть
Получается, что диагонали всякого ромба обязательно пересекаются под прямым углом.
Задание. Длина стороны ромба совпадает с длиной одной из его диагоналей. Определите углы этого ромба.
Решение. Построим рисунок по условию задачи:
Легко заметить, что∆АВС и ∆АСD будут равносторонними. Однако все углы равностороннего треуг-ка равны 60°:
Итак, два угла ромба будут равны 60°, а другие два 120°.
Квадрат
Последний особый случай четырехугольника – это квадрат. Эта фигура, которая сразу является и прямоугольником, и ромбом. Естественно, что любой квадрат одновременно является параллелограммом. Дадим определение квадрата:
Свойства квадрата – это совокупность свойств параллелограмма, ромба и прямоуг-ка.Это значит, что его диагонали:
Задание. Середины сторон квадрата соединили отрезками. Докажите, что получившаяся фигура также является квадратом.
Решение. Требуется доказать, что фигура, показанная красным цветом, является квадратом:
Так как стороны квадрата одинаковы, то одинаковы и их половины:
Получается, что ∆АМН, ∆МВР, ∆РСК и ∆КНD – прямоугольные, причем у них равны все катеты. Это значит, что, с одной стороны, они являются равнобедренными треуг-ками, а с другой стороны, они равны друг другу. Мы уже знаем, что у равнобедренного прямоугольного треуг-ка углы при основании составляют по 45°, а из равенства треуг-ков вытекает, что
Получается, что у четырехуг-ка МРКН все стороны одинаковы, то есть он является ромбом. Осталось доказать, что все его углы прямые. Рассмотрим, например, ∠РМН. Он в сумме с ∠ВМР и ∠АМН дает 180°, что позволяет вычислить его:
Итак, все углы ромба МРКН прямые, значит, он является квадратом.
Мы видим, что есть множество видов четырехугольников, причем часто одна и та же фигура может относиться сразу к нескольким типам. Для наглядности покажем на одной картинке всю иерархию четырехугольников. Здесь на одном рисунке можно увидеть название всех видов четырехугольников, их форму, также главное свойство, по которым их и определяют:
Симметрия
В заключение рассмотрим также такое важное геометрическое понятие, как симметрия.
В случае, показанном на рисунке,А1 и А2 не лежат на b. Если же рассматривается точка, лежащая на b, то она считается симметричной самой себе. На рисунке пары точек А и B, C и D, M и N симметричны относительно b.Для точки же Р нельзя найти парную ей симметричную точку. Поэтому условно считается, что она симметрична сама себе.
Теперь перейдем к такому понятию, как симметричная фигура.
В качестве иллюстрации приведем равнобедренный треуг-к. У него роль оси симметрии играет медиана, проведенная к основанию. Выберем на треугольнике произвольные точки А1, В1, С1 и D1. Далее отметим симметричные им относительно b точки, которые обозначим как А2, В2, С2 и D2. Видно, что они также принадлежат треугольнику:
Рассмотрим для иллюстрации и какую-нибудь несимметричную фигуру, например, треугольник с 3 разными сторонами:
Видно, что например, для точка А1 симметричная ей А2 НЕ принадлежит треугольнику, поэтому красная линия НЕ является осью симметрии.
Осевая симметрия присуща и многим другим фигурам:
Обратите внимание, что осей симметрии фигуры может быть несколько. У ромба их две (это его диагонали), у квадрата уже четыре (помимо диагоналей добавляются ещё и линии, соединяющие середины его противоположных сторон), а у окружности их и вовсе бесконечно много, так как любой ее диаметр может играть эту роль.
Возможен ещё один случай симметрии:
На приведенном рисунке С – это середина АВ, поэтому А и В симметричны, а точка С для них является центром симметрии.
Снова перейдем от отдельных точек к фигурам.
В частности, центральная симметрия присуща параллелограмму (его центром симметрии будет точка, в которой пересекаются его диагонали), а также окружность. Есть центральная симметрия и у любой прямой, причем в качестве центра симметрии фигуры можно выбрать любую точку, принадлежащую этой прямой:
Симметрия – это не просто умозрительная геометрическая конструкция, она встречается и в реальной жизни. Например, листья многих деревьев обладают осевой симметрией, а зубчатое колесо – центральной симметрией. Интересно, что из 32 выделяемых в царстве животных типов у представителей 28 (это более 99% известных видов) можно выделить правую и левую половину, которые симметричны друг другу. Архитекторы и конструктора при проектировании зданий и машин стремятся придать им симметричную форму, так как в большинстве случаев именно такая форма оказывается оптимальной и экономичной.
Трапеция
Смотреть что такое «Трапеция» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
ТРАПЕЦИЯ
Полезное
Смотреть что такое «ТРАПЕЦИЯ» в других словарях:
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
ТРАПЕЦИЯ
Смотреть что такое «ТРАПЕЦИЯ» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
ТРАПЕЦИЯ
Смотреть что такое «ТРАПЕЦИЯ» в других словарях:
ТРАПЕЦИЯ — (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция — Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
ТРАПЕЦИЯ — (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ — (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ — ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ — жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ — (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция — четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Что такое трапеция: свойства четырёхугольника, теоремы и формулы

Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
Кроме того, часто полезно знать и применять следующие утверждения:
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.
Вписанная и описанная окружность
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
ТРАПЕЦИЯ И ЕЕ СВОЙСТВА
С.И. Ожегов определяет это понятие как четырехугольник с двумя параллельными и двумя непараллельными сторонами.
Понятие трапеции развивается в планиметрии как отдельная фигура, в стереометрии как грань усеченного геометрического тела, в высшей математике можно рассчитать площадь криволинейной трапеции. Это действие происходит путем вычисления определенного интеграла. Определенным интегралом называют конечный предел суммы в промежутке от до [15]:
Задачи на трапецию в повседневной жизни используются многими. Изучение свойств трапеции необходимо, так как они применяются в живописи, быту, строительстве, архитектуре, технике. Также задачи на данную фигуру встречаются в ОГЭ в 9 классе и далее в ЕГЭ в 11 классе. В 9 задании ОГЭ четверть заданий посвящена решению задач на свойства трапеции. В ЕГЭ различные задачи на трапецию встречаются в 5-6 заданиях. Отсюда и возникает потребность в изучении школьниками свойств трапеции.
Изучению понятия трапеции, ее свойств и приложений к решению задач посвящена данная работа по теме «Трапеция и ее свойства».
Объект исследования: геометрические фигуры.
Предмет исследования: методы и приемы решения задач по теме «Трапеция и ее свойства».
Цель исследования: систематизация теоретического материала по теме «Трапеция и ее свойства» и его применение к решению задач.
Курсовая работа состоит из введения, двух глав, заключения и списка литературы. Список использованной литературы включает 19 наименований.
Результаты курсовой работы были апробированы на IV внутривузовской студенческой научно-практической конференция «Молодежь в мире науки» в СурГПУ и на XXI студенческой научно-практической конференции «Студенчество в научном поиске» в СурГПУ.
I. Теоретическая часть
Планиметрия изучает фигуры и их свойства на плоскости. Рассматриваемая нами фигура трапеция относится к данному разделу. В учебниках и учебных пособиях разных авторов трактуется определение трапеции практически одинаково, т.е. это четырехугольник, у которого две стороны параллельны, а две другие нет (, рис. 1) [2], [12], [16]. Однако М.Я. Выгодский утверждает, что параллелограмм можно считать частным случаем трапеции [2]. Треугольник является предельным случаем («вырождением») трапеции, когда одно из оснований обращается в точку. В вырожденной трапеции сохраняются ее свойства.
Рассмотрим основные понятия, связанные с трапецией.
Существует следующая классификация трапеций:
равнобокая (равнобедренная), боковые стороны которой равны;
прямоугольная, у которой один угол прямой.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции ( на рис. 1). Средняя линия делит высоту трапеции пополам.
Теорема 1.Средняя линия трапеции параллельна основаниям и равна их полусумме:
Отсюда и вытекает следствие 1, что прямая, проходящая через середину боковой стороны трапеции, параллельная основаниям, делит вторую боковую сторону пополам.
Существует свойство, что углы при основании равнобедренной трапеции равны.
Из этой теоремы вытекает ряд следствий:
сумма противоположных углов равнобедренной трапеции равна 180;
в равнобедренной трапеции диагонали равны;
перпендикуляр, восставленный из середины одного из оснований равнобедренной трапеции, является ее осью симметрии и, следовательно, делит пополам другое основание.
Формулы для вычисления площади трапеции.
Следствие 5. Площадь трапеции равна произведению средней линии на высоту. Это следует из того, что средняя линия трапеции равна полусумме ее оснований.
Рассмотрим дополнительные формулы для вычисления площади трапеции :
Воспользовавшись теоремой Пифагора, составим следующую систему уравнений и решим ее, выразив при этом :
2) В равнобедренной трапеции с перпендикулярными диагоналями высота равна средней линии трапеции и площадь такой трапеции равна квадрату средней линии:
3) Также, для трапеции подходит универсальная формула нахождения площади четырехугольника через ее диагонали:
4) Следующая формула нахождения площади трапеции будет связана с параллелограммом Вариньона, и она звучит так: площадь трапеции равна удвоенной площади параллелограмма Вариньона.
В трапеции существуют средние величины. Средняя линия трапеции является средним арифметическим оснований. В элементраной метаматематике используются среднее геометрическое и среднее гармоническое оснований, которые величины представляют определенный интерес при решении геометрических задач.
Рассмотрим задачи на использование этих величин.
Средним геометрическим двух оснований трапеции будет являться:
Общее основание двух подобных трапеций.Если трапеции с общим основанием подобны, то их общее основание является средним геометрическим двух других оснований трапеции.
2) Высота равнобедренной трапеции, описанной около окружности.
Среднее гармоническое двух оснований трапеции является значение выражения и в трапеции оно выражается следующим образом:
Высота прямоугольной трапеции, описанной около окружности, равна среднему гармоническому оснований.
2) Отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей, равен среднему гармоническому оснований.
Используя результаты равенства (1), получим:
Рассмотрим связь между трапецией и окружностью. Окружность может быть либо вписанная в трапецию, либо быть описанной. Однако не около любой трапеции можно описать окружность. Окружность описать можно только лишь около равнобедренной трапеции, так как сумма противоположных углов четырехугольника составляет 180 [2]. Отсюда вытекает следствие 6, что если около трапеции можно описать окружность, то она является равнобедренной.
Трапеция вписанная. Радиус описанной около трапеции окружности можно найти из следствия теоремы синусов. Из треугольника (рис. 11) имеем:
Теорема 2 (Птолемея). Произведение диагоналей равно сумме произведений противоположных сторон (рис. 11):
Трапеция описанная. В трапецию можно вписать окружность, только тогда, когда сумма противоположных сторон будет равна (по свойству вписанной окружности в четырехугольник):
Также, боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.
Теорема 3. В трапеции проведена прямая параллельно основаниям. Если в образовавшиеся трапеции можно вписать окружности, то трапеции подобны.
Из подобия треугольников и : (4)
В данной главе мы рассмотрели основные теоретические положения по теме «Трапеция и ее свойства». Дано определение трапеции, установлено, что данная геометрическая фигура разделяется на 3 вида: произвольная, равнобедренная и прямоугольная. Мы вывели формулы, связанные с вычислением основных элементов в трапеции любого вида. Также рассматривался вопрос вычисления площадей через стороны трапеции, через квадрат среднего арифметического двух оснований равнобедренной трапеции, универсальную формулу для вычисления площади четырехугольника с помощью диагоналей и через площадь параллелограмма Вариньона.
Рассмотрению методов решения геометрических задач по данной теме будет посвящена практическая часть курсовой работы.
II. Практическая часть
В теоретической части курсовой работы были представлены основные теоретические сведения, которые нам понадобятся в решении геометрических задач.
Рассмотрим методы решения геометрических задач, с помощью которых можно решать задачи на тему «Трапеция и ее свойства».
Для того чтобы можно было легко решить задачу на «трапецию», обычно разбивают трапецию на более простые геометрические фигуры – треугольники.
Метод дополнительного построения. Всякое решение геометрической задачи начинается с выполнения чертежа. Но иногда не всегда можно увидеть связи между данными величинами, а если достроить фигуру, то эти связи становятся очевидными.
Выделяют большое множество дополнительных построений, но в нашей работе мы будем пользоваться следующими дополнительными построениями:
опускание высот из концов одного основания на другое;
проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину;
проведение через середину меньшего основания прямых, параллельных боковых сторонам;
продолжение боковых сторон трапеции до пересечения;
проведение через одну из вершин трапеции прямой, параллельной диагонали.
Дополнительные построения чаще всего используются для того, чтобы свести задачу к ранее решенной задаче или более простой задаче.
Составим систему уравнений:
Особенностью трапеции является наличие пары параллельных сторон. При их пересечении любой прямой образуются равные углы, что приводит к появлению пар подобных треугольников, и соответственно, пропорциональных отрезков. В соответствии с теоремой Фалеса пропорциональные отрезки возникают на боковых сторонах трапеции или их продолжениях, если проводится прямая, параллельная основаниям.
При решении задач на подобие используются:
признаки подобия треугольников;
свойство средней линии трапеции;
теорема Пифагора и обратная ей.
Задача 3. Диагонали прямоугольной трапеции взаимно перпендикулярны, и большая из них точкой пересечения делится на отрезки, равные 36 и 64. Найдите основания трапеции.
Рассмотрим и : (как вертикальные углы), (как накрест лежащие при и секущей ).
Следовательно, по первому признаку подобия треугольников.
Найти: косинус меньшего угла.
Метод введения вспомогательного неизвестного. Данный метод предполагает введение новой неизвестной переменной, с помощью которой составляется уравнение или система уравнений. В качестве вспомогательных аргументов обычно выбирают величины, которые вместе с данными из условия задачи дают набор элементов, однозначно задающих некоторые фигуры.
Задача 5. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции.
Воспользуемся формулой для вычисления площади трапеции:
Составим систему уравнений:
Метод площадей. Главным объектом данного множества является площадь. Для треугольника площадь довольно просто выражается через разнообразные комбинации элементов треугольника. Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данных фигур. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое можно определить неизвестное.
Задача 6. Трапеция разделена диагоналями на 4 треугольника. Определить ее площадь, если площади треугольников, прилежащих к основаниям, равны 36 и 49.
Подставим значения и и получим:
Также, не исключено, что в задачах может встречаться комбинация методов решения, так как не всегда можно решить задачу, воспользовавшись только одним методом.
В данной главе мы рассмотрели методы решения задач на тему «Трапеция и ее свойства» и решили задачи, пользуясь ими. Мы выделили 4 метода: метод дополнительного построения, метод подобия, метод введения нового переменного и метод площадей. Выбор метода решения задачи исходит из того, какие данные нам будут известны, и какие нужно найти. В задаче может использоваться один и более методов, в зависимости от сложности.
В данной работе изложены вопросы, касающиеся понятия трапеции и ее свойств. В процессе анализа математической литературы, посвященной теме курсовой работы, мы выделили следующие теоретические положения, которые представлены в первой главе:
Основные понятия, связанные с трапецией, и ее свойства;
Формулы для вычисления площади;
Средние величины в трапеции;
Вписанная окружность в трапецию;
Описанная окружность около трапеции.
Мы установили, что трапецией является четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Далее, мы выделили методы решения задач по теме нашей работы и решили планиметрические задачи, пользуясь данными методами:
Введения вспомогательного неизвестного;
Каждый метод имеет свои особенности, которые мы также изложили во второй главе нашей курсовой работы.
Таким образом, цель нашего исследования была достигнута.
Приведенная типология задач по методам решения, описанные в работе, могут быть использованы в разработке методических рекомендаций к проведению факультативных занятий по математике в курсе средней общеобразовательной школы, а также при подготовке учащихся к государственным экзаменам.
Список используемой литературы
Атанасян, Л.С. Геометрия. 7-9 классы [Текст] : учебник для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 2-е изд. – М. : Просвещение, 2014. – 383 с.
Выгодский, М.Я. Справочник по элементарной математике [Текст] : справочник / М.Я. Выгодский. – М. : АСТ : Астрель, 2015. – 509 с.
Глаголев, Н.А. Элементарная геометрия [Текст] : уч. пособие для учащихся 6-8 классов / Н.А. Глаголев, под ред. Д.И. Перепелкина. – М. : Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1954. – 235 с.
Глейзер, Г.И. История математики в школе [Электронный ресурс] : пособие для учителей / Г.И. Глейзер, под ред. В.Н. Молодшего. – М., 1964. – 376 с.
Готман, Э.Г. Задачи по планиметрии и методы их решения [Текст] : пособие для учащихся. – М. : Просвещение: АО «Учеб. лит.», 1996. – 240 с.
Евклид, Начала Книги I-IV. – М. : ГТТИ, 1948 – 1950.
Зеленяк, О.П. Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Моделирование в среде Turbo Pascal [Текст] : уч. пособие / О.П. Зеленяк. – Киев, Москва : ДиаСофтЮП, ДМК Пресс, 2008 – 336 с.
Кушнир, И.А. Избранные задачи по геометрии. Трапеция [Текст] / И.А. Кушнир. – М. : ИЛЕКСА, 2016. – 96 с.
Ожегов, С.И. Толковый словарь русского языка / С.И. Ожегов, Н.Ю. Шведова. – М.: ИТИ Технологии, 4-е изд., 2013. – 944 с.
Погорелов, А.В. Геометрия. 7-9 классы [Текст] : учебник для общеобразоват. организаций / А.В. Погорелов. – 2-е изд. – М. : Просвещение, 2014. – 240 с.
Прасолов, В.В. Задачи по планиметрии [Текст] : учеб. пособие. – 5 изд. – М. : МЦНМО: ОАО «Московские учебники», 2006. – 640 с.
Смирнова, И.М. Геометрия. 7-9 классы [Текст] : учебник для общеобразоват. организаций / И.М. Смирнова, В.А. Смирнов. – 9 изд. – М. : Мнемозина, 2015. – 376 с.
Сурина, О.П. Элементарная геометрия [Текст] : уч. пособие для студентов направления подготовки Педагогическое образование профилей «Математика», «Физика», «Информатика». – Пенза: издательство ПГУ, 2012. – 107 с.
Фильчаков, П.Ф. Справочник по элементарной математике [Текст] : уч. пособие / П.Ф. Фильчаков. – Киев. : Наукова Думка, 1972. – 528 с.
Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления [Текст] : уч. пособие / Г.М. Фихтенгольц. – 2 том. – М. : ФИЗМАТЛИТ, 2006. – 800 с.
Цыпкин, А.Г. Справочник по математике [Текст] : справочник для ср. уч. заведений. – 3 изд. – М. : Наука. Главная редакция физико-математической литературы, 1983. – 480 с.
Ященко, И.В. ЕГЭ 2017. Математика. Профильный уровень. Типовые тестовые задания [Текст] / И.В. Ященко, М.А. Волчеквич, И.Р. Высоцкий, Р.К. Гордин и др. – М. : Издательство «Экзамен», 2017. – 55 [1] с.
Ященко, И.В. Математика. Профильный уровень. 20 вариантов тестов. Тематическая рабочая тетрадь [Текст] / И.В. Ященко, С.А. Шестаков, А.С. Трепалин, П.И. Захаров. – М. : Издательство «Экзамен», МЦНМО, 2017. – 295 [1] с.
Ященко, И.В. ОГЭ. Математика : типовые экзаменационные варианты : 36 вариантов [Текст] / под ред. И.В. Ященко. – М. : Издательство «Национальное образование», 2016. – 240 с.