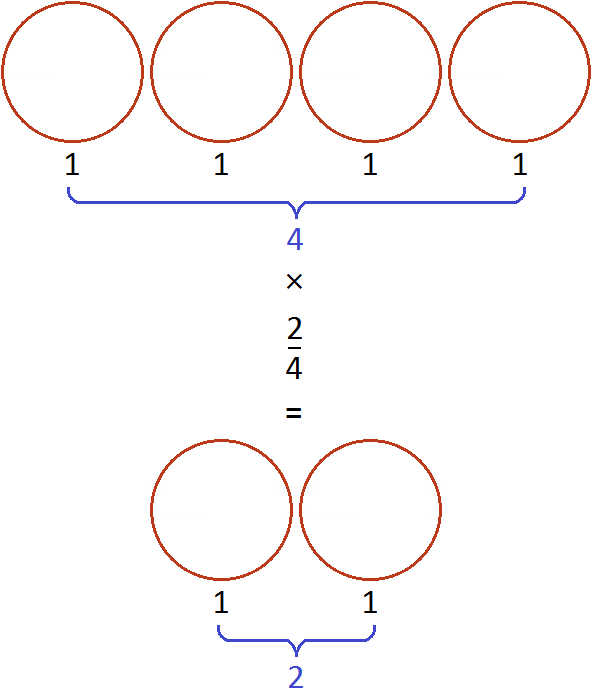
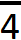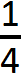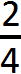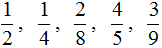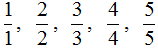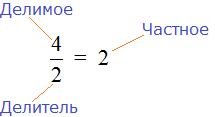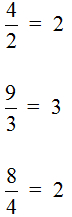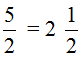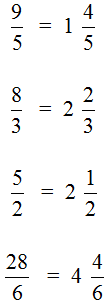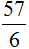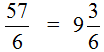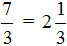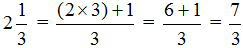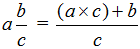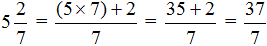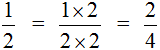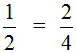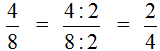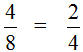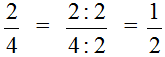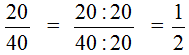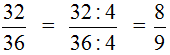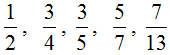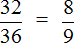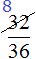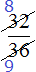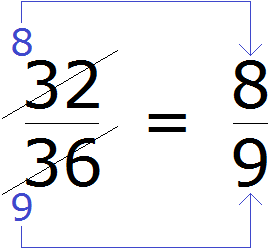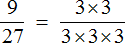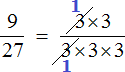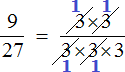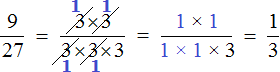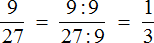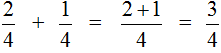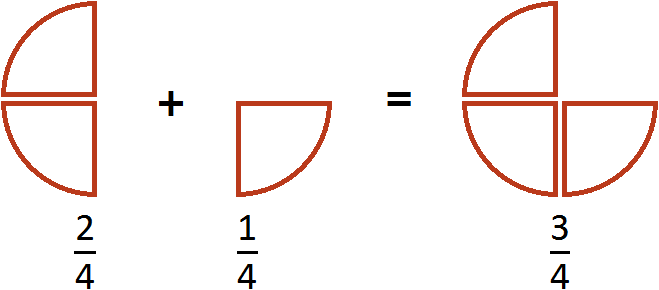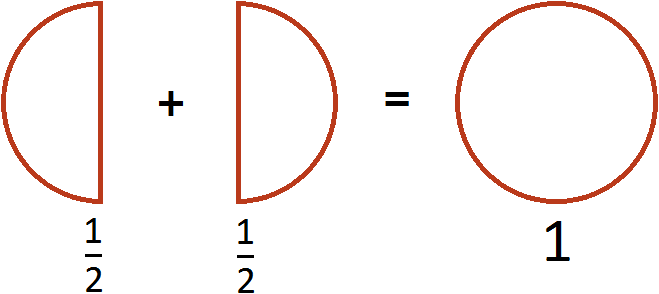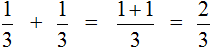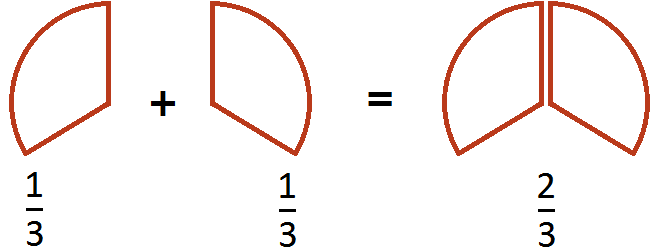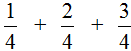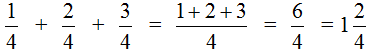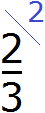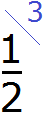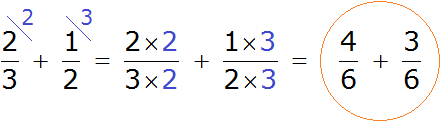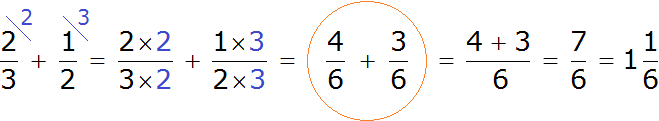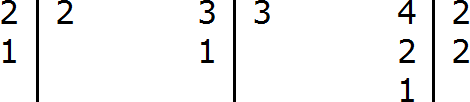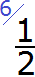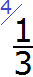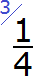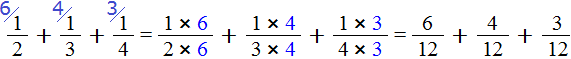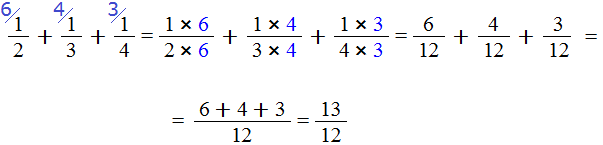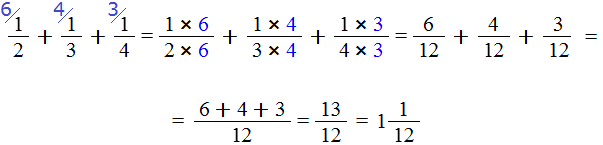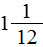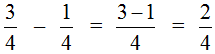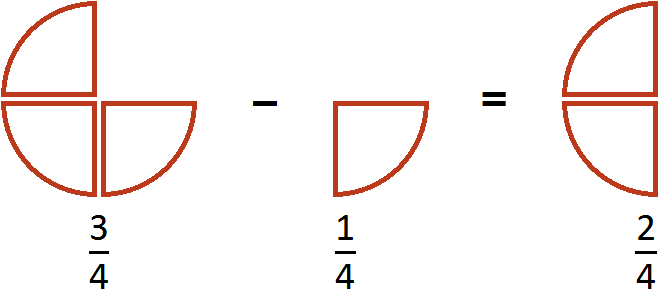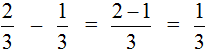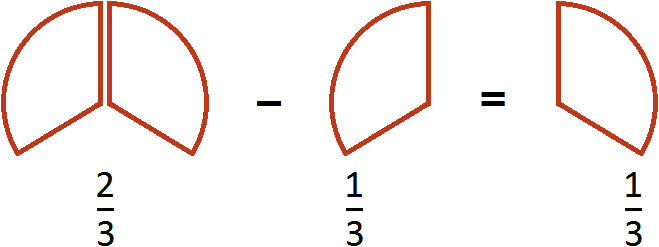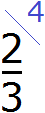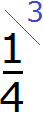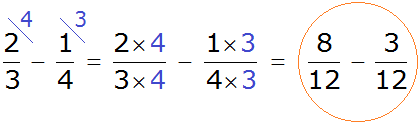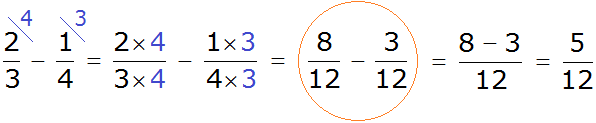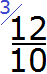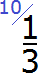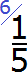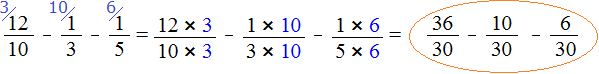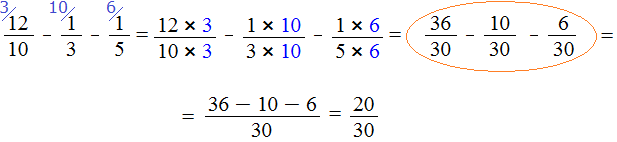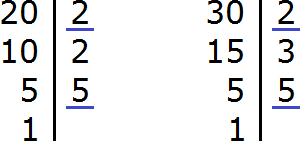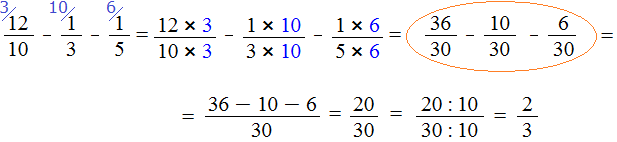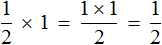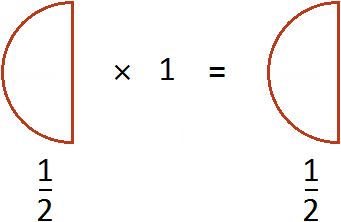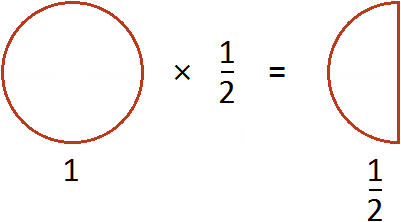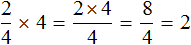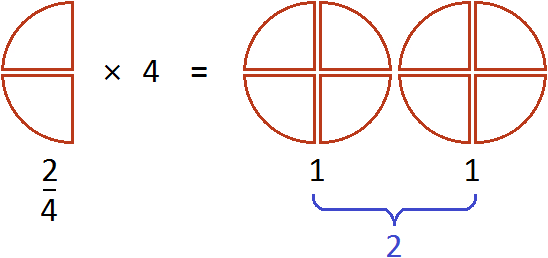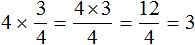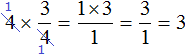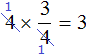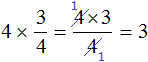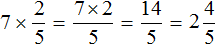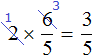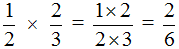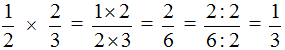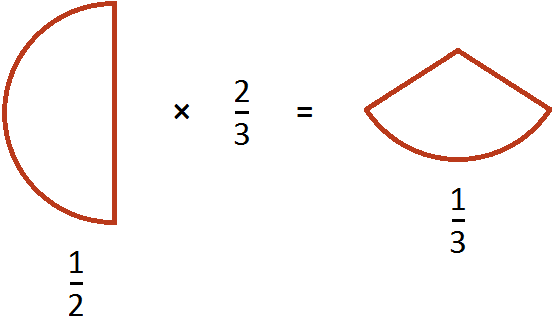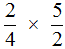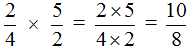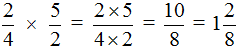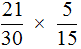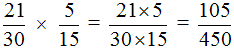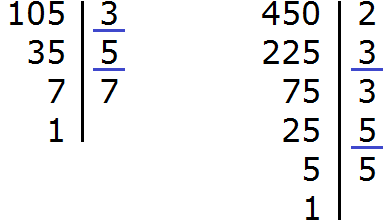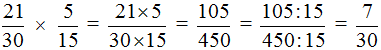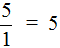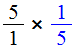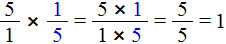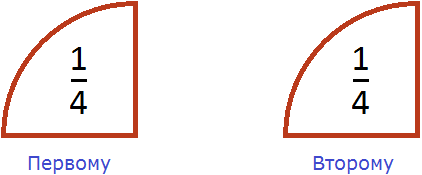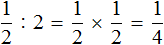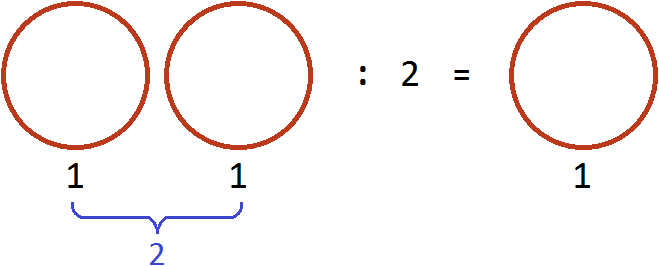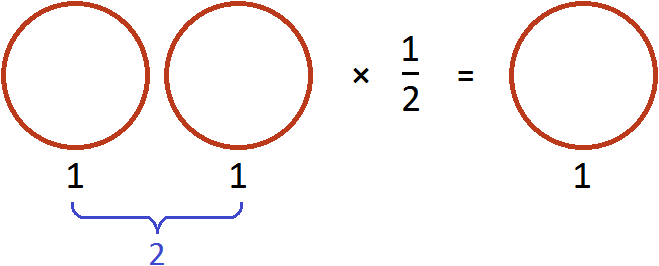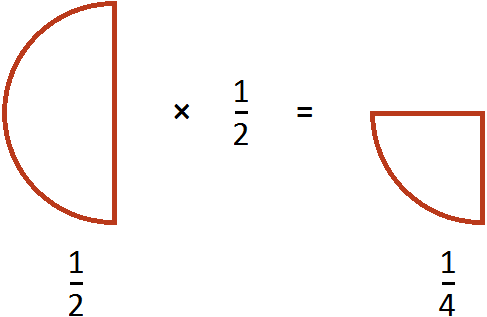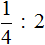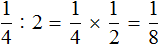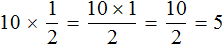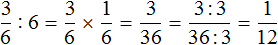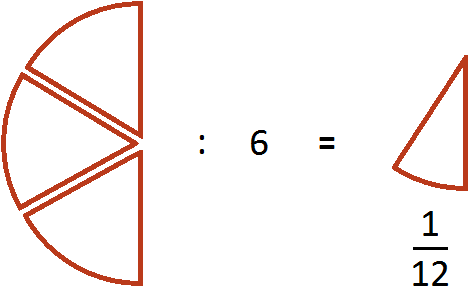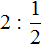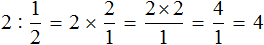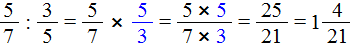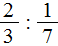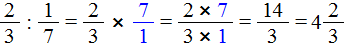Дроби как считать

Как решать дроби. Решение дробей.

В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!

Понятие дроби вводится в курс математики начиная с 6 класса средней школы.

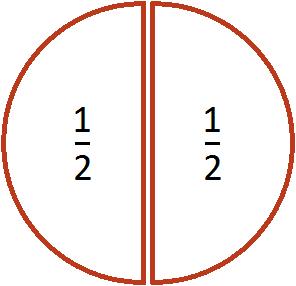
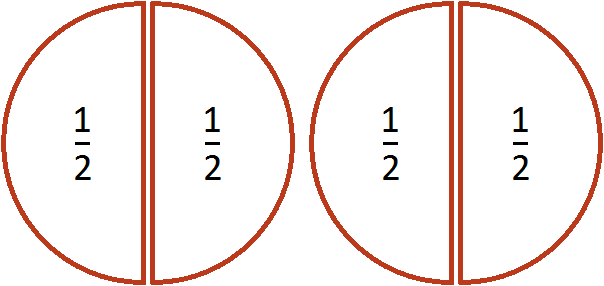
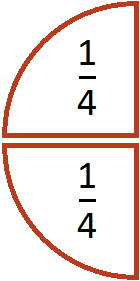
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.

Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.

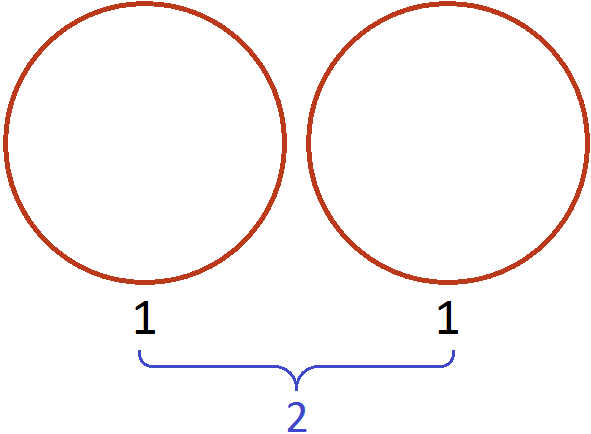
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.

Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.

Например, 5 целых 3/4.

Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.

Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.

Как решать дроби. Примеры.

К дробям применимы самые разные арифметические операции.

Приведение дроби к общему знаменателю

Например, необходимо сравнить дроби 3/4 и 4/5.

Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей

Наименьший общий знаменатель(4,5) = 20

Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю

Источник

Калькулятор дробей

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d

5 3 4 = 5 · 4 + 3 4 = 23 4

Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную или смешанную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

Например, переведем 0.36 в обыкновенную дробь:

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

Умножение дробей

Алгоритм действий при умножении двух дробей:

Деление дробей

Алгоритм действий при делении двух дробей:

Источник

Обыкновенные дроби

Доля целого

Доля это каждая из равных частей, на которые поделено целое.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

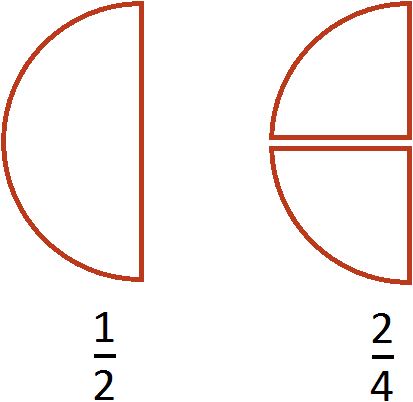
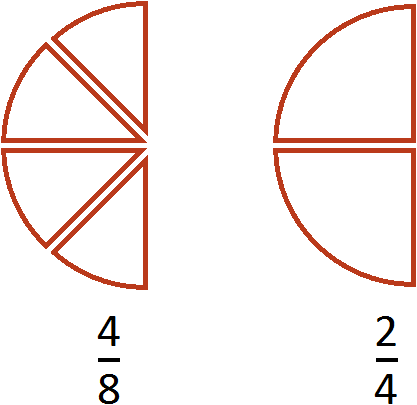
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник

Действия с дробями: правила, примеры, решения

Правила выполнения действий с числовыми дробями общего вида

Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:

Обоснование правил

Существуют следующие математические моменты, на которые следует опираться при вычислении:

С их помощью можно производить преобразования вида:

Примеры

В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.

Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.

Решение

Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:

Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что

Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.

Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.

Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.

Решение

2 3 5 + 1 + 1 2 = 2 · 2 2 · 3 5 + 1 + 1 · 3 5 + 1 2 · 3 5 + 1 = = 4 2 · 3 5 + 1 + 3 5 + 1 2 · 3 5 + 1 = 4 + 3 5 + 1 2 · 3 5 + 1 = 5 + 3 5 2 · 3 5 + 1

Ответ: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 · 3 5 + 1

Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.

Рассмотрим примеры умножений дробей общего вида.

Решение

Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:

5 · 3 3 2 + 1 : 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10

После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что

Выполнение действие с дробями, содержащими переменные

Примеры сложения и вычитания дробей с переменными

Решение

Рассмотрим двоякий способ решения.

Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида

В таком случае необходимо избавляться от иррациональности в знаменателе.

В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.

Решение

После чего получаем, что

Ответ:

Примеры умножения дробей с переменными

При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.

Решение

Необходимо выполнить умножение. Получаем, что

Деление

Возведение в степень

Порядок выполнения действий с дробями

Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.

Решение

1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x

Источник

Дроби и действия с дробями

Что такое дроби?

Вспоминаются примеры из начальной школы. Представьте себе пирог вкусный такой, и 4 голодных ребенка.

Как бы им так сделать, чтоб пирога досталось всем? Верно, надо его поделить, поделить один пирог на 4 человека:

На рисунке ты видишь пирог, разрезанный на 4 дольки. Так вот, как раз дробь – это и есть доля от целого.

Сегодня мы разберем подробно, что такое дроби. Как их правильно делить, умножать, вычитать, складывать, преобразовывать…

В общем, сегодня ты узнаешь о дробях ВСЕ, что нужно знать для успешной сдачи ОГЭ или ЕГЭ.

Дроби — коротко о главном

Определения:

Простая дробь (обыкновенная дробь) – запись рационального числа в виде отношения двух чисел \(\displaystyle\frac\).

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Правильная дробь – дробь, у которой числитель меньше знаменателя.

Например: \(\displaystyle\frac<2><5>\), \(\displaystyle\frac<1><7>\) и так далее.

Неправильная дробь –дробь, у которой числитель больше или равен знаменателю.

Например: \(\displaystyle\frac<9><5>\), \(\displaystyle\frac<13><2>\) и так далее.

Смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

Например: \(\displaystyle2\frac<2><5>\)\( \displaystyle \displaystyle=\frac<2\cdot 5><5>+\frac<2><5>=\frac<10><5>+\frac<2><5>=\frac<12><5>\).

Десятичная дробь – обыкновенная дробь со знаменателем \(\displaystyle10\), \(\displaystyle100\), \(\displaystyle1000\) и так далее, (т.е. \(\displaystyle<<10>^>\), где \(\displaystyle n\) — натуральное число).

Например: \(\displaystyle\frac<9><100>\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac<225><1000>\) записывается как \(\displaystyle0,225\).

Основное свойство дроби:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, дробь не изменится, несмотря на то, что выглядеть она будет по-другому.

Действия с дробями:

Сложение/вычитание дробей

Умножение дробей

Деление дробей

Сокращение дроби

Приведение дробей к наименьшему общему знаменателю

Например: \(\displaystyle\frac<1><3>\) и \(\displaystyle\frac<3><4>\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac<1\cdot 4><3\cdot 4>=\frac<4><12>\), для второй дроби: \(\displaystyle\frac<3\cdot 3><4\cdot 3>=\frac<9><12>\).

Преобразования неправильной дроби в смешанную дробь

Например: \(\displaystyle\frac<17><4>\) = \(\displaystyle4\frac<1><4>\).

Сравнение дробей:

Простые дроби

В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.

Это простая дробь.

Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac<1><4>\), \(\displaystyle <1>/<4>\;.\)

Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).

Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).

Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)

То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.

Можно запомнить так: Ч – чердак. Числитель сверху 🙂

Примеры простых дробей: \(\displaystyle 1/5,\text< >2/4,\text< >3/10,\text< >17/3.\)

Правильные и неправильные простые дроби

В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: \(\displaystyle 17/3\).

Если числитель больше знаменателя, то дробь называется неправильной.

Вне зависимости от того правильная дробь или неправильная, она будет простой.

Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?

Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?

Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.

А \(\displaystyle 17/3\)?

Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.

Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.

Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle 2\) куска.

А для целого пирога надо \( \displaystyle 3\) части. В итоге у нас \( \displaystyle 5\) целых и \( \displaystyle 2/3\) (две третьих) пирога.

Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle 5\frac<2><3>\) (пять целых и две третьих).

Смешанная дробь

То, что у нас получилось (\( \displaystyle 5\frac<2><3>\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

То, что между \( \displaystyle 5\) пирогами и \( \displaystyle 2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle 2x\).

Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle 5\frac<2><3>=5+\frac<2><3>\).

Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.

Ты же знаешь, как это сделать?

Преобразование из смешанной дроби в неправильную дробь.

В результате получим исходное \( \displaystyle 17/3\).

Источник

Дроби

Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.

Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.

Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.

А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.

Что такое дробь?

Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.

Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.

Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:

Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:

А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:

Такие записи называют дробями. Дробь состоит из числителя и знаменателя.

Число, которое записывается сверху, называется числителем дроби.

Число, которое записывается снизу, называется знаменателем дроби.

В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — в сё это синонимы.

Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?

Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):

Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?

Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:

Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:

Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам» :

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?

Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:

Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».

Дроби, которые мы сейчас рассмотрели, называют обыкновенными.

Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.

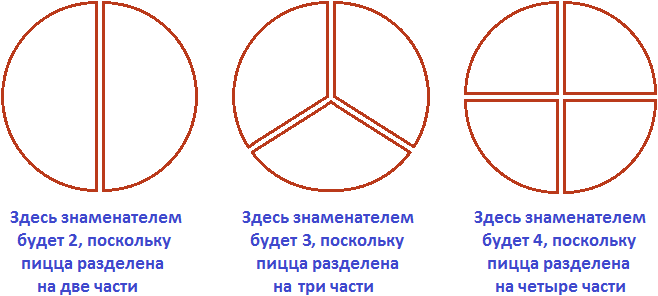
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.

На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.

Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли ( одну часть из двух ), или как говорят в народе «половину» пиццы.

С помощью переменных дробь можно записать так:

где a — это числитель, b — знаменатель.

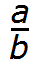
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:

Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём ( одну четвёртую ), то наш кусок будет меньше, чем все четыре куска вместе взятые ( чем одна целая пицца ). Поэтому такие дроби называют правильными.

С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:

Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.

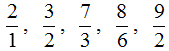
Теперь возьмём к примеру неправильную дробь 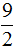и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.

Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:

Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь 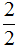. Применим её к нашей пицце.

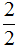
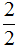
Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь 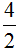. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

Выделение целой части дроби

Вычислим дробь 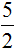. Пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Проверка: (2 × 2) + 1 = 4 + 1 = 5

Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.

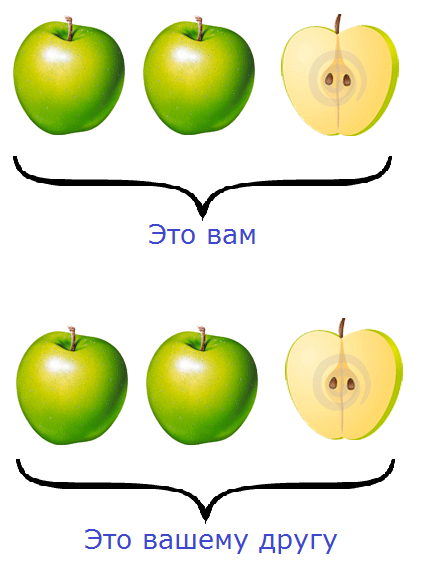
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?

Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:

Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.

Теперь возвращаемся к дроби 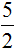и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:

Схематически это выглядит так:

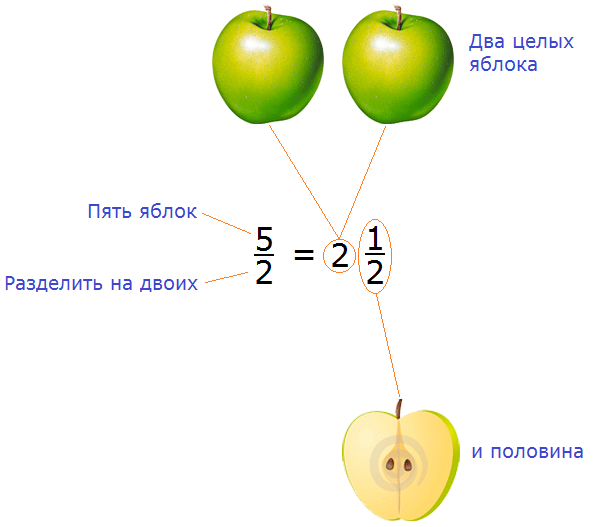
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.

В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.

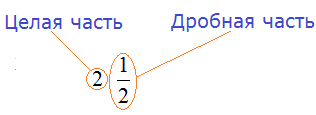
В нашем примере целая часть это 2, а дробная часть это

Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.

Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:

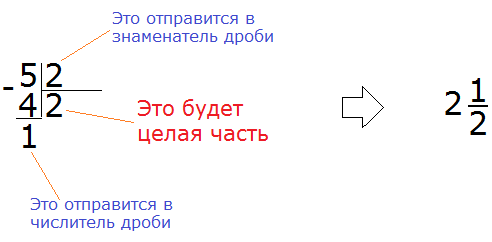
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби 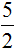. Записываем уголком данное выражение и решаем:

После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.

В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.

Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.

Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби

Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили:

Перевод смешанного числа в неправильную дробь

Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь 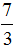. Если выделить в ней целую часть, то получается

Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.

Например, переведём смешанное число 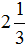в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:

Затем к 6 прибавляем числитель дробной части:

Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:

Подробное решение выглядит так:

А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:

Пример 2. Перевести смешанное число 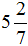в неправильную дробь.

Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.

Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

Сокращение дробей

Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .

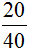
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.

Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.

Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.

Пример 1. Сократить дробь

Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.

В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2

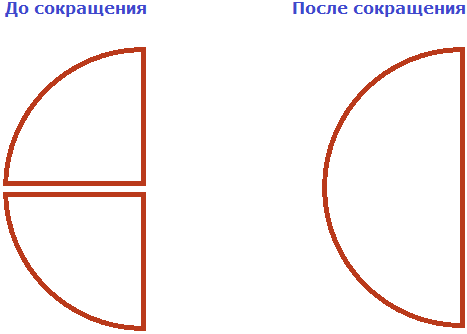
В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.

На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.

Пример 2. Сократим дробь

Чтобы сократить дробь 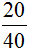, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.

НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби 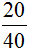на 20

Пример 3. Сократим дробь

Чтобы сократить дробь 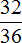, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.

НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби 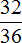на 4

Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:

Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.

Второй способ сокращения дроби

Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.

К примеру, вернёмся к дроби 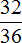. Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4

Теперь представьте, что в данном выражении отсутствует конструкция 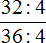, и сразу записан ответ . Получится следующее выражение:

Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.

Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:

Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:

Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36

Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.

Например, сократим дробь 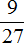, предварительно разложив на простые множители числитель и знаменатель:

Итак, мы разложили числитель и знаменатель дроби 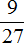на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.

Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:

Сократить можно ещё по тройке в числителе и в знаменателе:

Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.

Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.

Получили ответ . Значит, при сокращении дроби получается новая дробь .

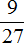
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.

Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:

Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:

Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?

Источник

Действия с дробями

Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.

Сложение дробей с одинаковыми знаменателями

Сложение дробей бывает двух видов:

Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.

Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:

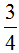
Пример 2. Сложить дроби и .

Опять же складываем числители, а знаменатель оставляем без изменения:

В ответе получилась неправильная дробь 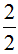. Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:

Пример 3. Сложить дроби и .

Опять же складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:

Пример 4. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:

Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.

Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:

Сложение дробей с разными знаменателями

Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.

Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.

А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.

Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.

Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.

Пример 1. Сложим дроби и

У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.

В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6

НОК (2 и 3) = 6

Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.

Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.

Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:

Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:

Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Таким образом, пример завершается. К прибавить получается .

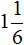
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:

Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).

Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).

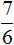
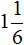
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:

Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.

Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.

Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:

Пример 2. Найти значение выражения .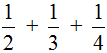

Воспользуемся инструкцией, которая приведена выше.

Шаг 1. Найти НОК знаменателей дробей

Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4

Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби

Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:

Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:

Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:

Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители

Умножаем числители и знаменатели на свои дополнительные множители:

Шаг 4. Сложить дроби у которых одинаковые знаменатели

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:

Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.

Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть

У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:

Получили ответ

Вычитание дробей с одинаковыми знаменателями

Вычитание дробей бывает двух видов:

Сначала изучим вычитание дробей с одинаковыми знаменателями.

Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.

Например, найдём значение выражения 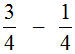. Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от 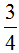пиццы отрезать пиццы, то получится пиццы:

Пример 2. Найти значение выражения .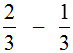

Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:

Пример 3. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:

Вычитание дробей с разными знаменателями

Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.

Например, от дроби 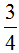можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.

Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.

Пример 1. Найти значение выражения:

У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.

Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12

НОК (3 и 4) = 12

Теперь возвращаемся к дробям и

Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:

Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Получили ответ

Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы

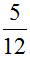
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:

Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):

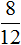
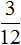
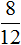
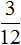
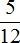
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.

Пример 2. Найти значение выражения

У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.

Найдём НОК знаменателей этих дробей.

Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30

НОК (10, 3, 5) = 30

Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.

Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:

Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:

Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:

Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.

Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:

В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.

Чтобы сократить дробь 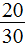, нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.

Итак, находим НОД чисел 20 и 30:

Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби 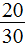на найденный НОД, то есть на 10

Получили ответ

Умножение дроби на число

Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.

Умножим числитель дроби на число 1

Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы

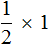
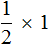
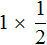
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:

Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:

Пример 2. Найти значение выражения

Умножим числитель дроби на 4

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Выражение 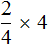можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы

А если поменять множимое и множитель местами, то получим выражение 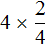. Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:

Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.

Например, выражение 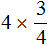можно вычислить двумя способами.

Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:

Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:

Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:

А вот к примеру выражение 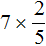можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:

Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.

Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:

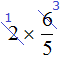
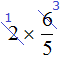
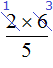
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.

Умножение дробей

Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.

Пример 1. Найти значение выражения .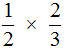

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

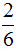
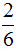
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:

Выражение 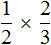можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:

У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:

Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения 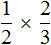равно

Пример 2. Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Пример 3. Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.

Итак, найдём НОД чисел 105 и 450:

Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15

Представление целого числа в виде дроби

Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:

Обратные числа

Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».

Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.

Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:

Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.

Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:

Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:

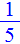
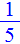
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.

Обратное число можно найти также для любого другого целого числа.

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.

Деление дроби на число

Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на

Получили ответ . Значит при делении половины на две части получается четверть.

Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:

Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:

Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:

Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь

В обоих случаях получился один и тот же результат.

Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь

Пример 2. Найти значение выражения

Умножим первую дробь на число, обратное делителю:

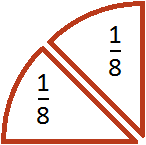
Допустим, имеется четверть пиццы и нужно разделить её на двоих:

Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:

Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5

Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь

Как видно результат не изменился. Мы снова получили ответ 5.

Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.

Пример 3. Найти значение выражения

Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь

Допустим, имелось пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков

Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается

Деление числа на дробь

Правило деления числа на дробь такое же, как и правило деления дроби на число.

Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.

Например, разделим число 1 на .

Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь

Выражение 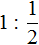можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:

Пример 2. Найти значение выражения

Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь

Допустим, у нас имеются две целые пиццы:

Деление дробей

Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.

Например, разделим на

Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь

Допустим, имеется половина пиццы:

Пример 1. Найти значение выражения

Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:

Пример 2. Найти значение выражения

Умножаем первую дробь на дробь обратную второй:

Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.

Каждая следующая тема будет более сложной, поэтому нужно тренироваться.

Источник