если график распределения переменной имеет симметричную форму то
Виды распределений
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход и т.п., а потом построить график любой из этих величин, то получится функция распределения данной величины. В зависимости от исследуемого признака получаемые графики могут быть различны.
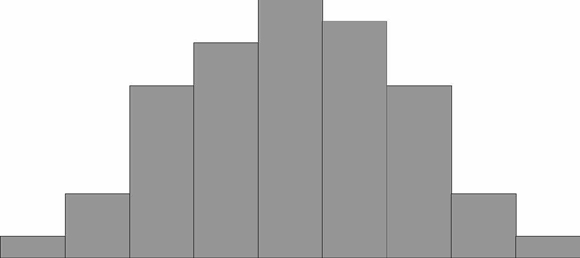
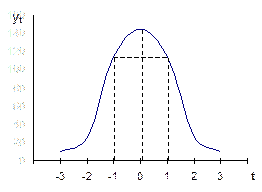
Посмотрим, как можно построить такой график на примере данных роста. Сначала, просто запишем результаты исследования. Потом, отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно». После этого необходимо посчитать количество людей в каждой подгруппе (диапазоне) – это будет частота попадания роста жителей города в данный диапазон. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить гистограмму – упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а высота будет равна той частоте, которая соответствует каждому диапазону роста. Если зарегистрированных данных было достаточно много, то полученный график будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения:
Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие.
Выделяют большое количество видов распределения признака в статистической совокупности. Остановимся на их краткой характеристике:
1) нормальное распределение
2) асимметричное распределение
3) альтернативное распределение
Нормальное (Гауссово, симметричное, колоколообразное) распределение– одно из самых важных распределений в статистике. Оно характеризуется тем, что наибольшее число наблюдений имеет значение, близкое к среднему, и чем больше значения отличаются от среднего, тем меньше таких наблюдений. Примерами характеристик, подчиняющихся нормальному распределению, являются показатели роста, веса, какие-либо биохимические показатели крови.
Гауссово распределение характеризует распределение непрерывных случайных величин и встречается в природе наиболее часто, за что и получило название «нормального».
Кривая нормального распределения имеет следующие свойства:
· симметрична относительно среднего;
· сдвигается вправо, если среднее увеличивается, и влево, если среднее уменьшается (при постоянной дисперсии).
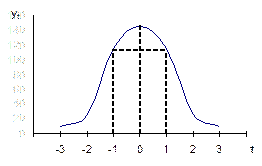
Среднее арифметическое, мода и медиана при нормальном распределении равны и соответствуют вершине распределения:
Нормальное распределение описывает явления, которые носят вероятностный, слу 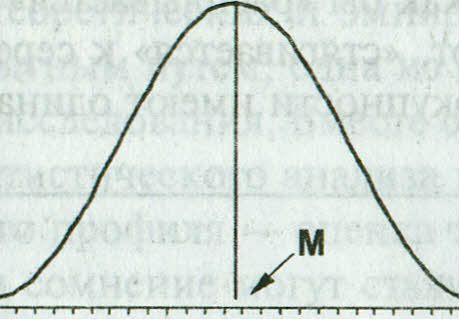
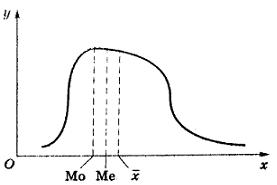
При асимметричном распределении данных наиболее полезной мерой центральной тенденции становится медиана. Это связано с тем, что на простую среднюю арифметическую сильно влияют экстремальные (очень высокие или очень низкие) значения, из-за чего она может стать причиной неверной интерпретации результатов. Медиана же менее подвержена влиянию экстремальных величин.
Если график распределения имеет правостороннюю асимметрию («хвост» вправо, в вариационном ряду преобладают варианты меньших значений), то в этом случае мода размещена левее, а среднее арифметическое (на рисунке обозначено как 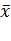
Обратное расположение имеет место при левосторонней асимметрии графика. При этом, чем больше асимметричен график, тем больше расстояние между его средними точками.
Проиллюстрируем важность выбора медианы, а не среднего арифметического значения на следующем примере. График заработной платы для жителей России имеет правостороннее асимметричное распределение (большинство людей имеет небольшую заработную плату). В силу того, что разброс минимальной и максимальной величин заработной платы очень велик, экстремальные значения сильно сказываются на значении среднего арифметического М (на рисунке обозначено как 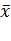
Бимодальное (двугорбое) распределениенаблюдается тогда, когда исследуемый признак анализируется вне однородной совокупности и, следовательно, необходимо учитывать два средних значения признака для достоверного анализа. Пример: при оценке физического развития детей подростков распределение роста будет иметь две моды (соответствующие девочкам и мальчикам).
Альтернативное распределениенаблюдается в том случае, когда значения исследуемого признака распределяются по принципу: «да/нет», т.е. взаимоисключают друг друга. Подобное распределение характерно для описания качественных признаков (пример: мужской, женский пол).
Использование средних величин в медицине и здравоохранении:
а) для оценки состояния здоровья — например, параметров физического развития (средний рост, средний вес, средний объем жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средний пульс, средняя СОЭ и др.);
б) для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений за 1 ч. приема в поликлинике и др.);
в) для оценки состояния окружающей среды.
В медицинских исследованиях из средних величин наиболее часто используется среднее арифметическое. В то же время, у больных людей значения многих физиологических параметров имеют асимметричное распределение, ввиду того, что изменяются в сторону увеличения или уменьшения под влиянием заболевания. Поэтому для характеристики центральной тенденции их распределения, во многих случаях, более обоснованным является как раз использование медианы, а не средней арифметической.
1. Вопросы по теме занятия:
1. Понятия генеральной и выборочной совокупностей.
2. Репрезентативность выборочной совокупности, качественная и количественная репрезентативность.
3. Одномерные, двумерные и многомерные наборы данных, понятия и примеры.
4. Виды признаков: качественные, порядковые, количественные. Их характеристика, примеры.
5. Факторные и результативные признаки.
6. Понятие временного ряда, медико-биологические примеры.
7. Шкалы измерения признаков.
8. Понятие вариационного ряда, его характеристики.
9. Виды вариационных рядов.
10. Понятия среднего арифметического, моды и медианы для вариационного ряда. Расчет этих характеристик.
11. Примеры использования среднего арифметического, моды и медианы в медицинских исследованиях.
12. Виды распределения случайной величины.
13. Мода, медиана и среднее арифметическое для нормального и ассиметричного распределений.
2. Тестовые задания по теме с эталонами ответов:
1. СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ – ЭТО
1) группа определенных признаков
2) группа объектов, обладающих признаками сходства и различия
3) группа относительно однородных элементов (единиц наблюдения), взятых в единых границах времени и пространства
4) группа явлений, объединенных в соответствии с целью исследования
2. ПЕРВИЧНЫМ ЭЛЕМЕНТОМ СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ ЯВЛЯЕТСЯ
1) объект наблюдения
3) единица наблюдения
4) группа признаков
3. ЕДИНИЦА НАБЛЮДЕНИЯ В СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ – ЭТО
2) первичный элемент совокупности, обладающий учитываемыми признаками
3) группа признаков
4. ЕДИНИЦА СОВОКУПНОСТИ – ЭТО
1) описка по рассеянности или невнимательности
2) первичный элемент объекта статистического наблюдения, являющийся носителем признаков, подлежащих регистрации
3) разметка бланков по условным знакам
4) первичный элемент, из которых состоит вся наблюдаемая статистическая совокупность
1) объект статистического исследования
2) первичный элемент статистической совокупности
3) свойство, проявлением которого один предмет отличается от другого
4) характеристика статистической совокупности
6. К КАЧЕСТВЕННЫМ ПРИЗНАКАМ ОТНОСЯТСЯ
4) жизненная емкость легких
7. К КОЛИЧЕСТВЕННЫМ ПРИЗНАКАМ ОТНОСЯТСЯ
3) исход заболевания
8. ВЫБОРОЧНАЯ СОВОКУПНОСТЬ ЭТО
1) группа, состоящая из относительно однородных элементов, взятых в единых границах времени и пространства
2) совокупность, состоящая из всех единиц наблюдения, которые могут быть к ней отнесены в соответствии с целью исследования
3) часть генеральной совокупности, отобранная специальными методами и предназначенная для ее характерис-тики
4) совокупность всех единиц наблюдения, которые могут быть отнесены к ней в соответствии с целью исследования
9. РЕПРЕЗЕНТАТИВНОСТЬ – ЭТО
1) достаточный объем генеральной совокупности
2) достаточный объем выборочной совокупности
3) непохожесть выборочной совокупности на генеральную
4) способность выборочной совокупности наиболее полно представлять генеральную
10. РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНОЙ СОВОКУПНОСТИ ПО ОТНОШЕНИЮ К ГЕНЕРАЛЬНОЙ ОБЕСПЕЧИВАЕТ
1) обязательное соблюдение временных границ
2) достаточный объем наблюдений
3) оценка показателей в динамике
4) обязательное соблюдение пространственных границ
11. ДОСТОИНСТВА СРЕДНЕЙ ВЕЛИЧИНЫ СОСТОЯТ В ТОМ, ЧТО ОНА
1) позволяет анализировать большое число наблюдений
2) позволяет выявить закономерности при малом числе наблюдений и большом разбросе показателей
3) позволяет с помощью одного числа получить представления о совокупности массовых явлений
4) позволяет с помощью одного числа получить представления о распространенности массовых явлений
12. ЕДИНИЦА НАБЛЮДЕНИЯ ОПРЕДЕЛЯЕТСЯ В ЗАВИСИМОСТИ ОТ
1) программы исследования
2) плана исследования
3) цели и задач исследования
4) количества наблюдений
13. ВАРИАЦИОННЫЙ РЯД – ЭТО
1) ряд числовых измерений признака, расположенных в ранговом порядке и характеризующихся определенной частотой
2) ряд цифровых значений различных признаков
3) генеральная совокупность
4) ряд чисел, отражающих частоту (повторяемость) цифровых значений изучаемого признака
14. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ – ЭТО
1) варианта с наибольшей частотой
2) разность между наибольшей и наименьшей величиной
3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности
4) варианта, находящаяся в середине ряда
1) варианта с наибольшей частотой
2) разность между наибольшей и наименьшей величиной
3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности
4) варианта, находящаяся в середине ряда
1) варианта с наибольшей частотой
2) разность между наибольшей и наименьшей величиной
3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности
4) варианта, находящаяся в середине ряда
17. ПРОЦЕСС СЛУЧАЙНОГО ОТБОРА ДАННЫХ НАЗЫВАЕТСЯ
18. ПРИЗНАК: «НАЛИЧИЕ ИЛИ ОТСУТСТВИЕ БОЛЕЗНИ» ЯВЛЯЕТСЯ
19. ЗАВИСИМЫЙ ПРИЗНАК, ИЗМЕНЯЮЩИЙ СВОЕ ЗНАЧЕНИЕ ПОД ВЛИЯНИЕМ ДРУГОГО, НАЗЫВАЕТСЯ
20. ШКАЛА, УКАЗЫВАЮЩАЯ СТЕПЕНЬ ВЫРАЖЕННОСТИ ПРИЗНАКА
21. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ СОСТОИТ ИЗ
1) отдельных единиц наблюдения, взятых в известных границах времени и пространства
2) всех единиц наблюдения, которые могут быть отнесены к ней в соответствии с целью исследования
3) всех единиц наблюдения, которые могут быть отнесены к ней независимо от цели исследования
4) всех единиц наблюдения, обладающих определенным признаком
22. ОДНОЙ ИЗ СРЕДНИХ ВЕЛИЧИН ЯВЛЯЕТСЯ
1) показатель соотношения
3) среднее квадратическое отклонение
4) интенсивный показатель
23. ОТНОШЕНИЕ СУММЫ ЗНАЧЕНИЙ ВСЕХ ВАРИАНТ К ОБЩЕМУ ИХ КОЛИЧЕСТВУ – ЭТО
2) средняя арифметическая
4) среднее квадратическое отклонение
24. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА ПРИМЕНЯЕТСЯ В ЦЕЛЯХ
1) обобщения числовых характеристик варьирующего явления при разработке или сводке материала
2) обобщения качественных характеристик
3) сравнения и сопоставления явлений
4) разработки нормативов
25. ИЗ ПРИВЕДЕННЫХ СРЕДНИХ НАИБОЛЕЕ ЧАСТО В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ ИСПОЛЬЗУЮТСЯ
1) средняя геометрическая
2) средняя арифметическая
3) средняя гармоническая
4) средняя алгебраическая
26. ВЕЛИЧИНЫ, РАЗБИВАЮЩИЕ ВАРИАЦИОННЫЙ РЯД НА ОТДЕЛЬНЫЕ (ПО ВОЗМОЖНОСТИ РАВНЫЕ) ЧАСТИ, ЭТО
3) ошибки средних величин
27. НА ЧЕТЫРЕ РАВНЫЕ ЧАСТИ ВАРИАЦИОННЫЙ РЯД РАЗДЕЛЯЮТ
28. ЕСЛИ ДВА СОСЕДНИХ ЗНАЧЕНИЯ ВАРИАЦИОННОГО РЯДА ИМЕЮТ ОДИНАКОВУЮ ЧАСТОТУ, ТО
1) ряд не имеет моды
2) мода равняется среднему арифметическому этих значений
3) вариационный ряд имеет две моды
4) модой является число, стоящее ближе к середине ряда
29. ЕСЛИ ДВА ЗНАЧЕНИЯ ВАРИАЦИОННОГО РЯДА, НЕ ЯВЛЯЮЩИЕСЯ СОСЕДНИМИ, ИМЕЮТ ОДИНАКОВУЮ ЧАСТОТУ, ТО
1) ряд не имеет моды
2) мода равняется среднему арифметическому этих значений
3) вариационный ряд имеет две моды
4) модой является число, стоящее ближе к середине ряда
30. В ЗАВИСИМОСТИ ОТ ВИДА СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАЗЛИЧАЮТ СЛЕДУЮЩИЕ ВИДЫ ВАРИАЦИОННЫХ РЯДОВ
1) несгруппированный и сгруппированный
2) моментный и интервальный
3) дискретный и непрерывный
4) простой и сложный
31. КАЧЕСТВЕННЫЕ ДАННЫЕ, КОТОРЫЕ МОГУТ БЫТЬ ОТНЕСЕНЫ ТОЛЬКО К ДВУМ ПРОТИВОПОЛОЖНЫМ КАТЕГОРИЯМ, ПРИНИМАЮЩИЕ ОДНО ИЗ ДВУХ ЗНАЧЕНИЙ, НАЗЫВАЮТСЯ
32. КОЛИЧЕСТВЕННЫЕ ПРИЗНАКИ, ПРИНИМАЮЩИЕ ЗНАЧЕНИЯ ЛИШЬ ИЗ НЕКОТОРОГО СПИСКА ОПРЕДЕЛЕННЫХ ЧИСЕЛ, ОБЫЧНО ЦЕЛЫХ, НАЗЫВАЮТСЯ
33. РЯД ПОСЛЕДОВАТЕЛЬНЫХ ЗНАЧЕНИЙ, ХАРАКТЕРИЗУЮЩИХ ИЗМЕНЕНИЕ ПОКАЗАТЕЛЯ ВО ВРЕМЕНИ, И ИМЕЮЩИЙ СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ, ЭТО
3) произвольный ряд
4) вариационный ряд
34. ДАННЫЕ, СОДЕРЖАЩИЕ ИНФОРМАЦИЮ О ТРЕХ ИЛИ БОЛЕЕ ПРИЗНАКАХ ДЛЯ КАЖДОГО ОБЪЕКТА, НАЗЫВАЮТСЯ
35. КАЖДОЕ ЧИСЛОВОЕ ЗНАЧЕНИЕ В ВАРИАЦИОННОМ РЯДУ НАЗЫВАЮТ
36. ПРИ ПРАВОСТОРОННЕЙ АСИММЕТРИИ СЛЕВА НАПРАВО РАСПОЛОЖЕНЫ
1) мода, медиана и среднее арифметическое совпадают
2) мода, далее медиана, затем среднее арифметическое
3) среднее арифметическое, далее медиана, потом мода
4) среднее арифметическое, мода, медиана
37. ЕСЛИ ГРАФИК РАСПРЕДЕЛЕНИЯ ИМЕЕТ СИММЕТРИЧНУЮ ФОРМУ, ТО
1) левее расположена мода, затем медиана и среднее арифметическое
2) левее расположена среднее арифметическое, затем медиана и мода
3) левее расположено среднее арифметическое, затем мода и медиана
4) мода, медиана и среднее арифметическое совпадают
38. ЕСЛИ ВСЕ ЗНАЧЕНИЯ В ВАРИАЦИОННОМ РЯДУ ВСТРЕЧАЮТСЯ ОДИНАКОВО ЧАСТО, СЧИТАЕТСЯ, ЧТО ЭТОТ РЯД
39. КОЛИЧЕСТВЕННЫЕ ПРИЗНАКИ, ПРИНИМАЮЩИЕ ЛЮБОЕ ЗНАЧЕНИЕ НА НЕПРЕРЫВНОЙ ШКАЛЕ, НАЗЫВАЮТСЯ
40. РЕПРЕЗЕНТАТИВНОСТЬ, ОБОЗНАЧАЮЩАЯ СТРУКТУРНОЕ СООТВЕТСТВИЕ ВЫБОРОЧНОЙ И ГЕНЕРАЛЬНОЙ СОВОКУПНОСТЕЙ, НАЗЫВАЕТСЯ
Эталоны ответов к тестовым заданиям:
Определение симметричного распределения
Опубликовано 30.05.2021 · Обновлено 30.05.2021
Что такое симметричное распределение?
Симметричное распределение возникает, когда значения переменных встречаются с регулярными частотами, а среднее значение, медиана и мода – в одной и той же точке. В форме графика симметричное распределение часто выглядит как колоколообразная кривая. Если провести линию, рассекающую середину графика, то будут показаны две стороны, отражающие друг друга. Симметричное распределение – это основная концепция технической торговли, поскольку предполагается, что динамика цены актива соответствует симметричной кривой распределения во времени.
Ключевые выводы
Что вам говорит симметричное распределение?
Симметричное распределение используется трейдерами для определения области стоимости акции, валюты или товара на заданном временном интервале. Эти временные рамки могут быть внутридневными, например 30-минутными интервалами, или более долгосрочными с использованием сессий или даже недель и месяцев. Кривая колокола может быть проведена вокруг ценовых точек, достигнутых в течение этого периода времени, и ожидается, что большая часть ценового действия – примерно 68% ценовых точек – будет находиться в пределах одного стандартного отклонения от центра кривой. Кривая применяется к оси Y (цена), поскольку это переменная, тогда как время на протяжении всего периода просто линейно. Таким образом, область в пределах одного стандартного отклонения от среднего – это область значений, в которой цена и фактическая стоимость актива наиболее точно соответствуют друг другу.
Если ценовое действие выводит цену актива за пределы области значений, это говорит о том, что цена и стоимость не совпадают. Если прорыв находится в нижней части кривой, актив считается недооцененным. Если он находится на вершине кривой, актив следует переоценить. Предполагается, что актив со временем вернется к среднему значению.
Пример использования симметричного распределения
Симметричное распределение чаще всего используется для того, чтобы поместить ценовое действие в контекст. Чем дальше движение цены отклоняется от области значений на одно стандартное отклонение с каждой стороны от среднего, тем больше вероятность того, что базовый актив недооценен или переоценен рынком. Это наблюдение предложит потенциальные сделки для размещения в зависимости от того, насколько далеко отклонилось ценовое действие от среднего значения за используемый период времени. Однако в более крупных временных масштабах риск упустить фактические точки входа и выхода гораздо выше.
Симметричное распределение против асимметричного распределения
Противоположное симметричное распределение – это асимметричное распределение. Распределение считается асимметричным, если оно не симметрично с нулевой асимметрией; другими словами, это не перекос. Асимметричное распределение либо скошено влево, либо вправо. Распределение с перекосом влево, так называемое отрицательное распределение, имеет более длинный левый хвост. Распределение с уклоном вправо или с положительным уклоном имеет более длинный правый хвост. Определение того, является ли среднее значение положительным или отрицательным, важно при анализе перекоса набора данных, поскольку это влияет на анализ распределения данных.
Асимметрия часто является важным компонентом анализа трейдером потенциальной доходности инвестиций. Симметричное распределение доходов равномерно распределяется вокруг среднего значения. Асимметричное распределение с положительным перекосом вправо указывает на то, что историческая доходность, отклоняющаяся от среднего, была в основном сосредоточена на левой стороне кривой колокола. И наоборот, отрицательный сдвиг влево показывает отклонение исторической доходности от среднего, сконцентрированного на правой стороне кривой.
Ограничения симметричного распределения
Распространенный отказ от инвестиций заключается в том, что прошлые результаты не гарантируют будущих результатов; однако прошлые результаты могут проиллюстрировать закономерности и дать понимание трейдерам, желающим принять решение по позиции. Симметричное распределение – это общее практическое правило, но независимо от используемого периода времени часто будут периоды асимметричного распределения на этой временной шкале. Это означает, что, хотя колоколообразная кривая обычно возвращается к симметрии, могут быть периоды асимметрии, которые устанавливают новое среднее значение для центра кривой. Это означает, что торговля, основанная исключительно на области значений симметричного распределения, может быть рискованной, если сделки не подтверждаются другими техническими индикаторами.
Симметричные и асимметричные распределения. Показатели асимметрии и эксцесса для характеристики асимметричных рядов распределения



При анализе вариационных рядов смещение от центра и крутизну распределения характеризуют специальные показатели. Эмпирические распределения, как правило, смещены от центра распределения вправо или влево, асимметричны. Нормальное распределение строго симметрично относительно средней арифметической, что обусловлено четностью функции.
Асимметрия распределения возникает вследствие того, что какие-либо факторы действуют в одном направлении сильнее, чем в другом, или процесс развития явления таков, что доминирует какая-то причина. Кроме того, природа некоторых явлений такова, что имеет место асимметричное распределение.
Наиболее простой мерой асимметрии является разность между средней арифметической, модой и медианой:
— в симметричном ряду: 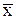
— при правосторонней асимметрии: Мо Ме > 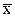
Для определения направления и величины смещения (асимметрии) распределения рассчитывается коэффициент асимметрии, представляющий собой нормированный момент третьего порядка:
| Рис. Асимметрия распределения: а – правосторонняя; б – левосторонняя | Рис. Характеристика распределений в соответствии с эксцессом: 1 – высоковершинное; 2 – нормальное; 3 – низковершинное |
Соотношение между модой, медианой и средней арифметической в симметричном и асимметричном рядах позволяет в качестве меры асимметрии использовать более простой показатель коэффициента асимметрии Пирсона:
Ex = (m4/s 4 ) – 3, где: m 4 – центральный момент четвертого порядка.
У высоковершинных кривых эксцесс положительный, у низковершинных отрицательный (рис. Г.2).
Показатели эксцесса и асимметрии необходимы в статистическом анализе для определения неоднородности совокупности, асимметричности распределения и близости эмпирического распределения к нормальному закону. При значительных отклонениях показателей асимметрии и эксцесса от нуля нельзя признать совокупность однородной, а распределение близким к нормальному. Сопоставление фактических кривых с теоретическими позволяет математически обосновать полученные статистические результаты, установить тип и характер распределения социально-экономических явлений, прогнозировать вероятность появления изучаемых событий.
Обоснование близости эмпирического (фактического) распределения к теоретическому нормальному распределению. Нормальное распределение (закон Гаусса-Лапласа) и его характеристики. «Правило трех сигм». Критерии согласия (на примере критерия Пирсона или Колгомогорова).
Можно заметить определенную связь в изменении частот и значений варьирующего признака. Частоты с ростом значения признака сначала увеличиваются, а затем после достижения какой-то максимальной величины уменьшаются. Такие закономерные изменения частот в вариационных рядах называются закономерностями распределения.
Для выявления закономерности распределения необходимо, чтобы вариационный ряд содержал достаточно большое количество единиц, а сами ряды представляли собой качественно однородные совокупности.
В практической работе закон распределения находят путем сравнения эмпирического распределения с одним из теоретических и оценки степени различия или соответствия между ними. Теоретическая кривая распределения отражает в чистом виде, без учета влияния случайных факторов, общую закономерность распределения частот (плотности распределения) в зависимости от значений варьирующих признаков.
В статистике распространены различные виды теоретических распределений: нормальное, биномиальное, Пуассона и др. Каждое из теоретических распределений имеет свою специфику и область применения.
Закон нормального распределения характерен для распределения равновероятных событий, происходящих при взаимодействии множества случайных факторов. Закон нормального распределения лежит в основе статистических методов оценки параметров распределения, репрезентативности выборочных наблюдений, измерения взаимосвязи массовых явлений.
Для проверки, насколько фактическое распределение соответствует нормальному, необходимо сравнить частоты фактического распределения с теоретическими частотами, характерными для нормального закона распределения. Эти частоты являются функцией нормированных отклонений. Поэтому по данным эмпирического ряда распределения вычисляют нормированные отклонения t. Затем определяют соответствующие им теоретические частоты. Таким образом, выравнивается эмпирическое распределение.
Нормальное распределение или закон Гаусса-Лапласа описывается уравнением 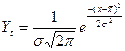
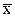
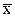
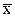
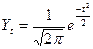
Нормальное распределение характеризуется двумя существенными параметрами, определяющими центр группирования индивидуальных значений и форму кривой: средней арифметической 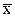
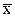
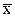
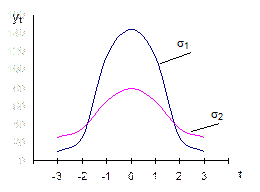
| Рис. Г.3. Нормальное распределение | Рис. Г.4. Нормальное распределение с различными дисперсиями (s1 2 2 ) |
Кривая нормального распределения имеет две точки перегиба (переход от выпуклости к вогнутости) при t = ±1, т.е. при отклонении вариантов от средней (х – 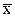
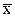
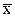
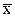
Для расчета теоретических частот применяется формула:
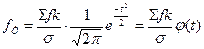
Величина 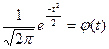
Таблица 9.1. Значения плотности нормального распределения
| t | j(t) | t | j(t) | t | j(t) | t | j(t) |
| 0,0 0,2 0,4 0,6 0,8 | 0,3989 0,3910 0,3683 0,3332 0,2897 | 1,0 1,2 1,4 1,6 1,8 | 0,2420 0,1942 0,1497 0,1109 0,0790 | 2,0 2,2 2,4 2,6 2,8 | 0,0540 0,0355 0,0224 0,0136 0,0079 | 3,0 3,2 3,4 3,6 3,8 | 0,0044 0,0024 0,0012 0,0006 0,0003 |
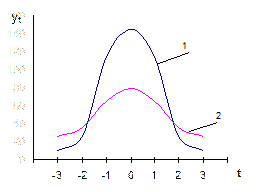
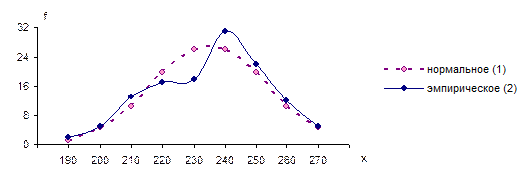
График на рис. 9.1 наглядно демонстрирует близость эмпирического (2) и нормального (1) распределений.
Рис. 9.1. Распределения филиалов почтовой связи по численности работников: 1 – нормальное; 2 – эмпирическое.
На основании значения Р(l) делают определенные выводы: если вероятность Р(l) достаточно велика, то гипотезу о соответствии фактического распределения нормальному закону можно считать подтвержденной; если вероятность Р(l) мала, то нулевая гипотеза отвергается, расхождения между фактическим и теоретическим распределениями признаются существенными.
Значения вероятностей для критерия согласия l:
| l | Р(l) | l | Р(l) | l | Р(l) |
| 0,3 | 1,000 | 0,8 | 0,544 | 1,5 | 0,022 |
| 0,4 | 0,997 | 0,9 | 0,399 | 1,8 | 0,013 |
| 0,5 | 0,964 | 1,0 | 0,27 | 2,0 | 0,006 |
| 0,6 | 0,864 | 1,1 | 0,18 | 2,1 | 0,003 |
| 0,7 | 0,711 | 1,2 | 0,11 | 2,3 | 0,000 |
Уровень значимости выбирается так, что Р(c 2 расч>c 2 табл) = a. Число степеней свободы равно h–l, где h – число групп; l – число условий, которые должны выполняться при вычислении теоретических частот. Для расчета теоретических частот кривой нормального распределения по формуле 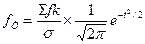
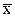
В этом случае нулевая гипотеза отвергается. Если c 2 расч£ c 2 табл, т.е. рассчитанный критерий не превышает максимально возможное расхождение частот, которое может возникнуть в силу случайности, то в данном случае гипотеза о соответствии распределений принимается. Критерий Пирсона эффективен при значительном числе наблюдений (n³50), причем частоты всех интервалов должны насчитывать не менее пяти единиц (при меньшем количестве интервалы объединяют), а число интервалов (групп) должно быть большим (h>5), поскольку оценка c 2 зависит от числа степеней свободы.
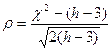
Если отношение больше 3, то расхождение частот эмпирического и нормального распределений нельзя признать случайным и гипотезу о нормальном законе распределения следует отвергнуть. Если отношение меньше или равно 3, то можно принять гипотезу о нормальном характере распределения данных.