если операцию над отношением называют фильтрацией то саму логическую функцию называют
Если операцию над отношением называют фильтрацией то саму логическую функцию называют

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Информатика. 10 класс
Тезаурус
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.
Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным.
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
Инверсия — логическая операция, при которой высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.
Конъюнкция — логическая операция, ставящая в соответствие двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба высказывания истинны.
Дизъюнкция — логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба высказывания ложны.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений входящих в него переменных, называют таблицей истинности логического выражения.
Истинность логического выражения можно доказать путем построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
Список литературы
Основная литература по теме урока:
— Л. Л.Босова, А. Ю.Босова. Информатика. Базовый уровень: учебник для 10 класса. — М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197)
Дополнительная литература по теме урока:
— К. Ю.Поляков, Е. А.Еремин. Информатика углубленный уровень: учебник для 10 класса: часть 1. — М.: БИНОМ. Лаборатория знаний, 2013 (с.159—196)
Открытые электронные ресурсы по теме:
Если операцию над отношением называют фильтрацией то саму логическую функцию называют
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности
Представление логической функции в виде таблицы истинности
Прежде всего, определимся с понятием «элементарная логическая функция». Чаще всего,это понятие в литературе никак не расшифровывается. В дальнейшем мы будем понимать под «элементарной логической функцией» ФАЛ от аргументов, каждый из которых, в свою очередь, не является логической функцией и которые имеют своё собственное обозначение.
Таблица истинности указывает значение логической функции при всех значениях наборов аргументов. Ниже мы рассмотрим элементарные логические функции от одной и двух переменных.
Все возможные элементарные логические функции от одной переменной представлены в Табл. 1.1:
| Функция | x | Наименование функции | Обозначение функции | |
|---|---|---|---|---|
| x=0 | x=1 | |||
| ƒ0 | 0 | 0 | Константа «ноль» | ƒ(x)=0 |
| ƒ1 | 0 | 1 | Тождественная функция | ƒ(x)=x |
| ƒ2 | 1 | 0 | Отрицание | 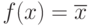 |
| ƒ3 | 1 | 1 | Константа «единица» | ƒ(x)=1 |
Здесь интерес представляет лишь одна функция – отрицание. Опишем ее основные свойства:
Последнее свойств можно описать как «отрицание отрицания есть утверждение».
Все возможные логические функции от двух переменных представлены в Табл. 1.2:
Тест на тему: «Математическая логика и теория алгоритмов».
Тест содержит 20 заданий, на которые отводится 60 минут. Рекомендуется выполнять задания по порядку, не пропуская ни одного.
Просмотр содержимого документа
«Тест на тему: «Математическая логика и теория алгоритмов».»
Тест содержит 20 заданий, на которые отводится 60 минут. Рекомендуется выполнять задания по порядку, не пропуская ни одного.
Прочитайте тест внимательно. Правильные задания обведите кружком или поставьте крестик.
Если не удается выполнить задание сразу, то перейдите к следующему. Если останется время, вернитесь к пропущенным заданиям.
Если ошиблись и обвели не тот вариант ответа, зачеркните, и отметьте верный (кружок или крестик).
Ответ на задание состоит из одного слова, числа или целого выражения.
Тест.
Тема: «Математическая логика и теория алгоритмов».
2. Чему равен натуральный показатель n в бинарной операции?
3. Укажите верную формулу закона упрощения:
4. …- это композиция функций (сложная функция).
5. Что называют конечным полным множеством?
6. Вставьте пропущенное слово в следующее высказывание: «Если F — полное множество булевых функций, каждая из которых представима формулой над множеством G, то и G — … множество».
7. Родина Джорджа Буля
8. Величайший древнегреческий философ, которым были заложены основы логики, науки о законах и формах человеческого мышления.
9. Укажите ученого из перечисленных ниже, который рассмотрел в 1666 году вопрос о создании символической логики, как универсального научного языка в работе «Искусство комбинаторики».
10. Выполняемые высказывания – это высказывания…
а) имеющие значение 1 хотя бы для одного набора значений пропозициональных переменных;
б) ложные при любой истинности переменных;
в) имеющие значение 0 хотя бы для одного набора значений пропозициональных переменных;
г) истинные при любой истинности переменных.
11. Установите соответствие между названием тезиса и его описанием.
Ответ занесите в таблицу.
а) Согласно этому тезису, всякая вычислимая в интуитивном
смысле функция вычислима с помощью некоторой машины названной в честь автора данного тезиса.
б) Этот тезис является гипотезой. Его невозможно строго доказать (так же, как и тезис Тьюринга).
Для того чтобы опровергнуть гипотезу, необходимо придумать алгоритм, который невозможно записать в виде программы для машины названной в честь автора данного тезиса. На сегодняшний день такого алгоритма не существует.
в) Согласно этому принципу класс функций,
вычислимых с помощью алгоритмов в широком интуитивном
смысле, совпадает с классом частично рекурсивных функций.
Данный тезис не может быть строго доказан, но считается
справедливым, поскольку он подтверждается опытом, накопленным в математике за всю ее историю. Какие бы классы алгоритмов ни строились, вычисляемые ими числовые функции оказывались частично рекурсивными.