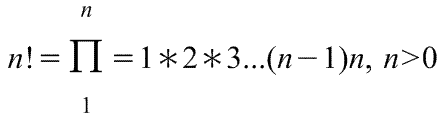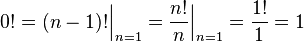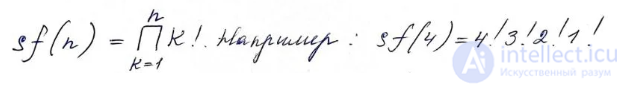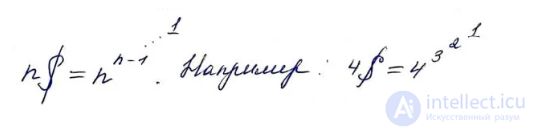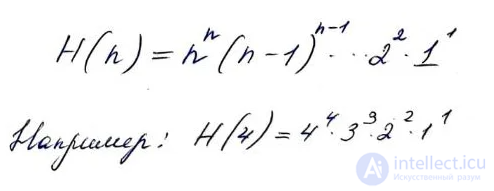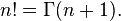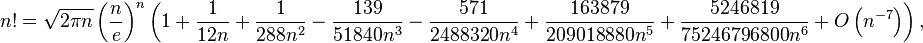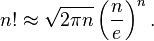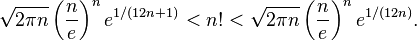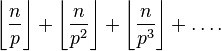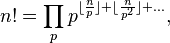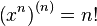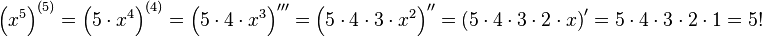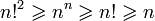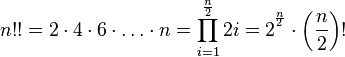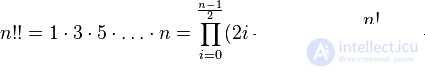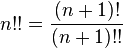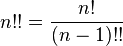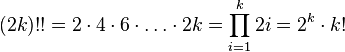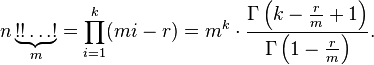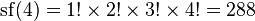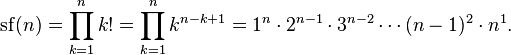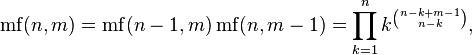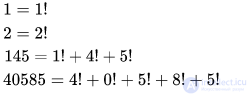Факториал что это
Факториал что это
Что такое факториал и зачем он нужен?
n! — произведение всех натуральных чисел от 1 до n включительно:
нужен для удобства записи таких произведений.
Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:
Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так [1]:
1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …
Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
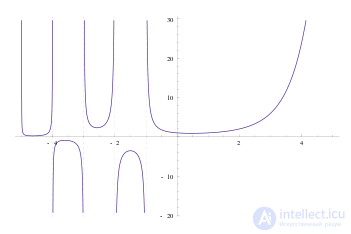
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества
ABCD BACD CABD DABC
ABDC BADC CADB DACB
ACBD BCAD CBAD DBAC
ACDB BCDA CBDA DBCA
ADBC BDAC CDAB DCAB
ADCB BDCA CDBA DCBA
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.
Связь с гамма-функцией [править | править вики-текст]
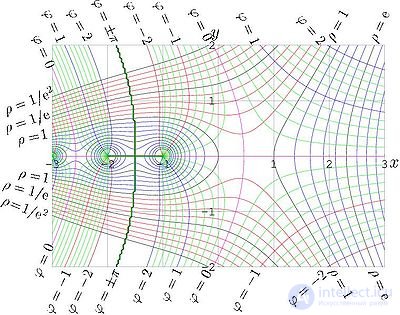
Амплитуда и фаза факториала комплексного аргумента.
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
.
Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению
Формула Стирлинга
Основная статья: Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое [2].
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
•100! ≈ 9,33×10157;
•1000! ≈ 4,02×102567;
•10 000! ≈ 2,85×1035 659.
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.
Связь с производной от степенной функции
Для целого неотрицательного числа n:
Другие свойства
•Для натурального числа n:
Обобщения
Двойной факториал
Запрос «‼» перенаправляется сюда; см. также другие значения.
Двойной факториал числа n о
Факториал
Смотреть что такое «Факториал» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
факториал
Смотреть что такое «факториал» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
ФАКТОРИАЛ
Полезное
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
Факториал
Смотреть что такое «Факториал» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
Значение слова «факториал»
По общепринятому соглашению,
Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако, степенно-показательная функция
растёт быстрее факториала, так же как и большинство двойных степенных, например
факториа́л
1. матем. произведение всех натуральных чисел от единицы до данного числа включительно ◆ Заметим мимоходом, что использование обозначений для факториалов и то, что в дальнейшем мы будем пользоваться некоторыми рассмотрениями, относящимися к конечным разностям, не выводит нас, по нашему мнению, за пределы наиболее простых положений алгебры. М. В. Остроградский, «Об одном вопросе, касающемся вероятностей извлечения», 1846 г. (цитата из НКРЯ) ◆ В немашинной математике иногда встречаются примеры определения функции через саму себя (классический пример ― факториал). В. А. Успенский, «Математическая логика в вычислительных науках и вычислительной практике», 2002 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова собачащий (прилагательное):
ФАКТОРИАЛ
Найдено 2 изображения:
факториал м. Произведение чисел натурального ряда от единицы до некоторого данного числа (в математике).
ФАКТОРИАЛ (англ. factorial, от factor-сомножитель) (матем.), произведение натуральных чисел от единицы до к.-л. данного натурального числа п, то есть l*2*. *n; обозначается n!. При больших п приближённое выражение Ф. даётся Стирлинга формулой. Ф. равен числу перестановок из п элементов.
Факториал — Ф. есть выражение вида х(х — h)(х — 2h). (х — nh). Здесь х и h могут иметь произвольные значения, a n есть целое положительное число. Такого рода выражения имеют большое значение в исчислении конечных разностей (см.). Для того, чтобы, напр., вычислить сумму f(1) + f(2) + f(3) +. + f(n), где f(x) целая функция от x, то сначала разлагают f(x) по Ф., а потом производят суммирование. Д. С.
факториал
Смотреть что такое «факториал» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas
Как факториалы используются в реальной жизни?
Это очень полезно, когда мы пытаемся подсчитайте, сколько существует различных заказов на вещи или сколько различных способов мы можем комбинировать вещи. Например, сколькими различными способами мы можем расположить n вещей? У нас есть n вариантов для первого.
Из этого следует, как вы произносите n factorial?
Для чего используются факториалы в математике? Факториал — это операция умножения любого натурального числа на все натуральные числа, которые меньше его, что дает нам математическое определение n! … Наконец, факториал используется для вопросы, которые просят вас выяснить, сколькими способами вы можете расположить или заказать определенное количество вещей.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Дополнительно Как решить 6 факториала?
Что является примером факториала? Факториалы (!) произведения каждого целого числа от 1 до n. Другими словами, возьмите число и умножьте его на 1. Например: если n равно 3, то 3! 3 х 2 х 1 = 6.
Сколько стоит факториал 100?
Количество цифр в факториале 100 равно 158.
Что такое факториал сотни? Число 100! (произносится как «сто факториал») — это число, которое получается при умножении всех целых чисел от 1 до 100. То есть 100! знак равно 1×2×3×… × 99 × 100.
Как сказать 10 3 по-английски?
Что такое пять как число?
| ← 4 5 6 → | |
|---|---|
| Кардинальный | 5 |
| порядковый | 5 (пятый) |
| Система счисления | пятеричный |
| факторизация | простое число |
Также как решить 5? Чтобы найти факториал 5 или 5!, просто используйте формулу; то есть перемножьте все целые числа от 5 до 1. Когда мы используем формулу для нахождения 5!, мы получаем 120. Итак, 5! = 120.
Фактиарное сложение или умножение?
Как быстро решать факториалы?
Можно ли умножать факториалы?
Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.
Что такое факторный план 3 × 4?
— числовые значения относятся к количеству уровней каждого фактора; 3 × 4 = 2 фактора, один с 3 уровнями и один с 4 уровнями.
Что такое факториал Anova 2 × 3? 2×3 = Есть два IV, первая IV имеет два уровня, вторая IV имеет три уровня. Всего имеется 6 условий, 2×3 = 6. 3×2 = Есть два IV, первый IV имеет три уровня, второй IV имеет два уровня.
Что такое факторный план 2 × 2? план эксперимента, в котором есть две независимые переменные, каждая из которых имеет два уровня. Когда этот план изображается в виде матрицы, две строки представляют одну из независимых переменных, а два столбца представляют другую независимую переменную.
Что такое факториал для 20?
Ответ: Факториал числа 20 равен 2432902008176640000.
Факториал n обозначается через n!
Каковы коэффициенты 100?
Коэффициенты 100 являются 1, 2, 4, 5, 10, 20, 25, 50 и 100.
Как вы читаете триллионы?
Как вы читаете полномочия?
Как вы читаете() по математике?
Что такое факториал?
Я думаю трудно найти человека, который не знал бы, что такое факториал. Но, чёрт возьми, такая красивая математическая операция, давайте поговорим о ней снова. Тем более постарался максимально доходчиво объяснить материал даже очень далеким от математики людям. Поехали!
Кто из Вас помнит, когда столкнулся с факториалом впервые? Я, например, абсолютно уверен, что первый раз увидел значок n! на советской микро-ЭВМ Электроника МК-71. Меня поразило, в первую очередь, как с помощью этой кнопки быстро переполняется буфер и выскакивает ошибка. Потом уже, начав изучать математику, удалось поближе познакомиться с этим зверем. Начнем с определения:
Лаконично и просто.
Факториал крут тем, насколько быстро возрастает его значение, и если 5! равен всего лишь 120, то 10! — уже 3 628 800, а, например, факториал 1000000 равен 8,263931688Е+5565708. Факториал возрастает быстрее чем экспонента и степенная функция и даже чем их произведение, но, однако уступает функции n в степени n.
Короткий пример вычисления факториала
Важное уточнение: 0! = 1, что следует из определения факториала.
Если взять первым красный шар, а затем найти варианты расположения остальных — получим 6 вариантов. Перебрав все 4 шара получим 24 = 1*2*3*4=4! Таким образом, количество перестановок во множестве равно факториалу количества его членов.
Во-вторых, факториал применяется при расчете количества размещений — еще одной операции из мира комбинаторики. Суть ее проста, поясним ее на всё том же примере разноцветных шаров. Ответьте на вопрос: сколько способов отдельного размещения 2 шаров из представленных 4 (разный порядок — разный способ) ?
Всего имеется 12 вариантов размещения 2 элементов из 4. То, что мы сейчас посчитали руками формализуется следующим образом через факториал:
Читается как количество размещений из n элементов по m
В-третьих, факториал присутствует в формуле количества сочетаний из n элементов по m. Сочетания отличаются от размещений тем, что если набор элементов одинаков — он не учитывается.
На рисунке обведены сочетания: как видно, их стало в 2 раза меньше. Формула вычисления количества сочетаний из n элементов по k выглядит так:
Раз уж мы разобрались с перестановками, размещениями и сочетаниями, перейдем к «имени нарицательному», страшному и пугающему: биному Ньютона. Как окажется, знание факториала и последней формулы легко позволит Вам расколоть этот «крепкий орешек».
Как ни странно, бином Ньютона это выражение (1+x)^n и его легко найти через формулу сочетаний (доказательство естественно опустим). Вот небольшой пример нахождения бинома третьей степени, который легко перепроверить перемножением.
Разобравшись с этим примером, можете спокойно спорить с друзьями и знакомыми, что без проблем вычислите бином Ньютона n-ной степени!
Некоторые интересные свойства факториала
Во многих случаев, когда не требуется точного вычисления факториала не требуется, можно воспользоваться формулой Стирлинга:
Например, реальное значение факториала 5 — это 120. По формуле Стирлинга получается так:
Строго говоря, это только первый член бесконечного ряда. С увеличением количества членом приближение будет всё точнее
Идем дальше. До этого мы условились, что в качестве подфакториальной переменной, рассматриваем только натуральные числа. А что, если бы нам захотелось вычислить факториал дробного числа? Оказывается, и такой факториал тоже существует.
Используются такие расчеты при статистическом описании нейронных сетей. Данные вычисления приближенные, чтобы точно вычислять значение таких факториалов, используется Гамма-функция. Но это уже совсем другая история.
Есть еще двойной факториал, обозначаемый n!!. Формула его вычисления зависит от четности или нечетности аргумента.
Думаю принцип понятен без дополнительных пояснений.
Кроме того, существует «король факториалов», так называемый суперфакториал, который равен произведению факториалов числа, меньше либо равного данному:
Ну а дальше пошло-поехало: придумали гиперфакториалы, которые равны произведениям суперфакториалов, а потом и вовсе обобщили в m-кратный факториал.
Вот еще несколько интересных свойств факториала и заканчиваем:
1) n! — никогда не является квадратом какого-либо числа.
Точная и приблизительная таблицы факториалов (1-255)
Точная и приблизительная таблицы факториалов (1-255)
Факториал n! произвольного целого числа n≥0 определяется по формуле:
Приблизительная таблица факториалов. (1-255)
| Факториал | Значение | Факториал | Значение | Факториал | Значение |
| 1! | 1 | 86! | 2,42*10 130 | 171! | 1,24*10 309 |
| 2! | 2 | 87! | 2,11*10 132 | 172! | 2,13*10 311 |
| 3! | 6 | 88! | 1,85*10 134 | 173! | 3,69*10 313 |
| 4! | 24 | 89! | 1,65*10 136 | 174! | 6,43*10 315 |
| 5! | 1,2*10 2 | 90! | 1,49*10 138 | 175! | 1,12*10 318 |
| 6! | 7,2*10 2 | 91! | 1,35*10 140 | 176! | 1,98*10 320 |
| 7! | 5,04*10 3 | 92! | 1,24*10 142 | 177! | 3,50*10 322 |
| 8! | 4,03*10 4 | 93! | 1,16*10 144 | 178! | 6,24*10 324 |
| 9! | 3,62*10 5 | 94! | 1,09*10 146 | 179! | 1,12*10 327 |
| 10! | 3,62*10 6 | 95! | 1,03*10 148 | 180! | 2,01*10 329 |
| 11! | 3,99*10 7 | 96! | 9,92*10 149 | 181! | 3,64*10 331 |
| 12! | 4,79 | 97! | 9,62*10 151 | 182! | 6,62*10 333 |
| 13! | 6,22*10 9 | 98! | 9,43*10 153 | 183! | 1,21*10 336 |
| 14! | 8,71*10 10 | 99! | 9,33*10 155 | 184! | 2,23*10 338 |
| 15! | 1,30*10 12 | 100! | 9,33*10 157 | 185! | 4,12*10 340 |
| 16! | 2,09*10 13 | 101! | 9,43*10 159 | 186! | 7,68*10 342 |
| 17! | 3,55*10 14 | 102! | 9,61*10 161 | 187! | 1,43*10 345 |
| 18! | 6,40*10 15 | 103! | 9,9*10 163 | 188! | 2,69*10 347 |
| 19! | 1,21*10 17 | 104! | 1,03*10 166 | 189! | 5,09*10 349 |
| 20! | 2,43*10 18 | 105! | 1,08*10 168 | 190! | 9,68*10 351 |
| 21! | 5,10*10 19 | 106! | 1,15*10 170 | 191! | 1,85*10 354 |
| 22! | 1,12*10 21 | 107! | 1,23*10 172 | 192! | 3,55*10 356 |
| 23! | 2,58*10 22 | 108! | 1,32*10 174 | 193! | 6,85*10 358 |
| 24! | 6,20*10 23 | 109! | 1,44*10 176 | 194! | 1,33*10 361 |
| 25! | 1,55*10 25 | 110! | 1,59*10 178 | 195! | 2,59*10 363 |
| 26! | 4,03*10 26 | 111! | 1,76*10 180 | 196! | 5,08*10 365 |
| 27! | 1,08*10 28 | 112! | 1,97*10 182 | 197! | 1,00*10 368 |
| 28! | 3,05*10 29 | 113! | 2,23*10 184 | 198! | 1,98*10 370 |
| 29! | 8,84*10 30 | 114! | 2,54*10 186 | 199! | 3,94*10 372 |
| 30! | 2,65*10 32 | 115! | 2,93*10 188 | 200! | 7,89*10 374 |
| 31! | 8,22*10 33 | 116! | 3,39*10 190 | 201! | 1,59*10 377 |
| 32! | 2,63*10 35 | 117! | 3,97*10 192 | 202! | 3,20*10 379 |
| 33! | 8,68*10 36 | 118! | 4,68*10 194 | 203! | 6,50*10 381 |
| 34! | 2,95*10 38 | 119! | 5,57*10 196 | 204! | 1,33*10 384 |
| 35! | 1,03*10 40 | 120! | 6,69*10 198 | 205! | 2,72*10 386 |
| 36! | 3,72*10 41 | 121! | 8,09*10 200 | 206! | 5,60*10 388 |
| 37! | 1,38*10 43 | 122! | 9,88*10 202 | 207! | 1,16*10 391 |
| 38! | 5,23*10 44 | 123! | 1,21*10 205 | 208! | 2,41*10 393 |
| 39! | 2,04*10 46 | 124! | 1,51*10 207 | 209! | 5,04*10 395 |
| 40! | 8,16*10 47 | 125! | 1,88*10 209 | 210! | 1,06*10 398 |
| 41! | 3,35*10 49 | 126! | 2,37*10 211 | 211! | 2,23*10 400 |
| 42! | 1,41*10 51 | 127! | 3,01*10 213 | 212! | 4,73*10 402 |
| 43! | 6,04*10 52 | 128! | 3,86*10 215 | 213! | 1,01*10 405 |
| 44! | 2,66*10 54 | 129! | 4,97*10 217 | 214! | 2,16*10 407 |
| 45! | 1,19*10 56 | 130! | 6,47*10 219 | 215! | 4,64*10 409 |
| 46! | 5,50*10 57 | 131! | 8,47*10 221 | 216! | 1,00*10 412 |
| 47! | 2,59*10 59 | 132! | 1,12*10 224 | 217! | 2,17*10 414 |
| 48! | 1,24*10 61 | 133! | 1,49*10 226 | 218! | 4,74*10 416 |
| 49! | 6,08*10 62 | 134! | 1,99*10 228 | 219! | 1,04*10 419 |
| 50! | 3,04*10 64 | 135! | 2,69*10 230 | 220! | 2,28*10 421 |
| 51! | 1,55*10 66 | 136! | 3,66*10 232 | 221! | 5,04*10 423 |
| 52! | 8,07*10 67 | 137! | 5,01*10 234 | 222! | 1,12*10 426 |
| 53! | 4,28*10 69 | 138! | 6,92*10 236 | 223! | 2,50*10 428 |
| 54! | 2,31*10 71 | 139! | 9,62*10 238 | 224! | 5,60*10 430 |
| 55! | 1,27*10 73 | 140! | 1,35*10 241 | 225! | 1,30*10 433 |
| 56! | 7,11*10 74 | 141! | 1,90*10 243 | 226! | 2,85*10 435 |
| 57! | 4,05*10 76 | 142! | 2,7*10 245 | 227! | 6,46*10 437 |
| 58! | 2,35*10 78 | 143! | 3,85*10 247 | 228! | 1,47*10 440 |
| 59! | 1,39*10 80 | 144! | 5,55*10 249 | 229! | 3,37*10 442 |
| 60! | 8,32*10 81 | 145! | 8,05*10 251 | 230! | 7,76*10 444 |
| 61! | 5,08*10 83 | 146! | 1,17*10 254 | 231! | 1,79*10 447 |
| 62! | 3,15*10 85 | 147! | 1,73*10 256 | 232! | 4,16*10 449 |
| 63! | 1,98*10 87 | 148! | 2,56*10 258 | 233! | 9,69*10 451 |
| 64! | 1,27*10 89 | 149! | 3,81*10 260 | 234! | 2,67*10 454 |
| 65! | 8,25*10 90 | 150! | 5,71*10 262 | 235! | 5,33*10 456 |
| 66! | 5,44*10 92 | 151! | 8,63*10 264 | 236! | 1,26*10 459 |
| 67! | 3,65*10 94 | 152! | 1,31*10 267 | 237! | 2,98*10 461 |
| 68! | 2,48*10 96 | 153! | 2,01*10 269 | 238! | 7,09*10 463 |
| 69! | 1,71*10 98 | 154! | 3,09*10 271 | 239! | 1,70*10 466 |
| 70! | 1,20*10 100 | 155! | 4,79*10 273 | 240! | 4,07*10 468 |
| 71! | 8,50*10 101 | 156! | 7,47*10 275 | 241! | 9,80*10 470 |
| 72! | 6,12*10 103 | 157! | 1,17*10 278 | 242! | 2,37*10 473 |
| 73! | 4,47*10 105 | 158! | 1,85*10 280 | 243! | 5,77*10 475 |
| 74! | 3,31*10 107 | 159! | 2,95*10 282 | 244! | 1,41*10 478 |
| 75! | 2,48*10 109 | 160! | 4,71*10 284 | 245! | 3,45*10 480 |
| 76! | 1,89*10 111 | 161! | 7,59*10 286 | 246! | 8,48*10 482 |
| 77! | 1,45*10 113 | 162! | 1,23*10 289 | 247! | 2,09*10 485 |
| 78! | 1,13*10 115 | 163! | 2,00*10 291 | 248! | 5,19*10 487 |
| 79! | 8,95*10 116 | 164! | 3,29*10 293 | 249! | 1,29*10 490 |
| 80! | 7,16*10 118 | 165! | 5,42*10 295 | 250! | 3,23*10 492 |
| 81! | 5,80*10 120 | 166! | 9,00*10 297 | 251! | 8,11*10 494 |
| 82! | 4,75*10 122 | 167! | 1,50*10 300 | 252! | 2,04*10 497 |
| 83! | 3,95*10 124 | 168! | 2,53*10 302 | 253! | 5,17*10 499 |
| 84! | 3,31*10 126 | 169! | 4,27*10 304 | 254! | 1,31*10 502 |
| 85! | 2,82*10 128 | 170! | 7,26*10 306 | 255! | 3,35*10 504 |
Точная таблица факториалов (1-255)
Факториал
Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
| 11 | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
| 14 | 87 178 291 200 |
| 15 | 1 307 674 368 000 |
| 16 | 20 922 789 888 000 |
| 17 | 355 687 428 096 000 |
| 18 | 6 402 373 705 728 000 |
| 19 | 121 645 100 408 832 000 |
| 20 | 2 432 902 008 176 640 000 |
| 25 | ≈ 1,551121004 × 10 25 |
| 50 | ≈ 3,041409320 × 10 64 |
| 70 | ≈ 1,197857167 × 10 100 |
| 100 | ≈ 9,332621544 × 10 157 |
| 450 | ≈ 1,733368733 × 10 1000 |
| 1 000 | ≈ 4,023872601 × 10 2567 |
| 3 249 | ≈ 6,412337688 × 10 10000 |
| 10 000 | ≈ 2,846259681 × 10 35659 |
| 25 206 | ≈ 1,205703438 × 10 100000 |
| 100 000 | ≈ 2,824229408 × 10 456573 |
| 205 023 | ≈ 2,503898932 × 10 1000004 |
| 1 000 000 | ≈ 8,263931688 × 10 5565708 |
| 10 100 | ≈10 9,956570552 × 10 101 |
| 10 1000 | ≈10 10 1003 |
| 10 10 000 | ≈10 10 10 004 |
| 10 100 000 | ≈10 10 100 005 |
| 10 10 100 | ≈10 10 10 100 |
Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако, степенно-показательная функция n n <\displaystyle n^
растёт быстрее факториала, так же как и большинство двойных степенных, например e e n <\displaystyle e^.
Содержание
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества <A,B,C,D> из 4-х элементов существует 4! = 24 перестановки:
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением
Π ( z ) = ∫ 0 ∞ t z e − t d t <\displaystyle \Pi (z)=\int _<0>^<\infty >t^(интегральное определение).
Формула Стирлинга
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
Связь с производной от степенной функции
Для целого неотрицательного числа n :
Другие свойства
История
Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:
Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение [4] :
Развивая эту идею, Эйлер в следующем, 1730 году ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Санкт-Петербургской Академии наук в 1729—1730 годах.
Обобщения
Двойной факториал
Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
Пример, иллюстрирующий использованное выше выведение формулы:
Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.
Последовательность значений n!! начинается так [5] :
1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …
Кратный факториал
Кратный факториал связан с гамма-функцией следующим соотношением [7] :
Неполный факториал
Убывающий факториал
Убывающим факториалом называется выражение
n = 7; k = 4, ( n − k ) + 1 = 4, n k = 7 • 6 • 5 • 4 = 840.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Праймориал или примориал (англ. primorial ) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например,
p 5 # = 2 × 3 × 5 × 7 × 11 = 2310 <\displaystyle p_<5>\#=2\times 3\times 5\times 7\times 11=2310> .
Последовательность праймориалов (включая 1 # ≡ 1 <\displaystyle <\textstyle <1\#\equiv 1>>> ) начинается так [8] :
1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, …
Суперфакториалы
Нейл Слоан и Симон Плуффэ ( англ. ) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен
(поскольку устоявшегося обозначения нет, используется функциональное).
1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000, …
1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000, …
Субфакториал
Факториал
n! = 1\cdot 2\cdot\ldots\cdot n =\prod_
Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так [1] :
1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция e^
Содержание
Свойства
Рекуррентная формула
1 & n = 0,\\ n \cdot (n-1)! & n > 0. \end
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества <A,B,C,D> из 4-х элементов существует 4! = 24 перестановки:
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
Поскольку \Pi(z) = \Gamma(z+1) \,, то пи-функция натурального числа совпадает с его факториалом: \Pi(n) = n!. Как факториал, пи-функция удовлетворяет рекурсивному соотношению \Pi(z) = z\Pi(z-1)\,.
Формула Стирлинга
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
\left\lfloor \frac
\right\rfloor + \left\lfloor \frac
Связь с производной от степенной функции
Для целого неотрицательного числа n :
= \left( 5 \cdot x^4 \right)^ <(4)>= \left( 5 \cdot 4 \cdot x^3 \right) = \left( 5 \cdot 4 \cdot 3 \cdot x^2 \right) = \left( 5 \cdot 4 \cdot 3 \cdot 2 \cdot x \right)’ = <5 \cdot 4 \cdot 3 \cdot 2 \cdot 1>= 5!
Другие свойства
Обобщения
Двойной факториал
Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
Пример, иллюстрирующий использованное выше выведение формулы: \begin
\\ & = (2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2) \cdot (1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7) = \\ & = (2 \cdot 1) (2 \cdot 2) (2 \cdot 3) (2 \cdot 4) (2 \cdot 5) (2 \cdot 6) (2 \cdot 7) = \\ & = 2 \cdot 4 \cdot 6 \cdot 8 \cdot 10 \cdot 12 \cdot 14 = 645120 \end
Подставим полученное выражение для знаменателя обратно в формулу для n!! : n!! = \frac Пример, иллюстрирующий использованное выше выведение формулы: Осуществив замену n=2k для чётного n и n=2k+1 для нечётного n соответственно, где k — целое неотрицательное число, получим: 0!! = 2^0 \cdot 0! = 1 \cdot 1 = 1 Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел. Последовательность значений n!! начинается так [4] : 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … Кратный факториал связан с гамма-функцией следующим соотношением [6] : Убывающим факториалом называется выражение n = 7; k = 4, ( n − k ) + 1 = 4, n k = 7 • 6 • 5 • 4 = 840. Возрастающим факториалом называется выражение Праймориал или примориал (англ. primorial ) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например, Последовательность праймориалов (включая <\textstyle<1\# \equiv 1>> ) начинается так [7] : 1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … Нейл Слоан и Симон Плуффэ (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен \operatorname (поскольку устоявшегося обозначения нет, используется функциональное). Последовательность суперфакториалов чисел n \geqslant 0 начинается так [8] : 1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000, … Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial ), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n \geqslant 0 начинается так [9] : 1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000, … где \operatorname : неверное или отсутствующее изображение – Молодцы! – сказал, смеясь, Ростов. – Что, сено есть? Ростов, не желая навязывать свое знакомство княжне, не пошел к ней, а остался в деревне, ожидая ее выезда. Дождавшись выезда экипажей княжны Марьи из дома, Ростов сел верхом и до пути, занятого нашими войсками, в двенадцати верстах от Богучарова, верхом провожал ее. В Янкове, на постоялом дворе, он простился с нею почтительно, в первый раз позволив себе поцеловать ее руку. ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1. ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas Было определено много функций, аналогичных факториальной функции ; на этой странице перечислены наиболее часто встречающиеся варианты. Чтобы упростить написание, обычная нотация заключается в использовании q восклицательных знаков после числа n для обозначения этой функции. Некоторые идентичности вытекают из определения: Нил Слоан и Саймон Плафф определили суперфакториал в 1995 году как произведение первых n факториалов: Например, суперфакториал 4 равен: Последовательность из superfactorials начинается (от SF (0) = 1 ) с: Первыми элементами последовательности суперфакториалов являются: Например, есть! n способ вложить n писем в n конвертов с указанием адресов и адресов, чтобы ни одна из писем не оказалась в правильном конверте. Есть разные способы расчета субфакториала Первые значения этой функции: Последовательность fibonariels является эквивалентом в зависимости от золотого отношения ф : ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas Большой современный толковый словарь русского языка Новый словарь иностранных слов м. Произведение чисел натурального ряда от единицы до некоторого данного числа (в математике). Новый толково-словообразовательный словарь русского языка Ефремовой Словарь иностранных выражений произведение натуральных чисел от единицы до какого-либо данного натурального числа n, т. е. 1·2·3·… ·n; обозначается n!. Напр., 5! = 1·2·3·4·5 = Современный толковый словарь, БСЭ факториал м. Произведение чисел натурального ряда от единицы до некоторого данного числа (в математике). Толковый словарь Ефремовой Большая советская энциклопедия, БСЭ Полный орфографический словарь русского языка произведение всех натуральных чисел от единицы до данного числа включительно Прошло пять лет, прежде чем мы смогли продвинуться дальше элементарных арифметических примеров: три плюс четыре равно семи, корень квадратный из двадцати пяти равен пяти, шесть факториал равен семистам двадцати. Каждый из них может быть прочтен как слово: «плюс» или «прибавить», «минус» или «отнять»; « факториал » или «произведение всех чисел от единицы до данного числа» (5! — это произведение 1X2X3X4X5 и т. п.), «равно» или «равняется». Поэтому она перепутала факториал с одним из видов арифметической прогрессии — суммой натуральных чисел. Когда персонажи обеих девочек начали обсуждать проблемы современного детектива, то тамагочи Single утверждал, что факториал заключает в себе положительное начало, а питомец Сони готовит Апокалипсис отстаивал противоположную точку зрения, мотивируя тем, что во многих детективах действие происходит в игорных домах, в частности в Лас-Вегасе, а сумма натуральных чисел от 1 до 36, используемая в рулетке, является мистическим числом 666. факториал числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральныхчисел от 1 до n включительно: По договоренности: Факториал определен только для целых неотрицательных чисел. Последовательность факториалов неотрицательных целых чисел начинается так: Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе. Факториал является чрезвычайно быстро растущей функцией. Он растет быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция В математике существует около десятка различных факториалов, рассмотрим их пример 5! = 1*2*3*4*5 Этот факториал имеет просто громадное количество приложений в комбинаторике и достоин отдельного материала. Впервые он использовался при выводе замечательного произведения Уоллиса, связывающего натуральные числа и число π: Этот представитель семейства в отличие от обычного факториала, который определяет количество перестановок, определяет количество беспорядков. Определяется как произведение простых чисел, меньших или равных данному. Название дано создателем уникальной в своем роде Онлайн Энциклопедии Целочисленных Последовательностей (OEIS). Определяется как произведение факториалов чисел, меньших или равных заданному. Растет еще медленнее, чем предшествующие два. Только лишь на 14 шаге число нулей приближается к гуголу. Равняется произведению первых n чисел Фибоначчи. А также факториал дробного числа. Вычисляется по формуле: где [x] — целая часть чиcла x, Например, для x=11,2 будем иметь log(11,2!) = log(11!) + 0,2*log(12) Вычисляемое таким способом значение факториала дробного числа является приближенным. Для точных расчетов необходимо использовать гамма-функцию. Факториалы нецелых (дробных) чисел появляются при статистическом описании нейросетевых преобразователей биометрия/код ключа доступа биномиальным законом распределения зависмимых биометрических данных. 0. \end В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества <A,B,C,D> из 4-х элементов существует 4! = 24 перестановки: Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом. Амплитуда и фаза факториала комплексного аргумента. Факториал связан с гамма-функцией от целочисленного аргумента соотношением: Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путем аналитического продолжения ее также расширяют и на всю комплексную плоскость, исключаяособые точки при Пи-функция, определенная для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом. Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как Поскольку Формула Стирлинга Формула Стирлинга — асимптотическая формула для вычисления факториала: Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга: При этом можно утверждать, что Формула Стирлинга позволяет получить приближенные значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что Каждое простое число p входит в разложение n! на простые множители в степени где произведение берется по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n. Для целого неотрицательного числа n: Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же четность, что и n. Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них. Осуществив замену По договоренности: Двойной факториал, также как и обычный факториал, определен только для целых неотрицательных чисел. Последовательность значений n!! начинается так: m-кратный факториал числа n обозначается Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно. Кратный факториал связан с гамма-функцией следующим соотношением : Убывающим факториалом называется выражение 3k = 7 • 6 • 5 • 4 = 840. Убывающий факториал дает число размещений из n по k. Возрастающим факториалом называется выражение Сюда перенаправляется запрос «Праймориал». На эту тему нужна отдельная статья. Праймориал или примориал (англ. primorial) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например, Иногда праймориалом называют число Последовательность праймориалов (включая Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырех равен (поскольку устоявшегося обозначения нет, используется функциональное). Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых nсуперфакториалов. Последовательность гиперфакториалов чисел Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть где Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок. В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (так называемая Задача о письмах). «Примеры реализации функции факториал» Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала. Это очень просто, вот пример: 7! = 1 * … * 7 = 5040. Факторизация — разложение функции на множители. \frac<15!><2^<<\color
Кратный факториал
Неполный факториал
Убывающий факториал
Возрастающий факториал
Праймориал или примориал
Суперфакториалы
Субфакториал
См. также
Напишите отзыв о статье «Факториал»
Примечания
Отрывок, характеризующий Факториал
– И одинакие какие… – сказал Ильин.
– Развесе…oo…ооо…лая бесе… бесе… – распевали мужики с счастливыми улыбками.
Один мужик вышел из толпы и подошел к Ростову.
– Вы из каких будете? – спросил он.
– Французы, – отвечал, смеючись, Ильин. – Вот и Наполеон сам, – сказал он, указывая на Лаврушку.
– Стало быть, русские будете? – переспросил мужик.
– А много вашей силы тут? – спросил другой небольшой мужик, подходя к ним.
– Много, много, – отвечал Ростов. – Да вы что ж собрались тут? – прибавил он. – Праздник, что ль?
– Старички собрались, по мирскому делу, – отвечал мужик, отходя от него.
В это время по дороге от барского дома показались две женщины и человек в белой шляпе, шедшие к офицерам.
– В розовом моя, чур не отбивать! – сказал Ильин, заметив решительно подвигавшуюся к нему Дуняшу.
– Наша будет! – подмигнув, сказал Ильину Лаврушка.
– Что, моя красавица, нужно? – сказал Ильин, улыбаясь.
– Княжна приказали узнать, какого вы полка и ваши фамилии?
– Это граф Ростов, эскадронный командир, а я ваш покорный слуга.
– Бе…се…е…ду…шка! – распевал пьяный мужик, счастливо улыбаясь и глядя на Ильина, разговаривающего с девушкой. Вслед за Дуняшей подошел к Ростову Алпатыч, еще издали сняв свою шляпу.
– Осмелюсь обеспокоить, ваше благородие, – сказал он с почтительностью, но с относительным пренебрежением к юности этого офицера и заложив руку за пазуху. – Моя госпожа, дочь скончавшегося сего пятнадцатого числа генерал аншефа князя Николая Андреевича Болконского, находясь в затруднении по случаю невежества этих лиц, – он указал на мужиков, – просит вас пожаловать… не угодно ли будет, – с грустной улыбкой сказал Алпатыч, – отъехать несколько, а то не так удобно при… – Алпатыч указал на двух мужиков, которые сзади так и носились около него, как слепни около лошади.
– А. Алпатыч… А? Яков Алпатыч. Важно! прости ради Христа. Важно! А. – говорили мужики, радостно улыбаясь ему. Ростов посмотрел на пьяных стариков и улыбнулся.
– Или, может, это утешает ваше сиятельство? – сказал Яков Алпатыч с степенным видом, не заложенной за пазуху рукой указывая на стариков.
– Нет, тут утешенья мало, – сказал Ростов и отъехал. – В чем дело? – спросил он.
– Осмелюсь доложить вашему сиятельству, что грубый народ здешний не желает выпустить госпожу из имения и угрожает отпречь лошадей, так что с утра все уложено и ее сиятельство не могут выехать.
– Не может быть! – вскрикнул Ростов.
– Имею честь докладывать вам сущую правду, – повторил Алпатыч.
Ростов слез с лошади и, передав ее вестовому, пошел с Алпатычем к дому, расспрашивая его о подробностях дела. Действительно, вчерашнее предложение княжны мужикам хлеба, ее объяснение с Дроном и с сходкою так испортили дело, что Дрон окончательно сдал ключи, присоединился к мужикам и не являлся по требованию Алпатыча и что поутру, когда княжна велела закладывать, чтобы ехать, мужики вышли большой толпой к амбару и выслали сказать, что они не выпустят княжны из деревни, что есть приказ, чтобы не вывозиться, и они выпрягут лошадей. Алпатыч выходил к ним, усовещивая их, но ему отвечали (больше всех говорил Карп; Дрон не показывался из толпы), что княжну нельзя выпустить, что на то приказ есть; а что пускай княжна остается, и они по старому будут служить ей и во всем повиноваться.
В ту минуту, когда Ростов и Ильин проскакали по дороге, княжна Марья, несмотря на отговариванье Алпатыча, няни и девушек, велела закладывать и хотела ехать; но, увидав проскакавших кавалеристов, их приняли за французов, кучера разбежались, и в доме поднялся плач женщин.
– Батюшка! отец родной! бог тебя послал, – говорили умиленные голоса, в то время как Ростов проходил через переднюю.
Княжна Марья, потерянная и бессильная, сидела в зале, в то время как к ней ввели Ростова. Она не понимала, кто он, и зачем он, и что с нею будет. Увидав его русское лицо и по входу его и первым сказанным словам признав его за человека своего круга, она взглянула на него своим глубоким и лучистым взглядом и начала говорить обрывавшимся и дрожавшим от волнения голосом. Ростову тотчас же представилось что то романическое в этой встрече. «Беззащитная, убитая горем девушка, одна, оставленная на произвол грубых, бунтующих мужиков! И какая то странная судьба натолкнула меня сюда! – думал Ростов, слушяя ее и глядя на нее. – И какая кротость, благородство в ее чертах и в выражении! – думал он, слушая ее робкий рассказ.
Когда она заговорила о том, что все это случилось на другой день после похорон отца, ее голос задрожал. Она отвернулась и потом, как бы боясь, чтобы Ростов не принял ее слова за желание разжалобить его, вопросительно испуганно взглянула на него. У Ростова слезы стояли в глазах. Княжна Марья заметила это и благодарно посмотрела на Ростова тем своим лучистым взглядом, который заставлял забывать некрасивость ее лица.
– Не могу выразить, княжна, как я счастлив тем, что я случайно заехал сюда и буду в состоянии показать вам свою готовность, – сказал Ростов, вставая. – Извольте ехать, и я отвечаю вам своей честью, что ни один человек не посмеет сделать вам неприятность, ежели вы мне только позволите конвоировать вас, – и, почтительно поклонившись, как кланяются дамам царской крови, он направился к двери.
Почтительностью своего тона Ростов как будто показывал, что, несмотря на то, что он за счастье бы счел свое знакомство с нею, он не хотел пользоваться случаем ее несчастия для сближения с нею.
Княжна Марья поняла и оценила этот тон.
– Я очень, очень благодарна вам, – сказала ему княжна по французски, – но надеюсь, что все это было только недоразуменье и что никто не виноват в том. – Княжна вдруг заплакала. – Извините меня, – сказала она.
Ростов, нахмурившись, еще раз низко поклонился и вышел из комнаты.
– Как вам не совестно, – краснея, отвечал он княжне Марье на выражение благодарности за ее спасенье (как она называла его поступок), – каждый становой сделал бы то же. Если бы нам только приходилось воевать с мужиками, мы бы не допустили так далеко неприятеля, – говорил он, стыдясь чего то и стараясь переменить разговор. – Я счастлив только, что имел случай познакомиться с вами. Прощайте, княжна, желаю вам счастия и утешения и желаю встретиться с вами при более счастливых условиях. Ежели вы не хотите заставить краснеть меня, пожалуйста, не благодарите.
Но княжна, если не благодарила более словами, благодарила его всем выражением своего сиявшего благодарностью и нежностью лица. Она не могла верить ему, что ей не за что благодарить его. Напротив, для нее несомненно было то, что ежели бы его не было, то она, наверное, должна была бы погибнуть и от бунтовщиков и от французов; что он, для того чтобы спасти ее, подвергал себя самым очевидным и страшным опасностям; и еще несомненнее было то, что он был человек с высокой и благородной душой, который умел понять ее положение и горе. Его добрые и честные глаза с выступившими на них слезами, в то время как она сама, заплакав, говорила с ним о своей потере, не выходили из ее воображения.ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
Факториал
Смотреть что такое «Факториал» в других словарях:
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
Аналоги факториала
Резюме
Первобытный
Многофакторный
Двойной факториал
Многофакторность высшего порядка
Комбинаторные интерпретации
Гиперфакторный
Сверхфакторный
Суперфакториал (альтернативное определение)
Субфакторный
Факториал Фибоначчи
Экспоненциальный факториал
ФАКТОРИАЛ
Смотреть что такое «ФАКТОРИАЛ» в других словарях:
Значение слова факториал
Факториал в словаре кроссвордиста
факториал
Факториал Суперфакториалы гиперфакториал примориал
.
. Также это равенство выполняется естественным образом:
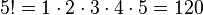
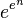
).1. Факториал
2. Двойной факториал
3. Субфакториал
4. Праймориал
5. суперфакториал Слоуна
6. Суперфакториал Пиковера
7. Экспоненциальный факториал
8. гиперфакториал
9. Фиббоначиал
10. Другие факториалы
История факториала
Свойства факториала
Рекуррентная формула
Комбинаторная интерпретация
Связь с гамма-функцией
.
.
то пи-функция натурального числа совпадает с его факториалом: 
Как факториал, пи-функция удовлетворяет рекурсивному соотношению 
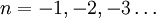
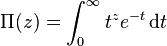
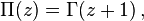
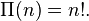
Формула Стирлинга
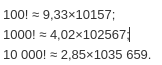
Разложение на простые числа
Связь с производной от степенной функции
Другие свойства
Обобщения
Двойной факториал
для четного n и 
для нечетного n соответственно, где 
— целое неотрицательное число, получим:
. Также это равенство выполняется естественным образом:
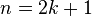
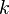
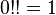
Кратный факториал
и определяется следующим образом. Пусть число n представимо в виде 
где 
Тогда
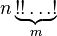
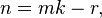
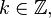
Неполный факториал
.
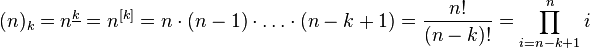
Праймориал или примориал
.
, определяемое как произведение всех простых чисел, не превышающих заданное n.
) начинается так:Суперфакториалы
начинается так:
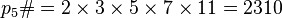
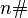
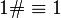
для 0″ src=»https://intellect.icu/th/25/blogs/id4266/50_3a17f57d9af78403b7ac2dd5f82c2d3c.png» / data-auto-open loading=»lazy» alt=»Факториал Суперфакториалы гиперфакториал примориал»> и 
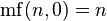
Субфакториал
Примечания
Факториал определение, формула, обозначение, основные свойства и функции, таблица, алгоритмы нахождения, примеры задач с решениями, онлайн-калькулятор
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).
| п | п! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
| 11 | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
| 14 | 87 178 291 200 |
| 15 | 1 307 674 368 000 |
| 16 | 20 922 789 888 000 |
| 17 | 355 687 428 096 000 |
| 18 | 6 402 373 705 728 000 |
| 19 | 121 645 100 408 832 000 |
| 20 | 2 432 902 008 176 640 000 |
| 25 | 1.551 121 004 × 10 25 |
| 50 | 3.041 409 320 × 10 64 |
| 70 | 1.197 857 167 × 10 100 |
| 100 | 9.332 621 544 × 10 157 |
| 450 | 1.733 368 733 × 10 1 000 |
| 1 000 | 4.023 872 601 × 10 2 567 |
| 3 249 | 6.412 337 688 × 10 10 000 |
| 10 000 | 2.846 259 681 × 10 35 659 |
| 25 206 | 1.205 703 438 × 10 100 000 |
| 100 000 | 2.824 229 408 × 10 456 573 |
| 205 023 | 2.503 898 932 × 10 1 000 004 |
| 1 000 000 | 8.263 931 688 × 10 5 565 708 |
| 10 100 | 10 10 101.998 109 775 4820 |
Значение 0! равно 1, согласно соглашению для пустой продукт. [1]
