Фибоначчи что это такое простыми словами

29.08.202229.08.2022 admin 0 Комментариев

Фибоначчи что это такое простыми словами

Число Фибоначчи. Почему оно так популярно в природе?

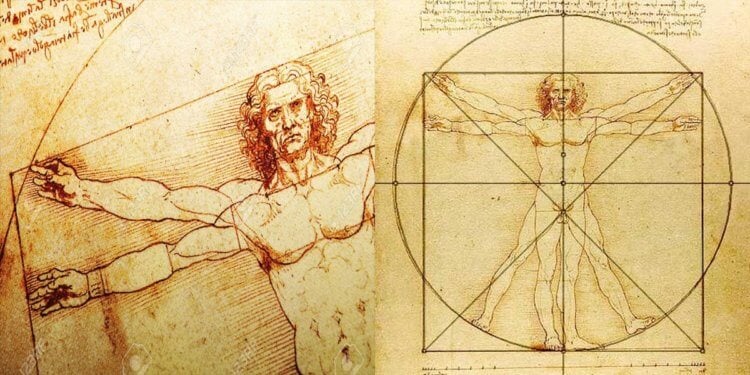
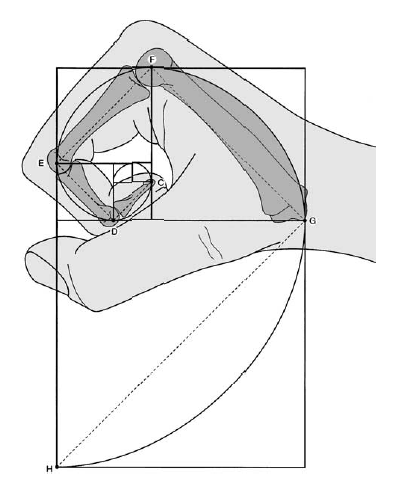
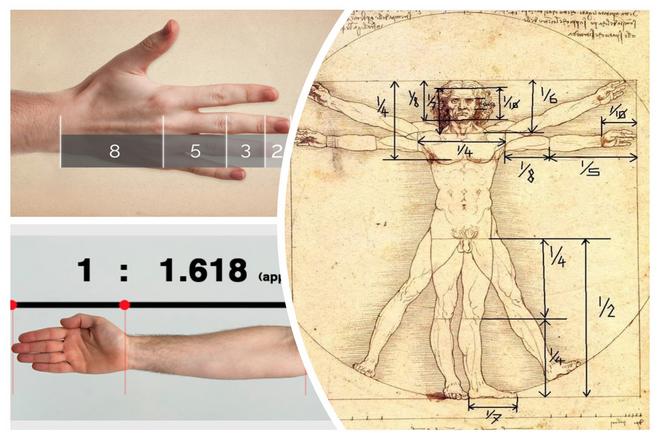
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.

«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи

Кто такой Фибоначчи?

Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.

В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.

Последовательность Фибоначчи

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

Где используется число Фибоначчи

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

Что такое золотое сечение

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.

Так выглядит «золотое сечение»

Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

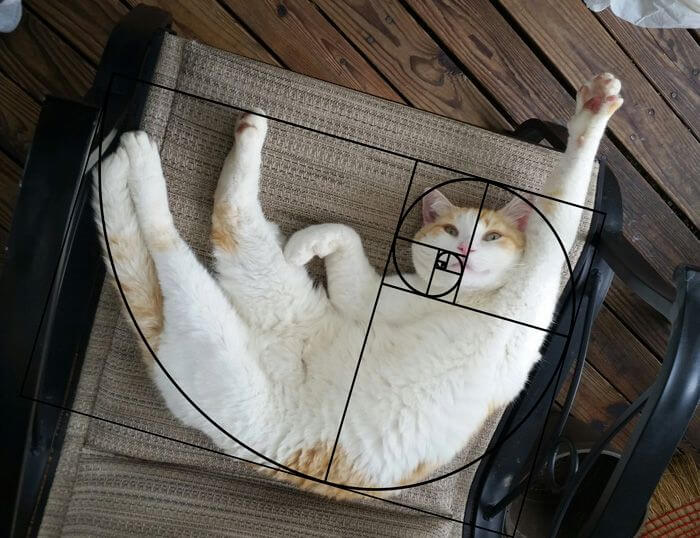
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

Новости, статьи и анонсы публикаций

Свободное общение и обсуждение материалов

Мы по-прежнему одиноки во Вселенной, и загадка парадокса Ферми ну никак не хочет решаться. Тем временем внутри научного сообщества зародилась новая гипотеза,…

Чтобы выжить, всем живым организмам нужно трудиться. Люди ходят на работу, чтобы иметь крышу над головой, а также чтобы не умереть от голода и скуки. Муравьи…

Когда мы смотрим на Вселенную, довольно трудно представить, что это вот все — планеты, звезды, галактики, сложные жизни, которыми мы наслаждаемся, — все возн…

Источник

Числа Фибоначчи

Числа Фибоначчи (строка Фибоначчи) — числовая последовательность, первые два числа которой являются 0 и 1, а каждое последующее за ними число является суммой двух предыдущих. Представляет собой частный пример линейной рекуррентной последовательности (рекурсии).

Эту последовательность впервые описал итальянский математик Леонардо Пизанский в его работе «Жизнь абака» в 1202 году. Закономерность, описываемая числами Фибоначчи, приобрела популярность в эпоху Возрождения и особенно Нового времени, где повлияла на самые разные стороны жизни — от фундаментальной и прикладной математики до искусства и архитектуры.

Описание чисел Фибоначчи

Сам Леонардо Пизанский (Фибоначчи — его прозвище) предложил знаменитую последовательность в виде «задачи о кроликах», где описал кроличью популяцию со следующими условиями:

Задача состояла в том, чтобы рассчитать, сколько кроликов в популяции будет через год. Математически ее решение описывается формулой:

Fn = Fn–2 + Fn–1, где F0=0, F1=1, а n — больше или равно 2 и является целым числом.

Рассчитанная по этой формуле последовательность выглядит так:

Сам Фибоначчи рассматривал эту последовательность просто как одно из математических упражнений среди прочих задач, указанных в его книге «Жизнь абака». Пример с кроликами был идеальной моделью, в которой кролики размножались строго каждый месяц, производили только двух крольчат разного пола и при этом сами не умирали. Однако некоторые современные исследователи называют ее первой в истории популяционной моделью.

Сама последовательность была известна еще с древних времен — в частности, она использовалась в древнеиндийском стихосложении, в том или ином виде ее знали древнегреческие и арабские математики. Заслуга именно Фибоначчи была в том, что он популяризировал ее в западноевропейской математике, а также ввел в европейскую науку позиционную систему счисления (известную народам Востока), которая имела краеугольное значение в последующем развитии математических наук.

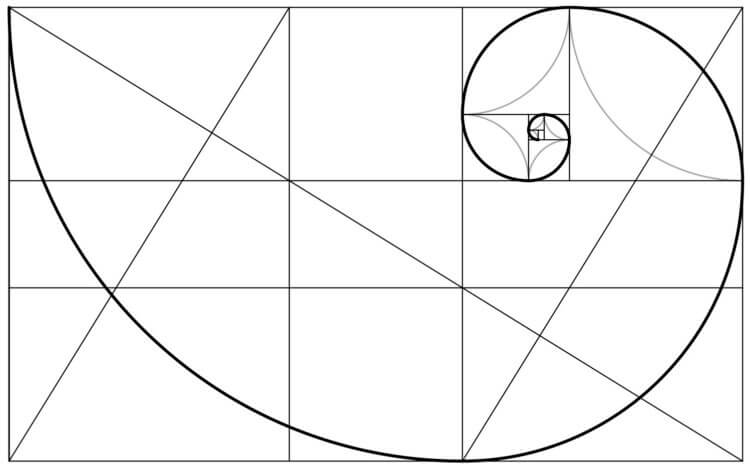
Визуальным воплощением этой последовательности является золотая спираль. Она представляет собой дуги окружностей, вписанных в квадраты, размеры которых соотносятся друг с другом как числа в строке Фибоначчи. В основе этой фигуры лежит золотое сечение — идеальная пропорция, равная 0,61803. Золотая спираль стала одним из распространенных принципов математического пропорционирования, который широко используется в искусстве, архитектуре, начиная с эпохи Возрождения и по сегодняшний день.

Применение рядов Фибоначчи в информатике и программировании

Последовательность Фибоначчи — один из классических примеров рекурсии в математике. Рекурсией называется функция, определяющая свое значение через обращение к самой себе. Рекурсивные алгоритмы используются в программировании для упрощения вычислений. Умение обращаться с ними является одним из базовых навыков программиста. Поэтому расчет числа Фибоначчи (достаточно простой рекуррентной функции) часто является тестовым заданием, которое дается соискателю на вакансию программиста для проверки его навыков или применяется в обучении будущих кодеров.

Например, так выглядит рекурсивный поиск чисел Фибоначчи на языке Python:

def fibonacci(n):
if n in (1, 2):
return 1
return fibonacci(n — 1) + fibonacci(n — 2)
print (fibonacci(10))

Проблема рекурсивного нахождения чисел Фибоначчи в том, что после определенного предела процесс сильно замедляется. Причина — в самой природе рекурсии: основанная на ней программа постоянно обращается сама к себе. Если число n (номер искомого элемента ряда) большое, обычный компьютер просто не справится или процесс займет слишком много времени.

Поэтому для нахождения чисел Фибоначчи применяются и другие способы — например, обычный цикл (язык Python):

Последовательность Фибоначчи и генерация псевдослучайных чисел

Случайными называются числа, полученные в результате случайного события. Простейший пример — подбрасывание монетки или игральной кости. Такие числовые последовательности широко используются в современной науке, например для описания различных природных, социальных, экономических и других процессов с влиянием большого количества различных факторов, делающих результаты трудно- или непредсказуемыми.

Проблема в том, что получить настоящие случайные числа очень сложно. Классические примеры с монеткой, игральными костями и колодой карт дают лишь небольшие величины, чего недостаточно для современной науки и технологий. Теоретически случайные числа можно получить из космического излучения или радиации, из дробового шума в электрических цепях. Однако на практике использовать такие источники невыгодно по следующим причинам:

Практическим решением проблемы получения случайных чисел стали псевдослучайные числа, то есть такие, которые обладают некоторыми их свойствами, но генерируются по заранее заданному алгоритму. Для их получения используются специальные вычислительные программы — генераторы псевдослучайных чисел. Особенность их работы заключается в том, что через определенный период времени генерируемые последовательности начинают повторяться. В некоторых областях информатики, таких как криптография (шифрование), это имеет критическое значение. Поэтому еще в 50-х годах XX века был предложен способ генерации псевдослучайных чисел на основе строки Фибоначчи (метод Фибоначчи с запаздыванием), который позволил повысить степень случайности в числовых последовательностях. Он успешно используется сегодня не только в криптографии, но и в имитационном моделировании различных естественных, социальных, экономических процессов, например:

Числа Фибоначчи в трейдинге

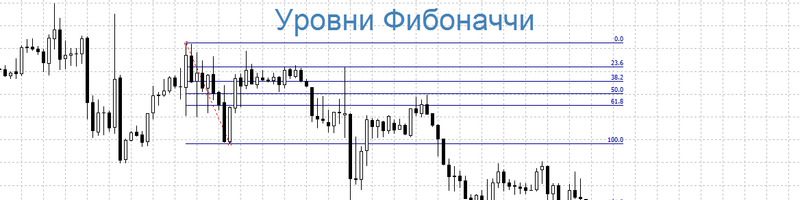
Закономерность, описываемая последовательностью Леонардо Пизанского, получила неожиданное применение в биржевой торговле. В 30-х годах прошлого века американский инженер и менеджер Ральф Нельсон Эллиотт провел масштабное исследование фондов и заметил, что их колебания происходят в определенном ритме, в котором прослеживалось все то же золотое сечение — 0,61803. Сам исследователь делал все вычисления и прогнозы вручную, однако сегодня существуют специальные биржевые программы (терминалы), предлагающие несколько инструментов на основе закономерности Фибоначчи: уровни, дуги, веера и т.д.

Следует отметить, что использование этой закономерности в трейдинге носит спорный характер. Хотя цикличность рынка и фондовых показателей действительно существует, на нее влияет множество факторов, которые невозможно предугадать строгими математическими законами. Тем не менее в ситуации минимального внешнего влияния использование биржевых инструментов, построенных на строках Фибоначчи, действительно позволяет с определенной эффективностью прогнозировать поведение цен, индексов акций.

Числа Фибоначчи в визуальном искусстве и дизайне

Золотая спираль, основанная на последовательности чисел Фибоначчи, является одним из универсальных принципов построения пропорций. Лежащее в ее основе золотое сечение было известно еще в государствах Древнего Востока, но особую популярность оно приобрело в эпоху Возрождения. Великие скульпторы и живописцы того времени начали применять золотую спираль для построения художественной композиции, пропорций различных объектов, в том числе человеческого тела. Золотое сечение сегодня используется как одна из моделей для гармоничного распределения объектов в кадре (в фото- и киноискусстве), элементов плакатов и т.д.

В компьютерную эру золотое сечение (золотая спираль) и числа Фибоначчи также нашли свое применение в визуальном искусстве, в частности, 2D/3D-моделировании и веб-дизайне:

Заблуждения, связанные с числами Фибоначчи

Благодаря современной поп-культуре с этой числовой последовательностью связано множество популярных мифов:

Вместе с тем нельзя отрицать большую роль фибоначчиевых чисел в развитии фундаментальной и прикладной математики, информатики и смежных с ними наук. Разработанные на основе золотой спирали методы и технологии широко применяются в разных областях человеческой жизни, от сугубо научных до прикладных, таких как компьютерная графика, криптография, программирование, обработка данных и т.д.

Источник

Последовательность Фибоначчи: что это такое простыми словами, где применяется и как определяется

Человечество на протяжении многих тысяч лет сталкивалось с различными закономерностями в окружающем их мире. По мере развития науки люди начали описывать многие вещи с помощью математических инструментов. Создание моделей позволяет понять суть различных процессов, а также создает возможность прогнозирования. Один из таких способов – последовательность Фибоначчи.

Как Леонардо Фибоначчи изобрел свою известную последовательность

Леонардо Пизано по прозвищу Фибоначчи – европейский математик 12 в. Родом из Пизы, он по воле отца направился для изучения математики и торгового дела в Алжир к арабским учителям.

Фибоначчи открыл свою известную последовательность, когда задался вопросом о разведении кроликов. Суть задачи: «Пару кроликов заселяют на поляну. Сколько пар будет жить на этом месте через год?». Для решения были введены упрощения: кролики в течение года не умирают, половой зрелости достигают спустя месяц после рождения, потомки появляются только спустя месяц после зачатия.

Таким образом, в этой задаче последовательность определяется так:

В конце года на поляне будет 144+233=377 пар кроликов.

Что это и для чего нужно

Последовательность Фибоначчи простыми словами – это прогрессия, состоящая из целых чисел, следующих друг за другом с определенной закономерностью. Каждый последующий элемент равен сумме двух предыдущих.

Большой интерес представляет частное двух соседних чисел, для всех элементов ряда приблизительно равное цифре 1,618. Это значение получило название «золотое сечение». Именно оно лежит в основе натуральной гармонии нашей Вселенной, присущей галактикам, цветам, животным.

Последовательность чисел Фибоначчи

Так исторически сложилось, что первыми выявили и описали «золотое сечение» древнегреческие математики. Оно представляло собой деление отрезка АВ точкой С на части таким образом, что большая часть отрезка относится к меньшей, как весь отрезок к большей части: ВС/АС=АВ/ВС.

Позднее, в начале 13-го века, Фибоначчи привел обоснование и доказательства существования этой последовательности и «золотого сечения». В 19 веке теоретик Эдуард Люка дал название этой прогрессии — «последовательность Фибоначчи».

Где используют

Золотое сечение наряду с загадочными свойствами чисел Фибоначчи с далеких времен и по сей день привлекают внимание ученых. Область применения последовательности довольна широка. Это может быть искусство, архитектура. Например, правило встречается на полотне И. Левитана «Сумерки. Луна» с выстроенным центром (Луной), линией горизонта, темными акцентами по правилам золотого сечения в соотношении 1,618. Соответственно, здесь и будут расположены наиболее важные части экспозиции.

В архитектуре пример «золотых» линий — знаменитая пирамида Хеопса. В древнегреческих строениях универсальное правило можно проследить, изучая Парфенон. В те времена считалось, что объекты с именно таким соотношением частей наиболее приятны для глаз человека.

Применение в трейдинге

Первым человеком, кто решил заняться изучением рынков на основе применения последовательности чисел Фибоначчи, является Ральф Нельсон Эллиот. Будучи финансистом, он смог обнаружить и определенную закономерность в поведении фондовых рынков, также поддающихся правилу золотого сечения.

Применение последовательности Фибоначчи в трейдинге

Коррекции Фибоначчи

Коррекции, или уровни Фибоначчи – это инструмент технического анализа, служащий для прогнозирования уровней поддержки и сопротивления.

Для построения требуется произвести следующий порядок действий:

Значения коэффициентов получают по следующей формуле, согласно числам Фибоначчи (0,1,1,2,3,5,8,13,21,34,55,89,144…):

Существуют еще 3 уровня, не входящих в соотношения Фибоначчи:

Дуги Фибоначчи

Один из индикаторов, представляющий дуги, которые могут быть уровнями поддержки и сопротивления. Трейдеры при помощи этого инструмента имеют возможность прогнозировать моменты разворота рынка, чтоб своевременно зафиксировать прибыль.

Построение производят также на основе экстремумов графика. Определяют желаемую точку. Затем от нее на расстояниях 38,2%, 50% и 61,8% отстраивают дуги.

Тем самым можно определить уровни сопротивления и поддержки цены.

При растущем тренде с помощью дуг возможно понять, до какого значения опустится цена перед ее следующим подъемом. И, наоборот, при снижении цены акции дуги показывают, как может вырасти цена до ее следующего падения.

Веера Фибоначчи

Представляют диагональные линии, исходящие из одной точки. Формой походят на веер.

Для построения требуется произвести следующие действия;

Временные зоны Фибоначчи

Это инструмент технического анализа рынка, который представляет ряд вертикальных линий, построенных в рамках числовых значений Фибоначчи. Принцип работы основан на временных отрезках, а не на движении цен.

На графике отмечают явный ценовой тренд, основанный на точках экстремума. Горизонтальное расстояние между ними – единичный отрезок. Далее строят параллельные вертикальные линии. Эти прямые будут характеризовать временные зоны, в которых с некоторой долей вероятности можно ожидать падение или взлета цен. Первый уровень должен совпадать с пиковым значением тренда на графике. Но для большей уверенности желательно, чтоб и второй уровень приходился на экстремальное значение.

Источник

Уровни Фибоначчи. Что это и как их использовать в трейдинге

Золотое сечение или с чего все начиналось

Те, кого интересует сугубо прикладной аспект данных инструментов, могут пропустить этот раздел — экскурс в историю чисел Фибоначчи, а также их появления в трейдинге.

Последовательность Фибоначчи была хорошо известна еще в древней Индии, где применялась в стихосложении. Но имя свое она получила благодаря европейскому математику XII века Леонардо Пизанскому, более известному по псевдониму Фибоначчи. Фибоначчи, помимо других многочисленных математических задач, подробно исследовал и описал эту последовательность в труде «Liber Abaci» («Книга Абака» или «Книга об Абаке»). Последовательность эта представляет из себя бесконечный ряд чисел, каждый следующий член которого равен сумме двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

У этого ряда есть много замечательных математических особенностей, но главным является то, что отношение члена ряда к предыдущему стремится к знаменитому «Золотому сечению» — числу 1,618. Это число известно с античных времен и впервые встречается в «Началах» Евклида (около 300 лет до н. э.), где применялось для построения правильного пятиугольника.

Золотое сечение считается наиболее гармоничной пропорцией отношения целого к части. Магическим образом число 1,618 очень часто встречается в природных формах, напрямую не имеющих ничего общего между собой. Эту пропорцию можно заметить в раковинах улиток, расстоянии между листьями на ветке, форме спиралей галактик и даже в среднестатистическом соотношении частей тела человека.

Белорусский ученый Эдуард Сороко, который изучал формы золотых сечений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм — это закручивание по спирали.

В музыкальных произведениях, стихотворениях и художественных произведениях также встречается пропорция 1,618. Ученые умы XIX века признали золотое сечение эталоном гармонии пропорций в природе.

Идея искать золотое сечение в графиках биржевых котировок принадлежала американскому инженеру и управленцу Ральфу Hельсону Эллиотту, который увлекся анализом цен после серьезной болезни в начале 1930х гг. Эллиотт изучал годовые, месячные, недельные, дневные, часовые и получасовые графики различных фондовых индексов, охватывающих 75-летнюю историю поведения рынка. В процессе исследования он заметил, что движения индексов подчинены определенным ритмам — волнам, в пропорциях которых прослеживаются те самые 1,618. Эллиот написал на эту тему ряд трудов, самым масштабным из которых стала книга «Закон природы — секрет вселенной» (англ. Nature’s Law — The Secret of the Universe)», в которую он включил все свои наработки, касающиеся теории волн и соотношения Фибоначчи.

После Эллиота многие трейдеры и исследователи рынка искали различные применения числам Фибоначчи в биржевой торговле. Развитие вычислительной техники позволило аналитикам далеко продвинуться в этом направлении. Современные трейдеры активно используют инструменты, основанные на данном математическом.

Уровни Фибоначчи в биржевой торговле

Пожалуй, самый распространенный терминал для торговли на российском фондовом рынке Quik предлагает пользователю четыре инструмента, основанных на последовательности Фибоначчи. Это уровни, веер, дуги и временные зоны Фибоначчи. Начнем с самых популярных — уровней.

Одним из самых старых и надежных инструментов трейдера являются широко распространенные уровни поддержки и сопротивления. Участникам рынка нужны ценовые ориентиры, чтобы понять, выгодно ли покупать сейчас, не пора ли продавать и где цена может сменить свое направление. Однако не всегда удается точно определить, какой уровень отработает, а какой цена даже не заметит. Как раз эту проблему помогают решить уровни Фибоначчи.

Определение уровней коррекции

По правилам, инструмент «Уровни Фибоначчи» растягивается от начала тренда к его окончанию (на самом деле, если вы растянете уровни наоборот от конца к началу, в Quik разницы не будет). Если растянуть его таким образом, то получившиеся уровни станут возможными целям для коррекции. От этих уровней можно входить по тренду, либо использовать в качестве цели в контр-трендовых сделках.

На примере графика акций «Норильского никеля» хорошо видно, как четко были отработаны уровни 23,6 и 38,2. Причем тут есть особенность: если уровень Фибоначчи совпадает с уровнем на графике, как в данном примере, то вероятность, что он будет отработан, становится очень высокой. Еще лучше, если при этом он будет расположен на круглом числе.

Стоит сразу оговорить ограничение применения. Данный инструмент применяется только при наличии явно выраженного тренда. Если применять его на инструменте, который движется внутри боковика, то уровни отрабатываются очень «грязно», и вряд ли их использование принесет вам прибыль в долгосрочной перспективе.

Движение по Русгидро происходило внутри флэта с большим откатом. В этом случае уровень 23,6 отработал очень «грязно», и цена могла много раз зацепить стоп-заявку.

Также, уровни становятся более «грязными», когда фаза коррекции затягивается. Однако и в этом случае уровни коррекции по Фибоначчи могут оставаться актуальными, причем могут работать в том числе и зеркально.

Еще одним способом применения коррекционных уровней может быть торговля откатов. Когда инструмент делает быстрое движение к значимому уровню, от которого высока вероятность отката, коррекционный уровень 38,2 может показать вам потенциал, до которого можно держать позицию.

Что касается таймфреймов, применять инструмент стоит в диапазоне таймфреймов М15 — D1.

Определение волн Эллиота

Часто уровни Фибоначчи используются в связке с волновой теорией Эллиота. Согласно этой теории, любое трендовое движение по финансовому инструменту можно разложить на пять волн: три основных (импульсных) по тренду и две коррекционных против тренда. Импульсные волны нумеруются как первая, третья и пятая, а коррекционные, в свою очередь, вторая и четвертая.

Любое коррекционное движение тоже можно разложить, но только на три волны. Все внутренние волны также раскладываются по принципу фрактала (фрактал — самоподобная структура). Наглядно этот процесс представлен на рисунке ниже.

Понимание, какую волну формирует цена сейчас, дает возможность предположить, куда она пойдет далее. Самой интересной для трейдеров является третья волна. Она считается самой длинной и самой быстрой. Идеальная сделка с использованием теории Эллиота — это войти в сделку в конце второй волны и выйти из неё в конце третьей.

Согласно теории, высота 3-й волны относится к 1-й, как 1,618. Значит, если мы видим уже сформировавшиеся 1-ю и 2-ю волны, то мы можем рассчитать длину 3-й, используя уровни Фибоначчи. Для этого в некоторых терминалах специально предусмотрен инструмент «расширение Фибоначчи». Строится он по трем точкам: начало первой волны, конец первой волны и конец второй волны. (главное соблюсти эти точке на ценовой шкале по вертикали. По горизонтали положение точек не так важно). На экране появятся уровни Фибоначчи, и уровень с отметкой 1,618 будет отмечать расчетный конец третьей волны.

В терминале Quik инструмента «расширение Фибоначчи» нет. Но его можно заменить обычными уровнями Фибоначчи. Для этого нужно растянуть их так, чтобы 0 был на начале первой волны, а 100 на её окончании. А потом просто перетащить всю конструкцию так, чтобы 0 оказался в конце второй волны.

Хочется отметить, что не всегда конец третьей волны приходится на уровень 1,618. Довольно часто цена немного не доходит или немного опережает эту отметку.

Помимо определения длины третьей волны, ряд специалистов предлагали способы определения и других волн. В книге Б. Вильямса «Торговый хаос» предлагается следующая система определения длин волн:

1 волна — определяется по факту формирования

2 волна — чаще всего заканчивается на уровнях коррекции 50,0 и 61,8.

3 волна — составляет от 1 до 1,618 от длины первой волны.

4 волна — чаще всего заканчивается между уровнями коррекции 38,2 и 50,0 и чаще всего выглядит в виде бокового движения.

5 волна — составляет от 61,8% до 100% от диапазона между началом первой волны и концом третьей.

Рассмотрим на примере графика Россетей. Зеленым отмечены импульсные волны, а красным — коррекционные.

Самым сложным в применении волн Эллиота является вопрос: «В какой волне цена находится сейчас?» Консенсуса по поводу того, как определить точку отсчета первой волны у адептов волновой теории нет по сей день и, возможно, так и не будет.

С практической точки зрения наиболее эффективным является подход: «Не уверен — не торгуй». На некоторых инструментах в определенной фазе волны прорисовываются очень четко и легко идентифицируются. На других же, выделить волны практически невозможно. Необходимо путем регулярного наблюдения отыскивать среди всего многообразия инструментов те, которые ходят понятным для вас образом, и торговать только их. А как только волны начинают ломаться, переходить на другой инструмент.

Очень важно не зацикливаться на одной ценной бумаге, пытаясь отыскать волны там, где их нет. Кроме того, торговая система обязательно должна включать в себя план на случай негативного стечения событий. Стоп—лосс должен обеспечивать соотношение риск/прибыль не менее 1/2.

Веер Фибоначчи

Как и уровни, этот инструмент, может использоваться для определения точек, где завершится коррекция. Алгоритм, по которому строятся лучи веера достаточно простой. Если провести вертикальную линию через точку окончания трендового движения, то лучи будут проходить через точки пересечения этой линии с соответствующими уровнями Фибоначчи. В большинстве терминалов этот алгоритм представлен в виде готового инструмента, который растягивается от начальной точки трендового движения к её концу. Лучи веера, в таком случае, будут показывать возможные окончания коррекции, где можно открывать позицию по тренду.

Веер рекомендуется использовать в связке с другими методами определения длины коррекции. Построение веера имеет погрешность в зависимости от масштаба и таймфрейма, что может привести к неверной трактовке сигналов.

Дуги Фибоначчи

В отличие от предыдущих инструментов, дуги примечательны тем, что они учитывают еще и временной фактор. Это позволяет трейдеру не только предположить, как поведет себя цена, но и в какой момент это произойдет.

Дуги Фибоначчи строятся следующим образом: сначала между началом и концом тренда строится прямая. Затем строятся три дуги с центром в конце пересекающие прямую на уровнях Фибоначчи 38,2%, 50% и 61,8%. В большинстве терминалом дуги, точно так же реализованы в виде отдельного инструмента.

Дуги Фибоначчи очень сильно зависят от масштаба графика. Наиболее подходящий масштаб можно выбрать проанализировав эффективность инструмента на истории. Так же, как и веер рекомендуется использовать дуги совместно с другими методами технического анализа.

Временные зоны Фибоначчи

В основе временных зон Фибоначчи положена одноименная последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21… Исходной точкой для построения выбирается локальный максимум или минимум. Вторая точка позволит определить длину единичного интервала. На графике появятся вертикальные линии с шагом, соответствующем последовательности чисел Фибоначчи в единичном интервале.

Вертикальные линии помогают идентифицировать моменты времени, когда стоит ожидать разворота. При нахождении цены в районе очередной линии необходимо использовать другие индикаторы и сигналы для поиска точки входа против движения. Можно, например, комбинировать временные зоны с веером или уровнями Фибоначчи.

Другие инструменты

Помимо представленных способов использования чисел Фибоначчи в торговле придумана еще масса вариантов: спираль Фибоначчи, канал Фибоначчи, клин Фибоначчи и т. д. Они немного отличаются по методам построения и внешнему виду, но суть их одна — определение длины коррекции. Вы можете выбрать наиболее подходящие для себя инструменты и пополнить ими свой торговый арсенал.

Книги, которые можно прочитать на эту тему

В книге А. Фроста и Р. Пректера «Волновой принцип Эллиота» можно ознакомиться с основными принципами волновой теории Эллиота в её классическом виде.

В книге Б. Мендельброта и Р. Хадсона «(Не)послушные рынки» можно прочесть о современном взгляде на ритмы финансовых рынков и фрактальной структуре изменения цен.

В книге Б. Вильямса «Торговый хаос» можно подробнее ознакомиться с методом подсчета волн, кратко изложенном в данном материале.

В книге Р. Фишеpа «Последовательность Фибоначчи: приложения и стратегии для трейдеров» изложен еще один взгляд на использование уровней Фибоначчи при подсчете волн.

БКС Экспресс

2 обучающих курса

Числа Фибоначчи — что это и для чего они нужны?

Научитесь грамотно оценивать стоимость компании не только с фундаментальной точки зрения, но и «со стороны рынка».

История чисел Фибоначчи

Леонардо Пизано, по прозвищу Фибоначчи, — итальянский математик — родился в Пизе в 1170 году. Его отец работал в торговом порту на северо-востоке Алжира и часто путешествовал.

Фибоначчи изучал математику и во время обширных путешествий познакомился с индийско-арабской системой счисления. Оттуда математик и узнал о числовой последовательности, которую в древней Индии использовали в стихосложении.

Названа последовательность в честь итальянца, потому что именно он представил ее европейскому обществу в труде «Книга абака».

Что такое числа Фибоначчи?

Числа Фибоначчи — это ряд, состоящий из целых чисел. Их особенность заключается в том, что каждый элемент представляет собой сумму двух предыдущих чисел.

Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности.

Математик обратил внимание на числовую последовательность, когда думал о разведении кроликов.

Задача была поставлена следующим образом: «Если новорожденную пару кроликов, самца и самку, поместить в поле, то сколько пар кроликов будет через год?». Но как известно, ни одну практическую задачу невозможно решить без некоторых ограничений и предположений. Поэтому, к условию задачи добавились следующие допущения:

Схема разведения кроликов выглядит следующим образом:

Так как по условию задачи в поле поместили новорожденных кроликов, то спариваться они не могут, так как не достигли половой зрелости. Через месяц кролики начинают спариваться и еще через один – рождается первая пара потомков. «Родители» продолжают наращивать потомство, а дети месяц ждут своего взросления, чтобы тоже стать родителями. В итоге, через 3 месяца по полю будут бегать три пары кроликов. Через 4 месяца уже 5 пар, а через 5 месяцев – 8.

Уже прослеживается закономерность. В конце каждого месяца количество пар кроликов будет больше, чем в предыдущем месяце ровно на столько, сколько пар было два месяца назад.

С точки зрения математики — это красивая последовательность. Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.

Это соотношение можно найти во предметах, которые нас отгружают: гармония в гранях снежинок, в расположении лепестков цветов, ячеек ананаса, завитки раковин у улитки — все подчиняется правилу золотого сечения. Даже строение нашего тела гармонично: если измерить наш рост и разделить на расстояние от пояса до ступней или длину руки на расстояние от локтя до кончиков пальцев, получится известное нам соотношение 1,618.

Если мы видим человека и его внешность кажется красивой, то скорее всего пропорции его лица соотносятся с соотношением чисел Фибоначчи.

Природа полагается на эту врожденную пропорцию для поддержания баланса.

Финансовые рынки имеют ту же математическую основу, что и перечисленные природные явления. Давайте рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.

Числа Фибоначчи в трейдинге

Впервые изучением графиков биржевых котировок и поиском взаимосвязей занялся Ральф Hельсон Эллиотт, американский финансист. Ему удалось обнаружить в поведении фондового рынка особую гармонию. Как вы уже догадались – гармонию золотого сечения.

Мы рассмотрим четыре инструмента технического анализа, использующих последовательность Фибоначчи, активно применяемые трейдерами – это уровни, дуги, веер и временные зоны Фибоначчи.

Сначала поговорим об уровнях коррекции.

1. Коррекции Фибоначчи

Коррекция Фибоначчи — популярный инструмент, используемый трейдерами. Еще больше об инструментах, которые используют трейдеры, можно узнать на открытом курсе «Трейдинг и личные инвестиции».

Как это работает: берутся экстремальные точки на графике акций: нижний и верхний уровни цены долгосрочного тренда, и вертикальное расстояние между ними делится на коэффициенты Фибоначчи: 23,6%, 38,2%, 50%, 61,8% и 100%. После определения уровней соотношений на графике рисуются горизонтальные линии, представляющие уровни, указывающие на возможные уровни поддержки (цена перестает идти ниже) и сопротивления (цена перестает идти выше).

Откуда берутся эти значения процентов?

Трейдеры используют уровни коррекции Фибоначчи для определения стратегических моментов для получения выгодной цены. Если тренд возрастает, то уровни коррекции Фибоначчи используются как потенциальные точки покупки при откатах, если тренд убывающий, то как точки входа для коротких продаж.

2. Дуги Фибоначчи

Дуги Фибоначчи учитывают как время, так и цену, также указывая на потенциальные области поддержки и сопротивления.

Поиск максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем рисуются три изогнутые линии, похожие на полукруги, на расстоянии 38,2%, 50% и 61,8% от желаемой точки. Полукруглые дуги показывают, где цена находит поддержку или сопротивление в будущем.

После роста цены дуги показывают до чего цена может откатиться, прежде чем снова начнет расти. После снижения цены дуги показывают, куда цена может подняться, прежде чем снова начнет падать.

3. Веера Фибоначчи

Веера Фибоначчи — это диагональные линии, образующие веер. Как и в предыдущих методах, сначала находятся максимум и минимум тренда. Если траектория возрастающая, то через точку максимума, если убывающие – через точку минимума условно проводится вертикальная линия.

Затем на линии отмечаются уровни: 38,2%, 50% и 61,8%. Дальше соединяются точки первого экстремума и точки, условно отмеченные на невидимой прямой. Получившиеся диагональные линии также указывают на области поддержки и сопротивления.

4. Временные зоны Фибоначчи

Временные зоны — это серия линий, параллельных оси ОУ, отстоящих друг от друга на расстоянии, пропорциональном элементам последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. д.).

Трейдер отмечает на графике очевидный ценовой тренд (его минимум и максимум). Расстояние между этими точками будет задавать единичный отрезок. Дальше рисуются прямые линии соответственно последовательности Фибоначчи: представьте, что вы строите график на координатной плоскости OXY. Ось OX разбита на длины единичного отрезка от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8…. и так далее.

Теперь вспомним, как выглядит ряд Фибоначчи: 0, 1, 2, 3, 5, 8…. Теперь именно в этих точках на оси OX и будут строиться вертикальные линии, соответствующие временным зонам. Каждая линия указывает время, в которое можно ожидать резкий скачок или спад цены.

Описанные инструменты далеко не единственные методы анализа графиков, использующих золоте сечение и числа Фибоначчи. Возможно, вы слышали и о таких инструментах, как клин, канал, спираль, также названных в честь Фибоначчи. Они отличаются способами построения и внешним видом, но смысл остается один — оценить области поддержки и сопротивления цены. Часто используют несколько методов одновременно для улучшения качества прогнозирования. Подробнее об инструментах, которые используются в трейдинге, можно узнать в бесплатной демо-версии книги по трейдингу.

Надеемся, вы тоже найдете собственное «нишевое» применение исследованиям Фибоначчи и добавите эти методы в свой набор инвестиционных инструментов.

Автор: Алексанян Андрон, эксперт SF Education

Источник

Золотое сечение и числа Фибоначчи

Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.

Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].

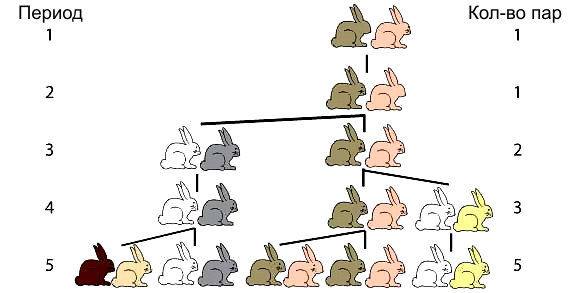
Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).

Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].

В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).

Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].

Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].

Золотые пропорции включают в себя такие моменты:

— как ширина верхнего переднего зуба относится к ширине нижнего;

— как соотносятся между собой по ширине:

2 резца в нижнем фронтальном ряду;

двое резцов в верхнем ряду;

— какое имеется расстояние между премолярами и т.д.

Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».

Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].

Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:

• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;

• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;

• 2 — понимает речь и действует, пользуясь словесными указаниями;

• 3 — действует посредством слова, задаёт вопросы;

• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;

• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…

Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.

1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.

Источник

Магия чисел: что такое последовательность Фибоначчи

Александра Смаракова

Последовательность Фибоначчи — это ряд чисел, в котором первые два элемента — 0 и 1, а все последующие равны сумме двух предыдущих. Ее можно проследить в некоторых явлениях природы, науке, архитектуре и искусстве. Разбираемся в том, что это такое и почему важно.

Леонардо Пизанский: математика и удача

Леонардо Пизанский (ок. 1170 — ок. 1250) был математиком. Он жил в Италии, а в 1190-х годах переехал в Алжир, где узнал об арабских и индийских приемах вычисления. В 1200 году Леонардо вернулся в Пизу, а в 1202 дописал свой первый труд по математике — «Книгу абака» (абаком он называл арифметику). Именно в этой работе была описана последовательность чисел, которую впоследствии назвали последовательностью Фибоначчи.

Фибоначчи — это прозвище Леонардо Пизанского, которое появилось только в XVI веке. Оно происходит от слов filius Bonacci, которые стояли на обложке «Книги абака». Их можно перевести как «сын Боначчо» (или «Боначчи», если трактовать это слово как фамилию, а не как имя). По другой версии, Bonacci нужно тоже понимать как прозвище — в итальянском это слово означает «удача».

Последовательность Фибоначчи впервые была рассмотрена на примере вымышленной популяции кроликов. Математик сформулировал задачу: в загоне есть пара кроликов, которая каждый месяц производит на свет новую пару. Сколько всего кроликов будет через год? При этом надо учесть несколько условий:

Кролики могут принести потомство только на третий месяц жизни.

Кролики всегда рождаются парами — самка и самец.

Кролики не умирают в течение года.

При решении этой задачи возник ряд чисел, который выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 — в конце года будет 233 пары кроликов.

Это и есть последовательность Фибоначчи, которую можно продолжать бесконечно.

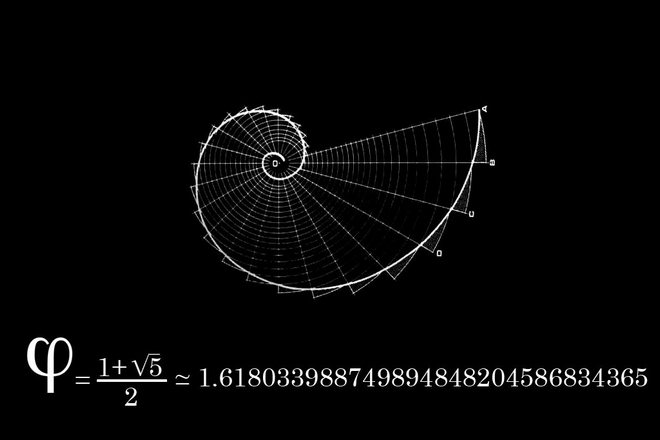
Золотое сечение и спираль Фибоначчи

Если последовательно делить одно число ряда Фибоначчи на предыдущее, в конце концов (с деления 89 на 55) мы начнем получать число 1,618. Именно этот коэффициент принято называть золотым сечением, или золотой пропорцией. А если мы попробуем изобразить это графически, то получим золотой прямоугольник — длины его сторон будут относиться друг к другу как 1,618 : 1.

С помощью золотого прямоугольника можно построить спираль Фибоначчи.

И золотая пропорция, и спираль Фибоначчи интересны тем, что они часто встречаются в природе. Например, семена в центре подсолнечника организованы в спираль и идут по и против часовой стрелки. Если анализировать каждую спираль отдельно, окажется, что это и есть спирали Фибоначчи. То же самое касается раковин некоторых улиток и даже строения человеческого уха. А если посчитать, как соотносится расстояние от точки пупа до коленей и от коленей до ступней в нашем теле, мы получим золотую пропорцию — 1 : 1,618.

Числа Фибоначчи в искусстве

Золотое сечение и спираль Фибоначчи часто используются в живописи или архитектуре. Пожалуй, самый известный пример — это работы Леонардо да Винчи. Композиция «Моны Лизы» построена на основе спирали Фибоначчи, а «Витрувианский человек» буквально изображает связь пропорций тела и золотого сечения.

С использованием золотой пропорции построены, например, египетские пирамиды Гизы, Собор Парижской Богоматери и Храм Василия Блаженного. А в 2005 году в Корнуолле (Великобритания) появился образовательный комплекс The Core («Ядро»). Его архитекторы вдохновлялись формой цветка подсолнечника. В итоге получилось здание, построенное по принципу спирали Фибоначчи.

Считается, что золотое сечение используется также в музыке и поэзии. В некоторых произведениях, например поэме Лермонтова «Бородино» или этюдах Шопена, кульминационные моменты разделяют композицию на части, соотношение которых близко к золотой пропорции.

Источник

Фибоначчи что это такое простыми словами

_{ВЫСШЕЕ НАЗНАЧЕНИЕ МАТЕМАТИКИ СОСТОИТ В ТОМ, ЧТОБЫ НАХОДИТЬ СКРЫТЫЙ ПОРЯДОК В ХАОСЕ, КОТОРЫЙ НАС ОКРУЖАЕТ.}

Человек всю жизнь стремится к знаниям, пытается изучить окружающий его мир. И в процессе наблюдений у него возникают вопросы, на которые требуется найти ответы. Ответы находятся, но появляются новые вопросы. В археологических находках, в следах цивилизации, отдаленных друг от друга во времени и в пространстве, встречается один и тот же элемент – узор в виде спирали. Некоторые считают его символом солнца и связывают с легендарной Атлантидой, но истинное его значение неизвестно. Что общего между формами галактики и атмосферного циклона, расположением листьев на стебле и семян в подсолнухе? Эти закономерности сводятся к так называемой «золотой» спирали, удивительной последовательности Фибоначчи, открытой великим итальянским математиком XIII века.

История возникновения чисел Фибоначчи

Впервые о том, что такое числа Фибоначчи, я услышал от учителя математики. Но, кроме того, каким образом складывается последовательность этих чисел, я не знал. Вот чем на самом деле знаменита эта последовательность, каким образом она влияет на человека, я и хочу вам рассказать. О Леонардо Фибоначчи известно немного. Нет даже точной даты его рождения. Известно, что он родился в 1170 году в семье купца, в городе Пизе в Италии. Отец Фибоначчи часто бывал в Алжире по торговым делам, и Леонардо изучал там математику у арабских учителей. Впоследствии он написал несколько математических трудов, наиболее известным из которых является «Книга об абаке», которая содержит почти все арифметические и алгебраические сведения того времени. 2

Числа Фибоначчи – это последовательность чисел, обладающая рядом свойств. Эту числовую последовательность Фибоначчи открыл случайно, когда пытался в 1202 году решить практическую задачу о кроликах. «Некто поместил пару кроликов в некоем месте, огороженном со всех сторон со всех сторон стеной, чтобы узнать, сколько пар кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения». При решении задачи он учел, что каждая пара кроликов порождает на протяжении жизни еще две пары, а затем погибает. Так появилась последовательность чисел: 1, 1, 2, 3, 5, 8, 13, 21, … В этой последовательности каждое следующее число равно сумме двух предыдущих. Её назвали последовательностью Фибоначчи. Математические свойства последовательности

Мне захотелось исследовать эту последовательность, и я выявил некоторые её свойства. Эта закономерность имеет большое значение. Последовательность все медленнее приближается к некоему постоянному отношению, равному примерно 1, 618, а отношение любого числа к последующему примерно равно 0, 618.

размером 8х8 (всего 64 маленьких квадратика) на четыре части, длины сторон которых равны числам Фибоначчи. Теперь из этих частей построим прямоугольник размером 5х13. Его площадь составляют 65 маленьких квадратиков. Откуда же берется дополнительный квадрат? Все дело в том, что идеальный прямоугольник не образуется, а остаются крошечные зазоры, которые в сумме и дают эту дополнительную единицу площади. Треугольник Паскаля также имеет связь с последовательностью Фибоначчи. Надо только написать строки треугольника Паскаля одну под другой, а затем складывать элементы по диагонали. Получится последовательность Фибоначчи.

Теперь рассмотрим «золотой» прямоугольник, одна сторона которого в 1,618 раз длиннее другой. На первый взгляд он может показаться нам обычным прямоугольником. Тем не менее, давайте проделаем простой эксперимент с двумя обыкновенными банковскими картами. Положим одну из них горизонтально, а другую вертикально так, чтобы их нижние стороны находились на одной линии. Если в горизонтальной карте провести диагональную линию и продлить ее, то увидим, что она пройдет в точности через правый верхний угол вертикальной карты – приятная неожиданность. Может быть, это случайность, а может, такие прямоугольники и другие геометрические формы, использующие «золотое сечение», особенно приятны глазу. Думал ли Леонардо да Винчи о золотом сечении, работая над своим шедевром? Это кажется маловероятным. Однако можно утверждать, что он придавал большое значение связи между эстетикой и математикой.

Числа Фибоначчи в природе

Связь золотого сечения с красотой – вопрос не только человеческого восприятия. Похоже, сама природа выделила Ф особую роль. Если в «золотой» прямоугольник последовательно вписать квадраты, затем в каждом квадрате провести дугу, то получится элегантная кривая, которая называется логарифмической спиралью. Она вовсе не является математическим курьезом. 5

Природа даёт нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидных расположениях мелких частей растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом – против. Числа спиралей одного и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие слева снизу вправо вверх. На многих шишках семена расположены в трёх спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удаётся наблюдать 5 и 8, и даже 8 и 13 спиралей. Хорошо заметны спирали Фибоначчи и на ананасе: обычно их бывает 8 и 13.

Отросток цикория делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс. Импульсы его роста постепенно уменьшаются в пропорции «золотого» сечения. Чтобы оценить огромную роль чисел Фибоначчи, достаточно лишь взглянуть на красоту окружающей нас природы. Числа Фибоначчи можно найти в количестве

ответвлений на стебле каждого растущего растения и в числе лепестков.

Пересчитаем лепестки некоторых цветов —ириса с его 3 лепестками, примулы с 5 лепестками, амброзии с 13 лепестками, нивяника с 34 лепестками, астры с 55 лепестками и т.д. Случайно ли это, или это закон природы? Посмотрите на стебли и цветы тысячелистника. Таким образом, суммарной последовательностью Фибоначчи можно легко трактовать закономерность проявлений «Золотых» чисел, встречаемых в природе. Эти законы действуют независимо от нашего сознания и желания принимать их или нет. Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов, в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Числа Фибоначчи в архитектуре

«Золотое сечение» проявляется и во многих замечательных архитектурных творениях на протяжении всей истории человечества. Оказывается, еще древнегреческие и древнеегипетские математики знали эти коэффициенты задолго до Фибоначчи и называли их «золотым сечением». Принцип «золотого сечения» греки использовали при строительстве Парфенона, египтяне – Великой пирамиды в Гизе. Достижения в области строительной техники и разработки новых материалов открыли новые возможности для архитекторов ХХ века. Американец Фрэнк Ллойд Райт был одним из главных сторонников органической архитектуры. Незадолго до смерти он спроектировал музей Соломона Гуггенхайма в Нью-Йорке, представляющий собой опрокинутую спираль, а интерьер музея напоминает раковину наутилуса. Польско-израильский архитектор Цви Хекер также использовал спиральные конструкции в проекте школы имени Хайнца Галински в Берлине, построенной в 1995 году. Хекер начал с идеи подсолнечника с центральным кругом, откуда

расходятся все архитектурные элементы. Здание представляет собой сочетание

ортогональных и концентрических спиралей, символизируя взаимодействие ограниченных человеческих знаний и управляемого хаоса природы. Его архитектура имитирует растение, которое следует за движением Солнца, поэтому классные комнаты освещены в течение всего дня.

В Куинси-парке, расположенном в Кембридже, штат Массачусетс (США), «золотую» спираль можно встретить часто. Парк был спроектирован в 1997 году художником Дэвидом Филлипсом и находится недалеко от Математического института Клэя. Это заведение является известным центром математических исследований. В Куинси-парке можно прогуливаться среди «золотых» спиралей и металлических кривых, рельефов из двух раковин и скалы с символом квадратного корня. На табличке написана информация о «золотой» пропорции. Даже парковка для велосипедов использует символ Ф.

Числа Фибоначчи в психологии

В психологии отмечены переломные моменты, кризисы, перевороты, знаменующие на жизненном пути человека преобразования структуры и функций души. Если человек успешно преодолел эти кризисы, то становится способным решать задачи нового класса, о которых раньше даже не задумывался.

Наличие коренных изменений дает основание рассматривать время жизни в качестве решающего фактора развития духовных качеств. Ведь природа отмеряет нам время не щедро, «ни сколько будет, столько и будет», а ровно столько, чтобы процесс развития материализовался:

в структурах тела;

в чувствах, мышлении и психомоторике — пока они не приобретут гармонию, необходимую для возникновения и запуска механизма

в структуре энергопотенциала человека.

Развитие тела нельзя остановить: ребенок становится взрослым человеком. С механизмом же творчества не так все просто. Его развитие можно остановить и изменить его направление.

Существует ли шанс догнать время? Безусловно. Но для этого нужно выполнить огромную работу над собой. То, что развивается свободно, естественным путем, не требует специальных усилий: ребенок свободно развивается и не замечает этой огромной работы, потому что процесс свободного развития создается без насилия над собой.

Как понимается смысл жизненного пути в обыденном сознании? Обыватель видит его так: у подножия — рождение, на вершине — расцвет сил, а потом — все идет под горку.

Мудрец же скажет: все намного сложнее. Восхождение он разделяет на этапы: детство, отрочество, юность… Почему так? Мало, кто способен ответить, хотя каждый уверен, что это замкнутые, целостные этапы жизни.

Чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека.

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет: 0 — начало отсчета — ребенок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;

1 — ребенок овладел ходьбой и осваивает ближайшее окружение;

2 — понимает речь и действует, пользуясь словесными указаниями;

3 — действует посредством слова, задает вопросы;

5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребенку охватить мир во всей его целостности;

8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии жизни;

13 — начинает работать механизм таланта, направленный на превращение приобретенного в процессе наследования материала, развивая свой собственный талант;

21 — механизм творчества приблизился к состоянию гармонии и делаются попытки выполнять талантливую работу;

34— гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;

55 — в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее…

Что же такое засечки «Чисел Фибоначчи»? Они могут быть сравнимы с плотинами на жизненном пути. Эти плотины ожидают каждого из нас. Прежде всего необходимо преодолеть каждую их них, а потом терпеливо поднимать свой уровень развития, пока в один прекрасный день она не развалится, открывая свободному течению путь к следующей.

Теперь, когда нам понятен смысл этих узловых точек возрастного развития, попробуем расшифровать, как все это происходит.

В1 год ребенок овладевает ходьбой. До этого он познавал мир передней частью головы. Теперь же он познает мир руками — исключительная привилегия человека. Животное передвигается в пространстве, а он, познавая, овладевает пространством и осваивает территорию, на которой живет.

2 года — понимает слово и действует в соответствии с ним. Это значит, что:

ребенок усваивает минимальное количество слов — смыслов и образов действий;

пока что не отделяет себя от окружающей среды и слит в целостность с окружающим,

поэтому действует по чужому указанию. В этом возрасте он самый послушный и приятный для родителей. Из человека чувственного ребенок превращается в человека познающего.

3 года— действие при помощи собственного слова. Уже произошло отделение этого человека от окружающей среды — и он учится быть самостоятельно действующей личностью. Отсюда он:

сознательно противостоит среде и родителям, воспитателям в детском саду и т.д.;

осознает свой суверенитет и борется за самостоятельность;

старается подчинить своей воле близких и хорошо знакомых людей.

Теперь для ребенка слово — это действие. С этого начинается действующий человек.

5 лет— «возраст грации». Он — олицетворение гармонии. Игры, танцы, ловкие движения — все насыщено гармонией, которой человек старается овладеть собственными силами. Гармоничная психомоторика содействует приведению к новому состоянию. Поэтому ребенок направлен на психомоторную активность и стремится к максимально активным действиям.

Материализация продуктов работы чувствительности осуществляется посредством:

способности к отображению окружающей среды и себя как части этого мира (мы слышим, видим, прикасаемся, нюхаем и т.д. — все органы чувств работают на этот процесс);

способности к проектированию внешнего мира, в том числе и себя

(создание второй природы, гипотез — сделать завтра то и другое, построить новую машину, решить проблему), силами критичности мышления, чувств и воображения;

способности к созиданию второй, рукотворной природы, продуктов деятельности (реализация задуманного, конкретные умственные или психомоторные действия с конкретными предметами и процессами).

После 5 лет механизм воображения выходит вперед и начинает доминировать над остальными. Ребенок выполняет гигантскую работу, создавая фантастические образы, и живет в мире сказок и мифов. Гипертрофированность воображения ребенка вызывает у взрослых удивление, потому что воображение никак не соответствует действительности.

8 лет — на передний план выходят чувства и возникают собственные мерки чувств (познавательных, нравственных, эстетических), когда ребенок безошибочно:

оценивает известное и неизвестное;

отличает моральное от аморального, нравственное от безнравственного;

прекрасное от того, что угрожает жизни, гармонию от хаоса.

13 лет — начинает работать механизм творчества. Но это не значит, что он работает на полную мощность. На первый план выходит один из элементов механизма, а все остальные содействуют его работе. Если и в этом возрастном периоде развития сохраняется гармония, которая почти все время перестраивает свою структуру, то отрок безболезненно доберется до следующей плотины, незаметно для себя преодолеет ее и будет жить в возрасте революционера. В возрасте революционера отрок должен сделать новый шаг вперед: отделиться от ближайшего социума и жить в нем гармоничной жизнью и деятельностью. Не каждый может решить эту задачу, возникающую перед каждым из нас.

21 год. Если революционер успешно преодолел первую гармоничную вершину жизни, то его механизм таланта способен выполнять талантливую

работу. Чувства (познавательные, моральные или эстетические) иногда затмевают мышление, но в общем все элементы работают слаженно: чувства открыты миру, а логическое мышление способно с этой вершины называть и находить меры вещей.

Механизм творчества, развиваясь нормально, достигает состояния, позволяющего получать определенные плоды. Он начинает работать. В этом возрасте вперед выходит механизм чувств. По мере того, как воображение и его продукты оцениваются чувствами и мышлением, между ними возникает антагонизм. Побеждают чувства. Эта способность постепенно набирает мощность, и отрок начинает ею пользоваться.

34 года— уравновешенность и гармоничность, продуктивная действенность таланта. Гармония мышления, чувств и воображения, психомоторики, которая пополняется оптимальным энергопотенциалом, и механизм в целом — рождается возможность исполнять гениальную работу.

55 лет — человек может стать творцом. Третья гармоничная вершина жизни: мышление подчиняет себе силу чувств.

Числа Фибоначчи называют этапы развития человека. Пройдет ли человек этот путь без остановок, зависит от родителей и учителей, образовательной системы, а дальше — от него самого и от того, как человек будет познавать и преодолевать самого себя.

На жизненном пути человек открывает 7 предметов отношений:

От дня рождения до 2-х лет — открытие физического и предметного мира ближайшего окружения.

От 2-х до 3-х лет — открытие себя: «Я — Сам».

От 3-х до 5-ти лет — речь, действенный мир слов, гармонии и системы «Я — Ты».

От 5-ти до 8-ми лет — открытие мира чужих мыслей, чувств и образов — системы «Я — Мы».

От 8 до 13 лет — открытие мира задач и проблем, решенных гениями и талантами человечества — системы «Я — Духовность».

От 13 до 21 года — открытие способностей самостоятельно решать всем известные задачи, когда мысли, чувства и воображение начинают активно работать, возникает система «Я — Ноосфера».

От 21 до 34 лет — открытие способности создавать новый мир или его фрагменты — осознание самоконцепции «Я — Творец».

Жизненный путь имеет пространственно-временную структуру. Он состоит из возрастных и индивидуальных фаз, определяемых по многим параметрам жизни. Человек овладевает в определенной мере обстоятельствами своей жизни, становится творцом своей истории и творцом истории общества. Подлинно творческое отношение к жизни, однако, появляется далеко не сразу и даже не у всякого человека. Между фазами жизненного пути существуют генетические связи, и это обусловливает закономерный его характер. Отсюда следует, что в принципе можно предсказывать будущее развитие на основе знания о ранних его фазах.

Числа Фибоначчи в астрономии

Из истории астрономии известно, что И.Тициус, немецкий астроном XVIII в., с помощью ряда Фибоначчи нашёл закономерность и порядок в расстояниях между планетами солнечной системы. Но один случай, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Но после смерти Тициуса в начале XIX в. сосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов.

Заключение

В процессе исследования я выяснил, что числа Фибоначчи нашли широкое применение в техническом анализе цен на бирже. Один из простейших способов применения чисел Фибоначчи на практике – определение отрезков времени, через которое произойдёт то или иное событие, например, изменение цены. Аналитик отсчитывает определённое количество фибоначчиевских дней или недель (13,21,34,55 и т.д.) от предыдущего сходного события и делает прогноз. Но в этом мне ещё слишком сложно разобраться. Хотя Фибоначчи и был величайшим математиком средних веков, единственные памятники Фибоначчи – это статуя напротив Пизанской башни и две улицы, которые носят его имя: одна – в Пизе, а другая – во Флоренции. И всё-таки, в связи со всем увиденным и прочитанным мною возникают вполне закономерные вопросы. Откуда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Что же будет дальше? Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появятся ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, тринадцатью и т.д. Не забывайте, что на двух руках по пять пальцев, два из которых состоят из двух фаланг, а восемь – из трёх.

Литература:

Волошинов А.В. «Математика и искусство», М., Просвещение, 1992г.

Воробьёв Н.Н. «Числа Фибоначчи», М., Наука, 1984г.

Стахов А.П. «Код да Винчи и ряд Фибоначчи», Питер формат, 2006 г.

Ф. Корвалан «Золотое сечение. Математический язык красоты», М., Де Агостини, 2014 г.

Максименко С.Д. «Сенситивные периоды жизни и их коды».

Источник

Фибоначчи

Леонардо Пизанский, он же Фибоначчи и его уникальная, в своём роде, последовательность чисел, так же как и понятия «золотого сечения», «спираль Фибоначчи» или «число Бога», имеет непосредственное отношение к трейдингу, как к живой среде. На основе последовательности чисел трейдеры выстраивают уровни коррекции, расширения и иные.

Фибоначчи – кто это?

Леонардо Пизанский, больше известен по прозвищу Фибоначчи. Один из первых крупных математиков в средневековой Европе. Изучал искусство счёта в Алжире, Индии, Византии, Египте и ещё во многих странах Евразии и Африки. Его посмертный статус провозглашается как: «Пропагандист десятичной системы счисления и использования арабских цифр». Но в первую очередь, в нашем времени Фибоначчи запомнился нам как искусный математик. Сам он родился в Италии, в Пизанской республике и прожил 80 лет. Умер на родине, не оставив о своей биографии абсолютно ничего (все даты лишь предположения историков), за исключением отрывка второго абзаца книги «Абака». Даже портрет, знаменитого средневекового математика. Это лишь примерные наброски со слов историков.

Последовательность чисел Фибоначчи

Дак какое же отношение Фибоначчи имеет применимо к трейдингу? Наберитесь терпения, дальше самое важное и интересное. Существует выражение, что математика «Царица всех наук». В ней присутствуют темы, с методами вычисления которых, можно раскрыть завесу тайн мировоздания. В мире есть закономерности и явления, которые, как не странно, можно объяснить на языке математики.

Главным важнейшим трудом Фибоначчи, дошедших до наших дней, является последовательность чисел, при котором сумма следующего числа, получается путём сложением двух предыдущих чисел. В письменном виде это выглядит так:

0,1,1,2,3,5,8,13,21,34,55,89,144,…

0+1=1+1=2+1=3+2=5+3=8+5=13+8=21+13=34+21=55+34=89+55=144…

Данная последовательность хорошо прослеживается в задачке от «Фибоначчи»: Есть два кролика, самец и самка. Условия таковы, что каждый месяц у них появляется на свет потомство, тоже самка и самец. На следующий месяц у этой пары появляется ещё одна пара кроликов. Теперь у нас получилось три пары кроликов. На следующий месяц, путём спаривания между собой в парах, у нас уже 5 пар кроликов. Задача состоит в том, чтобы вычислить, сколько будет кроликов, спустя 1 год. Ответ не так уж и сложен, даже без применения каких либо формул. Достаточно прибегнуть к числовой последовательности Фибоначчи, где одна единица любой цифры будет один кролик. А каждое сложение. Это будет прошествие одного месяца. На выходе мы получим 377 кроликов, если начать счисление от 1+1 (кролик + кролик).

«Золотое сечение» (1,618)

Золотое сечение это пропорциональное соотношение чисел, при использовании которого в любой сфере жизнедеятельности, проявляется структуризация и гармония. Но всё же, давайте не будем употреблять заучных слов и рассмотрим это явление простым языком. Для простоты восприятия, возьмём любое число из последовательности чисел Фибоначчи. Например, 13. Чтобы нам обнаружить число «золотого сечения», нам необходимо это число разделить на предыдущее в этом же ряду, то есть на 8. В ответе мы получим десятичную дробь 1,625. То есть это не цельное, не круглое число близкое к «золотому сечению».

Но если мы разделим 144 на 89, то мы получим цифру 1,6179775. Заметили разницу? Во втором примере итоговая цифра изменилась в меньшую сторону. Забегая вперёд, скажу, что чем выше мы будем брать число из последовательности чисел Фибоначчи, тем скорее и ближе будет стремиться итоговая цифра к значению 1,618 (не исключено отклонение как в плюс, так и в минус). К примеру, возьмём далёкое число 10 946 и разделим из этого ряда на предыдущее число 6 765. По итогу получим почти идеальную десятичную дробь 1,6180339. Попрошу вас взять в руки калькулятор и проверить данный пример.

Золотое сечение и трейдинг.

Но какое же отношение, десятичная дробь 1,618 имеет к трейдингу? Потерпите немного, ведь не знание источников информации приводит к неверным интерпретациям будущих ситуаций на рынке. Понимаете, финансовый рынок, это живая среда. Это мы с вами. Для ясного, ну или примерного представления, приведу пример: Как известно из научных источников, насекомые, в частности пчёлы или муравьи, имеют один, общий инстинктивный «разум». И при строительстве своего муравейника, они не общаются, не обсуждают размер будущего дома, и не собираются вместе на обед. Но почему тогда у них получаются их логова в идеальном для них состоянии и в правильно расположенном месте? Да к тому же с меньшими входами/выходами со стороны севера? Всё потому же, что это инстинкт от природы ОДИН на всех. Ровно поэтому же и всемирный коллектив на FOREX, действует «сообща», «инстинктивным» разумом. Совершая всё те же ошибки, отдавая прибыль и преимущество единицам.

Простейший пример

Теперь, зная точное (округлённое) число «золотого сечения». Мы с вами можем рассчитать практически любое соотношение. Снова забегая вперёд, оговорюсь; современный человеческий мозг, до сих пор не хочет воспринимать «идеальные» пропорции, как в природе, так и в архитектуре.

Так в простейший пример можно привести «золотой прямоугольник». То есть прямоугольник с идеальным соотношением сторон. Ширина 754. Высота 466. При делении ширины на высоту, получим десятичную дробь «золотого сечения» 1,6180257. Я по праву не знаю (но догадываюсь) почему данное соотношение сторон не используется на экранах, при выпуске телевизоров или других гаджетов. Но всё же, некоторые устройства имеют приблизительную пропорцию сторон. Я же ссылаюсь на то, что современный человек ещё не пришёл к полной гармонии с «внутренней» природой.

Спираль Фибоначчи

Весь наш мир в изобилие элементами «золотого сечения». Просто люди, которые далеки от этой темы, не в состоянии этого узреть. Сплошь и рядом прослеживается пропорция 1,618. Одним из важнейших элементов «золотого сечения» является спираль Фибоначчи. И вот те, кто разобрался с этой темой, и прочувствовали всю красоту и гармонию данного явления, несомненно, захотят построить спираль Фибоначчи собственными руками. Для этого нам потребуется циркуль обыкновенный и лист в клеточку. Обязательно в клеточку для того, чтобы можно было чертить аккуратные, правильные квадраты. Начать построение спирали нужно с двух нарисованных одинаковых квадратов, размером в одну клеточку, каждый. Начало спирали соединяет два противоположных угла этих квадратиков, лежащих на одной плоскости. Теперь важное условие; следующий квадрат, который соединяет два предыдущих, должен иметь стороны содержащие количество клеточек в сумме полученные путём сложения количеством клеток двух предыдущих квадратов. И каждый раз спираль (дуга) чертится на противоположный угол по диагонали. Да ребят, просто читая, я бы и сам запутался, для этого я и привёл ниже скриншот.

Спираль и ряд чисел Фибоначчи в природе

Последовательность ряда чисел Фибоначчи, «золотое сечение» и Спираль Фибоначчи в архитектуре

Человек, как разумный Хомо сапиенс, тоже стремится к красоте, удобству, гармонии и оптимизации своих творений. Не правильным будет не признать гениальность архитекторов, воздвигнутых под их проектами сооружений. Которые можно описать с помощью математики. В частности все их элементы демонстрируют ряд чисел Фибоначчи, «золотое сечение», либо Спираль Фибоначчи.

Вообще в мире и в истории примеров наглядных уйма. Я же приведу в пример самый простенький. Христианский крест. Предположим мы взяли вертикальный элемент креста длинною, ну скажем 1000 см. Значит, горизонтальная перекладина должна быть 618 см. 1000/1,618=618. Далее располагаем её на уровне тоже 618 см. («золотое сечение» по длине стоявой балки), от верхнего края. Условие, что центр крепежа будет на обеих балках на расстоянии 618 см. В итоге мы получаем крест идеальной формы. И вот что удивительно, если вы из выше предложенного примера, правильно наложите спираль Фибоначчи на этот крест, то некоторые элементы совпадут. Вы сможете это воссоздать сами на листе бумаги в клетку.

Подводя итоги

На эту тему, примеров можно приводить бесчисленное количество. Но из пройденного материала, думаю, многие читатели поняли, почему ряд чисел Фибоначчи называют «числом Бога». Я же, подводя черту, желаю объяснить начинающим трейдерам, специализирующихся на техническом анализе, зачем так важно знать про последовательность чисел Фибоначчи. Рынок, будь то Forex или любая Биржевая площадка, это всегда живая среда. Инфраструктура похожая на природные явления. Это мы с вами. Коллективные действия, формирующие правила и элементы, так похожие на природные закономерности. К сожалению, в рамках этого материала, мне больше нечем вас удивить. Могу лишь посоветовать поинтересоваться этой темой на каналах в YouTube. Ролики с данным сюжетом, по истине, захватывает дух.

Эта статья – материал из рубрики “Азбука Трейдинга”. Загляните в неё. Там ещё много интересного!

Сложно? “Трейдинг для чайников” – бесплатное обучение рынкам.

Подпишитесь на наш телеграм канал и получите самую лучшую информацию.

Источник

Фибоначчи повсюду!

Числа Фибоначчи названы в честь Леонардо Фибоначчи из города Пизы (современная Италия). На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.

Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.

Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Почему эта последовательность настолько уникальна

Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.

Числа Фибоначчи в природе

Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека

Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.

Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.

Числа Фибоначчи в биржевой торговле

Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.

Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.

Числа Фибоначчи в фотографии и искусстве

В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.

Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

Тем не менее, никогда не стоит недооценивать скрытые силы последовательности Фибоначчи.

Источник

Божественная гармония: что такое золотое сечение простыми словами. Тайны мироздания в числах

Эта гармония поражает своими масштабами.

Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?

Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)

Что такое золотое сечение?

Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.

Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».

До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.

Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Источник

Тайна «числа бога»

Число бога? Может быть, вам интересно, что такое «Число Бога»? На самом деле это просто термин для обозначения «загадочного числа». Которое часто встречается в явлениях в природе. Эта цифра на самом деле изучалась многими исследователями, они обычно называют это число «золотым сечением» или «золотым числом».

Что ж, может быть, некоторые из вас знакомы с двумя последними терминами. Да, те из вас, кто читал об этом, наверняка знают, что это число имеет непосредственное отношение к последовательности Фибоначчи.

Вы знаете, почему исследователи называют это золотым числом? Потому что с этими числами связано так много событий в природе. Фактически, до того, как Обама был избран президентом, некоторые предсказывали, что Обама станет 44-м президентом Америки на основе анализа последовательности Фибоначчи.

Последовательность Фибоначчи

Те из вас, кто закончил среднюю школу, наверняка слышали число Фибоначчи в математике. Что такое числа Фибоначчи? Числа Фибоначчи – это последовательность чисел, составленная Леоанардо Фибоначчи в 1175–1245 годах. Числа Фибоначчи также известны как золотое число человеческой жизни.

Хотите верьте, хотите нет, но, по мнению ученых древних времен, число Фибоначчи является одним из доказательств существования Бога. И это одна из причин, по которой его иногда называют числом Богом.

Что же такое такое числа Фибоначчи? Числа Фибоначчи – это последовательность чисел, полученная из суммы двух чисел впереди, например так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т. д.

Например, число 5 получается из суммы двух чисел впереди, а именно 2 + 3.

Может быть, вы тогда спросите, какое отношение эти числа имеют к доказательствам существования Бога?

Это число Фибоначчи показывает некоторые странные факты, но сначала нам нужно узнать о числе Phi? Что такое число Фи?
Наверняка вы знаете, что число Фи – это число 1,618. При чем здесь Фибоначчи? Фи – это результат деления числа в последовательности Фибоначчи на число перед ним.

Чем больше числа Фибоначчи, участвующие в делении, тем ближе результат к 1,618.

Как считалось ранее, это число является свидетельством, указывающим на существование Бога. И считалось священным древними учеными. Считается, что почти все творения Бога имеют в своей жизни числа Фибоначчи, будь то растения, животные или люди. Вот некоторые факты, обнаруженные в природе.

Количество лепестков в цветках

Возможно, большинство людей не обращает особого внимания на количество лепестков на цветке. А при наблюдении оказывается, что количество лепестков на цветке соответствует последовательности Фибоначчи.

Например – количество лепестков 3 (лилии, ирисы), 5 лепестков (лютик), 13 лепестков (календула), 21 лепестков (ромашка, цикорий), 34 лепестка (пиретрум) – количество лепестков 55 (маргаритки)

Цветочные узоры также показывают существование этой последовательности Фибоначчи, например, в подсолнухах.

От центральной точки до внешнего круга узор следует последовательности Фибоначчи.

Человеческое тело

Если вы измерите длину пальца и сравните ее с длиной локтя, вы найдете 1,618.

Попробуйте разделить свой рост на расстояние между пупком и подошвами стоп, результат 1,618.

Сравните длину от плеча до кончиков пальцев с длиной от локтя до кончиков пальцев, результат 1,618.

Сравните длину от талии до ноги с длиной от колена до ноги, результат будет 1,618

Все сравнения размеров человеческого тела – 1,618

Это правда? пожалуйста, докажите это.

Другие факты

И с этим числом связано много других вещей, которые вы можете найти в Google.

Победа Обамы и числовая последовательность Фибоначчи

Эта тема является лишь теорией. Но в июне 2008 года было опубликовано исследование, в то время еще находившихся на стадии предвыборной кампании кандидатов в президенты Обамы и Маккейна. Исследование предполагало и предсказывало, что Обама станет 44-м президентом Америки.

Это исследование основано на политических событиях в Америке, связанных с политической жизнью чернокожих американцев. В том исследовании было заявлено, что на основе ряда лет политических событий в Америке у Обамы есть отличный шанс стать президентом Соединенных Штатов.

Итак, это небольшой обзор чисел Фибоначчи или чисел Бога, которые часто встречаются в природе. Это совпадение? Или это действительно что-то, что было разработано Им, чтобы показать Свое величие? Для тех из вас, кто хочет узнать больше, вы можете выполнить поиск в поисковой системе о Фибоначчи, вы можете получить более полную информацию и некоторые события, связанные с числами Фибоначчи.

Источник

Фибоначчи что это такое простыми словами

Число Фибоначчи. Почему оно так популярно в природе?

Кто такой Фибоначчи?

Последовательность Фибоначчи

Где используется число Фибоначчи

Что такое золотое сечение

Числа Фибоначчи

Описание чисел Фибоначчи

Применение рядов Фибоначчи в информатике и программировании

Последовательность Фибоначчи и генерация псевдослучайных чисел

Числа Фибоначчи в трейдинге

Числа Фибоначчи в визуальном искусстве и дизайне

Заблуждения, связанные с числами Фибоначчи

Последовательность Фибоначчи: что это такое простыми словами, где применяется и как определяется

Как Леонардо Фибоначчи изобрел свою известную последовательность

Что это и для чего нужно

Где используют

Применение в трейдинге

Коррекции Фибоначчи

Дуги Фибоначчи

Веера Фибоначчи

Временные зоны Фибоначчи

Уровни Фибоначчи. Что это и как их использовать в трейдинге

2 обучающих курса

Комментарии

Последние новости

Рекомендованные новости

Числа Фибоначчи — что это и для чего они нужны?

История чисел Фибоначчи

Что такое числа Фибоначчи?

Числа Фибоначчи в трейдинге

1. Коррекции Фибоначчи

2. Дуги Фибоначчи

3. Веера Фибоначчи

4. Временные зоны Фибоначчи

Золотое сечение и числа Фибоначчи

Магия чисел: что такое последовательность Фибоначчи

Александра Смаракова

Леонардо Пизанский: математика и удача

Золотое сечение и спираль Фибоначчи

Числа Фибоначчи в искусстве

Фибоначчи что это такое простыми словами

Фибоначчи

Фибоначчи – кто это?

Последовательность чисел Фибоначчи

«Золотое сечение» (1,618)

Золотое сечение и трейдинг.

Простейший пример

Спираль Фибоначчи

Спираль и ряд чисел Фибоначчи в природе

Последовательность ряда чисел Фибоначчи, «золотое сечение» и Спираль Фибоначчи в архитектуре

Подводя итоги

Фибоначчи повсюду!

Числа Фибоначчи и золотое сечение

Почему эта последовательность настолько уникальна

Числа Фибоначчи в природе

Числа Фибоначчи в теле человека

Числа Фибоначчи в биржевой торговле

Числа Фибоначчи в фотографии и искусстве

Божественная гармония: что такое золотое сечение простыми словами. Тайны мироздания в числах

Что такое золотое сечение?

Золотое сечение в математике

Тайна «числа бога»

Последовательность Фибоначчи

Количество лепестков в цветках

Человеческое тело

Другие факты

Победа Обамы и числовая последовательность Фибоначчи

Вам также понравится

если открываешь ип впервые надо ли платить налоги

заключение договора на вывоз тбо для юридических лиц

какие документы надо для заключения договора на газ

Добавить комментарий Отменить ответ